数理最適化問題のチートシート的なもの (4) - 半正定値計画・2次錐計画の続きです。
今回は組合せ最適化を一気に扱います。とりあえずこれで終了です。
6. 組合せ最適化問題の複雑さ・難しさ
さまざまな問題に対して、効率的なアルゴリズムの存否や問題の難易度の意味といった観点から、問題の難しさや複雑さを研究するのが計算複雑性理論。
6.1 アルゴリズムの計算量
- 時間計算量:アルゴリズムが停止するまでに必要な四則演算などの基本操作の実行回数を表す。
- 空間計算量:アルゴリズムが停止するまでに必要なメモリ量を表す。
6.2 計算量とアルゴリズムの分類
- 多項式時間アルゴリズム:計算量が多項式で書ける場合。
- 指数時間アルゴリズム:計算量が多項式関数では抑えられない場合。
6.3 計算の複雑さと問題の難しさ
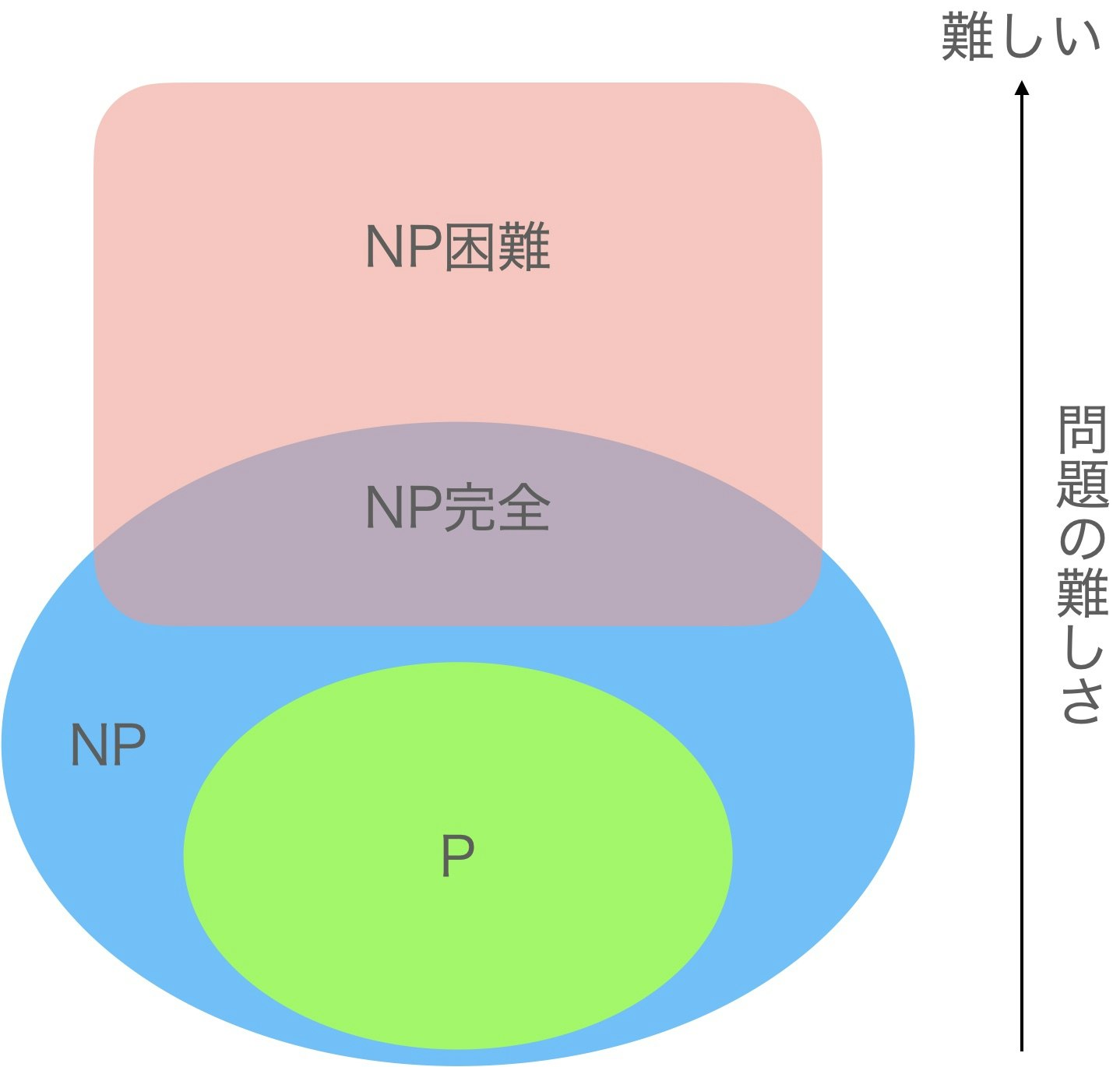
- クラス $P$:決定性のコンピュータ (分岐を並列に同時に実行可能なコンピュータ) で多項式時間で解ける問題の集合。
- クラス $NP$:非決定性のコンピュータ (分岐を並列に同時に実行可能なコンピュータ) で多項式時間で解ける問題の集合。
- $NP$ 困難:クラス $NP$ に含まれる任意の問題と難しさが同等かそれ以上の問題の集合。
- $NP$ 完全:クラス $NP$ に属する問題のうち、$NP$ 困難な問題クラス。
これらの複雑性クラスについて以下のような話題がある。
- $P\subseteq NP$ である。
- $P\neq NP$ であるかは分かっていない ($P\neq NP$ 予想)。
- $NP$ 困難な問題に対して、多項式時間アルゴリズムが存在しないことは証明されていない。
6.4 複雑性クラスと組合せ最適化問題
各組合せ最適化問題の複雑性クラスは以下。
- クラス $P$:オイラー閉路問題、最短路問題、最大流問題、最小費用流問題、最小全域木問題、割当問題、2-SAT、最大マッチング問題、最大重みマッチング問題、最大重み最大マッチング問題
- $NP$ 困難:整数最適化問題、巡回セールスマン問題、最大安定集合問題、集合分割問題、ナップザック問題、ビンパッキング問題、最大クリーク問題、最小頂点被覆問題、最小極大マッチング問題
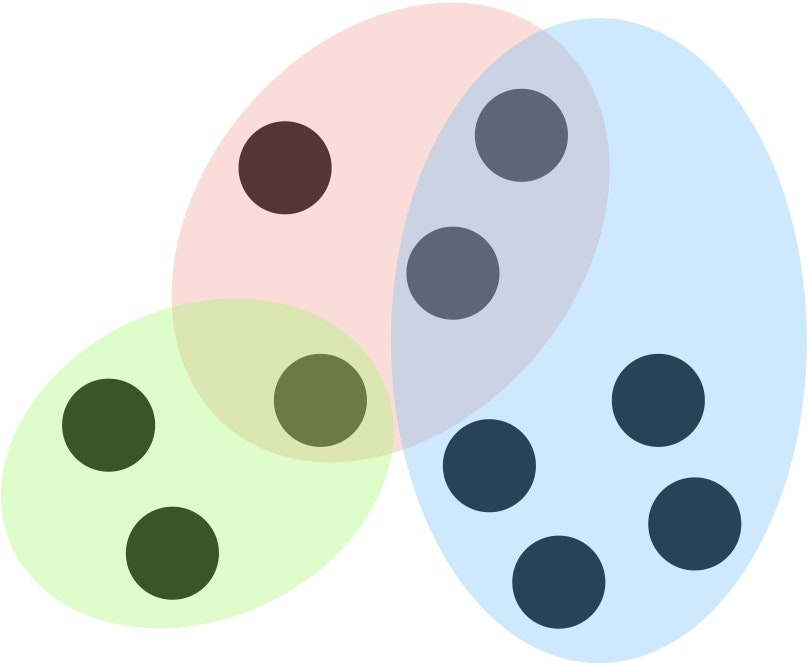
7. 組合せ最適化問題の全体像
以下の図のように整理される。

8. 組合せ最適化の標準問題
8.1 グラフ問題・ネットワーク問題
8.1.1 最小全域木問題
問題
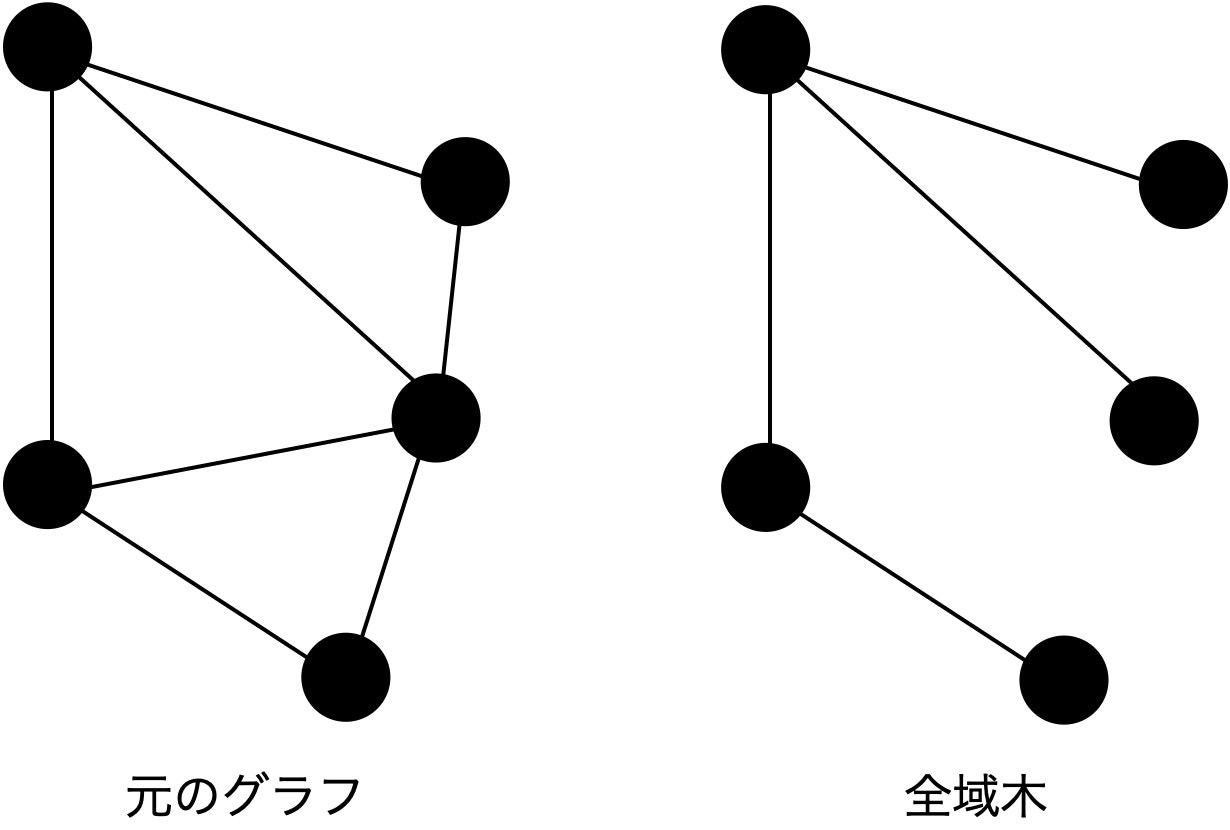
最小全域木とは、当該グラフの全ノードを含む部分グラフのうち、連結で閉路を持たないグラフ (=木) のこと。
無向グラフ $G=(V, E)$ 上の辺 $e$ の重みを $w(e)$ とするとき、全域木 $T=(V, E_T)$ 上の辺の重みの総和 $\displaystyle\sum_{e\in E_T}w(e)$ を最小にする全域木を求める問題。
定式化は以下。$\delta (S)$ は、$S\subset V$ に一方の端点、$V\setminus S$ にもう一方の端点を持つ辺全体の集合。
\begin{array}
&\min &\displaystyle\sum_{e\in E}w(e)x_e \\
s.t. &\displaystyle\sum_{e\in C}x_e\leq |C|-1 &\forall C: \rm{closed~path~of}~G \\
&\displaystyle\sum_{e\in\delta (S)}x_e\geq 1 &\forall S\subset V,~S\neq\emptyset,~S\neq V \\
&x_e\in\lbrace 0,1\rbrace &\forall e\in E
\end{array}
制約条件は、木であることの必要十分条件。定式化にはいくつかバリエーションがある。
データのクラスター分析やネットワークの設計に使われる。
解法
クラスカル法やプリム法などの貪欲法ベースの多項式時間アルゴリズムがある。
クラスカル法は以下。if文の判定には、Union-Find木を使うと効率的。計算量は $O(|E|\log |V|)$。
T ← 空グラフ
E ← すべての辺の集合
while (E が空でない)
e ← 重みが最小の辺
E から e を削除する
if (e の端点のうち少ないとも一方が T に含まれない)
T ← T + e
end if
end while
プリム法は以下。重み最小のエッジ選択にはヒープを使うと速い。計算量はヒープを使う場合で $O(|E|\log |V|)$。
T ← 適当に選んだノード1つのみの集合
V ← すべての頂点の集合
while (V が空でない)
e ← T に含まれるノードを始点、含まれないノードを終点とするエッジのうち、重み最小のもの
E から e を削除する
T ← T + e
end while
8.1.2 最大カット問題
問題
カットとは、無向グラフ $G=(V,E)$ において、$V$ を2つの部分集合 $V_1, V_2$ に分割する組合せのこと。
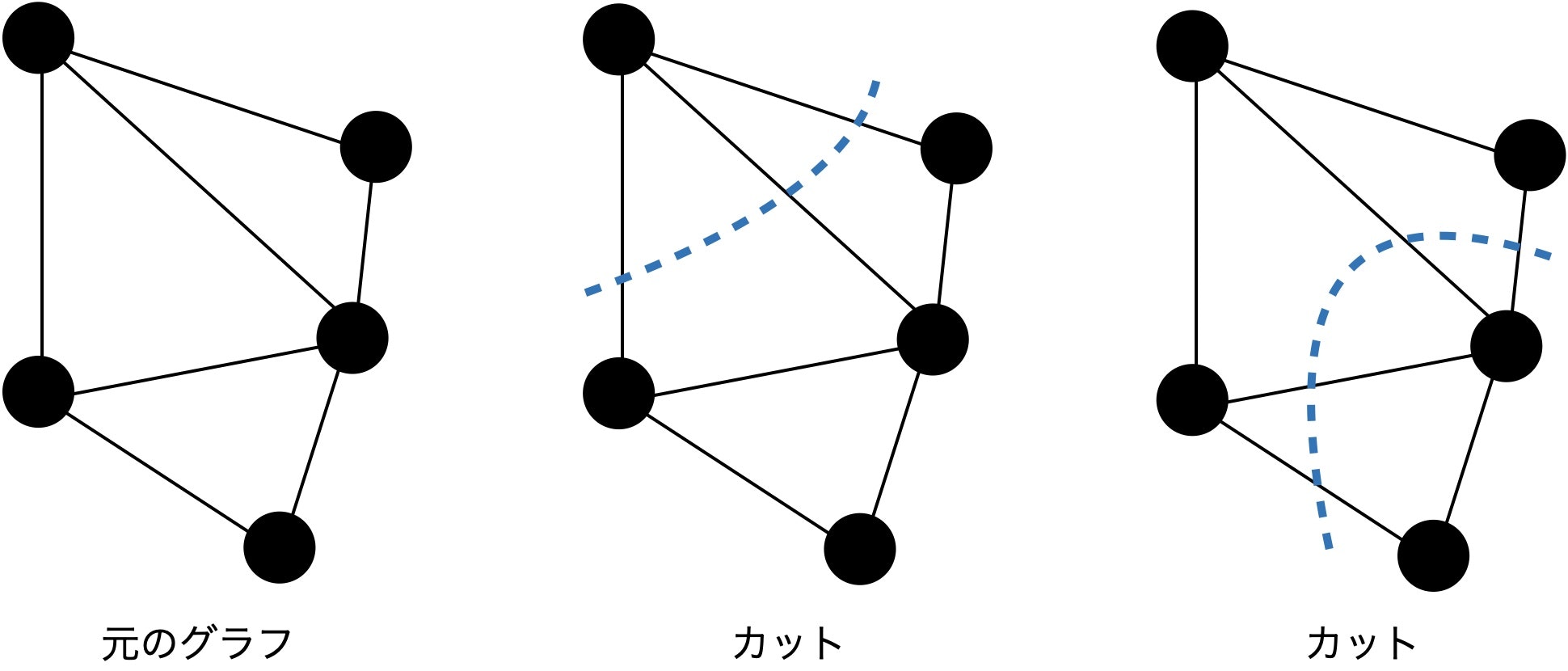
無向グラフ $G=(V,E)$ において、$\displaystyle\sum_{v_i\in V_1, v_j\in V_2, i<j}w_{ij}$ を最大にするカット $V_1, V_2$ を求める問題。
定式化は以下。$u_i\in\lbrace -1,1\rbrace$ は、ノード $i$ が $V_1$ に属する場合 $+1$、$V_2$ に属する場合 $-1$ を割り当てる。
\begin{array}
&\max &\displaystyle\frac{1}{2}\sum_{v_i\in V_1,v_j\in V_2, i<j}w_{ij}(1-u_iu_j) \\
s.t. &u_i\in\lbrace -1,1\rbrace &\forall v_i\in V
\end{array}
ネットワーク監視の効率化などに用いられる。より複雑な組合せ最適化問題の部分問題として用いられることも多い。
解法
NP完全。メタヒューで解く。多項式時間アルゴリズムは存在しないと考えられている。
なお、最小カット問題には多項式時間アルゴリズムが存在する。最小カット問題は最大流問題の双対問題。
8.1.3 最小頂点被覆問題
問題
頂点被覆とは、頂点の集合 $C\subseteq V$ であり、任意のエッジについて少なくとも一方の端点が $C$ に含まれるもの。
頂点被覆 $C$ のうち要素数 $|C|$ が最小のものを求める問題。
重みつきの場合の定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{v_i\in V}w(v_i)x_i \\
s.t. &x_i+x_j\geq 1 &\forall e_{ij}=(v_i,v_j)\in E \\
&x_i\in\lbrace 0,1\rbrace &\forall v_i\in V
\end{array}
配置計画 (交差点への警備員の配置など) に用いられることが多い。より複雑な組合せ最適化問題の部分問題として用いられることも多い。
解法
NP困難。メタヒューを使うことが多い。
8.1.4 最大安定集合問題
問題
安定集合 (独立集合) とは、ノード集合 $S\subseteq V$ で $S$ の任意の2つのノードをつなぐエッジが存在しない集合のこと。
安定集合 $S$ のうち要素数 $|S|$ が最大のものを求める問題。
\begin{array}
&\max &\displaystyle\sum_{v_i\in V}x_i \\
s.t. &x_i+x_j\leq 1 &\forall e_{ij}=(v_i,v_j)\in E \\
&x_i\in\lbrace 0,1\rbrace &\forall v_i\in V
\end{array}
より複雑な組合せ最適化問題の部分問題としてしばしば用いられる。
解法
NP困難。メタヒューを使う。
8.1.5 最短路問題
問題
あるノード $v_s\in V$ から別のノード $v_t \in V$ への経路の中で最もコストの小さいものを求める問題。
エッジ $e_{ij}$ の重みを $a_{ij}$ として、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{e_{ij}\in E}a_{ij}x_{ij} \\
s.t. &\displaystyle\sum_{v_j\in V}x_{ij}-\sum_{v_k\in V}x_{ki}=\left\{
\begin{array}
~1 &i=s \\
-1 &i=t \\
0 &\rm{otherwise}
\end{array} \right. \\
&x_{ij}\in\lbrace 0,1\rbrace &e_{ij}\in E
\end{array}
鉄道の経路案内や車のナビに応用されている。
解法
単一始点最短路問題の解法は、コストが非負の場合ダイクストラ法、負のコストも許す場合ベルマン・フォード法。全点対最短路問題はワーシャル・フロイド法。
ダイクストラ法は以下。d[u] が最小となるノードの取り出しは Q にヒープを使うと効率的。計算量は $O((|E|+|V|)\log |V|)$。
すべての v について d[v] ← ∞
d[v_s] ← 0
Q ← すべての頂点の集合
while (Q が空でない)
u ← Q のうち d[u] が最小となるノード
Q から u を削除する
for each (u を始点とする辺の終点 v)
if d[v] > d[u] + cost[u, v]
d[v] ← d[u] + cost[u, v]
end if
end for
end while
ベルマン・フォード法は以下。計算量は $O(|V||E|)$。
すべての v について d[v] ← ∞
d[v_s] ← 0
for i = 1 to |V|
for each (u, v) in V
if d[v] > d[u] + cost[u, v]
d[v] = d[u] + cost[u, v]
end if
end for
end for
ワーシャル・フロイド法は以下。計算量は $O(V^3)$。
d[i, j] ← 辺 (i, j) が存在すれば cost[i, j]、存在しなければ ∞
for each k = 1 to |V|
for each i = 1 to |V|
for each j = 1 to |V|
if d[i, j] > d[i, k] + d[k, j]
d[i, j] = d[i, k] + d[k, j]
end if
end for
end for
end for
8.1.6 最大流問題
問題
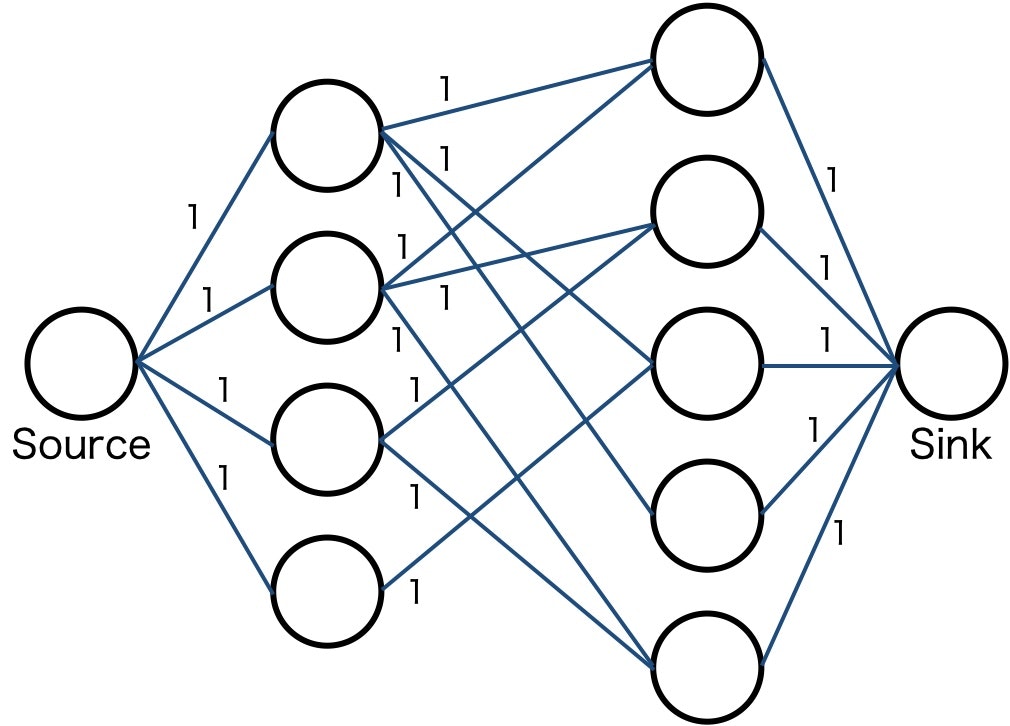
容量付きのリンクから構成される有向グラフにおいて、ソースノードからシンクノードへの総流量が最大となるようなフローを求める問題。
フロー $\boldsymbol{x}$ のノード $v_i$ における超過 $f_{\boldsymbol{x}}(v_i)$ を以下のように定義する。
\displaystyle f_{\boldsymbol{x}}(v_i)=\sum_{(j,i)\in E}x_{ji}-\sum_{(i,j)\in E}x_{ij}
ソースノード $v_s$、シンクノード $v_t$、リンク $(i,j)$ の容量を $u_{ij}$ として、定式化は以下。1つ目の制約が流量保存則、2つ目の制約が容量制約。
\begin{array}
&\max &f_{\boldsymbol{x}}(v_t) \\
s.t. &f_{\boldsymbol{x}}(v_i)=0 &\forall v_i\in V\setminus\lbrace v_s,v_t\rbrace \\
&0\leq x_{ij}\leq u_{ij} &\forall e_{ij}\in E
\end{array}
水や道路交通の流れに関する問題に適用されたり、スケジューリングや分子生物学に応用されている。
解法
線形最適化問題なので単体法で解ける。
最大流問題では特に、フォード・ファルカーソン法 (フロー増加法) という効率的なアルゴリズムがある。「各リンクにフローをどれだけ追加でき、どれだけ減らすことができるか」を表す残余ネットワークという概念を導入する。
全ての e ∈ E について f[e] ← 0
while (残余ネットワークにおいてソースノードからシンクノードへのパス p が存在)
q ← パス p に含まれるエッジのうちの最小容量
パス p にフロー q を流す
end while
8.1.7 最小費用流問題
問題
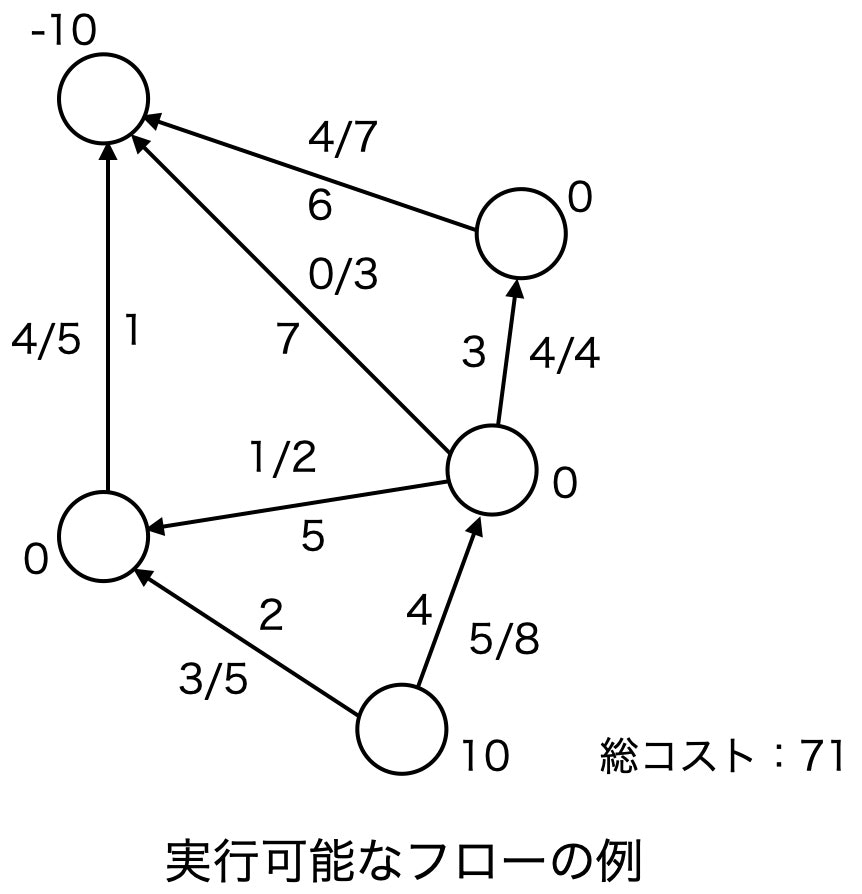
有向グラフ $G=(V, E)$ において、各エッジの要領とコスト、ノードの需給量が与えられたとき、各エッジの容量を超過せず各ノードの流出量が需給量と等しくなるフローの中で、各エッジの流量に対するコストの総和が最小となるフローを求める問題。
\begin{array}
&\min &\displaystyle\sum_{(i,j)\in E}c_{ij}x_{ij} \\
s.t. &f_{\boldsymbol{x}}(v_i)=b_i &\forall v_i\in V \\
&0\leq x_{ij}\leq u_{ij} &(i,j)\in E
\end{array}
解法
- ネットワーク単体法。単体法における基底解をエッジの集合に置き換える ($x_{ij}=1$ のとき、エッジ $(i,j)$ が有効) と全域木となり、また、全域木に対して需給制約を満たすフローは一意に定まるため、基底解と全域木は一対一対応する。そのため、単体法において実行可能基底解を順々に探索するのと同様に、全域木を次々に探索するという発想。新しい全域木 (=実行可能基底解) を求める際は、需給制約を満たしつつ新たなエッジに $\theta$ だけ流して閉路を発生させたときに、最初に流量が負となるエッジを取り除けばよい。
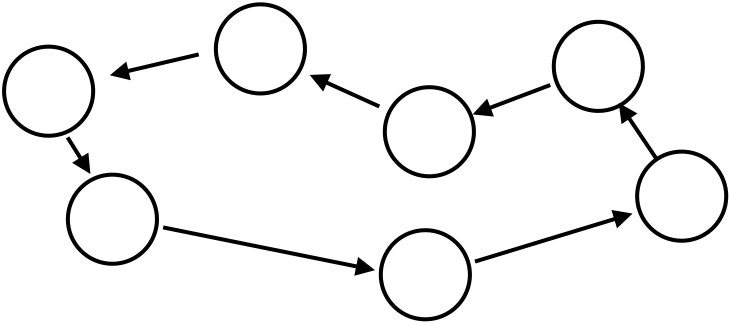
- 負閉路除去法。残余ネットワークにおいて、元のエッジと逆向きのエッジのコストを、元のエッジのコストの-1倍とする。
f[e] ← フロー保存条件を満たすフロー
while (負の閉路が存在)
f[e] ← 負の閉路に流せるだけ流したときのフロー
end while
8.2 経路問題
8.2.1 運搬経路問題 (Vehicle Routing Problem, VRP)
問題
デポから出発し、いくつかのノードを訪問してデポに戻るルートを最適化する。需要量や移動コスト、最大稼働時間などの制約のもとで解く。バリエーションがいくつかある。
例えば、以下の問題。
顧客の集合 $V=\lbrace 0,\cdots,n\rbrace$ と運搬車の集合 $M=\lbrace 1,\cdots,M\rbrace$ が与えられたとする。各運搬車はデポ $0$ を出発して割り当てられた顧客集合をめぐり配送を行い、デポ $0$ に戻る。各顧客 $i\in V$ についてサービスの需要量は $a_i$、各運搬車 $k\in M$ の最大積載量は $u$ であり、顧客 $i, j$ 間の移動コストが $c_{ij}$ であるとする。各顧客の需要は1台の運搬車の1度の訪問で満たされる。このとき、総移動コストが最大となるように全ての運搬車のルートを求めよ。
$x_{ij}^k$ は運搬車 $k$ が顧客 $i$ から $j$ へ進むか否かのバイナリ変数、$w_i^k$ は運搬車 $k$ が顧客 $i$ までに訪問した顧客の需要量の総和として、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{(i,j)\in E}c_{ij}\sum_{k\in M}x_{ij}^k \\
s.t. &\displaystyle\sum_{j\in\lbrace j|(0,j)\in E\rbrace} x_{0j}^k=1 &\forall k\in M \\
&\displaystyle\sum_{j\in\lbrace j|(i,j)\in E\rbrace}x_{ij}^k=\sum_{j\in\lbrace j|(j,i)\in E}x_{ji}^k &\forall i\in V, \forall k\in M \\
&w_j^k\geq a_j-u\left( 1-x_{ij}^k\right) &\forall (i,j)\in E, i=0, \forall k\in M \\
&w_j^k\geq w_i^k+a_j-u\left( 1-x_{ij}^k\right) &\forall (i,j)\in E, i\neq 0, \forall k\in M \\
&w_i^k\leq u &\forall i\in V, \forall k\in M \\
&\displaystyle\sum_{j\in\lbrace j|(i,j)\in E\rbrace}\sum_{k\in M}x_{ij}^k=1 &\forall i\in V, i\neq 0 \\
&x_{ij}^k \in \lbrace 0,1\rbrace &\forall (i,j)\in E,\forall k\in M \\
&w_i^k\geq 0 &\forall i\in V, \forall k\in M
\end{array}
店舗への配送、郵便などの配達、ごみ収集、航空機の路線決定など幅広い問題をカバーしている。
解法
バリエーションのほとんどはNP困難のため、近似解法やメタヒュー。集合被覆問題として定義されることもある。
8.2.2 巡回セールスマン問題 (Traveling Salesman Problem, TSP)
問題
すべてのエッジを1回ずつ通り最初のエッジに戻るルートのうち、総コストが最小となるルートを求める問題。
定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{(i,j)\in E}c_{ij}x_{ij} \\
s.t. &\displaystyle\sum_{j=1}^{n}x_{ij}=1 &\forall i \in V \\
&\displaystyle\sum_{i=1}^{n}x_{ij}=1 &\forall j\in V \\
&\displaystyle\sum_{(i,j)\in\delta (S)}x_{ij}\geq 1 &\forall S\subset V,S\neq\emptyset,S\neq V \\
&x_{ij}\in\lbrace 0,1\rbrace &i,j\in V, i\neq j
\end{array}
配送計画問題やプリント基板へのドリル穴開け、VLCIの設計などに用いられる。
解法
NP困難。近似解法が多く開発されている。bit DPで計算量を $O(n!)$ から $O(n^22^n)$ までは落とせる。
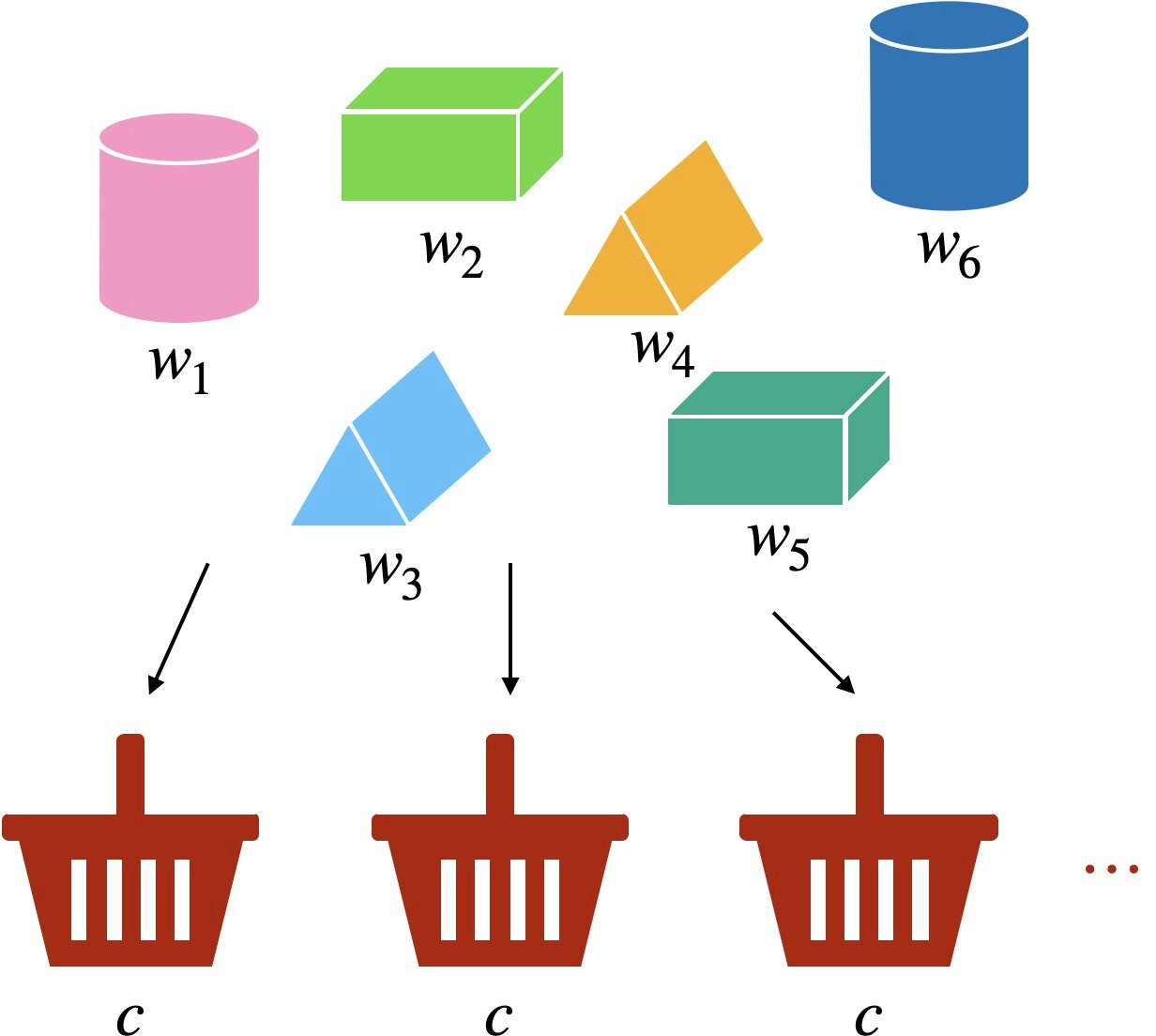
8.3 集合被覆問題 (Set Covering Problem, SCP)
8.3.1 集合被覆・分割問題
問題
いくつかの要素からなる集合 $M$ と $M$ の部分集合族が与えられ、各部分集合にはコストが与えられているとする。
$M$ のすべての要素をカバーするようにいくつかの部分集合を選び、選んだ部分集合のコストの総和を最小にするのが集合被覆問題。
選ばれた部分集合が互いに重ならないという条件を課す場合が集合分割問題。
より具体的に数式に落とすと以下。集合 $M=\lbrace 1,\cdots,m\rbrace$ の $n$ 個の部分集合 $S_j \subseteq M$、$j\in N=\lbrace 1,\cdots,N\rbrace$ を考える。このとき、以下の条件を満たす集合の族 $\lbrace S_j~|~j\in X\rbrace$ を集合 $M$ の被覆という。
\bigcup_{j\in X}S_j=M
集合 $M$ の被覆で、さらに $S_j\cap S_k=\emptyset,~j,k\in X,~j\neq k$ が成り立つ場合、集合 $M$ の分割という。
集合被覆問題の定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{j=1}^{n}c_jx_j \\
s.t. &\displaystyle\sum_{j=1}^{n}a_{ij}x_j\geq 1 &\forall i\in M \\
&x_j\in\lbrace 0,1\rbrace &\forall j\in N
\end{array}
集合分割問題の定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{j=1}^{n}c_jx_j \\
s.t. &\displaystyle\sum_{j=1}^{n}a_{ij}x_j=1 &\forall i\in M \\
&x_j\in\lbrace 0,1\rbrace &\forall j\in N
\end{array}
運搬経路問題、スケジューリング問題、施設配置問題、割当問題など、別の標準問題に応用される。集合被覆問題は組合せ最適化問題において重要な基本的な問題構造であると言える。
解法
NP困難。線形緩和やラグランジュ緩和を利用した効率的な手法が提案されている。
8.4 スケジューリング問題
ジョブを様々な制約のもとで実行しなくてはならないとき、実行可能なスケジュールや最適化スケジュールを求める問題。
8.4.1 ジョブショップ問題
問題
ジョブショップとは、機械加工工場などで同種の機能や性能を持つ機械設備をグループ化して編成した機能別配置工程のこと。
ジョブショップ問題とは、ジョブごとに指定された順序で順次処理されるジョブショップにおいて、目的関数を最適にするよう書く機械におけるジョブの処理順序を決定する問題。例えば1機械問題など以下のように記述される。
与えられた $n$ 個のジョブ $V=\lbrace 1,\cdots,n\rbrace$ を1台の機械で処理するとする。各ジョブ $i$ の処理時間は $p_i$ である。機械は1度に1つのジョブしか処理できず、あるジョブの処理中は他のジョブは処理できない。また、各ジョブ $i$ には、準備時間 $r_i$ と納期 $d_i$ が与えられている。このとき、目的関数 $f$ を最小にするジョブの順列を求めよ。

$x_{ij}$ をジョブ $i$ がジョブ $j$ より先に処理されるかを表すバイナリ変数、$M$ を十分大きな数とし、定式化は以下。
\begin{array}
&\min &f \\
s.t. &c_i\geq r_i+p_i &\forall i\in V \\
&c_i\geq c_j+p_j-Mx_{ij} &\forall i,j\in V,i<j \\
&c_i\leq c_j-p_i+M(1-x_{ij}) &\forall i,j\in V,i<j \\
&c_i<d_i
\end{array}
問題のバリエーションとして、以下などがある。
- 並列機械問題:2台以上の機械で各ジョブはいずれか1台で1度だけ処理されるとき、各ジョブに対する機械の割当と各機械に割当てられたジョブの処理順序を決定する問題。
- フローショップ問題:工程順序がどのジョブについても同じ場合の問題。
- オープンショップ問題:ジョブの一部またはすべての工程順序が任意で、工程順序も最適化の対象となる場合の問題。
解法
多くのスケジューリング問題はNP困難だが、工夫された分枝限定法を持ち言えることでかなりジョブ数が大きい問題も解ける場合がある。
また、2機械の機械問題はジョンソン法という貪欲法ベースの効率的な厳密解法がある。ただし、各ジョブの準備時間と納期が全て同一であること、各ジョブには前工程と後工程の2つの処理が含まれることが条件。
while (未決定の処理が存在)
p ← 未決定かつ処理時間が最小の処理
if (p が前工程)
当該ジョブをスケジュールの最初から順に並べる
else if (p が後工程)
当該ジョブをスケジュールの後ろから順に並べる
end if
当該ジョブの各処理を決定済みとする
end while
8.4.2 勤務スケジューリング問題
問題
工場の従業員、交通機関の乗務員、病院の看護師など様々な職場におけるある期間内の勤務スケジュールを作成する問題。
看護師スケジューリング問題や乗務員スケジューリング問題など様々なバリエーションがある。例えば看護師スケジューリング問題は、以下のような条件のもとでシフトを決定する問題。
- 拘束条件1:毎日の各勤務に必要な人数確保
- 拘束条件2:スキルレベルや所属チームを考慮した各シフトの人員構成
- 拘束条件3:各看護師の勤務回数を決められた範囲内に収める
- 拘束条件4:その他の業務や休みの希望の充足
- 拘束条件5:禁止されているシフトパターンの排除
すべての制約を満たすのは難しいため、必ず守る必要のある制約は絶対制約とし、それ以外はソフト制約とすることも多い。
解法
大規模な整数計画問題なので、厳密解法は厳しい。メタヒューを適用する研究が盛ん。
8.5 切出し・詰込み問題
- 切出し問題:定型の母材から必要とされる形状や大きさの資材を切出し、母材の材料費や切出しにかかる工程費を最小化する問題
- 詰込み問題:与えられた図形をある容器の中に図形の重複がないように配置する問題
本質的には、いくつかの対象物を互いに重ならないように与えられた領域内に効率よく配置する問題。
8.5.1 ナップサック問題
問題
容量 $c$ のナップサックと $n$ 個の荷物 $N=\lbrace 1,\cdots,n\rbrace$ が与えられており、荷物 $i\in N$ の容量を $w_i$、価値を $p_i$ とするとき、容量制限 $c$ の範囲で価値の和が最大になる荷物の詰合せを求める問題。
$x_i$ を荷物 $i$ がナップサックに入っているかを表すバイナリ変数とすると、定式化は以下。
\begin{array}
&\max &\displaystyle\sum_{i=1}^{n}p_ix_i \\
s.t. &\displaystyle\sum_{i=1}^{n}w_ix_i\leq c \\
&x_i\in\lbrace 0,1\rbrace &\forall i\in N
\end{array}
解法
NP困難。厳密解法では分枝限定法や動的計画法、近似解法では局所探索法などが用いられる。動的計画法は以下。「$i$ 個目までの品物までで、ナップサックの容量が $j$ のときの最適値」をDPテーブルとする。
dp ← (N+1)×(c+1)の配列
for each j = 0 to c
dp[0][j] = 0
end for
for each i = 1 to N
for each j = 0 to c
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w_i] + p_a)
end for
end for
PRINT dp[N][C]
8.5.2 ビンパッキング問題
問題
容量 $c$ の箱と $n$ 個の荷物 $N=\lbrace 1,\cdots,n\rbrace$ が与えられており、荷物 $j\in N$ の容量を $w_j$ とするとき、すべての荷物を詰合せるのに必要な箱の数を最小にする詰合せを求める問題。
$x_{ij}$ を箱 $i$ に荷物 $j$ が入っているかのバイナリ変数、$y_i$ を箱 $i$ が使われているかのバイナリ変数とすると、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{i=1}^n y_i \\
s.t. &\displaystyle\sum_{j=1}^n w_jx_{ij}\leq cy_i &\forall i\in N \\
&\displaystyle\sum_{i=1}^n x_{ij} = 1 &\forall j \in N \\
&y_i\in\lbrace 0,1\rbrace &\forall i\in N \\
&x_{ij}\in\lbrace 0,1\rbrace &\forall i\in N, j\in N
\end{array}
解法
NP困難。分枝限定法や貪欲法・列生成法をはじめとする近似解法が用いられる。
8.5.3 その他
以下のような問題がある。
- 1次元資材切出し問題:母材から様々な大きさ位の必要とされる量の資材を切出すときに使用する母材を最小にする問題。
- 長方形詰込み問題:様々な大きさの長方形を2次元平面のある領域内に重なりのないように配置する問題。
8.6 配置問題
施設配置問題とは、施設の配置可能な候補点と施設に割当たる対象を与件とし、ある基準を満たす施設の配置を決定する問題。以下は施設配置問題の例。
- メディアン問題:顧客から最も近い施設への距離の総和を最小化するように施設を配置する問題。
- センター問題:顧客から最も近い施設への距離の最大値を最小化するように施設を配置する問題。
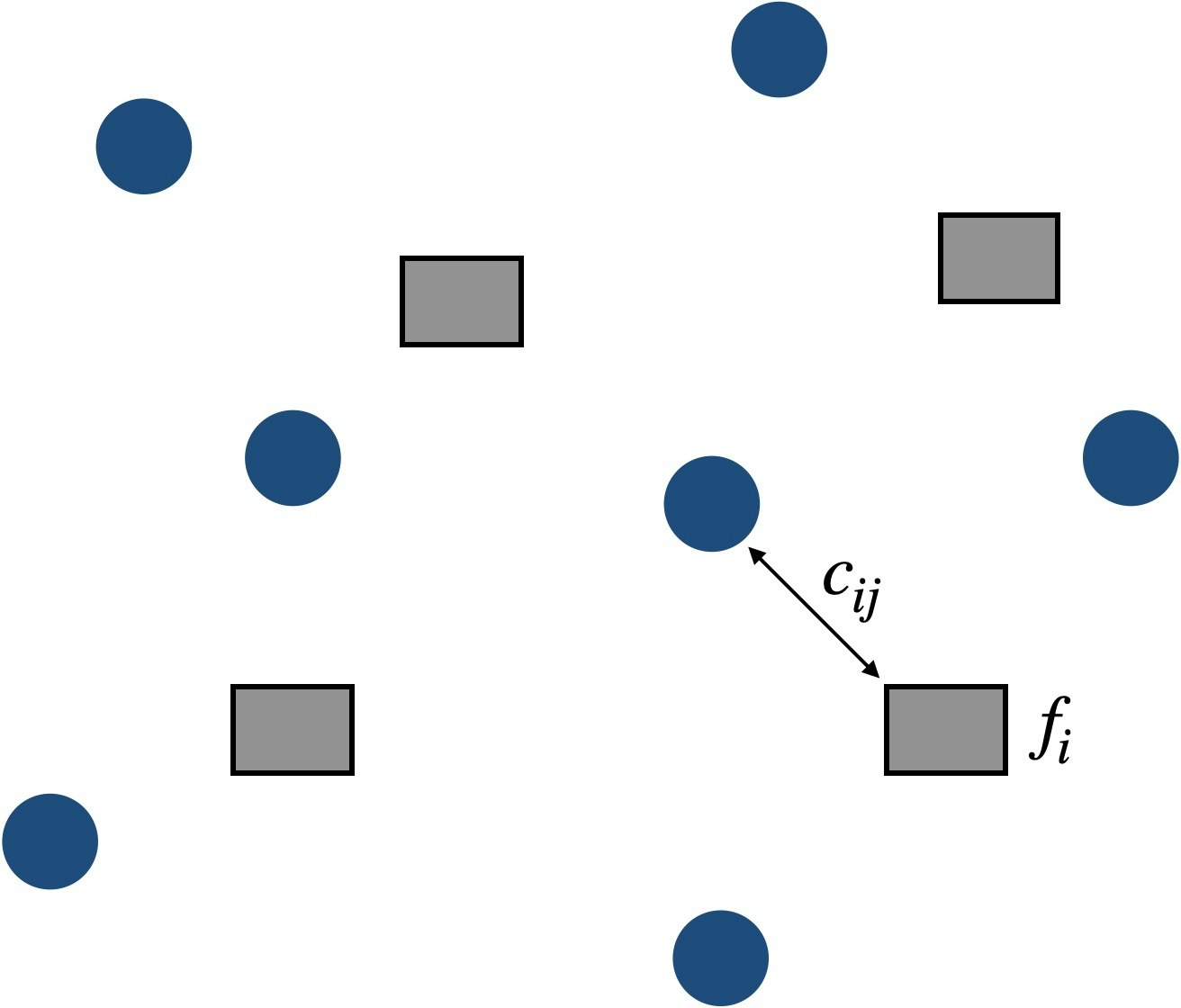
8.6.1 容量制約なし施設配置問題
問題
顧客の集合 $D$ と施設の配置可能地点の集合 $F$ が与えられ、各施設 $i\in F$ を開設するための固定コストを $f_i$、各顧客 $j\in D$ と各施設 $i$ の間の単位需要当たりの輸送コストを $c_{ij}$ とするとき、施設開設固定コストと輸送コストの総和が最小となるように、開設する施設を選択する問題。
$x_{ij}$ を施設 $i$ によって顧客 $j$ の需要が満たされる割合、$y_i$ を施設 $i$ を開設するか否かのバイナリ変数として、定式化は以下。MIPになる。
\begin{array}
&\min &\displaystyle\sum_{i\in F}f_iy_i+\sum_{i\in F}\sum_{j\in D}c_{ij}x_{ij} \\
s.t. &x_{ij}\leq y_i &\forall i\in F, j\in D \\
&\displaystyle\sum_{i\in F}x_{ij}=1 &\forall j\in D \\
&x_{ij}\geq 0 &\forall i\in F, j\in D \\
&y_i\in\lbrace 0,1\rbrace &\forall i\in F
\end{array}
解法
施設配置問題の多くはNP困難。緩和手法や近似手法が用いられる。
8.7 割当問題・マッチング問題
ある集合の各要素についてそれぞれ別の集合のどの要素に割当てると、さまざまな制約条件を満たしつつ、最もよい割当を行うことができるのかを決定する問題。
8.7.1 2次割当問題
問題
対象物と同数の割当先が与えられているとき、割当先間の輸送量と距離の席の総和を最小化する問題。
より具体的には、対象物 $P=\lbrace P_1,\cdots,P_n\rbrace$ の割当先 $L=\lbrace L_1,\cdots,L_n\rbrace$ を考え、対象物 $P_i$ と $P_j$ の間の輸送量 $q_{ij}$ と割当先 $L_k$ と $L_l$ の間の距離 $d_{kl}$ が与えられているとき、輸送量と距離の積の総和を最小にする割当を求める問題。
$x_{ij}$ を対象物 $P_i$ が割当先 $L_j$ に位置するか否かのバイナリ変数とし、以下のように定式化される。
\begin{array}
&\min &\displaystyle\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{k=1}^{n}\sum_{l=1}^{n}q_{ij}d_{kl}x_{ik}x_{jl} \\
s.t. &\displaystyle\sum_{j=1}^{n}x_{ij}=1 &\forall i\in V \\
&\displaystyle\sum_{i=j}^{n}x_{ij}=1 &\forall j\in V \\
&x_{ij}\in\lbrace 0,1\rbrace &\forall i,j\in V
\end{array}
工場内の機械の配置や外部記憶装置上でのデータ配列などの用途がある。
解法
NP困難。巡回セールスマン問題と同じく、目的関数を最小にする順列を求める問題だが、目的関数が2次で難しい。分枝限定法やメタヒュー。
8.7.2 一般化割当問題
問題
与えられたいくつかの仕事をエージェントに割当てるとき、割当に伴うコストの総和を最小化する問題。例えば以下。
$n$ 個の仕事 $J=\lbrace 1,\cdots,n\rbrace$ と $m$ 人のエージェント $I=\lbrace 1,\cdots,m\rbrace$ に対して、仕事 $j\in J$ をエージェント $i\in I$ に割当てたときのコスト $c_{ij}$ と資源の要求量 $a_{ij}$、および各エージェント $i\in I$ の利用可能資源量 $b_i$ が与えられている。
それぞれの仕事を必ずいずれか1つのエージェントに割当なければならず、また、各エージェントに割当てられた仕事の総資源要求量が、そのエージェントの利用可能資源量を超えないようにしなくてはならない。このとき、割当に伴うコストの総和を最小化するような割当を求めよ。
$x_{ij}$ を仕事 $j$ をエージェント $i$ に割当てるか否かのバイナリ変数として、定式化は以下。
\begin{array}
&\min &\displaystyle\sum_{i\in I}\sum_{j\in J}c_{ij}x_{ij} \\
s.t. &\displaystyle\sum_{j\in J}a_{ij}x_{ij}\leq b_i &\forall i\in I \\
&\displaystyle\sum_{i\in I}x_{ij}=1 &\forall j\in J \\
&x_{ij}\in\lbrace 0,1\rbrace &\forall i\in I,j\in J
\end{array}
解法
実行可能解が存在するかの判定問題がNP完全。一部の制約を緩和して実行不可能解も探索の対象とする方法が有効。
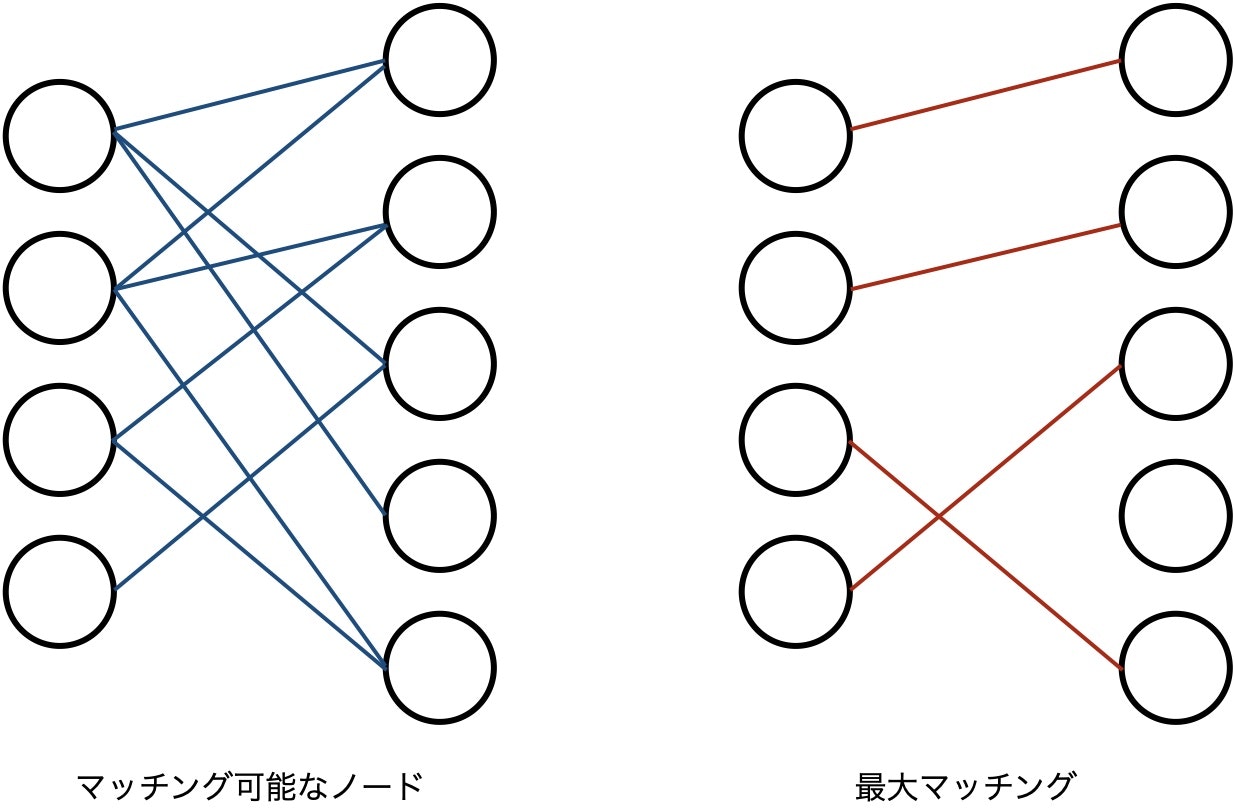
8.7.3 最大マッチング問題
問題
無向グラフ $G=(V,E)$ に対してエッジの本数が最大のマッチングを求める問題。
$A$ を接続行列、$\boldsymbol{x}$ とエッジが存在するか否かのバイナリ変数のベクトルとして、定式化は以下。
\begin{array}
&\max &\boldsymbol{1}^T\cdot\boldsymbol{x} \\
s.t. &A\boldsymbol{x}\leq\boldsymbol{1} \\
&x(e)\in\lbrace 0,1\rbrace &\forall e\in E
\end{array}
仕事の割当や学生と授業の割り当て、人員の配属割当などに用いられる。
解法
2部グラフの場合、片方のグラフに仮想的なソースノード、もう片方のグラフに仮想的なシンクノードを定義して繋ぎ、すべてのエッジの容量を1として最大流問題を考えればよい。
一般のグラフの場合はエドモンズ法 (まだ理解できていないので、理解したら追記します)。
8.7.4 最大重みマッチング問題
問題
各辺 $e\in E$ の重み $w(e)$ が与えられている無向グラフ $G=(V,E)$ に対し、重みの和 $\displaystyle\sum_{e\in M}$ が最大のマッチング $M$ を求める問題。
$\delta(v)$ をノード $v$ に接続しているエッジ集合、$x(e)$ をエッジ $e$ がマッチング $M$ の要素か否かのバイナリ変数として、定式化は以下。
\begin{array}
&\max &\displaystyle\sum_{e\in E}w(e)x(e) \\
s.t. &\displaystyle\sum_{e\in\delta(v)}x(e)\leq 1 &\forall v\in V \\
&x(e)\in\lbrace 0,1\rbrace &\forall e\in E
\end{array}
解法
2部グラフではハンガリー法。一般グラフではエドモンズ法。最大重み完全マッチングの場合のハンガリー法は以下。
for each element in A
element ← max_element - element
end for
for each row in A
element ← element - min_element_in_row
end for
for each col in A
element ← element - min_element_in_col
end for
while 値が0の成分のみで完全マッチングができない
0を含んでいる成分がなくなるように行・列を削除して行列B生成 (削除する行・列数を最小にする)
for each element in A
if element is not in 削除された行・列
element ← element - min_element_in_B
end if
end for
end while
値が0の成分のみの完全マッチングを出力
9. 解法
9.1 厳密解法
9.1.1 分枝限定法 (Branch and Bound)
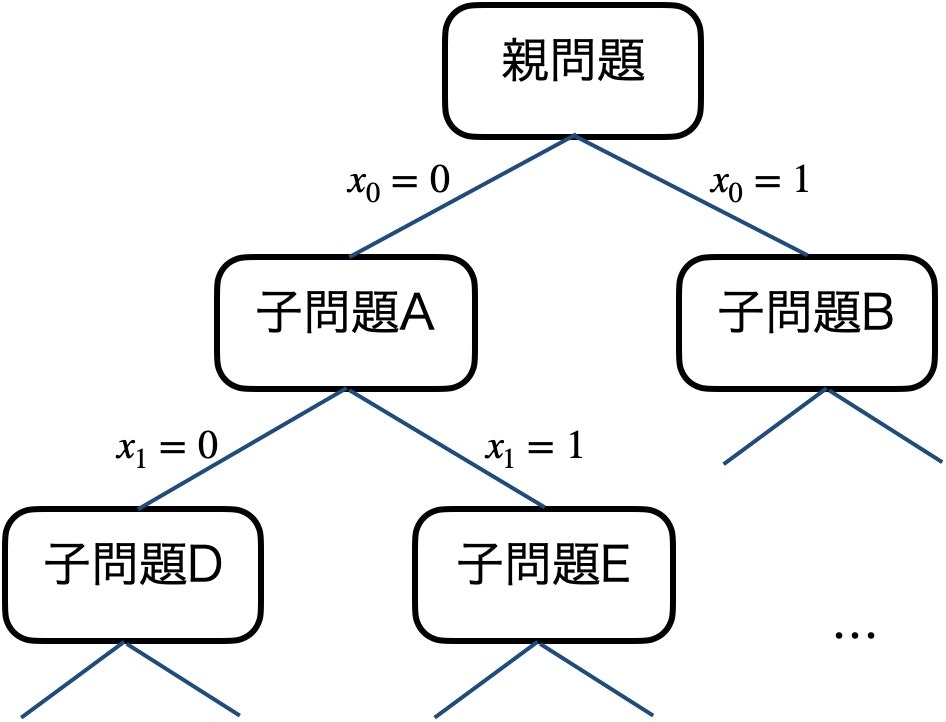
変数の値で場合分けして元の問題を子問題に分割する操作と (分枝操作)、子問題以下に最適解が存在するかを確認する操作 (限定操作) とを繰り返して解を求める手法。
全探索をベースとして厳密解法だが、処理を途中で止めれば暫定解が得られる。
ナップザック問題を例にとると以下のように処理される。
- 貪欲法などで初期解を得る。初期解はこの問題の下界。
- まだ検討していない品物を選んだ場合と選ばなかった場合でそれぞれ子問題を作る (分枝操作)
- 子問題では線形緩和により解を得て、解の値が下界以下ならその子問題は切り捨てる (限定操作)。捨てない場合は子問題を再帰的に解く。いずれかの子問題で解が得られれば、下界を更新する。
- すべての子問題が解き、下界に対応する
9.1.2 切除平面法 (Cutting-Plane Method)
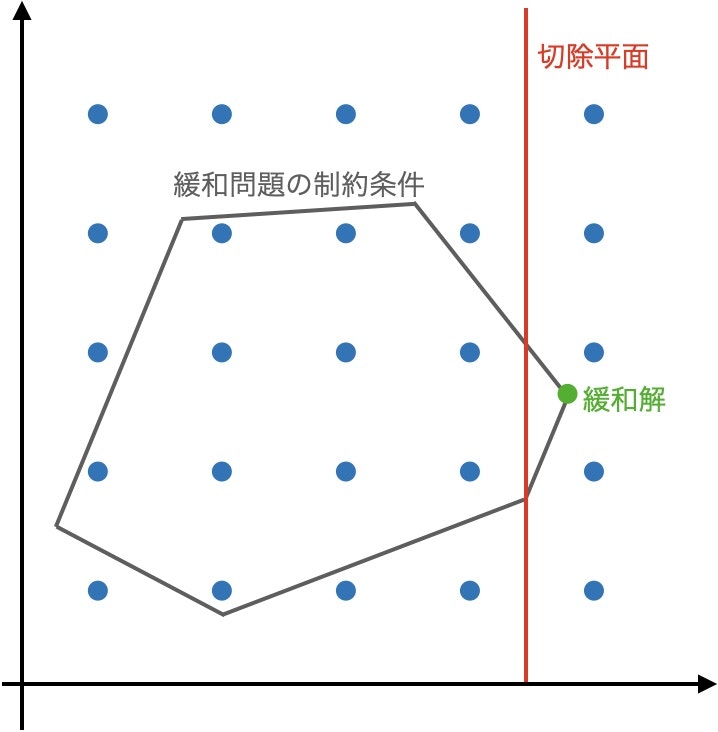
線形緩和問題の最適解から始めて、整数解を残しつつ緩和解を除去する制約を追加する手続きを繰り返し適用する。妥当不等式 (整数解を残す制約) の中で緩和解を除くものを切除平面と言い、切除平面を追加することで解空間を狭めていく。
- 線形緩和問題を解く
- 緩和解が整数解なら終了
- 妥当不等式を追加して1.に戻る
9.2 近似解法
9.2.1 貪欲法
問題の意思決定対象に対し、局所的な情報だけで順に意思決定していく。例えばナップザック問題で、$p_i/w_i$ が大きいものから順に商品を選んでいくなど。
一般には近似解しか得られないが、クラスカル法・プリム法・ジョンソン法などでは厳密解を得られる。
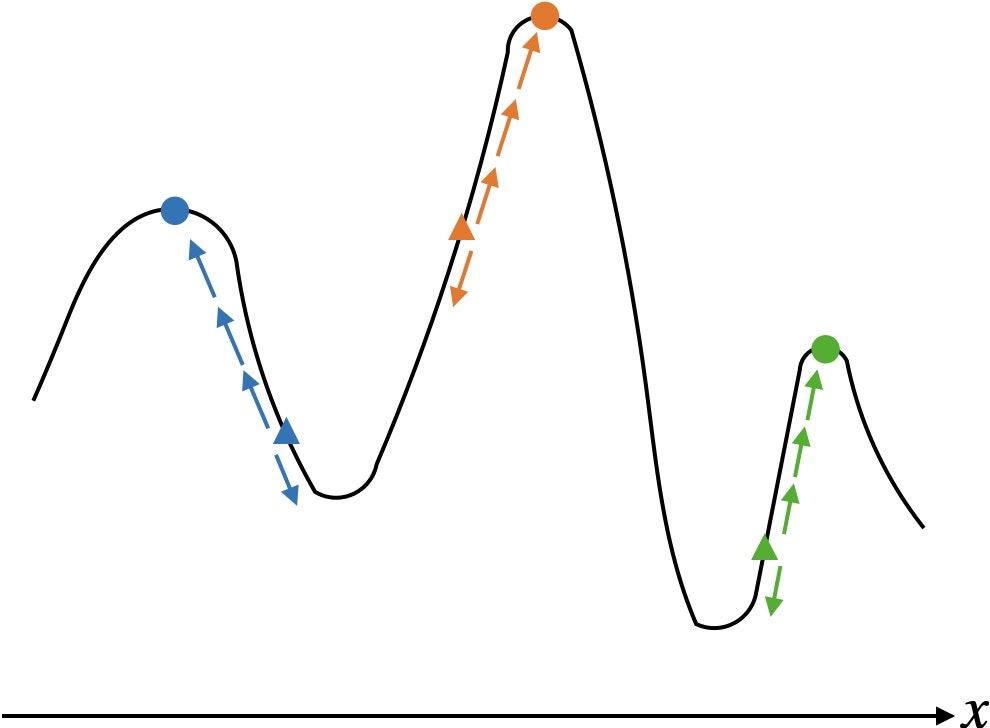
9.2.2 局所探索法
名前の通り今得られている解の近傍を探索していく。
- 初期解 $\boldsymbol{x}$ をいずれかの方法により構築する
- 解 $\boldsymbol{x}$ の近傍内によりよい解があれば解 $\boldsymbol{x}$ を更新し、ステップ2に戻る。よりよい解がなければ終了する。
ナップザック問題を例にとると近傍には以下のようなものがある。
- 挿入近傍:リストに入っていない品物を1つ選び、リストに入れる
- 交換近傍:リストに入っているものから1つ、入っていないものから1つ選び交換する
- $k$-opt近傍:$k$ 個の要素を変化させる。リストに入っているものから $k-l$ 個、入っていないものから $l$ 個選び交換する、など
一般に大域的最適解には到達できないが、局所的最適解は比較的容易に求められる。
9.2.3 メタヒューリスティクス
問題に依存しない形式で近似的に解を探索・改善する手法。以下のような工夫によりよい解を得られる。これらをバランスよく実現することが重要。
- 集中化:よい解周辺を集中的に探索する
- 多様化:局所的最適解に陥らないように、幅広く探索する
9.2.3.1 多スタート局所探索法 (Multi-start Local Search)
初期解を変えて局所探索法を繰り返す方法。初期解の作成には乱数を用いる。
途中までの局所最適解を初期解に反映させる方法もある。適応的多スタート局所探索法という。
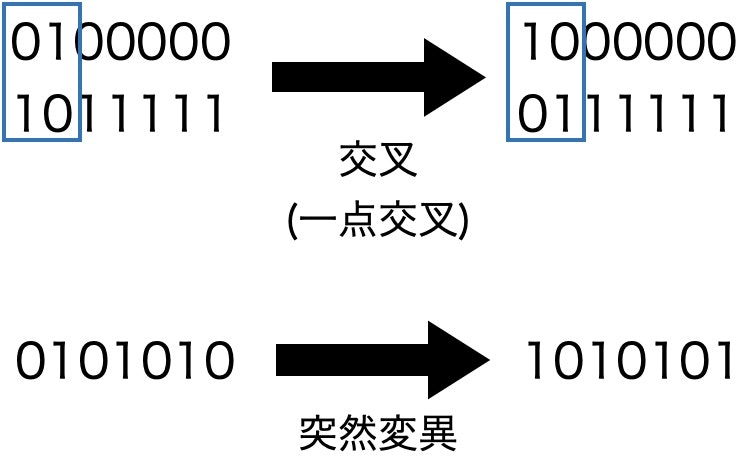
9.2.3.2 遺伝的アルゴリズム (Generic Algorithm)
解を遺伝子として表現し、複数の遺伝子を用いて交叉や突然変異などの操作と淘汰による世代交代によって、解を探索する。
交叉や突然変異は以下のイメージ。
9.2.3.3. 粒子群最適化 (Particle Swarm Optimization)
多数の粒子によって集団を形成し、集団に含まれる粒子同士が情報交換することにより探索を進める。
- 初期化:すべての粒子 $k$ に対して、初期位置 $x_k(0)$ と初期速度 $v_k(0)$ を与える
- 位置更新:速度を用いて粒子の位置を更新する。$x_k(t+1)=x_k(t)+v_k(t)$
- 速度更新:よい解の方向に向かうように速度を更新する。$x_k^p(t)$ は $k$ 番目の粒子の中での過去最良解、$x^g(t)$ はタイムステップ $t$ における最良解、$w, c, r$ は定数。
v_k(t+1)=wv_k(t)+c_1r_1\left(x^{p}_k(t)-x_k(t+1)\right)+c_2r_2\left(x^{g}(t)-x_k(t+1)\right)
9.2.3.4. 焼きなまし法 (Simulated Annealing)
高温状態からはじめ、探索を繰り返す中で低音状態にしていく。高温では改悪を含む探索を許容、低温では通常の局所探索をすることで、局所最適解に陥らないようにする。
- 初期温度 $T$ を設定する
- 初期解を設定する
- 冷却率 $\alpha$ で温度を下げる。$T←\alpha T$。
- 次の解をランダムにサンプリングする。
4-1. サンプリングした解が現在の解よりよい場合、更新する。
4-2. サンプリングした解が現在の解より悪い場合、改悪幅 $\Delta E$ に対して確率 $\displaystyle Prob\left(U(0,1)>\exp\left(-\frac{\Delta E}{T}\right)\right)$ で更新する。 - 閾値を満たす解を得られるまで3.と4.を繰り返す。
9.2.3.5. 人工蜂コロニーアルゴリズム (Artificial Bee Colony Algorithm)
ミツバチの採餌行動を模す。収穫バチ・追従バチ・偵察バチを定義。
- 収穫バチ:1つの食糧源に蜜を取りに行き、その近傍も探索する
- 追従バチ:収穫バチの情報に基づいて目標の食糧源を決め、蜜を取りに行く
- 偵察バチ:食糧源の蜜が尽きたら新しい食糧源を決める。
以下のようなアルゴリズム。
- 初期食糧源を生成する
- 収穫バチフェーズ。自分の食糧源近傍を探索し、よりよい食糧源があれば更新する。また、蜜の取得回数をインクリメントする
- 追従バチフェーズ。評価値の高い食糧源を高確率で選択し、蜜の取得回数をインクリメントする
- 偵察バチフェーズ。指定回数以上蜜を取得した食糧源を、他の食糧源に置き換える。探索の打ち切りを示す
9.2.3.6. タブー探索法 (Tabu Search)
タブーリストと呼ばれる過去の更新履歴を用いて、同じ解への探索をしないようにする。局所解に落ちないための工夫。
- 基準個体を生成する
- 近傍個体を生成する (タブーリストに含まれる個体は生成しない)
- 基準個体から最良個体への遷移をタブーリストに追加 (最良個体そのものをタブーリストに追加する場合もある)
- 最良個体を基準個体にする
- 最良個体が終了条件を満たせば終了、それ以外の場合2.に戻る。
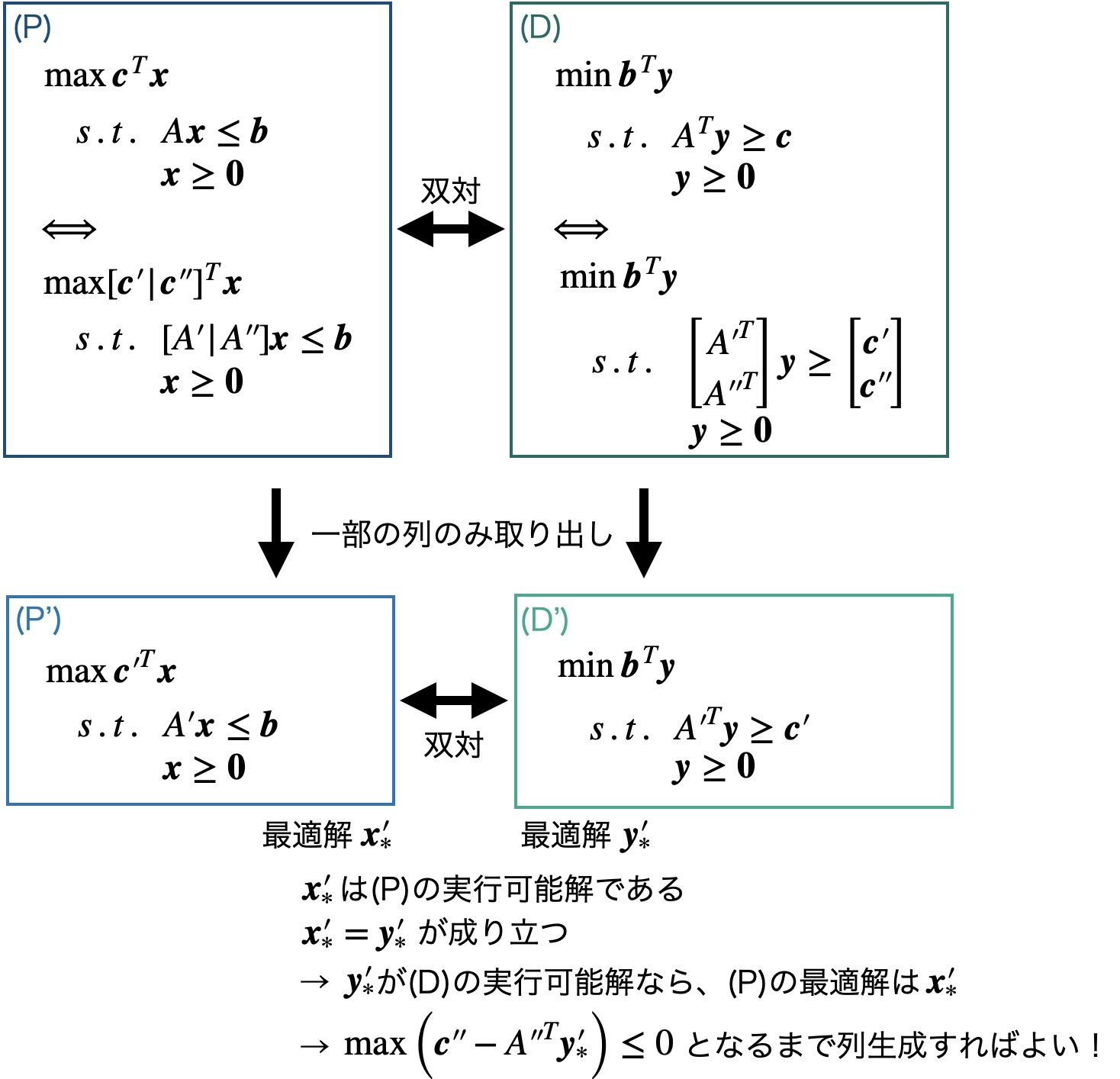
9.2.4. 列生成法 (Column Generation Algorithm)
パターンを全列挙すると膨大になり線形緩和問題を解くのも難しい場合に、パターンを一部だけ列挙して近似解を得る方法。