はじめに
以前の記事で、公式のチュートリアルにそってPyTorchでニューラルネットワークを作成しました。
BERTの実装を最終的な目標としていますが、BERTと同じAttentionベースのモデルであるTransformerのチュートリアルがPyTorchの公式にあったので、今回はこれにそってTransformerを作成してみます。
PyTorchによるTransformerの作成
今回は、Transformerに、途中で切れた文が与えられた時に、次にくる単語が何であるかを推測するタスクでTransformerの学習を行います。
環境作成
ここではMac OSでpipを使った場合の環境作成方法を説明します(使用したOSはMac OS 12.3.1)。
その他の場合は、こちらを参考に環境を構築してください。
(1) Homebrewでpython3をインストール
$ brew install python3
(2) pipを使ってPyTorchと今回利用するデータセットをインストール(チュートリアルではtorchtextのインストールに触れられていませんが、エラーになってしまったので追加でインストールしました)
$ pip3 install torch torchdata torchtext
なお、Google Colaboratoryなどのクラウドサービスを使えば、GPUを簡単に利用することができます。
Transformerモデルの作成
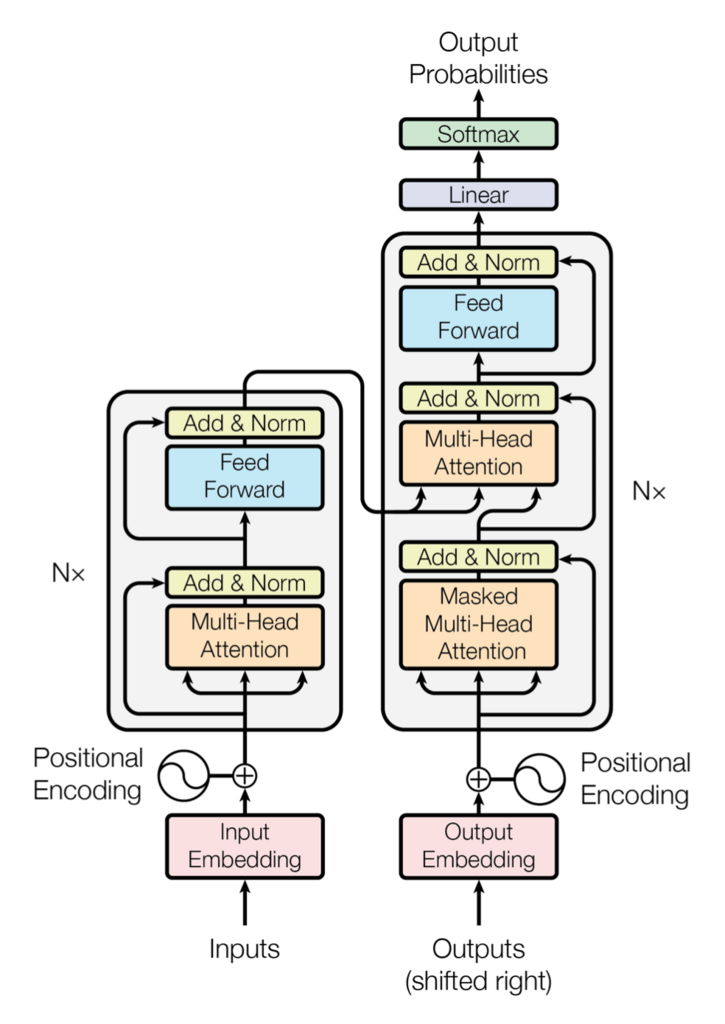
まず、下図に示すTransformerモデルを作成していきます。
Input Embedding
nn.Embeddingモジュールを使って、入力のOne-hotベクトルで表現されている単語を、埋め込みベクトルに変換します。
self.encoder = nn.Embedding(ntoken, d_model)
src = self.encoder(src) * math.sqrt(self.d_model)
Positional Encoding
Transformerでは、単語の位置情報を埋め込みベクトルに付加する必要があります。
そのために、下記のようなモジュールを作成します。
class PositionalEncoding(nn.Module):
def __init__(self, d_model: int, dropout: float = 0.1, max_len: int = 5000):
super().__init__()
self.dropout = nn.Dropout(p=dropout)
position = torch.arange(max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))
pe = torch.zeros(max_len, 1, d_model)
pe[:, 0, 0::2] = torch.sin(position * div_term)
pe[:, 0, 1::2] = torch.cos(position * div_term)
self.register_buffer('pe', pe)
def forward(self, x: Tensor) -> Tensor:
"""
Args:
x: Tensor, shape [seq_len, batch_size, embedding_dim]
"""
x = x + self.pe[:x.size(0)]
return self.dropout(x)
このモジュールを使って、埋め込みベクトルに位置情報を追加します。
self.pos_encoder = PositionalEncoding(d_model, dropout)
src = self.pos_encoder(src)
Multi-Head Attention + Feed Forward
PyTorchでは、図のグレーの部分(Multi-Head Attention + Feed Forward)の層がnn.TransformerEncoderLayerとして提供されています。
また、Transformerではグレー部分の層を複数繰り返してつなげます。この繰り返しのためにnn.TransformerEncoderが用意されています。
encoder_layers = TransformerEncoderLayer(d_model, nhead, d_hid, dropout)
self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)
output = self.transformer_encoder(src, src_mask)
Linear
nn.Linearモジュールで、結果のベクトルを全語彙に該当するベクトルにマッピングします。
この結果のうち最も値の大きい単語が、入力された文(途中で切れている)の次にくる単語となります。
self.decoder = nn.Linear(d_model, ntoken)
output = self.decoder(output)
以下が、作成したTransformerのモデルです。
__init__メソッドでネットワーク構造を定義し、forwardメソッドで入力データに対する処理を実装します。
forwardメソッドの戻り値がネットワークの出力となります。
import math
from typing import Tuple
import torch
from torch import nn, Tensor
import torch.nn.functional as F
from torch.nn import TransformerEncoder, TransformerEncoderLayer
from torch.utils.data import dataset
class TransformerModel(nn.Module):
def __init__(self, ntoken: int, d_model: int, nhead: int, d_hid: int,
nlayers: int, dropout: float = 0.5):
super().__init__()
self.model_type = 'Transformer'
self.pos_encoder = PositionalEncoding(d_model, dropout)
encoder_layers = TransformerEncoderLayer(d_model, nhead, d_hid, dropout)
self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)
self.encoder = nn.Embedding(ntoken, d_model)
self.d_model = d_model
self.decoder = nn.Linear(d_model, ntoken)
self.init_weights()
def init_weights(self) -> None:
initrange = 0.1
self.encoder.weight.data.uniform_(-initrange, initrange)
self.decoder.bias.data.zero_()
self.decoder.weight.data.uniform_(-initrange, initrange)
def forward(self, src: Tensor, src_mask: Tensor) -> Tensor:
"""
Args:
src: Transformerへの入力データ
src_mask: 入力データにかけるマスク
Returns:
Transformerの出力
"""
src = self.encoder(src) * math.sqrt(self.d_model)
src = self.pos_encoder(src)
output = self.transformer_encoder(src, src_mask)
output = self.decoder(output)
return output
データセットの読み込み
今回はデータセットとして、WikiText2を使います。
WikiText2は、環境構築で既にダウンロード済みです。
テキストのOne-hotベクトル化
data_processメソッドで、WikiText2内の各単語を1次元のOne-hotベクトルに変換します。
from torchtext.datasets import WikiText2
from torchtext.data.utils import get_tokenizer
from torchtext.vocab import build_vocab_from_iterator
train_iter = WikiText2(split='train')
tokenizer = get_tokenizer('basic_english')
vocab = build_vocab_from_iterator(map(tokenizer, train_iter), specials=['<unk>'])
vocab.set_default_index(vocab['<unk>'])
def data_process(raw_text_iter: dataset.IterableDataset) -> Tensor:
data = [torch.tensor(vocab(tokenizer(item)), dtype=torch.long) for item in raw_text_iter]
return torch.cat(tuple(filter(lambda t: t.numel() > 0, data)))
# train_iterはvocabの構築で消費されるため、ここでもう一度作成する
train_iter, val_iter, test_iter = WikiText2()
train_data = data_process(train_iter)
val_data = data_process(val_iter)
test_data = data_process(test_iter)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
ミニバッチ作成
並列処理を可能にするために、batchifyメソッドを使って、入力データをいくつかのグループ(ミニバッチ)に分割します。グループの数は引数のbszで指定します。
例えば、dataとして下記のような26文字のアルファベットからなるベクトル、
\left[
\begin{array}{ccccccc}
A & B & C & \ldots & X & Y & Z
\end{array}
\right]
bsz(バッチサイズ)を4とした場合、出力は下記のようになります。
\begin{eqnarray}
\left[
\begin{array}{cccc}
\left[
\begin{array}{c}
A\\B\\C\\D\\E\\F
\end{array}
\right]&
\left[
\begin{array}{c}
G\\H\\I\\J\\K\\L
\end{array}
\right]&
\left[
\begin{array}{c}
M\\N\\O\\P\\Q\\R
\end{array}
\right]&
\left[
\begin{array}{c}
S\\T\\U\\V\\W\\X
\end{array}
\right]
\end{array}
\right]
\end{eqnarray}
def batchify(data: Tensor, bsz: int) -> Tensor:
"""
Args:
data: 入力データ
bsz: バッチサイズ
Returns:
ミニバッチ
"""
seq_len = data.size(0) // bsz
data = data[:seq_len * bsz]
data = data.view(bsz, seq_len).t().contiguous()
return data.to(device)
batch_size = 20
eval_batch_size = 10
train_data = batchify(train_data, batch_size) # shape [seq_len, batch_size]
val_data = batchify(val_data, eval_batch_size)
test_data = batchify(test_data, eval_batch_size)
学習用データ、正解データの作成
get_batchメソッドを使って、学習用データ(または検証用データ)と正解データを作成します。
正解データは、学習用データの単語列を、1単語前にずらした単語列となります。
先程のアルファベットのミニバッチを入力とし、iを0、bpttを2とした場合、get_batchの出力は以下のようになります(左が学習用データ、右が訓練用データ)。
\begin{eqnarray}
\left(
\begin{array}{ccc}
\left[
\begin{array}{c}
\left[
\begin{array}{cccc}
A & G & M & S
\end{array}
\right]\\
\left[
\begin{array}{cccc}
B & H & N & T
\end{array}
\right]
\end{array}
\right]
& , &
\left[
\begin{array}{c}
\left[
\begin{array}{cccc}
B & H & N & T
\end{array}
\right]\\
\left[
\begin{array}{cccc}
C & I & O & U
\end{array}
\right]
\end{array}
\right]
\end{array}
\right)
\end{eqnarray}
bptt = 35
def get_batch(source: Tensor, i: int) -> Tuple[Tensor, Tensor]:
"""
Args:
source: ミニバッチ
i: int
Returns:
学習用データ、正解データのtuple (data, target)
"""
seq_len = min(bptt, len(source) - 1 - i)
data = source[i:i+seq_len]
target = source[i+1:i+1+seq_len].reshape(-1)
return data, target
マスキング
generate_square_subsequent_maskを使って、Transformerが学習を行う際に、現在注目している単語に後続する単語を参照できなくします。
def generate_square_subsequent_mask(sz: int) -> Tensor:
return torch.triu(torch.ones(sz, sz) * float('-inf'), diagonal=1)
学習と検証
ここから、Transformerを使った学習と検証を説明します。大まかな流れは、以前作成したニューラルネットワークの時と同じです。
損失関数
Transformerの学習では、出力と正解との誤差(損失関数)を計算し、損失関数の値が小さくなるようにしていきます。
今回は、多クラス分類の学習であるため交差エントロピー誤差(cross entropy error)を損失関数として使います。PyTorchではnn.CrossEntropyLossとして提供されています。
criterion = nn.CrossEntropyLoss()
最適化
最適化とは、先ほど説明した損失関数の値が小さくなるように、Transformerのパラメーター(重み、バイアス)を調整することです。パラメーターの調整量のことを勾配(gradient)と呼びます。
今回は最適化アルゴリズムの1つである確率的勾配降下法(stochastic gradient descent, SDG)を使用します。PyTorchではtorch.optim.SGDとして提供されています。
torch.optim.SGDには、モデルのパラメーターと学習係数を指定します。学習係数によりパラメーターの更新量を調整することができます。
lr = 5.0 # 学習係数
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
学習
ミニバッチ単位で以下の手順を実行し、学習を行います。
(1) Transformerに学習用データを入力し、出力を得る。
# data: Transformerへの入力、src_mask: dataにかけるマスク、model: Transformerモデル、output: Transformerからの出力
output = model(data, src_mask)
(2) 出力と正解から損失関数を計算する。
# output: Transformerからの出力、targets: 正解、criterion: 損失関数
loss = criterion(output.view(-1, ntokens), targets)
(3) 勾配の値をリセットする(0にする)。
optimizer.zero_grad()
(4) 損失関数から誤差逆伝播法(back propagation)により、Transformerの全パラメーターの勾配を計算する。勾配計算はPyTorch組み込みの微分エンジンtorch.autogradにより行われています。詳細を知りたい方はこちらをご覧ください。
loss.backward()
(5) 計算した勾配を用いて、全パラメーターの値を更新する
optimizer.step()
以下は、上記の手順をまとめたメソッドです。
import copy
import time
ntokens = len(vocab) # 語彙数
emsize = 200 # 埋め込みベクトルの次元
d_hid = 200 # nn.TransformerEncoderのフィードフォワードネットワークの次元
nlayers = 2 # nn.TransformerEncoder内のnn.TransformerEncoderLayerの数
nhead = 2 # nn.MultiheadAttention内のヘッドの数
dropout = 0.2 # dropoutの割合
model = TransformerModel(ntokens, emsize, nhead, d_hid, nlayers, dropout).to(device)
criterion = nn.CrossEntropyLoss()
lr = 5.0 # learning rate
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 1.0, gamma=0.95)
def train(model: nn.Module) -> None:
model.train() # 学習モードに切り替え
total_loss = 0.
log_interval = 200
start_time = time.time()
src_mask = generate_square_subsequent_mask(bptt).to(device)
num_batches = len(train_data) // bptt
for batch, i in enumerate(range(0, train_data.size(0) - 1, bptt)):
data, targets = get_batch(train_data, i)
batch_size = data.size(0)
if batch_size != bptt: # 最後のバッチの時のみ
src_mask = src_mask[:batch_size, :batch_size]
output = model(data, src_mask)
loss = criterion(output.view(-1, ntokens), targets)
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 0.5)
optimizer.step()
total_loss += loss.item()
if batch % log_interval == 0 and batch > 0:
lr = scheduler.get_last_lr()[0]
ms_per_batch = (time.time() - start_time) * 1000 / log_interval
cur_loss = total_loss / log_interval
ppl = math.exp(cur_loss)
print(f'| epoch {epoch:3d} | {batch:5d}/{num_batches:5d} batches | '
f'lr {lr:02.2f} | ms/batch {ms_per_batch:5.2f} | '
f'loss {cur_loss:5.2f} | ppl {ppl:8.2f}')
total_loss = 0
start_time = time.time()
検証
検証では、検証データをTransformerに入力し、得られた出力と正解との誤差を計算します。
検証では学習が不要なため、torch.no_grad()によって勾配計算に必要な処理を無効にします(処理性能向上のため)。
def evaluate(model: nn.Module, eval_data: Tensor) -> float:
model.eval() # 検証モードに切り替え
total_loss = 0.
src_mask = generate_square_subsequent_mask(bptt).to(device)
with torch.no_grad():
for i in range(0, eval_data.size(0) - 1, bptt):
data, targets = get_batch(eval_data, i)
batch_size = data.size(0)
if batch_size != bptt:
src_mask = src_mask[:batch_size, :batch_size]
output = model(data, src_mask)
output_flat = output.view(-1, ntokens)
total_loss += batch_size * criterion(output_flat, targets).item()
return total_loss / (len(eval_data) - 1)
プログラムの実行
最後に、下記のプログラムで3エポックの学習(train)+検証(evaluate)を繰り返します。
best_val_loss = float('inf')
#エポック数
epochs = 3
best_model = None
for epoch in range(1, epochs + 1):
epoch_start_time = time.time()
train(model)
val_loss = evaluate(model, val_data)
val_ppl = math.exp(val_loss)
elapsed = time.time() - epoch_start_time
print('-' * 89)
print(f'| end of epoch {epoch:3d} | time: {elapsed:5.2f}s | '
f'valid loss {val_loss:5.2f} | valid ppl {val_ppl:8.2f}')
print('-' * 89)
if val_loss < best_val_loss:
best_val_loss = val_loss
best_model = copy.deepcopy(model)
scheduler.step()
その際の出力結果がこちらです。学習が進むにつれ正解率(Accuracy)が上昇し、誤差(loss)が小さくなっていることが確認できます。
ちなみに、GPUは使っていないため、3エポックでもかなりの時間がかかりました。実際に試してみる方は、Google Colaboratoryでの実行をおすすめします。
| epoch 1 | 200/ 2928 batches | lr 5.00 | ms/batch 420.44 | loss 8.01 | ppl 3018.63
| epoch 1 | 400/ 2928 batches | lr 5.00 | ms/batch 434.12 | loss 6.86 | ppl 950.57
| epoch 1 | 600/ 2928 batches | lr 5.00 | ms/batch 440.21 | loss 6.42 | ppl 615.38
| epoch 1 | 800/ 2928 batches | lr 5.00 | ms/batch 436.10 | loss 6.29 | ppl 540.35
| epoch 1 | 1000/ 2928 batches | lr 5.00 | ms/batch 440.15 | loss 6.18 | ppl 480.69
| epoch 1 | 1200/ 2928 batches | lr 5.00 | ms/batch 430.71 | loss 6.15 | ppl 468.42
| epoch 1 | 1400/ 2928 batches | lr 5.00 | ms/batch 424.53 | loss 6.11 | ppl 449.43
| epoch 1 | 1600/ 2928 batches | lr 5.00 | ms/batch 426.39 | loss 6.10 | ppl 445.31
| epoch 1 | 1800/ 2928 batches | lr 5.00 | ms/batch 422.44 | loss 6.02 | ppl 411.21
| epoch 1 | 2000/ 2928 batches | lr 5.00 | ms/batch 412.33 | loss 6.01 | ppl 407.06
| epoch 1 | 2200/ 2928 batches | lr 5.00 | ms/batch 417.48 | loss 5.89 | ppl 359.91
| epoch 1 | 2400/ 2928 batches | lr 5.00 | ms/batch 430.99 | loss 5.96 | ppl 389.16
| epoch 1 | 2600/ 2928 batches | lr 5.00 | ms/batch 440.37 | loss 5.95 | ppl 383.34
| epoch 1 | 2800/ 2928 batches | lr 5.00 | ms/batch 433.94 | loss 5.88 | ppl 357.36
-----------------------------------------------------------------------------------------
| end of epoch 1 | time: 1303.18s | valid loss 5.81 | valid ppl 334.50
-----------------------------------------------------------------------------------------
| epoch 2 | 200/ 2928 batches | lr 4.75 | ms/batch 448.69 | loss 5.85 | ppl 347.13
| epoch 2 | 400/ 2928 batches | lr 4.75 | ms/batch 451.74 | loss 5.84 | ppl 344.30
| epoch 2 | 600/ 2928 batches | lr 4.75 | ms/batch 442.30 | loss 5.65 | ppl 285.24
| epoch 2 | 800/ 2928 batches | lr 4.75 | ms/batch 450.91 | loss 5.69 | ppl 296.31
| epoch 2 | 1000/ 2928 batches | lr 4.75 | ms/batch 461.74 | loss 5.64 | ppl 282.26
| epoch 2 | 1200/ 2928 batches | lr 4.75 | ms/batch 464.20 | loss 5.67 | ppl 290.53
| epoch 2 | 1400/ 2928 batches | lr 4.75 | ms/batch 433.12 | loss 5.68 | ppl 293.03
| epoch 2 | 1600/ 2928 batches | lr 4.75 | ms/batch 433.08 | loss 5.70 | ppl 299.90
| epoch 2 | 1800/ 2928 batches | lr 4.75 | ms/batch 446.36 | loss 5.64 | ppl 281.13
| epoch 2 | 2000/ 2928 batches | lr 4.75 | ms/batch 443.56 | loss 5.66 | ppl 286.80
| epoch 2 | 2200/ 2928 batches | lr 4.75 | ms/batch 445.23 | loss 5.54 | ppl 255.44
| epoch 2 | 2400/ 2928 batches | lr 4.75 | ms/batch 454.44 | loss 5.63 | ppl 279.42
| epoch 2 | 2600/ 2928 batches | lr 4.75 | ms/batch 451.50 | loss 5.63 | ppl 279.43
| epoch 2 | 2800/ 2928 batches | lr 4.75 | ms/batch 456.88 | loss 5.57 | ppl 262.01
-----------------------------------------------------------------------------------------
| end of epoch 2 | time: 1361.26s | valid loss 5.65 | valid ppl 284.21
-----------------------------------------------------------------------------------------
| epoch 3 | 200/ 2928 batches | lr 4.51 | ms/batch 443.37 | loss 5.59 | ppl 268.65
| epoch 3 | 400/ 2928 batches | lr 4.51 | ms/batch 476.49 | loss 5.61 | ppl 272.55
| epoch 3 | 600/ 2928 batches | lr 4.51 | ms/batch 466.81 | loss 5.41 | ppl 222.53
| epoch 3 | 800/ 2928 batches | lr 4.51 | ms/batch 447.77 | loss 5.47 | ppl 236.85
| epoch 3 | 1000/ 2928 batches | lr 4.51 | ms/batch 447.26 | loss 5.42 | ppl 225.61
| epoch 3 | 1200/ 2928 batches | lr 4.51 | ms/batch 444.40 | loss 5.46 | ppl 235.93
| epoch 3 | 1400/ 2928 batches | lr 4.51 | ms/batch 461.98 | loss 5.49 | ppl 241.44
| epoch 3 | 1600/ 2928 batches | lr 4.51 | ms/batch 433.08 | loss 5.52 | ppl 249.04
| epoch 3 | 1800/ 2928 batches | lr 4.51 | ms/batch 426.84 | loss 5.46 | ppl 234.91
| epoch 3 | 2000/ 2928 batches | lr 4.51 | ms/batch 426.60 | loss 5.48 | ppl 238.70
| epoch 3 | 2200/ 2928 batches | lr 4.51 | ms/batch 5334.73 | loss 5.35 | ppl 210.36
| epoch 3 | 2400/ 2928 batches | lr 4.51 | ms/batch 450.23 | loss 5.46 | ppl 234.02
| epoch 3 | 2600/ 2928 batches | lr 4.51 | ms/batch 453.25 | loss 5.47 | ppl 238.04
| epoch 3 | 2800/ 2928 batches | lr 4.51 | ms/batch 468.60 | loss 5.39 | ppl 219.83
-----------------------------------------------------------------------------------------
| end of epoch 3 | time: 2341.51s | valid loss 5.60 | valid ppl 269.74
-----------------------------------------------------------------------------------------
まとめ
前回のPyTorchを使ったニューラルネットワークの作成に続き、今回はTransformerモデルの作成をしましたが、入力データ、モデルの作成以外は、ほぼ同じ実装なことに気づきました。
PyTorchでのCNNやRNNは未経験なので同じパターンかどうかわかりませんが、このパターンは覚えておいて損はなさそうです。
次回からは、これまで学習してきた内容をもとに、PyTorchを使ってBERTの実装をしてみようと思います。
今回作成したプログラムはGitHubで公開しています。
https://github.com/age884/qiita_transformer/blob/main/transformer.py