はじめに
PyTorchはTensorFlowと並び称される機械学習フレームワークです。
以前、TensorFlowを使ってBERTの実装をしたことがありますが、カスタマイズに苦労しました。
PyTorchの特徴として、カスタマイズのしやすさがあるということなので、今度はPyTorchを使ってBERTの実装に挑戦しようと思います。
今回は、PyTorchに親しむために公式のチュートリアルにそってニューラルネットワークを作成し、PyTorchの基礎についてまとめます。
PyTorchによるニューラルネットワークの作成
環境作成
ここではMac OSでpipを使った場合の環境作成方法を説明します(使用したOSはMac OS 12.2.1)。
その他の場合は、こちらを参考に環境を構築してください。
(1) Homebrewでpython3をインストール
$ brew install python3
(2) pipを使ってPyTorchをインストール
$ pip3 install torch torchvision
なお、Google Colaboratoryなどのクラウドサービスを使えば、GPUを簡単に利用することができます。
Tensor
PyTorchではTensorというデータ構造で、モデルの入力、出力、そしてパラメーターを表現します。
TensorはNumPyの多次元配列データ構造ndarrayに似ています。しかしndarrayとは異なり、GPU上で実行が可能です。
データセットの準備
PyTorchでは、torch.utils.data.Datasetのサブクラスとして多くのデータセットが提供されています。
今回は、そのうちの一つであるFashion-MNISTデータセットを使用します。このデータセットには6万の学習用データと1万の検証用データが含まれています。
各データは、28×28ピクセルのグレースケール画像と、その画像が何であるかを示すラベル(0: T-Shirt, 1: Trouser, 2: Pullover, 3: Dress, 4: Coat, 5: Sandal, 6: Shirt, 7: Sneaker, 8: Bag, 9: Ankle Boot)で構成されています。
今回扱うFashion-MNISTデータセットに対しては、FashionMNISTクラスを使います。
FashionMNISTのパラーメーターには、以下のものを指定します。
- root: データが格納されているディレクトリ
- train: 学習用データの場合はTrue、検証用データの場合はFalseを指定します
- download: Trueの場合は、rootで指定したディレクトリにデータがない場合に、インターネットからダウンロードします
- transform: 画像の変換方法
ToTensor()は画像をFloatTensor型に変換します。
from torchvision import datasets
#訓練用データ
training_data = datasets.FashionMNIST(
root="data",
train=True,
download=True,
transform=ToTensor()
)
#検証用データ
test_data = datasets.FashionMNIST(
root="data",
train=False,
download=True,
transform=ToTensor()
)
独自のデータをデータセットとして使いたい場合は、torch.utils.data.Datasetを継承して独自のDatasetクラスを作成します。
詳細はこちらをご覧ください。
データセットの読み込み
データセットの読み込みには、PyTorchで提供されているtorch.utils.data.DataLoaderを使います。
DataLoaderはDatasetをIterableとしてラップしたものです。
学習、検証の際には、何枚かの画像を1セット(ミニバッチ)として処理をしますが、このミニバッチのサイズをDataLoaderの引数として渡します。
また、入力画像がランダムな順に読み込まれるように、shuffle=Trueを指定します。
from torch.utils.data import DataLoader
#ミニバッチのサイズ
batch_size = 64
#訓練用データの読み込み
train_dataloader = DataLoader(training_data, batch_size=batch_size, shuffle=True)
#検証用データの読み込み
test_dataloader = DataLoader(test_data, batch_size=batch_size, shuffle=True)
ニューラルネットワークの作成
PyTorchでは、nn.Moduleのサブクラスとしてニューラルネットワークを定義します。
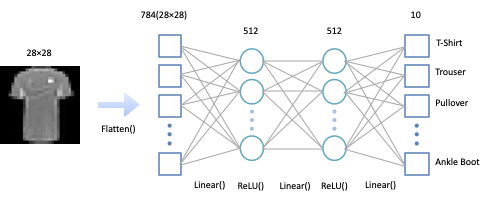
ここでは、PyTorchで提供されているnn.Modleのサブクラスであるnn.Flatten、nn.Linear、nn.ReLU、nn.Sequentialを組み合わせて、下図のようなニューラルネットワークを構築します。
nn.Flatten
画像に対応するの2次元Tensor(size=28×28)を1次元のTensor(size=784)に変換します。
nn.Linear
入力の重み付き総和とバイアスとの和を計算します。
nn.ReLU
活性化関数の1つ。負の値を0に変換します。
[2.8, -1.2, 0.3] → [2.8, 0, 0.3]
nn.Sequential
モジュールをつなげて、入力に対して連続的に処理を行なっていきます。
以下が、作成したニューラルネットワークです。
__init__メソッドでネットワーク構造を定義し、forwardメソッドで入力データに対する処理を実装します。
forwardメソッドの戻り値がネットワークの出力となります。
from torch import nn
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(28*28, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 10),
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
作成したニューラルネットワークを、以下のようにしてデバイス上に配置します。
import torch
device = "cuda" if torch.cuda.is_available() else "cpu"
model = NeuralNetwork().to(device)
学習と検証
損失関数
ニューラルネットワークの学習では、出力と正解との誤差(損失関数)を計算し、損失関数の値が小さくなるように学習をします。
今回は、多クラス分類の学習であるため交差エントロピー誤差(cross entropy error)を損失関数として使います。PyTorchではnn.CrossEntropyLossとして提供されています。
loss_fn = nn.CrossEntropyLoss()
最適化
最適化とは、先ほど説明した損失関数の値が小さくなるように、ニューラルネットワークのパラメーター(重み、バイアス)を調整することです。パラメーターの調整量のことを勾配(gradient)と呼びます。
今回は最適化アルゴリズムの1つである確率的勾配降下法(stochastic gradient descent, SDG)を使用します。PyTorchではtorch.optim.SGDとして提供されています。
torch.optim.SGDには、モデルのパラメーターと学習係数を指定します。学習係数によりパラメーターの更新量を調整することができます。
#学習係数
learning_rate = 1e-3
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
学習
ミニバッチ単位で以下の手順を実行し、学習を行います。
(1) ニューラルネットワークに学習用データを入力し、出力を得る。
#X: 学習用データ、model: ニューラルネットワーク、pred: 出力
pred = model(X)
(2) 出力と正解から損失関数を計算する。
#pred: 出力、y: 正解、loss_fn: 損失関数
loss = loss_fn(pred, y)
(3) 勾配の値をリセットする(0にする)。
optimizer.zero_grad()
(4) 損失関数から誤差逆伝播法(back propagation)により、ニューラルネットワーク内の全パラメーターの勾配を計算する。勾配計算はPyTorch組み込みの微分エンジンtorch.autogradにより行われています。詳細を知りたい方はこちらをご覧ください。
loss.backward()
(5) 計算した勾配を用いて、全パラメーターの値を更新する
optimizer.step()
以下は、上記の手順をまとめたメソッドです。
def train_loop(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
for batch, (X, y) in enumerate(dataloader):
#ニューラルネットワークの出力
pred = model(X)
#損失関数
loss = loss_fn(pred, y)
#誤差逆伝播
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch % 100 == 0:
loss, current = loss.item(), batch * len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
検証
検証では、検証データをニューラルネットワークに入力し、得られた出力と正解との誤差を計算します。
検証では学習が不要なため、torch.no_grad()によって勾配計算に必要な処理を無効にします(処理性能向上のため)。
def test_loop(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
pred = model(X)
test_loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
プログラムの実行
最後に、下記のプログラムで10エポックの学習+検証を繰り返します。
#エポック数
epochs = 10
for t in range(epochs):
print(f"Epoch {t+1}\n-------------------------------")
train_loop(train_dataloader, model, loss_fn, optimizer)
test_loop(test_dataloader, model, loss_fn)
print("Done!")
その際の出力結果がこちらです。学習が進むにつれ正解率(Accuracy)が上昇し、誤差(loss)が小さくなっていることが確認できます。
Epoch 1
-------------------------------
loss: 2.308301 [ 0/60000]
loss: 2.282357 [ 6400/60000]
loss: 2.281907 [12800/60000]
loss: 2.266773 [19200/60000]
loss: 2.249853 [25600/60000]
loss: 2.241469 [32000/60000]
loss: 2.219312 [38400/60000]
loss: 2.196299 [44800/60000]
loss: 2.181462 [51200/60000]
loss: 2.192415 [57600/60000]
Test Error:
Accuracy: 47.9%, Avg loss: 2.150180
Epoch 2
-------------------------------
loss: 2.124759 [ 0/60000]
loss: 2.131443 [ 6400/60000]
loss: 2.104781 [12800/60000]
loss: 2.071867 [19200/60000]
loss: 2.038198 [25600/60000]
loss: 2.003879 [32000/60000]
loss: 1.980923 [38400/60000]
loss: 1.987780 [44800/60000]
loss: 1.875359 [51200/60000]
loss: 1.905337 [57600/60000]
Test Error:
Accuracy: 55.8%, Avg loss: 1.872483
Epoch 3
-------------------------------
loss: 1.921341 [ 0/60000]
loss: 1.855085 [ 6400/60000]
loss: 1.831424 [12800/60000]
loss: 1.744574 [19200/60000]
loss: 1.704655 [25600/60000]
loss: 1.708343 [32000/60000]
loss: 1.642833 [38400/60000]
loss: 1.588720 [44800/60000]
loss: 1.547683 [51200/60000]
loss: 1.498120 [57600/60000]
Test Error:
Accuracy: 60.9%, Avg loss: 1.512527
Epoch 4
-------------------------------
loss: 1.448732 [ 0/60000]
loss: 1.442486 [ 6400/60000]
loss: 1.488690 [12800/60000]
loss: 1.276109 [19200/60000]
loss: 1.383281 [25600/60000]
loss: 1.397246 [32000/60000]
loss: 1.326674 [38400/60000]
loss: 1.395975 [44800/60000]
loss: 1.274610 [51200/60000]
loss: 1.193545 [57600/60000]
Test Error:
Accuracy: 61.5%, Avg loss: 1.256534
Epoch 5
-------------------------------
loss: 1.235790 [ 0/60000]
loss: 1.250143 [ 6400/60000]
loss: 1.187406 [12800/60000]
loss: 1.277617 [19200/60000]
loss: 1.204994 [25600/60000]
loss: 1.118148 [32000/60000]
loss: 1.168185 [38400/60000]
loss: 1.148146 [44800/60000]
loss: 1.017568 [51200/60000]
loss: 1.056769 [57600/60000]
Test Error:
Accuracy: 63.2%, Avg loss: 1.097873
Epoch 6
-------------------------------
loss: 0.963901 [ 0/60000]
loss: 1.041870 [ 6400/60000]
loss: 1.224379 [12800/60000]
loss: 1.055848 [19200/60000]
loss: 1.106856 [25600/60000]
loss: 1.003040 [32000/60000]
loss: 0.870065 [38400/60000]
loss: 0.893893 [44800/60000]
loss: 1.080920 [51200/60000]
loss: 1.000239 [57600/60000]
Test Error:
Accuracy: 65.3%, Avg loss: 0.995736
Epoch 7
-------------------------------
loss: 0.905157 [ 0/60000]
loss: 1.014492 [ 6400/60000]
loss: 0.934206 [12800/60000]
loss: 0.886744 [19200/60000]
loss: 0.868839 [25600/60000]
loss: 0.939224 [32000/60000]
loss: 0.985162 [38400/60000]
loss: 0.897734 [44800/60000]
loss: 1.097796 [51200/60000]
loss: 0.958092 [57600/60000]
Test Error:
Accuracy: 66.3%, Avg loss: 0.924568
Epoch 8
-------------------------------
loss: 0.833020 [ 0/60000]
loss: 1.027762 [ 6400/60000]
loss: 0.796101 [12800/60000]
loss: 0.934080 [19200/60000]
loss: 0.815363 [25600/60000]
loss: 0.921190 [32000/60000]
loss: 1.076561 [38400/60000]
loss: 0.729981 [44800/60000]
loss: 0.787333 [51200/60000]
loss: 0.905401 [57600/60000]
Test Error:
Accuracy: 67.7%, Avg loss: 0.871649
Epoch 9
-------------------------------
loss: 0.918844 [ 0/60000]
loss: 0.978086 [ 6400/60000]
loss: 0.821040 [12800/60000]
loss: 0.663510 [19200/60000]
loss: 0.760209 [25600/60000]
loss: 0.905184 [32000/60000]
loss: 0.881537 [38400/60000]
loss: 0.776515 [44800/60000]
loss: 0.945093 [51200/60000]
loss: 0.792388 [57600/60000]
Test Error:
Accuracy: 68.4%, Avg loss: 0.832155
Epoch 10
-------------------------------
loss: 0.783152 [ 0/60000]
loss: 0.680521 [ 6400/60000]
loss: 0.683104 [12800/60000]
loss: 0.824782 [19200/60000]
loss: 0.773960 [25600/60000]
loss: 0.897314 [32000/60000]
loss: 0.935476 [38400/60000]
loss: 0.674080 [44800/60000]
loss: 0.671864 [51200/60000]
loss: 0.707593 [57600/60000]
Test Error:
Accuracy: 70.4%, Avg loss: 0.798783
Done!
まとめ
PyTorchで提供されているモジュールを使って、簡単なニューラルネットワークの作成と、その学習を実装しました。ニューラルネットワークの実装は非常に簡単で直感的でしたが、学習部分はややわかりにくいという印象でした。
次回からは、今回学習した基礎をもとに、PyTorchを使ってTransformerの実装をしてみようと思います。