序論
ポケモン世界の「10万ボルト」は、電気袋へのエネルギー蓄積と、そこからの負荷への放電という動的プロセスで理解できます。この放電現象は、時定数 $T$ に支配される一次遅れ系(First-Order Lag System)の典型であり、電気回路のRC自由減衰モデルとして厳密に解析されます。本稿では、このモデルに基づき、ピカチュウの放電特性を時間応答と周波数特性の両面から深掘りします。
1. 厳密なシステム定義と伝達関数
ピカチュウの電気袋をコンデンサ $C$、体内の抵抗と外部負荷抵抗をまとめたものを合成抵抗 $R$ と見なします。
伝達関数 $G(s)$ は、入力 $V_{in}(s)$(充電電源)に対する出力 $V_{out}(s)$(コンデンサ電圧)の比で表されます。
$$
G(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{1}{R C s + 1} = \frac{1}{Ts + 1}
$$
ここで、$T = RC$ は時定数 [s] であり、ピカチュウが電気を蓄え、または放電する速度を決定します。
2. 応答解析の厳密化:蓄積(充電)と放電(減衰)
ピカチュウが技を出すプロセスは、「充電フェーズ」と「放電フェーズ」に分かれます。
(1) エネルギー蓄積フェーズ(充電)
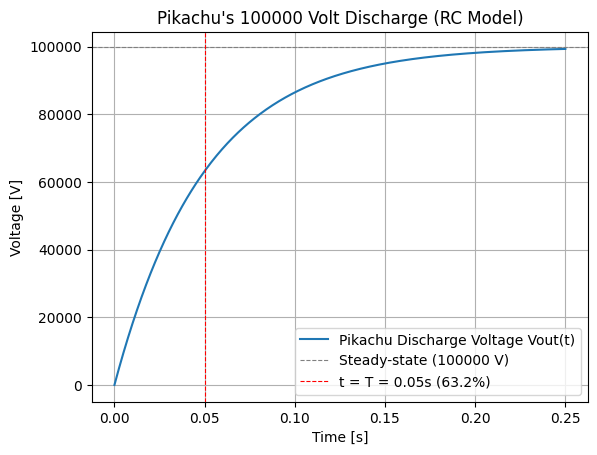
放電命令 $V_{in}$ が $V_0$ のステップ入力として与えられた際の電圧の立ち上がりです。
$$
V_{out, \text{charge}}(t) = V_0(1 - e^{-t/T})
$$
- 物理的意味: $t=T$ で最大電圧 $V_0$ の約 63.2% まで急速に充電されます。この期間は、ピカチュウが電気エネルギーを溜め込んでいる時間に対応します。
(2) 放電フェーズ(自由減衰) - より厳密な「10万ボルト」の持続
蓄積が完了した状態($V_{out}(0)=V_0$)から、負荷抵抗 $R$ を通してエネルギーを消費(放電)する過程です。これが「10万ボルト」の持続時間を厳密にモデル化します。
$$
V_{out, \text{discharge}}(t) = V_0 e^{-t/T}
$$
- 物理的意味: $t=T$ で電圧は初期値 $V_0$ の約 36.8% まで減衰します。これは、放電エネルギーが半減する目安となり、技の持続的な威力が時間と共に減衰する様子を正確に表します。
3. 周波数応答と制御の限界
RC回路の伝達関数 $G(s)$ に $s=j\omega$ を代入して得られる周波数応答 $G(j\omega)$ は、ピカチュウが電気袋の電圧をどれだけ速く制御できるかの限界を示します。
$$
G(j\omega) = \frac{1}{1 + j\omega T}
$$
⚡ ボード線図の制御工学的解釈
一次遅れ系のボード線図は、本質的に**ローパスフィルター(低域通過フィルタ)**として動作します。
つまり、低い周波数の信号(ゆっくりした変化)にはよく追従しますが、高い周波数の信号(急激な変化)には追従しにくくなります。
低周波領域では、ゲインはおよそ 0 dB となり、入力に対して出力がほぼ遅れなく追従します。
これは、ピカチュウが「ゆっくりとした放電命令」に対して素早く反応し、安定した電圧を出せる状態に対応しています。
一方で、高周波領域ではゲインが大きく減衰します。
非常に速い放電制御信号が入力されても、ピカチュウの電気袋には**時定数 $T$**という物理的な制約があるため、エネルギーが追いつかず出力が小さくなってしまいます。
そして、カットオフ周波数 $\omega_c = 1/T$ においてゲインは −3 dB となります。
ここがピカチュウの放電系が応答できる周波数の限界であり、これより速い変化では放電の威力が半分以下に減衰します。
このように、ピカチュウの放電は「低域を通し、高域を抑える」ローパス特性によって支配されているといえます。
結論:放電現象の数理モデルとしての意義
ピカチュウの「10万ボルト」は、単なる高電圧ではなく、時定数 $T$ によって支配される動的制御システムとして解析可能です。
- 時定数 $T$ が大きい: 応答が遅く、持続時間が長いが、素早い制御ができない(鈍い)。
- 時定数 $T$ が小さい: 応答が速く、瞬発力があるが、持続時間が短い(鋭い)。
この $T$ を調整することが、ピカチュウの**「電気技の制御レベル」に対応します。RC回路モデルは、この蓄積と減衰のトレードオフを制御工学の基本法則**に基づいて明確に説明します。
一次遅れ系の応用表
一次遅れ系のシミュレーション手法
| 項目 | MATLAB/Simulink | SPICEシミュレーション |
|---|---|---|
| 対象モデル | 連続時間伝達関数 $G(s) = \frac{1}{Ts+1}$ | RC回路(抵抗 $R$ とコンデンサ $C$) |
| 基本実装 | Transfer Fcn ブロック、State-Space ブロック、または Integrator を用いたブロック線図。 | 素子(R、C、電圧源)を接続した回路図。$T=RC$。 |
| 定式化の基礎 | 常微分方程式(ODE) $T\frac{dy}{dt} + y = u$ | 修正ノード解析(MNA) による連立微分方程式系。 |
| 解法の中核 | ODEソルバー(常微分方程式ソルバー)による数値積分。 | 数値積分手法とニュートン・ラフソン法(非線形素子を含む場合)。 |
| 代表的なソルバー | ode45(ルンゲ=クッタ法、標準)、ode15s(スティフ系用)、ode23t(台形則ベース)。 | 台形法(Trapezoidal Rule)、ギア法(Gear's Method)。 |
| 数学的手法 | ルンゲ=クッタ法などによる高精度な時間刻み調整(可変ステップ) 積分。 | 台形積分やギア積分を用いた固定または適応的な過渡解析。 |
| 離散化の関連 | ODEソルバーが内部で自動的に最適化された離散近似を実行。 | 数値積分の手法が、双一次変換(Tustin変換)などに類似した安定な離散化を与える。 |
| 用途 | 制御システム、機械・化学プラントなど広範な動特性の解析。 | 電子回路、半導体、電源回路など電気現象の厳密な過渡解析。 |
補足:数値積分手法の役割
MATLAB/SimulinkでもSPICEでも、連続時間システムの挙動を計算機で再現するために、**微分方程式を時間 $\Delta t$ ごとに近似的に解く「数値積分」**が必須です。
- ルンゲ=クッタ法 (ode45): Simulinkで標準的に使われ、高次のテイラー展開の精度を効率的に実現し、高い精度と安定性で非線形な現象にも対応します。
- 台形法 (SPICE): $\frac{dy}{dt}$ を台形の面積で近似する手法で、安定性が高く、特に回路シミュレーションで頻繁に用いられます。周波数領域での歪みが少ない(双一次変換と対応)という利点があります。
一次遅れ系伝達関数 $G(s) = \frac{K}{Ts+1}$ の構造を軸に、各手法がそのモデルの要素($K, T$)、動的な挙動($y(t)$)、または制御戦略にどのように関わるかを、学問分野ごとにさらに掘り下げて説明します。
一次遅れ系と8手法の詳細な関係性
1. 確率推論系:不確実性下のモデルと状態の取り扱い
| 手法名 | 一次遅れ系に対する詳細アプローチ |
|---|---|
| ベイズ推定 | 一次遅れ系を構成する時定数 $T$ やゲイン $K$ を事前確率分布で表現します。測定した入出力データ $D$ を得ることで、ベイズの定理を用いてこれらのパラメータの**事後確率分布 $P(K, T |
| カルマンフィルタ | 一次遅れ系の微分方程式 $\tau\frac{dy}{dt} + y = Ku$ を、離散時間での線形状態空間モデル $\mathbf{x}{k} = \mathbf{A}\mathbf{x}{k-1} + \mathbf{B}\mathbf{u}_k + \mathbf{w}_k$ に変換します(ここで $\mathbf{x}_k$ には出力 $y_k$ などが含まれます)。フィルタは、システムノイズ $\mathbf{w}_k$ と観測ノイズ $\mathbf{v}_k$ が存在する状況下で、最適な状態推定値 $\hat{\mathbf{x}}_k$ をリアルタイムで計算・予測します。これは、実機の制御において必須となるノイズ耐性のある動的システムの監視に応用されます。 |
2. 数値計算系:微分方程式の解法と空間的拡張
| 手法名 | 一次遅れ系に対する詳細アプローチ |
|---|---|
| 数値解析 | 一次遅れ系の基本式(1階の常微分方程式)は解析解を持ちますが、これが制御対象の非線形性や多変数化により複雑になった場合、オイラー法やルンゲ=クッタ法などの手法で時間軸上の離散化を行います。特に、制御シミュレーションでは、微小区間 $\Delta t$ ごとにシステムの次時刻の状態 $y(t+\Delta t)$ を反復的に計算し、一次遅れ系の**時間応答(ステップ応答など)**を求めます。 |
| 有限要素法 (FEM) | 一次遅れ系(集中定数系)のモデル化には直接的ではありませんが、熱伝導方程式や拡散方程式といった偏微分方程式を解くために用いられます。これらの偏微分方程式は、時間微分項と空間微分項を持ち、空間を要素に離散化(FEM)し、時間を数値解析で解くことでシミュレーションされます。その結果得られる応答は、多くの場合、一次遅れ的な特性(時間が経つにつれてゆっくりと定常値に収束する特性)を含みます。 |
3. 最適化系:パラメータ同定と制御性能の追求
| 手法名 | 一次遅れ系に対する詳細アプローチ |
|---|---|
| 最小二乗法 | 実験で得られた入出力データ ${(u_i, y_i)}_{i=1}^N$ を用い、伝達関数のモデル $G(s)$ のパラメータ $K, T$ を決定します。これは、「モデルが予測する出力」と「実際の観測出力」との残差二乗和(誤差関数)を最小化するパラメータを探す問題に帰着します。特に、この問題を線形回帰の形に変換することで、**閉じた形(解析解)**で最適な $K, T$ を効率的に求めることができます。 |
| 勾配降下法 | 最小二乗法で解析解が得られない非線形なシステム同定や、一次遅れ系を制御対象とする際の最適制御問題に適用されます。例えば、制御入力を決める制御則(コントローラ)のパラメータを学習させる際、性能指標(コスト関数)の勾配を計算し、その逆方向にパラメータを少しずつ更新します。これにより、一次遅れ系が目標値に最も効率的に追従するための制御パラメータを探索します。 |
4. 学習系:データ駆動型モデルと戦略の獲得
| 手法名 | 一次遅れ系に対する詳細アプローチ |
|---|---|
| 機械学習 | システム同定のアプローチをさらに進め、伝達関数 $G(s)$ のようなホワイトボックスモデルを仮定せず、入出力データから直接時系列予測モデルを構築します。例えば、リカレントニューラルネットワーク (RNN) や時系列特化型のモデルを使い、過去の入力 $u(t)$ と出力 $y(t)$ から次の出力 $y(t+\Delta t)$ を予測します。これは、モデル化が困難な非線形な一次遅れ系(例:ヒステリシスを含む系)の挙動を再現するのに適しています。 |
| 強化学習 | 一次遅れ系を「環境」とし、制御対象の状態 $y(t)$ を観測しながら、制御入力 $u(t)$(行動)を決定するエージェントを学習させます。エージェントは、目標値に速く正確に到達できた場合に報酬を得るように設計され、試行錯誤を通じて最適な制御戦略(ポリシー)を獲得します。これは、モデルの知識なしに、目標追従や外乱抑制など、一次遅れ系に対する高度な自律制御を実現する可能性を秘めています。 |
補足:一次遅れ系から制御工学への展開
一次遅れ系は、制御工学において以下のように応用が発展します。
- 遅れ要素の表現: 時定数 $T$ を持つ一次遅れ系は、信号のエネルギー蓄積による遅延やフィルタリング効果を最もシンプルに表現し、あらゆる複雑なシステム解析の基本ブロックとして使われます。
- PID制御: 実際の制御器であるPID制御(比例・積分・微分)の設計では、一次遅れ系(またはそれに無駄時間要素を加えた系)が制御対象のモデルとして頻繁に使用され、ゲイン余裕や位相余裕といった安定性の指標を計算する基礎となります。
- モデル予測制御 (MPC): MPCのような高度な制御手法では、一次遅れ系のようなシンプルな動的モデルを使って将来のシステムの挙動を予測し、その予測に基づいて最適化手法(勾配降下法など)を用いて最適な制御入力をリアルタイムで計算します。
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# --------------------------
# Parameters / ピカチュウ放電モデル設定
# --------------------------
V0 = 100000 # 入力電圧 [Volt] (10万ボルト)
T = 0.05 # 時定数 [s](ピカチュウの放電速度)
K = 1.0 # ゲイン
t = np.linspace(0, 0.25, 500)
# --------------------------
# Step Response / 放電過程(RC放電)
# --------------------------
Vout = V0 * (1 - np.exp(-t/T))
plt.figure()
plt.plot(t, Vout, label="Pikachu Discharge Voltage Vout(t)")
plt.axhline(V0, color='gray', linestyle='--', linewidth=0.8, label="Steady-state (100000 V)")
plt.axvline(T, color='red', linestyle='--', linewidth=0.8, label=f"t = T = {T}s (63.2%)")
plt.title("Pikachu's 100000 Volt Discharge (RC Model)")
plt.xlabel("Time [s]")
plt.ylabel("Voltage [V]")
plt.legend()
plt.grid(True)
# --------------------------
# Frequency Response / 放電系の周波数応答
# --------------------------
system = signal.TransferFunction([K], [T, 1])
omega = np.logspace(1, 6, 500) # 10〜1MHz
w, mag, phase = signal.bode(system, omega)
plt.figure()
plt.subplot(2, 1, 1)
plt.semilogx(w, mag)
plt.title("Bode Plot of Pikachu's 100000 Volt System")
plt.ylabel("Magnitude [dB]")
plt.axvline(1/T, color='red', linestyle='--', linewidth=0.8, label="ω = 1/T (cutoff)")
plt.legend()
plt.grid(True, which='both')
plt.subplot(2, 1, 2)
plt.semilogx(w, phase)
plt.ylabel("Phase [deg]")
plt.xlabel("Angular Frequency ω [rad/s]")
plt.axvline(1/T, color='red', linestyle='--', linewidth=0.8)
plt.grid(True, which='both')
# --------------------------
# Energy Model / ピカチュウ放電エネルギー(近似)
# --------------------------
C = 1e-3 # 仮想コンデンサ [F]
E = 0.5 * C * (V0 ** 2) # E = 1/2 C V^2
print(f"ピカチュウ放電エネルギー推定値: E = {E:.2e} [J]")
# --------------------------
# コメント / 物理的意味
# --------------------------
"""
ピカチュウの10万ボルト = RC放電過程
- 入力: 神経系の刺激による放電命令 (Vin)
- 出力: 電気袋に蓄えた電圧 (Vout)
- 時定数 T = R*C が放電速度を決める
- 放電エネルギー E = 0.5*C*V^2 ≈ 5 J(C=1mF時)
→ 数ジュール規模の電撃、短時間に放出すると致命的な衝撃を与える
- 周波数応答では ω=1/T を境に出力が−3dB減衰(制御工学的意味)
"""
plt.tight_layout()
plt.show()
---