位置づけ
本記事はPython機械学習プログラミング 達人データサイエンティストによる理論と実装の16章を読んだ時のメモです。
この記事の続きです。
Long Short-Term Memory(LSTM)
RNNの記事の中で、時間方向に長いネットワーク展開がある場合に勾配消失/爆発問題が起こりやすいことを確認しました。勾配消失/爆発問題の解決策の一つとしてLSTMを見ていきます。
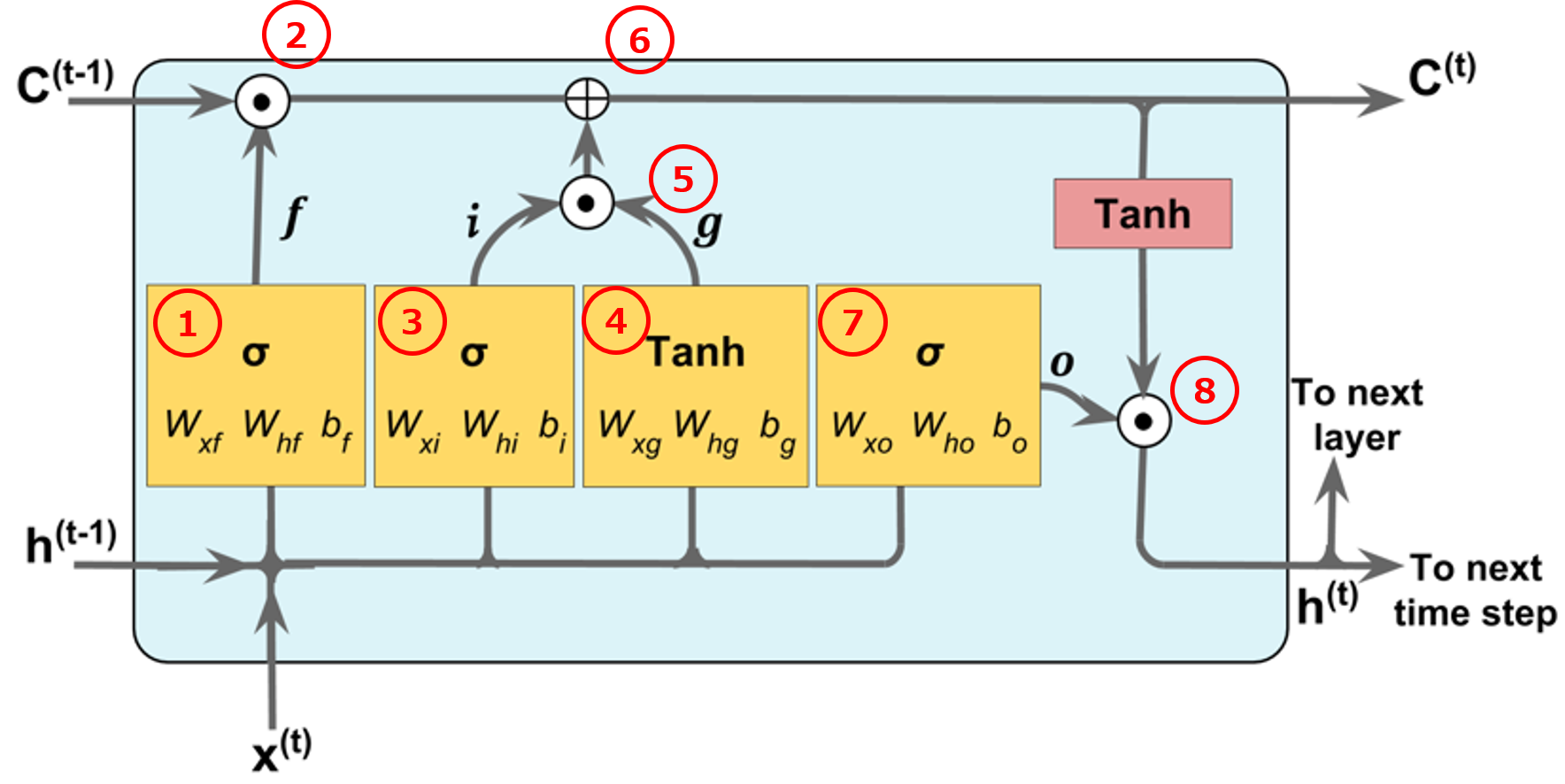
$$\style{align: center; font-family: "Helvetica Neue",Helvetica,"ヒラギノ角ゴ ProN W3","Hiragino Kaku Gothic ProN","メイリオ",Meiryo,sans-serif}{\text{Fig.1 LSTMセルの構造}}$$
LSTMはRNNの中間層のユニットをFig.1で示されるLSTMセルで置き換えた構造を持っています。LSTMの中間層の記憶セルには、前の層からの出力と(Fig.1は2層ネットワークなので入力$\boldsymbol{x}^{(t)}$)、一つ前の時間ステップ$t-1$からの出力$\boldsymbol{h}^{(t-1)}$と記憶$\boldsymbol{C}^{(t-1)}$が入力されます。RNNのように$t-1$以前のすべての情報を保持しようとするのではなく、保持すべき情報のみを次の時間ステップ、次の層へと流してゆきます。これを実現するために以下の3つのゲートを組み合わせて使います。
忘却ゲート
忘却ゲートでは、一つ前の時間ステップから渡された記憶(セルの状態)のうちどれだけの記憶を、次の時間ステップに渡すかを調整します。(Fig.1の赤丸1)
\begin{eqnarray*}
\boldsymbol{f}_t = \sigma \left( \boldsymbol{W}_{xf}\boldsymbol{x}^{(t)} + \boldsymbol{W}_{hf}\boldsymbol{h}^{(t-1)} + \boldsymbol{b}_f\right)
\end{eqnarray*}
$\sigma(\cdot)$はシグモイド関数であり、出力を$[0,1]$に制限します。この出力が$1$に近ければ情報を多く保持し、$0$に近ければ情報を捨てて(忘却して)しまいます。
時間ステップ$t-1$から渡される記憶(セルの状態)を$\boldsymbol{C}^{(t-1)}$とすれば、現在の時間ステップで保持される過去の記憶は、次のように計算されます。(Fig.1の赤丸2)
\begin{eqnarray*}
\boldsymbol{C}^{(t-1)} \odot \boldsymbol{f}_t
\end{eqnarray*}
ここで、演算子$\odot$は成分ごとの積を表します。
入力ゲート
入力ゲートでは、一つ前の時間ステップから渡される情報$\boldsymbol{h}^{(t-1)}$と現在の時間ステップで入力される情報$\boldsymbol{x}^{(t)}$のうち、どれだけの情報をLSTMの記憶セルに受容するかをコントロールします。
入力ゲートは、次の式で計算されます。(Fig.1の赤丸3)
\begin{eqnarray*}
\boldsymbol{i}_t = \sigma \left( \boldsymbol{W}_{xi}\boldsymbol{x}^{(t)} + \boldsymbol{W}_{hi}\boldsymbol{h}^{(t-1)} + \boldsymbol{b}_i\right)
\end{eqnarray*}
忘却ゲート同様に、出力が$[0,1]$に制限され、$1$に近ければ多くの情報をLSTM記憶セルに取り込み、$0$に近ければ新しい情報をほとんど受け入れないことになります。
入力ゲートを通過しようとする情報は次の式で計算され、(Fig.1の赤丸4)
\begin{eqnarray*}
\boldsymbol{g}_t = \mathrm{tanh} \left( \boldsymbol{W}_{xg}\boldsymbol{x}^{(t)} + \boldsymbol{W}_{hg}\boldsymbol{h}^{(t-1)} + \boldsymbol{b}_g\right)
\end{eqnarray*}
この出力値が入力ゲートを通過した後の値は、(Fig.1の赤丸5)
\begin{eqnarray*}
\boldsymbol{i}_t \odot \boldsymbol{g}_t
\end{eqnarray*}
と計算されます。
以上より、現在の時間ステップ$t$でのLSTM記憶セルが持つ記憶(セルの状態)は、時間ステップ$t-1$から受け継いだ記憶と、時間ステップ$t$で新たに得た情報の和で表現され、次のように記述されます。(Fig.1の赤丸6)
\begin{eqnarray*}
\boldsymbol{C}^{(t)} = \left( \boldsymbol{C}^{(t-1)} \odot \boldsymbol{f}_t \right) \oplus \left(\boldsymbol{i}_t \odot \boldsymbol{g}_t \right)
\end{eqnarray*}
この値が時間ステップ$t$で保持していた記憶として、次の時間ステップ$t+1$のLSTM記憶セルへと引き継がれます。
出力ゲート
出力ゲートは、LSTM記憶セルが保持している情報のうち、どれだけの量を次の層と次の時間ステップに引き渡すかをコントロールします。忘却ゲートと入力ゲートの存在で、記憶セル内に保持しておくべき情報は$\boldsymbol{C}^{(t)}$として保計算できているので、この情報を次の層へと引き継いでいきます。言い換えれば、$\boldsymbol{h}^{(t-1)}$と$\boldsymbol{x}^{(t)}$から無駄な部分をそぎ落とした情報を中間層の出力とします。出力ゲートの開度と、そこを通過した情報は次のように計算されます。(Fig.1の赤丸7と赤丸8)
\boldsymbol{o}_t = \sigma \left( \boldsymbol{W}_{xo}\boldsymbol{x}^{(t)} + \boldsymbol{W}_{ho}\boldsymbol{h}^{(t-1)} + \boldsymbol{b}_o\right)\\
\boldsymbol{h}^{(t)} = \boldsymbol{o}_t \odot \mathrm{tanh} \left( \boldsymbol{C}^{(t)}\right)
忘却ゲートと入六ゲート同様に、シグモイド関数で出力を$[0,1]$に制限することでゲートの開度を表現しています。
LSTMが記憶を保持する仕組み
ここまで、LSTMセルの各ゲートの役割を説明してきました。各ゲートの動きによって記憶セルが記憶を保持する仕組みを理解するために、2つの簡単な思考実験をしてみます。
1.入力ゲートが完全に閉じた状態(0)で、忘却ゲートが完全に開いた状態(1)
入力ゲートが完全に閉じているので時間ステップ$t-1$からの出力$\boldsymbol{h}^{(t-1)}$と一つ前の層からの出力$\boldsymbol{x}^{(t)}$が記憶に加わることはありません。つまり、新しい情報は一切受け付けず過去の記憶だけをそのまま出力するモデルとなります。
2.入力ゲートが完全に開いた状態(1)で、忘却ゲートが完全に閉じた状態(0)
忘却ゲートが完全に閉じているので過去の記憶は一切保持されません。入力ゲートは全開なので時間ステップ$t-1$からの出力$\boldsymbol{h}^{(t-1)}$と一つ前の層からの出力$\boldsymbol{x}^{(t)}$の情報すべてが新しい記憶として次の時間ステップに引き継がれます。ちょうどRNNと同じモデルになります。
上記2つの思考実験からわかる通り、必要な情報は記憶し不要な情報は忘却して、効率よく情報を長期間保持しておくためには各ゲートが入力データに合わせて調和的に開閉する必要があります。データに合わせて各ゲートがうまく開閉するようにそれぞれのの重みパラメータが学習されます。
学習は通常のRNNと同様に誤差逆伝搬法を用います。(更新式の導出はまた今度書きます・・・)
LSTMセルの導入でなぜ勾配爆発/消失が抑制されるのか
勾配消失/爆発問題への対応策としてLSTMは導入されたのでした。実際にLSMT記憶セルがどのように機能するのか見てみましょう。
誤差逆伝搬法による学習においても、出力ゲートと入力ゲートによって、ネットワークを伝搬していく誤差の大きさが制御されます。時間ステップ$t+1$と第$(l+1)$層から流入する誤差は出力ゲートによって減衰され(誤差にも出力ゲートの$[0,1]$が乗算される)、記憶セルに流入する誤差の大きさがコントロールされます。仮に大きな誤差が流入したとしても、$t-1$と第$(l-1)$層に出力される際には、入力ゲートによってその量が調整され、次のユニットへと大きな誤差が流れ込むことを防止します。
参考文献
講談社 MLPシリーズ 深層学習 Chapter7
LSTM論文