位置づけ
本記事はPython機械学習プログラミング 達人データサイエンティストによる理論と実装の16章を読んだ時のメモです。
系列データ
系列データ以外のデータ(irisデータセットなど)は各データインスタンスは互いに独立に生成される、つまり、独立同分布(independent and identicalll distributed : i.i.d)に従ってデータが生成されているという仮定のもとで議論を進めてきました。今回取り扱うのはこの仮定が適用できない系列データです。
系列データの取り扱いにおいては「データが生成される順番に意味がある」と考えて、データの並びから意味を見出すことを行います。
RNNによる系列データのモデリング
時系列データのモデリングに置いて重要なことは「どのようにして過去のパターンを記憶し、その記憶から予測を行うか」ということです。RNNにおいては、Fig.1が示すように一つの順伝搬ネットワークを時間方向に展開し(unfoldし)、中間層の出力を次の時間ステップの中間層へと入力することによりこれを実現しようとしています。$t=0$の情報が$t=1$に伝わり、$t=0$の情報も含んだ$t=1$の情報が$t=2$のネットワークに伝わり・・・最終的に$t=T$まで伝わることになります。理論上は$t = 0, 1, \cdots, t-1$までのすべての情報が$t=t$における$\boldsymbol{h}^{(t)}$に含まれていることになります。しかし実際には、高々10ステップ程前の情報までしか保持されていないようです。
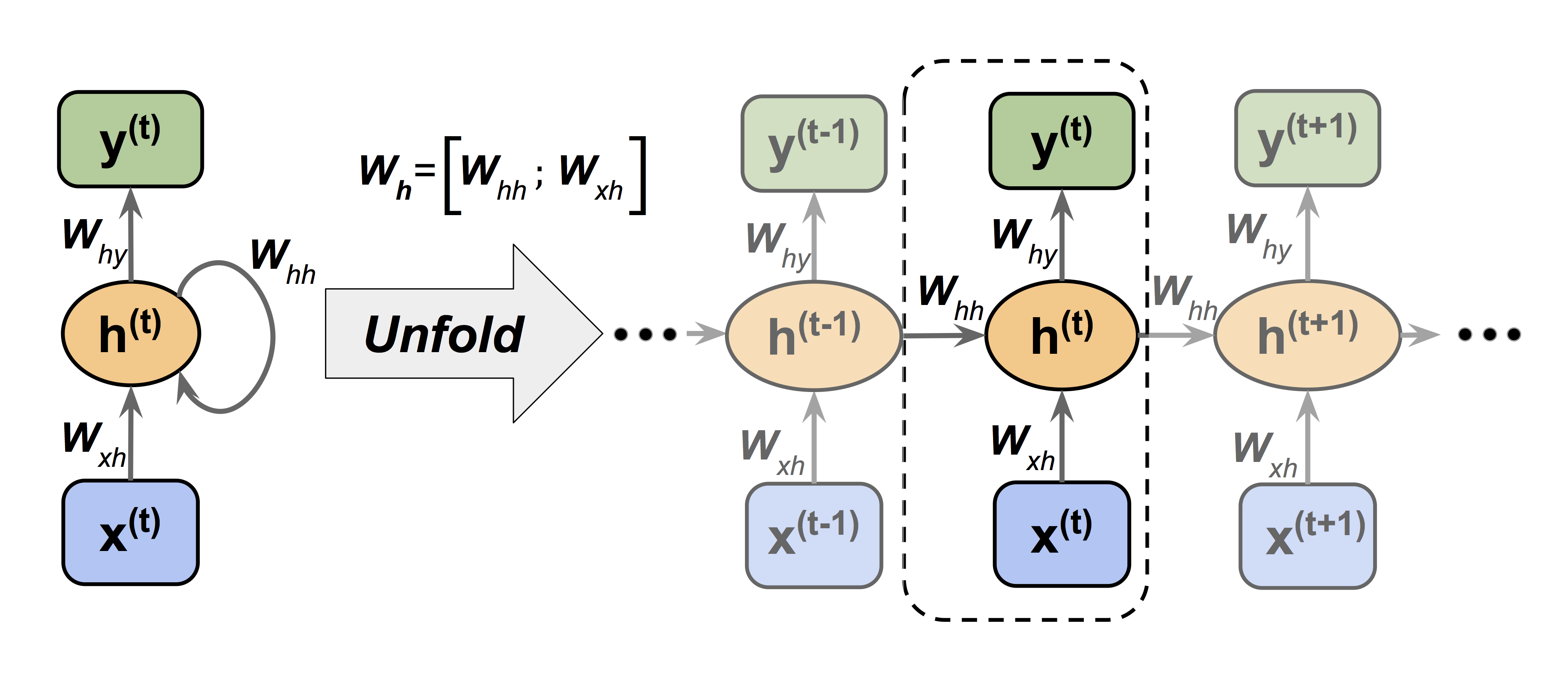
$$\style{align: center; font-family: "Helvetica Neue",Helvetica,"ヒラギノ角ゴ ProN W3","Hiragino Kaku Gothic ProN","メイリオ",Meiryo,sans-serif}{\text{Fig.1 RNNの構造}}$$
順伝搬計算の記述
Fig.1で表現されるRNNの順伝搬計算の式を導いてみましょう。
ここで注意すべきは、ユニット結合の重み$\boldsymbol{W}_{xh}$と$\boldsymbol{W}_{hh}$はすべての時間ステップにおいて共有されていることです。unfoldした図を見ると各時間ステップ$t$で別の重みが使用されているように考えてしまいがちです。
入力次元数を$M$とし、中間層のユニット数を$H$、出力次元を$D$とすれば、各パラメータ行列や変数の次元は、$\boldsymbol{x}^{(t)} \in \mathbb{R}^{M}$, $\boldsymbol{h}^{(t)} \in \mathbb{R}^{H}$, $\boldsymbol{y}^{(t)} \in \mathbb{R}^{D}$, $\boldsymbol{W}_{xh} \in \mathbb{R}^{H \times M}$, $\boldsymbol{W}_{hh} \in \mathbb{R}^{H \times H}$, $\boldsymbol{W}_{hy} \in \mathbb{R}^{D \times M}$となります。
この条件下で順伝搬計算は次のように記述されます。
\boldsymbol{z}^{(t)}_{h}=\boldsymbol{W}_{xh}\boldsymbol{x}^{(t)} + \boldsymbol{W}_{hh}\boldsymbol{h}^{(t-1)} + \boldsymbol{b}_{h}\\
\boldsymbol{h}^{(t)} = \phi_{h} \left( \boldsymbol{z}^{(t)}_{h} \right)\\
\boldsymbol{y}^{(t)} = \phi \left( \boldsymbol{W}_{hy}\boldsymbol{h}^{(t)} + \boldsymbol{b}_{y}\right)
尚、今回は中間層が1層だけですが、以下のように同じ枠組みで2層以上に拡張することも可能です。(各変数・重みの右肩に層を特定する$(l)$を付けるだけ)
\boldsymbol{z}^{(l,t)}_{h}=\boldsymbol{W}^{(l)}_{xh}\boldsymbol{h}^{(l-1,t)} + \boldsymbol{W}^{(l)}_{hh}\boldsymbol{h}^{(t-1)} + \boldsymbol{b}^{(l)}_{h}\\
\boldsymbol{h}^{(l,t)} = \phi_{h} \left( \boldsymbol{z}^{(l,t)}_{h} \right)\\
\boldsymbol{y}^{(t)} = \phi \left( \boldsymbol{W}_{hy}\boldsymbol{h}^{(L-1,t)} + \boldsymbol{b}^{(L)}_{y}\right)
最終層での活性化関数を$\phi (\cdot)$としていますが、回帰のタスクであれば恒等写像となります。
逆伝搬計算の記述 Back-Propagation Through Time (BPTT)
BPTT法を用いて誤差逆伝搬による層方向の各重み成分$w^{(l)}_{ji}$と時間方向の各重み成分$w^{(l)}_{jj^\prime}$の更新式を導きます。BPTT法では、RNNを時間方向にunfoldしたネットワークを、中間層間に接続があるひとつの全結合DNNと見なし、誤差逆伝搬計算を行います。順伝搬計算では2層ネットワークを前提とした定式化をしていましたが、ここでは任意の層数のネットワークを前提として定式化を試みます。(その方がわかりやすいです。)
重みの更新式は、
w^{(l), \mathrm{new}}_{ji}=w^{(l), \mathrm{old}}_{ji} - \eta \frac{\partial L}{\partial w^{(l)}_{ji}}\\
w^{(l), \mathrm{new}}_{jj^\prime}=w^{(l), \mathrm{old}}_{jj^\prime} - \eta \frac{\partial L}{\partial w^{(l)}_{jj^\prime}}\\
L = \sum^{T}_{t=1} L^{(t)}
と表現され、重みは時間ステップ間で不変なので、誤差逆伝搬計算では$\frac{\partial L}{\partial w^{(l)}_{ji}}$と$\frac{\partial L}{\partial w^{(l)}_{jj^\prime}}$を求めることが目標となります。尚、$L^{(t)}$は時間ステップ$t$における予測誤差です。
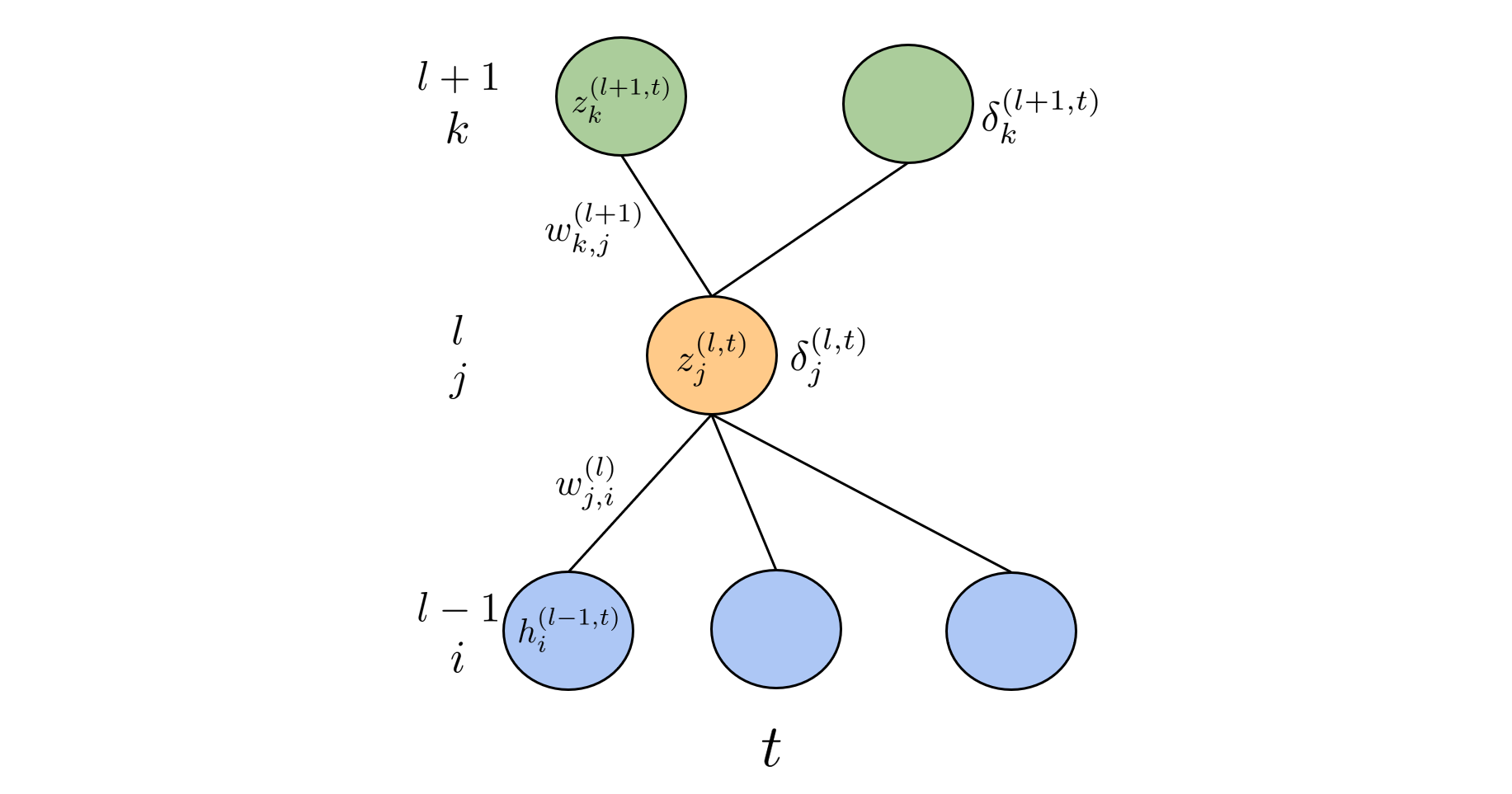
式の導出にあたり、下図のイメージが大切ですので頭に思い浮かべておいてください。誤差逆伝搬計算は添え字の嵐で、添え字の定義を頭に叩き込んでおかないと計算の見通しが悪くなります。
第$(l)$層に注目した時、第$(l)$層のユニットを$j$で参照し、第$(l-1)$層と第$(l+1)$層のユニットをそれぞれ$i$と$k$で参照します。時間ステップ$t$は上付き添え字で参照します。また重み成分$w^{(l)}_{ji}$の下付き添え字は第$(l)$層のユニット$j$への第$(l-1)$層のユニット$i$からの接続を表しています。時間ステップ$t$をまたいだ接続は、$t+1$と$t-1$の第$(l)$層のユニットを$j^{\prime}$で参照します。この場合も接続先のユニットを下付き添え字の前の文字で参照し、接続元を後の文字で参照します。
 !
!
$$\style{align: center; font-family: "Helvetica Neue",Helvetica,"ヒラギノ角ゴ ProN W3","Hiragino Kaku Gothic ProN","メイリオ",Meiryo,sans-serif}{\text{Fig.2 層方向の伝搬計算の添え字}}$$
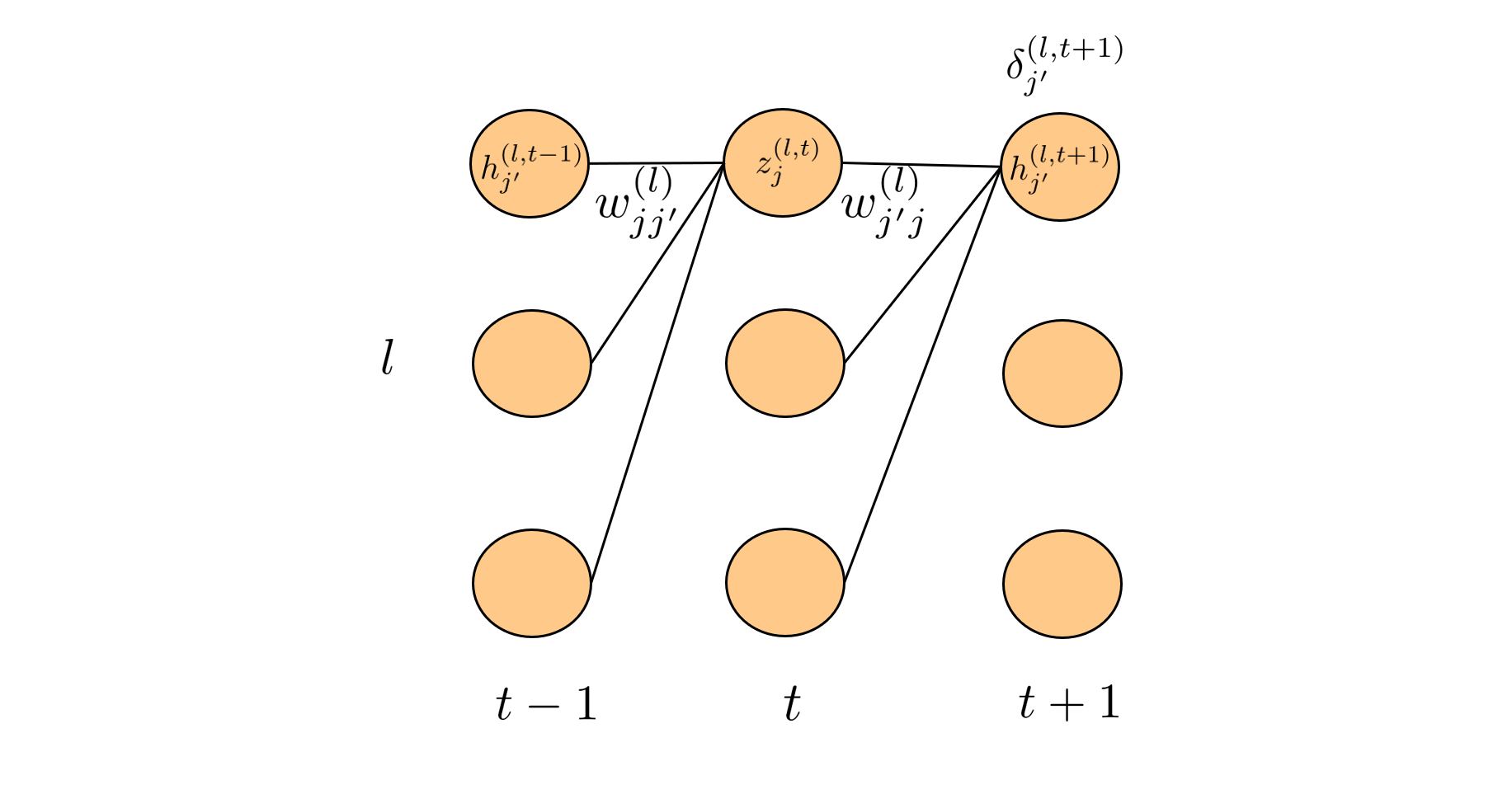
$$\style{align: center; font-family: "Helvetica Neue",Helvetica,"ヒラギノ角ゴ ProN W3","Hiragino Kaku Gothic ProN","メイリオ",Meiryo,sans-serif}{\text{Fig.3 時間方向の伝搬計算の添え字}}$$
求めたい2つの勾配に連鎖律を適用してみると、
\begin{eqnarray*}
\frac{\partial L}{\partial w^{(l)}_{ji}} &=& \frac{\partial L}{\partial z^{(l, t)}_j} \frac{\partial z^{(l, t)}_j}{\partial w^{(l)}_{ji}}\\
&=&\delta^{(l,t)}_{j}\frac{\partial}{\partial w^{(l)}_{ji}} \left\{ \sum_i w^{(l)}_{ji}h^{(l-1, t)}_i + \sum_{j^\prime}w_{jj^\prime}h^{(l, t-1)}_{j^\prime}\right\}\\
&=&\delta^{(l,t)}_{j}h^{(l-1, t)}_i
\end{eqnarray*}
\begin{eqnarray*}
\frac{\partial L}{\partial w^{(l)}_{jj^\prime}} &=& \frac{\partial L}{\partial z^{(l, t)}_j} \frac{\partial z^{(l, t)}_j}{\partial w^{(l)}_{jj^\prime}}\\
&=&\delta^{(l,t)}_{j}\frac{\partial}{\partial w^{(l)}_{jj^\prime}} \left\{ \sum_i w^{(l)}_{ji}h^{(l-1, t)}_i + \sum_{j^\prime}w_{jj^\prime}h^{(l, t-1)}_{j^\prime}\right\}\\
&=&\delta^{(l,t)}_{j}h^{(l, t-1)}_{j^\prime}
\end{eqnarray*}
となります。ただし、以下のように置き換えました。
\begin{eqnarray*}
\frac{\partial L}{\partial z^{(l, t)}_j} =\delta^{(l,t)}_{j}
\end{eqnarray*}
$\delta^{(l,t)}_{j}$は誤差逆伝搬の過程で時間ステップ$t$で第$l$層に流入する誤差であり、これが計算できれば求めたい二つの勾配が計算できることがわかります。
BPTT法がRNNを時間方向に展開して全結合DNNのように扱うことを思い出すと、Fig.4が示すように、時間ステップ$t$の第$(l)$層に流入する誤差は時間ステップ$t$の第$(l+1)$層から流入する誤差と、時間ステップ$t+1$の第$(l)$から流入する誤差の和で表現されます。
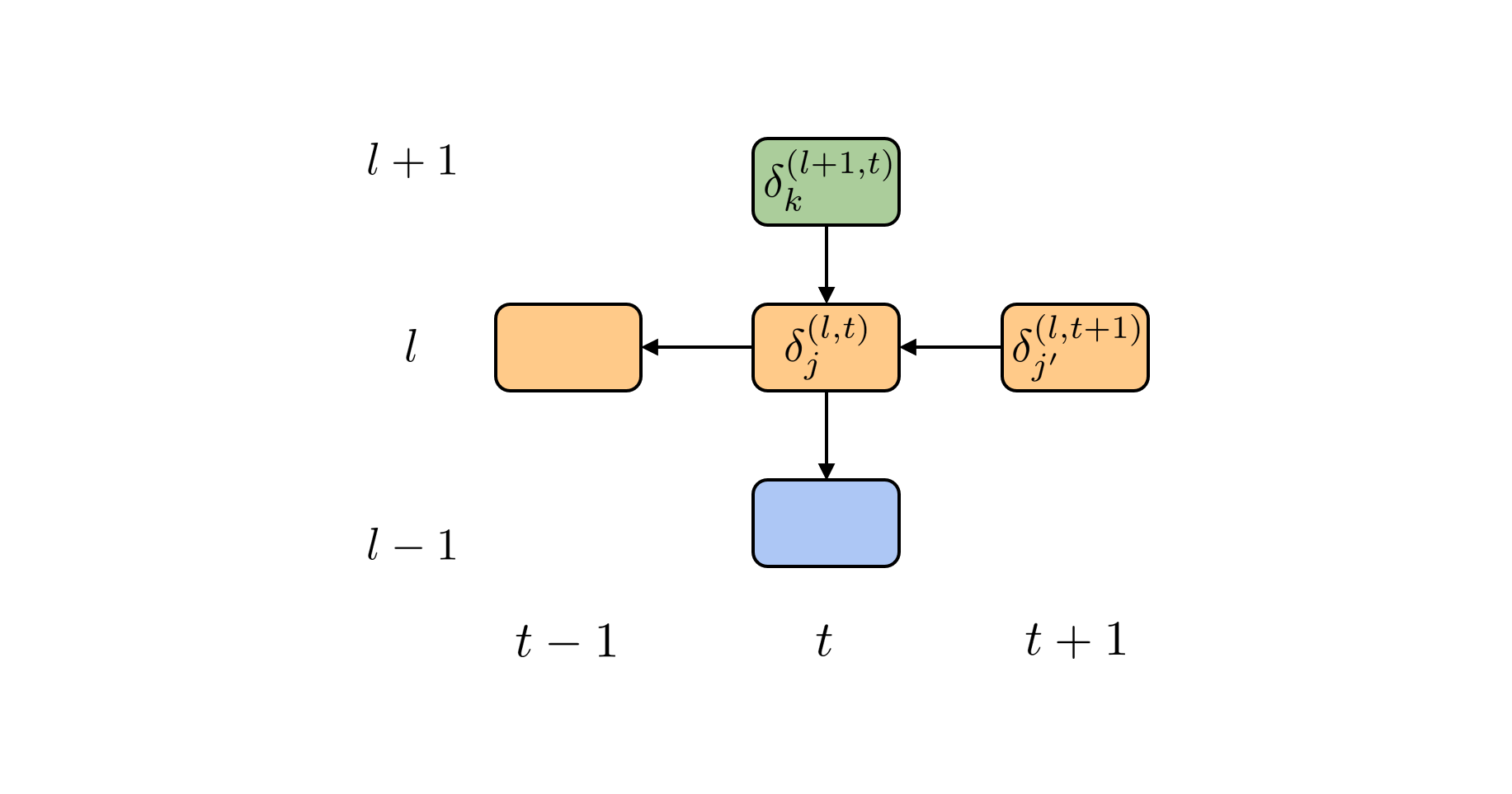
$$\style{align: center; font-family: "Helvetica Neue",Helvetica,"ヒラギノ角ゴ ProN W3","Hiragino Kaku Gothic ProN","メイリオ",Meiryo,sans-serif}{\text{Fig.4 誤差の流入}}$$
層方向に伝搬する誤差は、通常のニューラルネットワークの誤差逆伝搬を導出したときと同じようにして計算できます。具体的には、Fig.2から、第$(l)$層のユニット$j$への総入力$z^{(l, t)}_j$の変化は、その活性$h^{(l, t)}_j$を通じて、第$(l+1)$層のすべてのユニットの総入力へと影響を与えることがわかります。時間方向に伝搬する誤差も同様にして$h^{(l, t)}_j$を通じて、時間ステップ$t+1$の第$(l)$層のすべてのユニットの総入力へと影響を与えます。
すなわち、
\begin{eqnarray*}
\delta^{(l,t)}_j =
\frac{\partial L}{\partial z^{(l, t)}_j} &=&\sum_{k} \frac{\partial L^{(t)}}{\partial z^{(l+1, t)}_{k}}\frac{\partial z^{(l+1, t)}_{k}}{\partial z^{(l, t)}_j} + \sum_{j^\prime} \frac{\partial L}{\partial z^{(l, t+1)}_{j^\prime}}\frac{\partial z^{(l, t+1)}_{j^\prime}}{\partial z^{(l, t)}_j}\\
&=&\sum_{k}\delta^{(l+1, t)}_{k}\frac{\partial}{\partial z^{(l, t)}_j}\left\{ \sum_{j} w^{(l+1)}_{kj}h^{(l, t)}_j \right\}
+\sum_{j^\prime}\delta^{(l, t+1)}_{j^\prime}\frac{\partial}{\partial z^{(l, t)}_j}\left\{ \sum_{j} w^{(l)}_{j^\prime j}h^{(l, t)}_{j}\right\}\\
&=&\left\{ \sum_{k}\delta^{(l+1, t)}_{k}w^{(l+1)}_{kj} + \sum_{j^\prime}w^{(l)}_{j^\prime j}\delta^{(l, t+1)}_{j^\prime}\right\}\phi^{\prime} \left( z^{(l, t)}_j\right)\tag{*}
\end{eqnarray*}
と記述されます。
この式が意味しているのは、時間ステップ$t$での第$(l)$層へ流入する誤差は第$(l+1)$層での誤差と時間ステップ$t+1$での誤差から計算できるということです。全結合DNNにおける誤差逆伝搬法と同様に時間ステップ$t=T$における最終層での誤差(回帰であれば2乗誤差、多クラス分類であれば交差エントロピー誤差)を第$(L-1)$層へと伝搬させ、第$(L-1)$で計算された誤差を第$(L-2)$層と、時間ステップ$T-1$へと伝搬させ、これを再帰的に繰り返せばすべての層のすべてのユニットに流入する誤差を計算することができます。ただし、時間ステップ$T$に流入する時間方向の誤差は0として扱います。
各重み成分の更新式は、$\delta^{(l,t)}_j$が計算できれば計算できることをすでに確認しました。順伝搬で最終層の誤差を計算し、逆伝搬によってその誤差から重みの更新式を計算することができます。これでRNNを学習することができるようになりました。
RNNの問題点
RNNの学習でいつもつきまとう問題は勾配消失と勾配爆発の問題です。RNNの学習では全結合DNNの学習と比較して、頻繁に勾配爆発/消失が起こってしまいます。それがなぜなのか説明します。
$\delta^{(l, t)}_j$の計算式$(*)$を見ると時間ステップ$t+1$から流入してくる誤差に重み$w^{(l)}_{j^\prime j}$と勾配$\phi^{\prime}()$が乗算されて次の時間ステップ$t-1$へと流入していきます。時間ステップ$t-1$でも再度重みと勾配が乗算されて次の時間ステップへと渡されます。つまり、時間ステップが$1$に近いところまで誤差が伝搬されたときにはすでに相当回数の重みと勾配が乗算されています。Fig.5が示すように重みと勾配が乗算された値の絶対値が$1$より小さければ時間ステップ$1$付近の誤差はほとんど$0$となり重み更新式の勾配は$0$となってしまいます。勾配がないので重みの学習はできません。これが勾配消失です。
一方、重みと勾配の積が$1$より大きければ時間ステップ$1$付近の誤差はとてつもなく大きな値となり、更新式の勾配も大きな値となり、重みは大きな値をとりながら振動します。次の逆伝搬計算で、さらに大きな重みが乗算されることになり、悪循環が止まることなく発散してしまいます。これが勾配爆発です。
これを踏まえると誤差に重みと勾配が乗算される回数が多いほど、勾配消失/爆発の問題が起こりやすくなることがわかります。$(*)$式の第一項にも層方向の誤差の伝搬として同じ形式の式が含まれていますが、この項での重みと勾配の乗算回数は$L-1$回であり、これは、典型的なRNNにおける時間方向の長さと比べてとても少ない回数です。全結合DNNにおいても層が深くなるにつれて勾配爆発/消失が起こりやすくなりますが、時間方向に長く展開されるRNNの方がこのリスクは大きくなります。
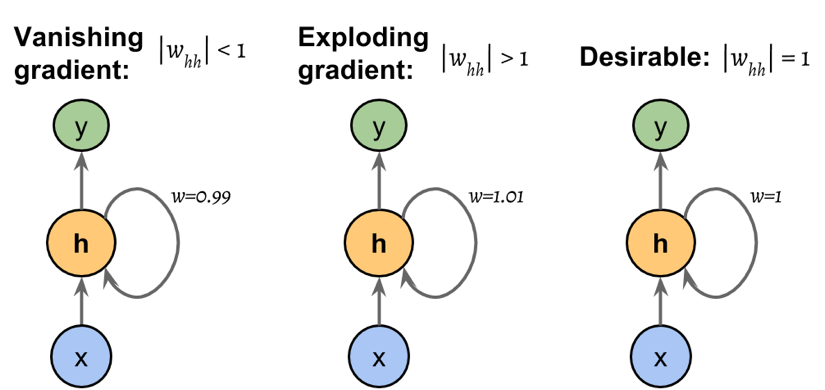
$$\style{align: center; font-family: "Helvetica Neue",Helvetica,"ヒラギノ角ゴ ProN W3","Hiragino Kaku Gothic ProN","メイリオ",Meiryo,sans-serif}{\text{Fig.5 勾配爆発/消失のイメージ図}}$$
(注意)上のポンチ絵では重みの絶対値によって、勾配消失/爆発が起こるように描かれていますが、厳密には重みと勾配の積の絶対値が$1$である必要があります。
勾配消失/爆発の問題にどう対処する?
勾配消失/爆発に対してロバストな学習をするために、活性化関数にtanhやsigmoidなどの飽和関数を用いたり、活性化後の出力の大きさを制御するためにバッチ正規化を適用したり、勾配のクリッピングでナイーブに勾配爆発を防止したり、いろいろな方法があります。また中間層間の時間方向の伝搬にLSTMセルを挟むことも有効です。
参考文献
講談社 MLPシリーズ 深層学習 Chapter4, Chapter7
LSTM論文