ニューラルネットワークの基礎知識 - 1

概要

ニューラルネットワークの基礎を理解するために、隠れ層ない状態でのネットワークを構築します。フレームワークを使わずにスクラッチから作ります。
以下を通じて、ニューラルネットワークへの理解深める事が本記事の趣旨です。
① weight
② bias
③ feedforward
④ cost
⑤ backpropagation

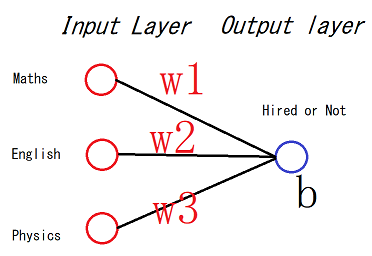
今回作成するネットワークは、**入力層で３つのニューロン（または、ノード）**を持ち、出力層では、一つのニューロンを持ちます。

入力層の３つのニューロンは以下の情報をもちます。
① １番目ニューロン：数学の結果（合格・不合格）
② ２番目ニューロン：英語の結果（合格・不合格）
③ ３番目ニューロン：物理の結果（合格・不合格）

出力層のニューロンは仕事を見つかるかどうかの情報を持ちます。出力層のニューロンの値が１の場合は仕事が見つかる、０の場合は見つからない意味合いになります。

各項目の説明

WEIGHT

Weight(重み)とは、ニューロン間の接続の強さを表します。ニューロン1からニューロン2への重みの大きさが大きい場合、ニューロン1がニューロン2に対する影響が大きいことを意味します。 重みがゼロに近い場合、この入力を変更しても出力は変更されません。重みは、入力が出力に与える影響を決定します。

BIAS

バイアスとは、inputとweightの様なニューロンへの入力値です。この値があることで、特定のデータが学習モデルに丁度いい感じでフィットします。
つまり、いい結果を推測するモデルを作るために必要となる定数と思ってください。

FEED FORWARD

Feed Forwardとは、情報が入力層のニューロンから隠れ層のニューロン（存在する場合）を介して出力層のニューロンに向かって一方向にのみ移動する仕組みです。
分かりやすいGIFを見つけたので共有します。

下記の数式を用いて入力値に対する答えを計算します。「sigmoid」とは活性化関数です。今回はsigmoidを使いますが、それ以外にtanh、relu、等があります。計算方法は以下のようになります。

推測結果' = input x weight + bias
推測結果 = sigmoid(推測結果')

先頭の画像の場合は、

推測結果' = Maths x w1 + English * w2 + Physics * w3 + b

Maths, English, Physics とは入力値であり決まってあります。w1,w2,w3,bは学習時に計算します。

COST

Feed Forwardで計算した結果と実際の結果の差の事をCOSTを言います。ERRORを言ったりすることもあります。COSTとは、単純に以下のように計算することもできますが、

COST = 予測値 - 実際の値

**MSE(Mean Squared Error平均二乗誤差)という手法を採用する事が多い。いいモデルを作るためには、このCOSTの値を少なくする必要があります。ニューラルネットワークでは入力値を変えることができないので、変えることができるのがweightとbiasのみです。なので、COSTを少なくするためには、weightとbiasを調整するしかありません。また、この調整の方法も色々ありますが、よく使う手法としてGradient　Descent(勾配降下)**があります。

BACKPROPAGATION

Backpropagationとは、後方の層で計算したweight、biasを前の層のニューロンに反映する仕組みです。
Backとは後ろの意味です。
propagationとは伝達する意味です。
この仕組みがあるからこそニューラルネットワークが賢くなります。
基礎なので具体的に書きませんが、weightとbiasの調整は以下の数式で行います。

Let's Code

学習データの用意

数学、英語、物理の合格状態によってある仕事がみつかったかどうかという仮のデータを作成しました。

学生	数学	英語	物理	仕事
Aさん	0	1	1	1
Bさん	1	0	0	1
Cさん	0	1	0	0
Dさん	1	0	1	1

# numpyのインポート
import numpy as np

# ０：不合格、１：合格
# 合格状態のデータ
inputs = np.array([
    [0,1,1],
    [1,0,0],
    [0,1,0],
    [1,0,1]])

# ０：仕事見つからなかった、１：見つかった
# 仕事見つかった実績
outputs = np.array([
    [1],
    [1],
    [0],
    [1]])

パラメータの初期化

weight,biasなどのパラメータの初期化を行います。入力層のノードの数が３であるため、3 x 1 のweightsを作成します。biasは１つのみです。
学習データが少ないため、learning rateとエポック数を少なめに設定します。これらの値を変える事で結果が全然違うことになるケースが多いです。ですので、最適の値を見つけるのが重要です。

# weightの初期化
weights = np.array([
    [0.5],
    [0.5],
    [0.5]])

# biasの初期化
bias = np.array([[0.2]])

# learning rateの初期化
lr = 0.1

# epochの初期化
epoch = 5000

学習の処理の中で使う関数を定義します。

def sigmoid(x):
    return 1/(1+np.exp(-x))

学習処理

# 学習開始
# start training
for _ in range(epochs):
    # feed forward
    # 予測
    prediction = np.dot(inputs, weights) + bias

    # 活性化
    activated_val = activate(prediction)

    # backpropagation
    # 画像の△w（der_cost_w）の計算
    error = activated_val - outputs
    sigmoid_der_prediction = activated_val * (1 - activated_val)
    der_cost_w = np.dot(inputs.T,  sigmoid_der_prediction * error)
    
    # 画像の△bの計算
    der_cost_b = sigmoid_der_prediction * error
    
    # Gradient Descentを使ってweightの調整
    weights -= learning_rate * der_cost_w
    # Gradient Descentを使ってbiasの調整
    bias -=  learning_rate * np.sum(der_cost_b,axis=0,keepdims=True)

# training completed
print("Loss  : {:.8f}".format(error))
print("weight: ", weights.T[0])
print("bias  : ", np.asscalar(bias))

評価

どのように学習したか評価します。

# 結果を表示するための関数
def get_prediction(data):
    pred = predict(data)
    msg = "仕事が見つかる" if round(np.asscalar(pred)) else "仕事が見つからない"
    print(data, msg, np.asscalar(pred))

# 全科目合格の場合は、仕事見つかるか
get_prediction([1,1,1])

# 物理のみ不合格の場合は、仕事見つかるか
get_prediction([1,1,0])

# 全科目不合格の場合は、仕事見つかるか
get_prediction([0,0,0])

今回は、サンプルデータが少ない事とネットワークが単純すぎるから間違った答えがおおいかもしれませんが、基礎の理解という事でご許しください。

Google Colab

直接Colabから実行することもできますので一度試してみてください。ちなみに、Colabのコメントはすべて英語です。
without_hidden_layers.ipynb

最後に

今回はニューラルネットワークの基礎を理解する目的で短い行数のコードでネットワークを作りました。次回は隠れ層ありのネットワークを構築しましょう。