BoTorch 実践 3. ノイズの扱い

---

BoTorch 入門 1.
BoTorch 入門 2.
BoTorch 入門 3.

BoTorch 実践 3. ノイズの扱い
BoTorch 実践4. 制約付きベイズ最適化

---

BoTorchでは観測ノイズを3通りの方法で扱うことができます.

以下のような感じです。

• Homoskedasticではノイズはハイパーパラメータの最適化として推論されます。このノイズは入力に関わらずどこでも同一のノイズが加わっているものとしてモデリングされます。
• Fixedではノイズは陽に与えられます。つまり例えば出力のノイズが何らかの方法でわかっている場合、入力と出力と観測ノイズの情報を渡すことでモデリングの精度を高めることに繋がります。ノイズはどの地点でも同一である必要はなく、逆にどの地点でもほとんど0とすることでノイズが無いとモデルに伝えることができます。ただ未知の入力点に対するノイズはわからないため未知の入力点での事後分布にはノイズの情報は含まれません
• HeteroskedasticではFixedと同様にノイズの情報が陽に与えられますが、入力とノイズの関係性を新たなガウス過程でモデリングするため、未知の入力点に対してもノイズを含んだ結果を返すことが可能です。

早速やっていきましょう。
単純な正規分布に従う観測ノイズでは面白くないので少し複雑な観測ノイズを加えてみます。

元の関数は$y = sin(x) ( -2 < x < 2)$ですが,$x$が原点から離れるほどノイズを大きくしていきます。

import torch
train_X = torch.linspace(-2,2,20,dtype=torch.float64).unsqueeze(-1)
train_y = torch.sin(train_X)

train_yvar = train_X**2 

train_y_noise = (train_y + train_yvar * torch.randn_like(train_y)).to(train_X)


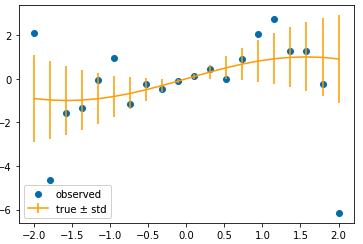
plt.scatter(train_X,train_y_noise,label="observed")
plt.errorbar(train_X,train_y,yerr=train_yvar.squeeze(-1).sqrt(),c="orange",label="true ± sigma")
plt.legend()

原点付近では値は元の関数とほとんど同じですが原点から離れるにつれ値が大きくなります。

これらをSingleTaskGP,FixedNoiseGP,HeteroskedasticSingleTaskGPでモデリングします。
学習させた後事後分布からサンプルを3つほどとってきます。

SingleTaskGP

from botorch.models import SingleTaskGP
from gpytorch.mlls import ExactMarginalLogLikelihood
from botorch import fit_gpytorch_mll
single_gp = SingleTaskGP(train_X,train_y_noise)
mll = ExactMarginalLogLikelihood(single_gp.likelihood,single_gp)
fit_gpytorch_mll(mll)

predict_X = torch.linspace(-2,2,100).unsqueeze(-1).to(train_X)
for _ in range(3):
   predict_y = single_gp.posterior(predict_X).rsample().detach()
   plt.plot(predict_X,predict_y.squeeze(0))

plt.title("SingleTaskGP")

ノイズの情報を与えていないので当然ですが、観測点に関してはよくフィッティングできていても元の関数とは大きく異なります。

FixedNoiseGP

from botorch.models import FixedNoiseGP
from gpytorch.mlls import ExactMarginalLogLikelihood
from botorch import fit_gpytorch_mll
fixed_gp = FixedNoiseGP(train_X,train_y_noise,train_yvar)
mll = ExactMarginalLogLikelihood(fixed_gp.likelihood,fixed_gp)
fit_gpytorch_mll(mll)

predict_X = torch.linspace(-2,2,100).unsqueeze(-1).to(train_X)
for _ in range(3):
   predict_y = fixed_gp.posterior(predict_X).rsample().detach()
   plt.plot(predict_X,predict_y.squeeze(0))

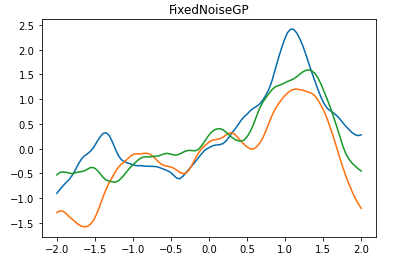
plt.title("FixedNoiseGP")

ノイズの情報を与えている分、特に原点付近は元の関数をよく近似できています。

HeteroskedasticSingleTaskGP

from botorch.models import HeteroskedasticSingleTaskGP
from gpytorch.mlls import ExactMarginalLogLikelihood
from botorch import fit_gpytorch_mll
hetero_gp = HeteroskedasticSingleTaskGP(train_X,train_y_noise,train_yvar)
mll = ExactMarginalLogLikelihood(hetero_gp.likelihood,hetero_gp)
fit_gpytorch_mll(mll)

predict_X = torch.linspace(-2,2,100).unsqueeze(-1).to(train_X)

plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
plt.title("")
for _ in range(3):
   predict_y = hetero_gp.posterior(predict_X,observation_noise=False).rsample().detach()
   plt.plot(predict_X,predict_y.squeeze(0))
plt.title("HeteroGP without noise")

plt.subplot(1,2,2)
for _ in range(3):
   predict_y = hetero_gp.posterior(predict_X,observation_noise=True).rsample().detach()
   plt.plot(predict_X,predict_y.squeeze(0))
plt.title("HeteroGP with noise")

HeteroskedasticSingleTaskGPではノイズを考慮するかそうでないかをobservation_noiseという引数で指定することができます。
ノイズなしではFixedNoiseGPと似たような結果ですが、ノイズありでは原点から遠いところでは分散の幅が大きくなっていることが確認できます。