機械学習の勉強を始めて、モーメンタム法やAdamが本当に効果があるのか気になったので、実際にPythonでグラフを描いて確かめてみました。
0. 最適化アルゴリズムとは
機械学習では、まず正解値を予測するために入力から適当な式を立てます。
例えば単回帰分析なら、
\hat{y} = ax+b
ここで$x$は入力、$\hat{y}$は予測値になります。
入力$x$と正解値$y$が与えられ、予測値$\hat{y}$が正解値$y$に近づくような$a, b$といったパラメータを求めるのが機械学習の流れになります。
$\hat{y}$と$y$がどれぐらい違うのか(損失)を表すのが損失関数です。損失関数の値が小さければうまく予測できていることになります。誤差関数も同じ意味です。
損失関数が小さくなるパラメータを見つけるのが、これから学ぶ最適化アルゴリズムです。
1. 勾配降下法
パラメータを損失関数の勾配を逆方向に進めていきます。以降の最適化アルゴリズムは全てこの勾配降下法をアレンジしたものになります。
w^{\left( t+1\right) }=w^{\left( t\right) }+\Delta w^{\left( t\right) }
\Delta w^{\left( t\right)}=- \eta \nabla E ( w^{\left( t\right) })
ここで $w^{\left( t\right) }$ は、時刻 $t$ (イテレーション)でのパラメータです。わかりにくいですが$w$はベクトルです。$\nabla E( w^{\left( t\right) })$は損失関数の勾配です。$\eta$ は学習率といって、どの程度勾配を下るのか制御します。
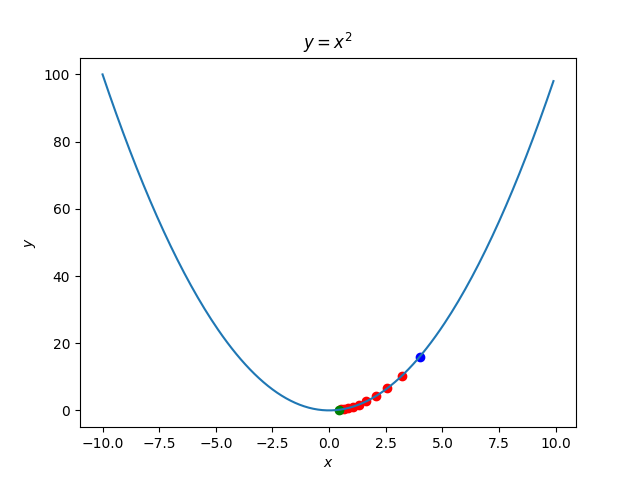
損失関数$E$が$y=x^2$の場合について考えてみましょう。$w$は$x$です。$\eta=0.1$とします。
初期値を$x^{\left( 0\right) }=4$に設定します。このとき$\Delta w^{\left( t\right) }=-0.8$なので、$x^{\left( 1\right) }=3.2$となり、きちんと勾配を下っていることがわかります。
損失関数が2変数でも同じです。
損失関数$E$が$z=\sin \left( \dfrac{x}{\pi }\right) \cdot \cos \left( \dfrac{y}{\pi }\right)$の場合では以下のようになります。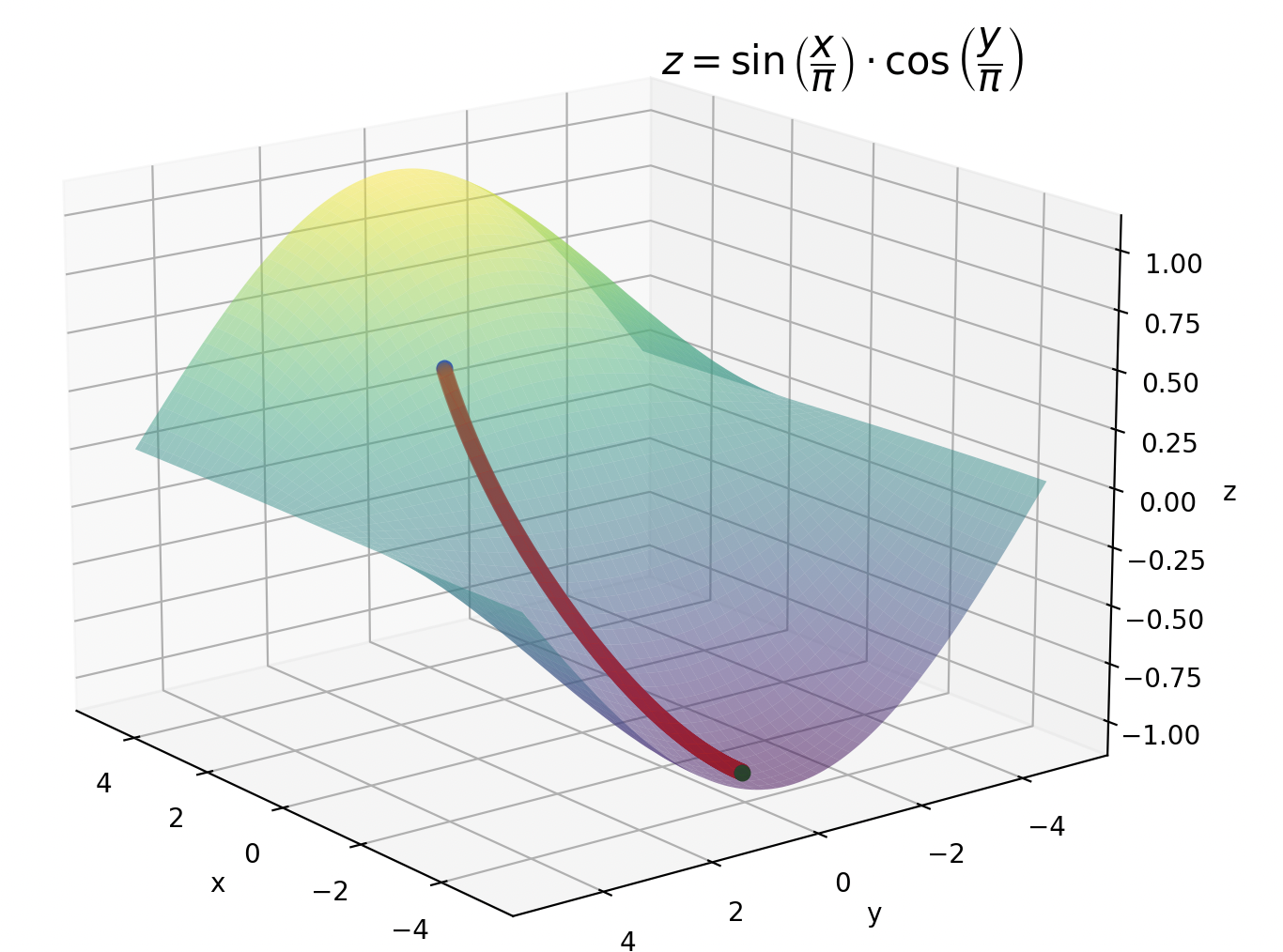
1.2 勾配降下法の欠点
勾配降下法では対応できないような損失関数を2つ紹介します。
1つ目は深い谷です。深い谷ではパラメータの更新が大きすぎるために、振動を起こしてしまいます。
$\eta$をもっと小さくすればパラメータの更新がもっと細かくなり振動は抑えられますが、谷ではない普通の勾配ではほとんど更新されなくなってしまいます。
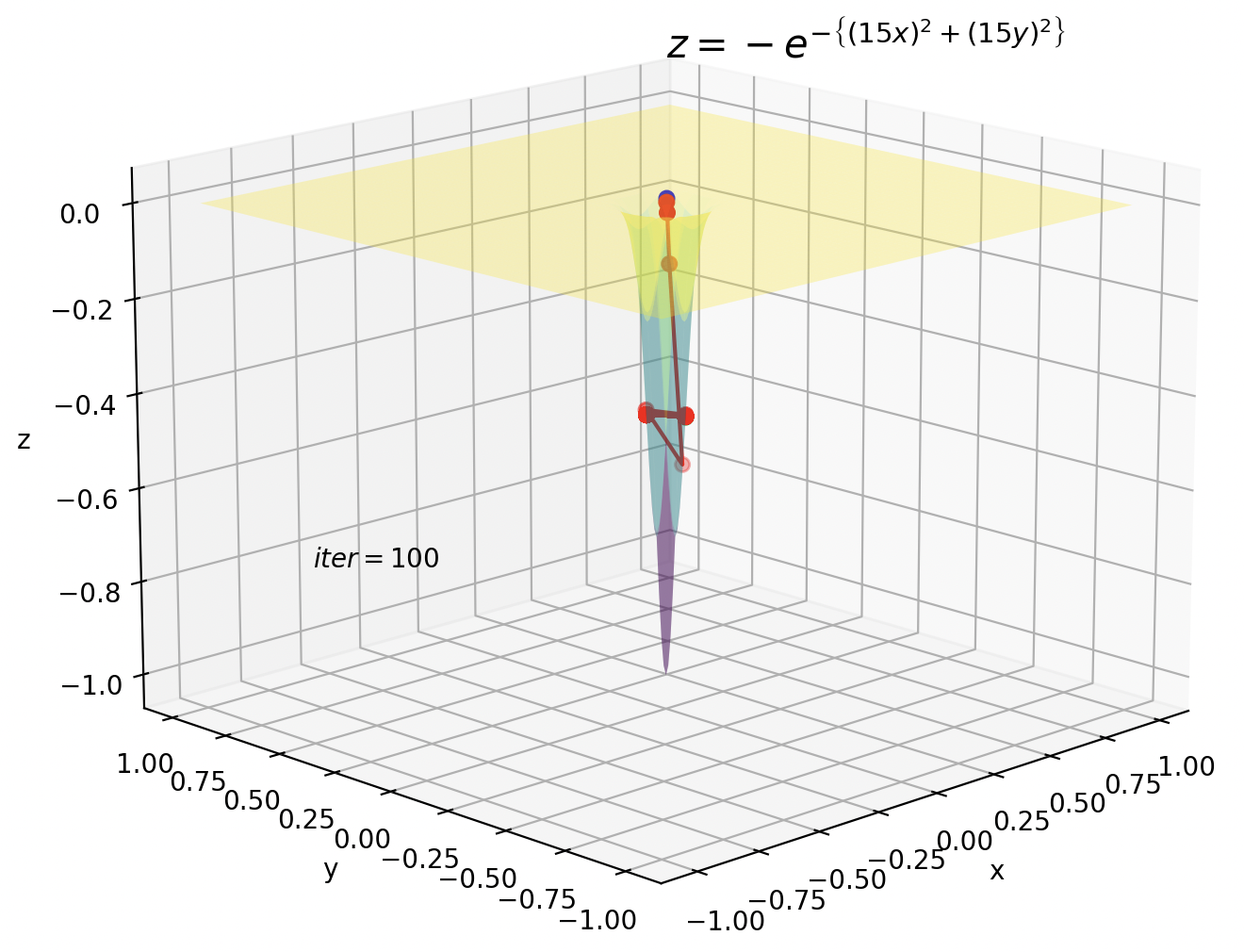
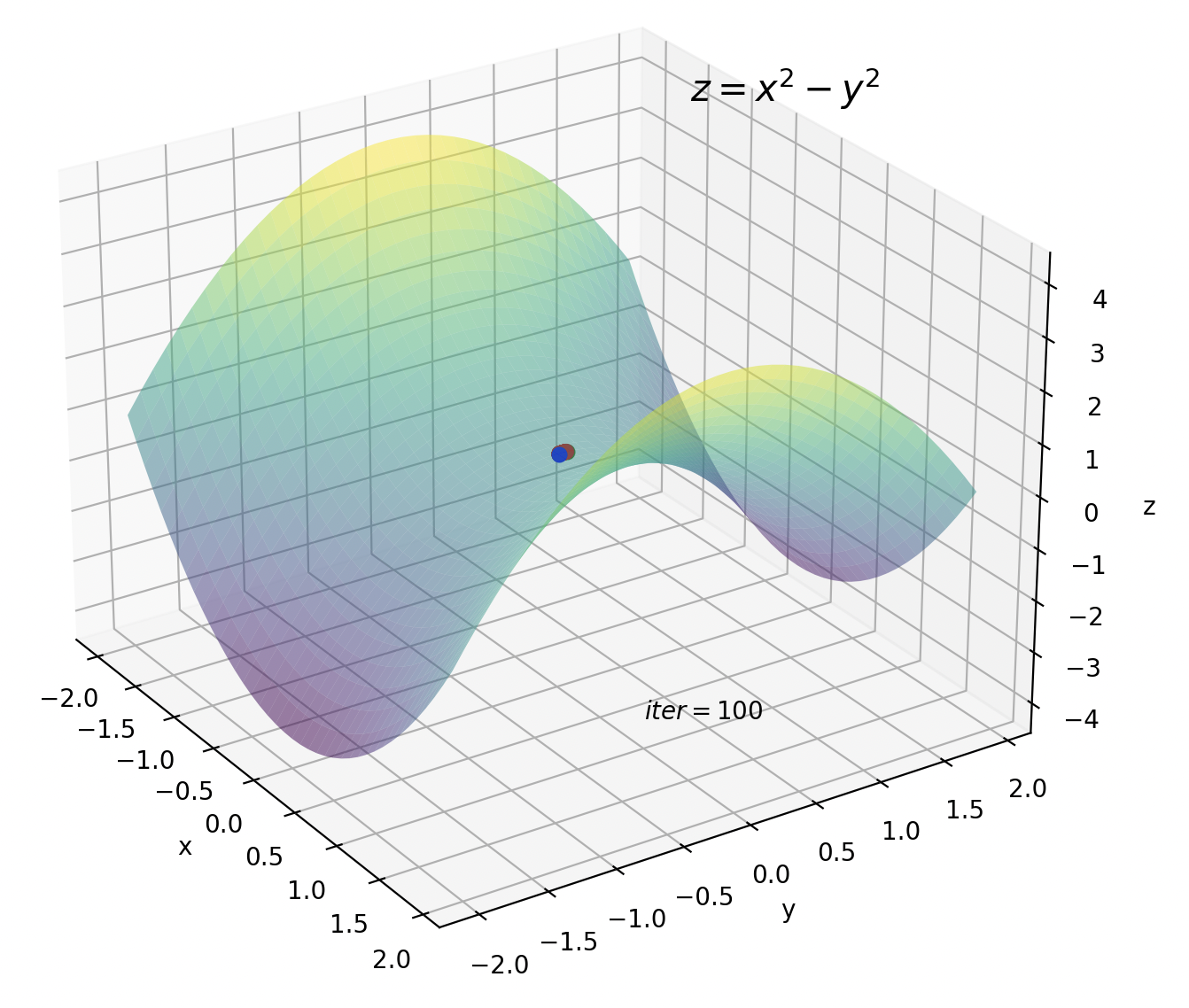
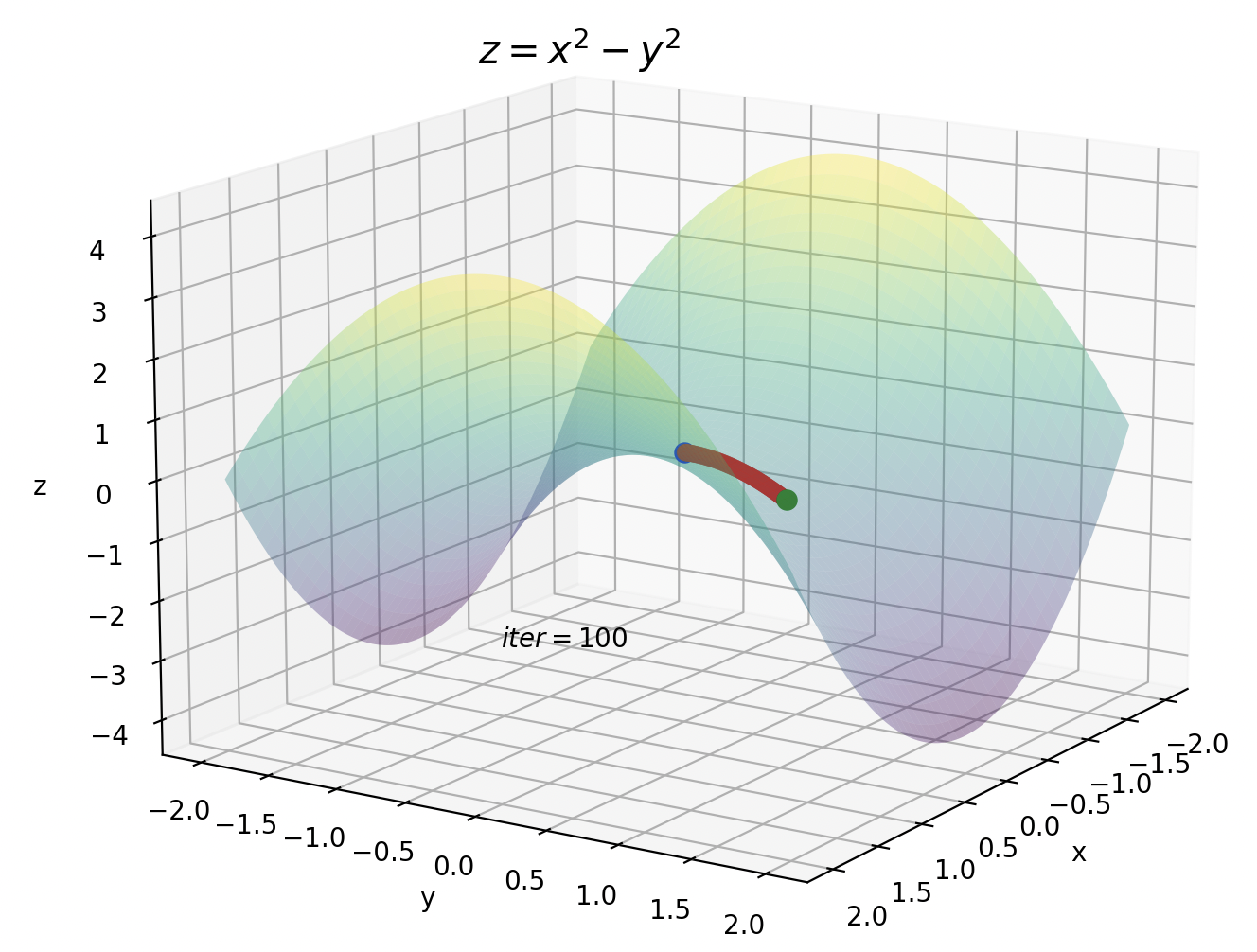
2つ目は鞍点です。鞍点の付近では勾配がほぼ0になるため、パラメータもほとんど更新されなくなります。
2. モーメンタム法
モーメンタム法は深い谷での振動を抑制することができます。モーメンタム(Momentum)は運動量という意味です。
w^{\left( t+1\right) }=w^{\left( t\right) }+\Delta w^{\left( t\right) }
\Delta w^{\left( t\right)}= \mu \Delta w^{\left( t-1\right)} -\left(1-\mu \right) \eta \nabla E( w^{\left( t\right) })
ポイントは前回の更新量$\Delta w^{\left( t-1\right)}$です。勾配降下法での更新量$-\eta\nabla E\left( w^{\left( t\right) }\right)$の一部を前回の更新量に置き換えるイメージです。その比率は$\mu$で調節します。
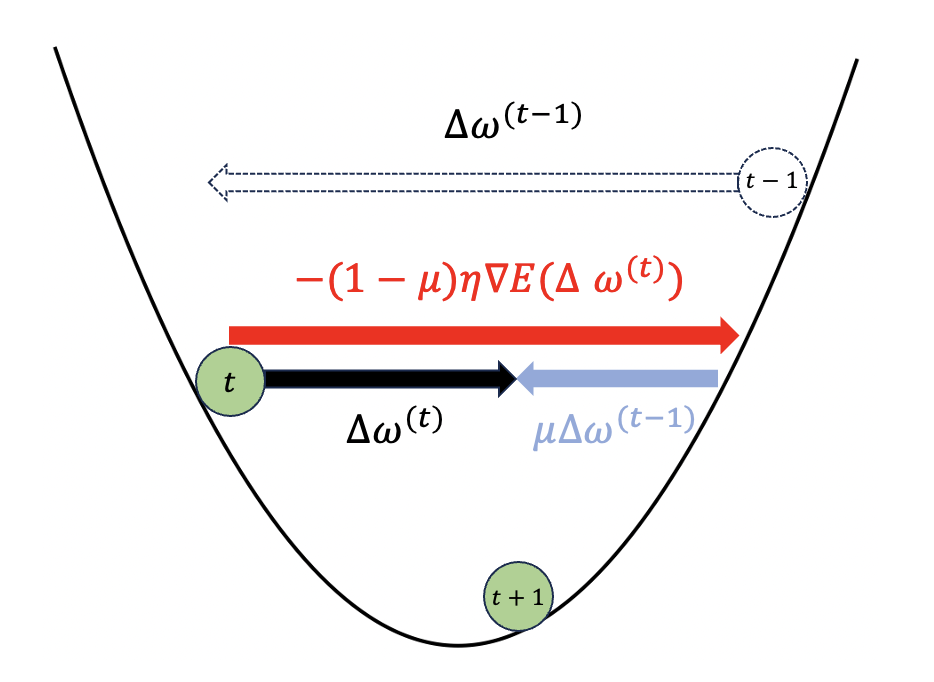
この図を見ると、前回のパラメータ更新量$\Delta w^{\left( t-1\right)}$は負で、今の勾配が負なので$-\left( 1-\mu \right)\eta\nabla E\left( w^{\left( t\right) }\right)$は正です。
よって今の更新量$\Delta w^{\left( t\right)}= \mu \Delta w^{\left( t-1\right)} -\left(1-\mu \right) \eta \nabla E( w^{\left( t\right) })$が勾配降下法のときよりも小さくなっています。
実際の効果を見てみましょう。
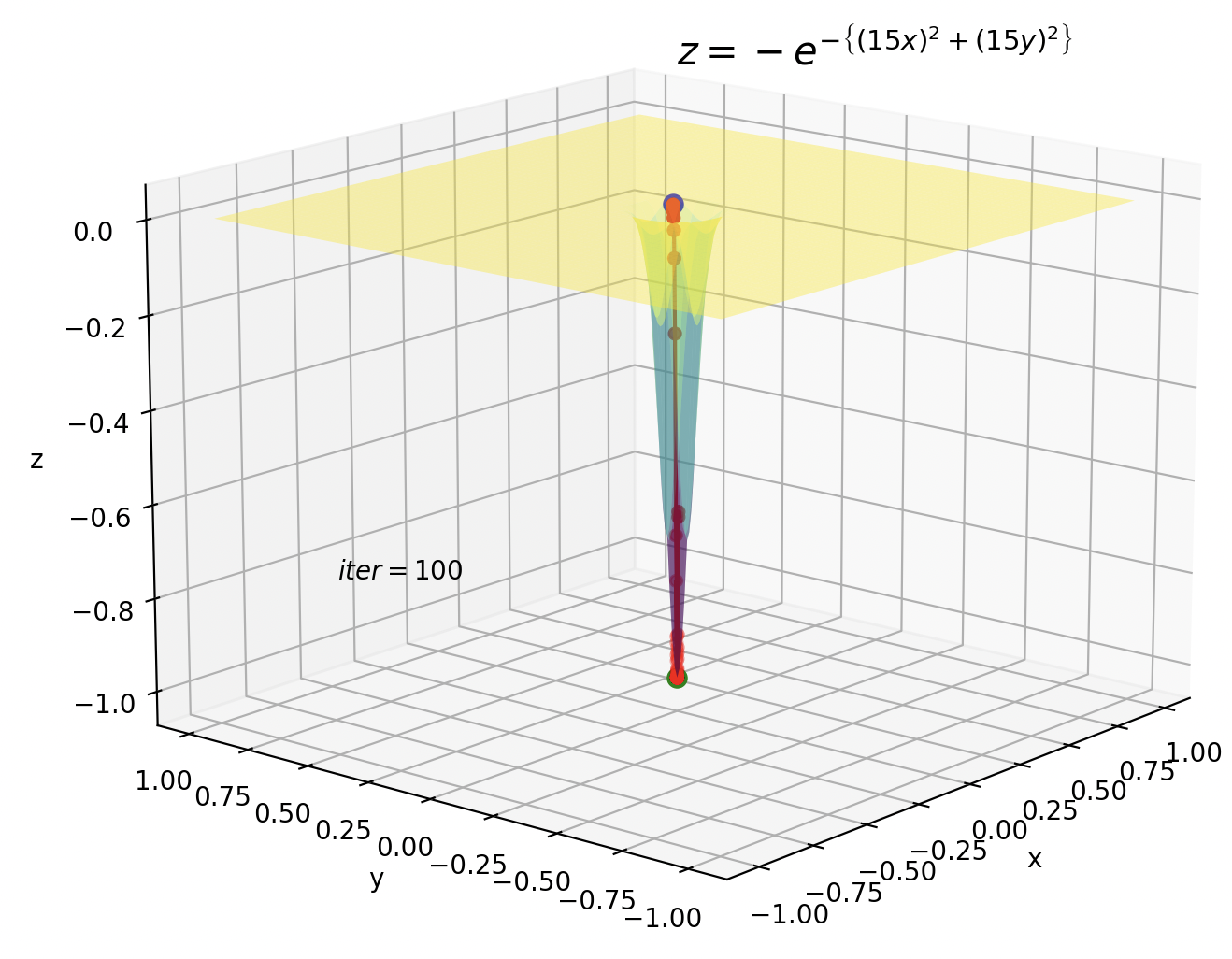
振動が抑えられて極小値に収束していることがわかります。
しかし、数式から分かるように、鞍点のように勾配がほぼ0のようなところでは効果がありません。
3. AdaGrad
勾配降下法では、全てのパラメータに対して学習率$\eta$が一つしかありませんでした。例えば、$x$方向には急激な勾配をもつ一方、$y$方向には緩やかな勾配しかもたない損失関数では、$x$方向にはどんどんパラメータが更新され、$y$方向には一向に更新が進みません。
AdaGradでは$\eta$を各パラメータ方向の勾配の総和で割ることで解決しています。
\Delta w_i^{\left( t\right)} = -\dfrac{\eta}{ \sqrt{\sum ^{t}_{s=1}\left( \nabla E ( \omega _i^{\left( s\right) } \right)^{2} }}\nabla E( w_i^{\left( t\right) })
$w$はベクトルなので、$w_0=x, \hspace{3mm} w_1=y$っていう感じです。
各パラメータの勾配の総和で割ることで、以前まで勾配が急だった方向には学習率を小さく、勾配が緩やかだった方向には学習率を大きくすることが可能になります。
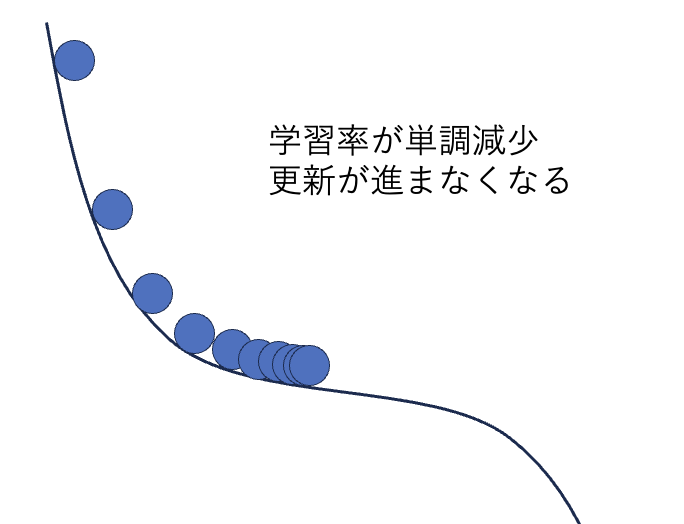
AdaGradの欠点
しかしAdaGradには致命的な欠点があります。それは学習率が単調に減少するということです。つまり、急な勾配の後に緩やかな勾配がくる場合、学習率が小さくなっているため緩やかな勾配では更新量はほぼ0になってしまいます。
4. RMSprop
AdaGradの問題はひとたび更新量が小さくなってしまうと、大きな値には戻らないことでした。そこで、十分過去の勾配については指数的な減衰因子をかけることで消滅させましょう。
v_{i, t}=\rho v_{i, t-1}+(1-\rho) \left( \nabla E( w^{\left( t\right) })_{i}\right)^{2}
\Delta w^{(t)}_i = -\dfrac{\eta}{\sqrt{v_{i, t}+ \varepsilon }}\nabla E( w^{\left( t\right) })_i
初期値は$v_{i, 0}=0$とします。$\varepsilon$は分母が0とならないように導入していて、$\varepsilon = 10^{-6}$などが用いられます。
例えば$t=100$のとき、$v_{i, 100}=\rho ^{99}(1-\rho)\left( \nabla E( w^{\left( 1\right) })_{i}\right)^{2}+\ldots$のように、$t=1$のときの勾配の情報がほぼ0になっています。
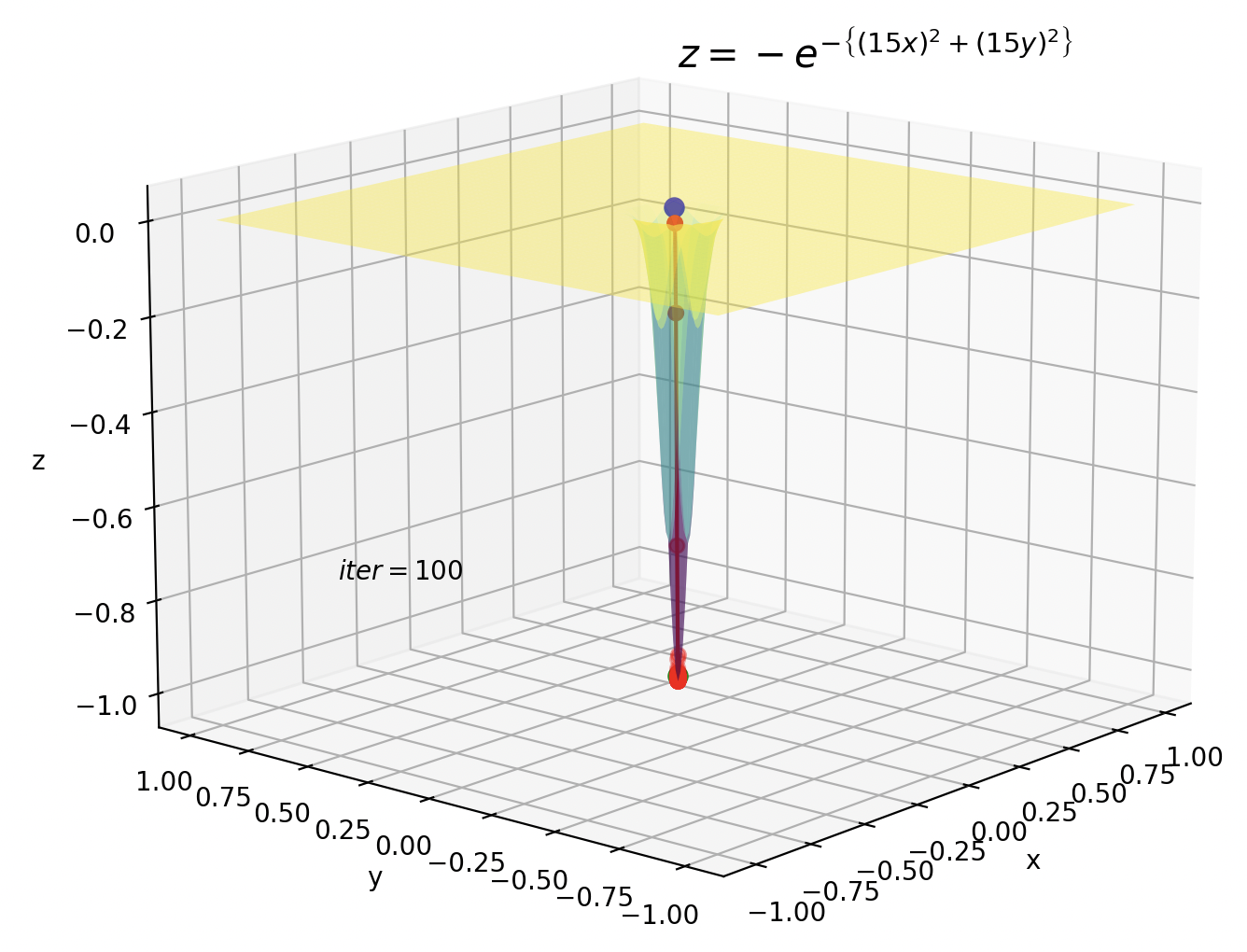
5. Adam
AdamはRMSpropとモーメンタム法を融合させたものになります。
m_{i, t}=\rho_1 m_{i, t-1} + (1-\rho_1)\nabla E(w^{(t)})_i
v_{i, t}=\rho_2 v_{i, t-1} + (1-\rho_2)\left( \nabla E(w^{(t)})_i \right)^2
ここでもう一手間加えます。$m$と$v$は初期値を0にとっているので、更新の初期はモーメントが0の方に偏ってしまいます。これを解消するために、新しく$\widehat{m}$と$\widehat{v}$を導入します。
\hat{m}_{i, t}=\dfrac{m_{i, t}}{(1-(\rho_1)^t)}
\hat{v}_{i, t}=\dfrac{v_{i, t}}{(1-(\rho_2)^t)}
更新の初期には分母が小さくなりモーメントが増幅されます。
\Delta w^{(t)}_i = -\eta \dfrac{\hat{m}
_{i, t}}{\sqrt{\hat{v}_{i, t}+ \varepsilon }}
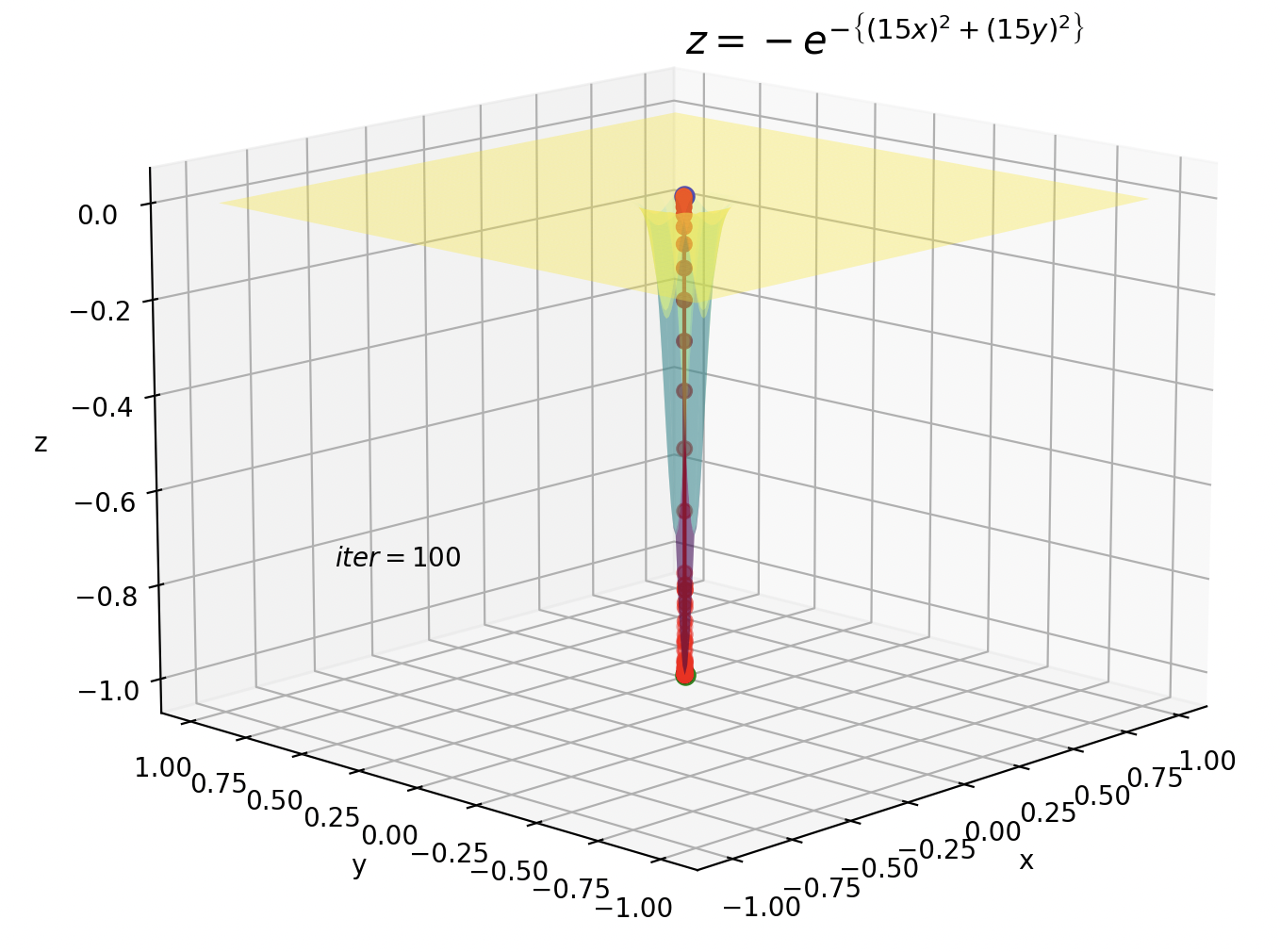
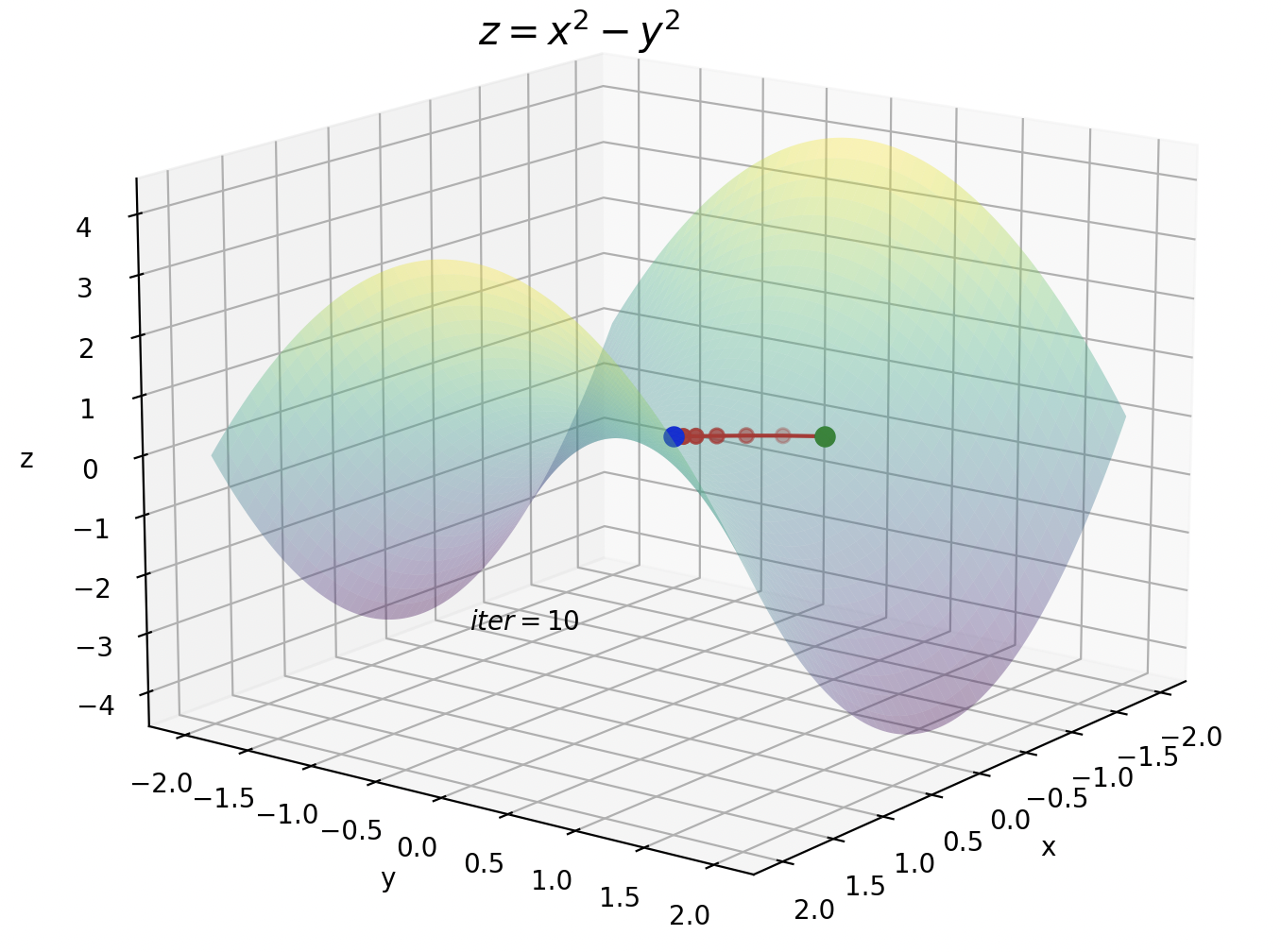
鞍点の方はイテレーションが10です。今までのイテレーションが100だったことを考えると、Adamがいかに早く暗転を抜けているかが実感できます。
おわりに
勾配降下法からAdamまでをグラフを中心に解説しました。式だけでなくグラフで確認することでよりイメージしやすくなったと思います。
ニューラルネットワークの学習における停滞はほとんどが鞍点によるものだと言われています。ただし、損失関数によってはAdamよりもAdaGradの方が精度がいいという場合もあるので、状況に応じて適切な最適化アルゴリズムを選択することが求められます。
機械学習を勉強し始めてまだ日が浅いので、間違っているところがあれば教えてくれると非常にありがたいです。
参考
・これならわかる深層学習入門 (書籍)
・【決定版】スーパーわかりやすい最適化アルゴリズム -損失関数からAdamとニュートン法- (Qiita)
・ニューラルネットワークによる学習の停滞はどこから生ずるか
・確率的勾配降下法の大雑把な意味