はじめに
CAEで片持ち梁の応力解析をするさい、一方の端面を固定端とするために完全固定すると、固定端が特異点となってしまい、材料力学の理論で得られる最大応力値との比較が難しくなります。ここでは、片持ち梁の応力解析で得られる最大応力値を材料力学の理論値と比較するため、水野さまの書籍$^{(1)}$に載っていた梁の固定端における境界条件の設定方法を参考にして、梁の曲げの解析を行いました。
使用したモデル
FreeCADを使って、幅20mm、厚さ10mm、長さ400mmのモデルを作成しました。このモデルの片側の端面は
のように4分割してあります。この端面は固定端になります。面の分割はXSimさまの記事$^{(2)}$を参考にして行っています。なお、モデルの長手方向をx、幅方向をy、厚さ方向をzにとっています。
作成したモデルはstepファイル形式でエクスポートしておきます。作成したモデルは以下に格納してあります。
このモデルのstepファイルをPrePoMaxで読み込みます。
メッシュ、材料、Sections、Stepsを設定します。
- メッシュ：Meshing Parameters で Max element size を 2mm に
- 材料：Material Library で S235 を選択
- Sections：モデル全体を選択
- Steps：Static Step を選択
荷重は自由端（固定端の反対側）の角の各節点に5.9524 N（1節点あたり）×21節点≒125.0 N を加えています（下図）。
この梁において、材料力学で求まる固定端の最大応力$\rm{\sigma_{max}}$と自由端の最大たわみ$w$は次のようになります。これらの値には、梁の自重による応力とたわみは含まれません。
- $\rm{\sigma_{max}}$ : 150.0 MPa
- $w$ : 7.619 mm
※これらの値は以下のサイトで計算
固定端の面の固定方法は次の4種類について行いました。
- 面全体を完全固定
- 面全体のx方向の変位を0、中立線z=0におけるy方向とz方向の変位を0
- 面全体のx方向の変位を0、中立線y=0におけるy方向とz方向の変位を0
- 面全体のx方向の変位を0、中立線z=0におけるz方向の変位を0、中立線y=0におけるy方向の変位を0
1の方法の固定端の面の固定のようす
2の方法の固定端の面の固定のようす
3の方法の固定端の面の固定のようす
4の方法の固定端の面の固定のようす
これらの方法による解析結果を下表に示します。
| 方法 | $\rm{\sigma_{max}}$ (MPa) | $w$ (mm) |
|---|---|---|
| 1 | 210.2 | 7.60 |
| 2 | 157.6 | 7.62 |
| 3 | 172.3 | 7.62 |
| 4 | 157.6 | 7.62 |
この表において、最大変位はいずれの方法も理論値とほぼ一致しています。これに対して固定端の最大応力は、方法1では理論値の4割増しとなっていますが、固定方法を工夫した方法2～4では方法1に比べて理論値に近い値が得られ、特に方法2と4では理論値に近い値となっています。
材料力学の梁の曲げ理論は、梁の長手方向だけに応力が生じる、いわゆる単軸応力状態を仮定していますが、CAEで解析するときは梁の固定端の面を長手方向以外の方向に拘束する必要があるため単軸応力状態とはならず、y方向やz方向にも応力が生じます。
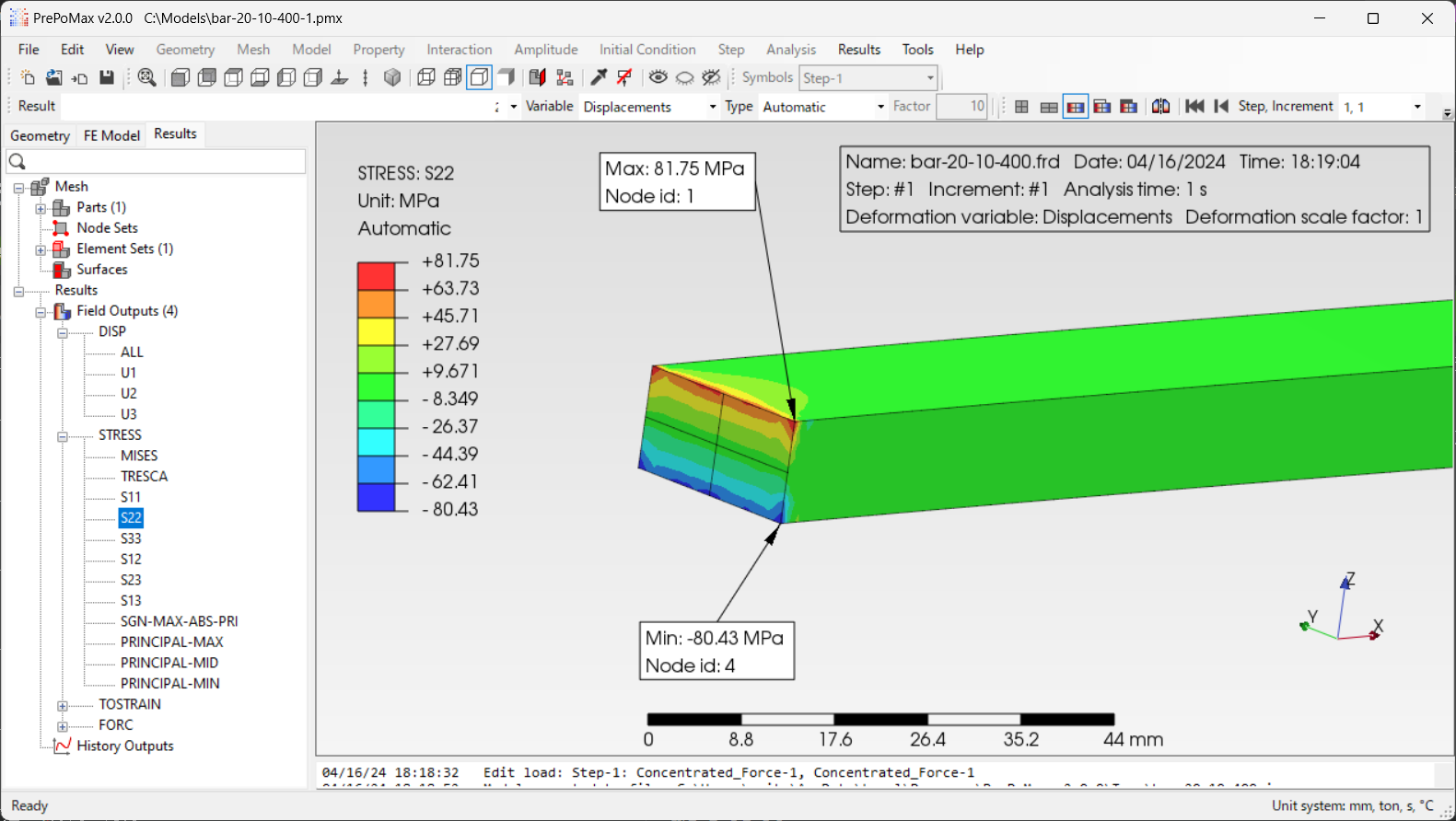
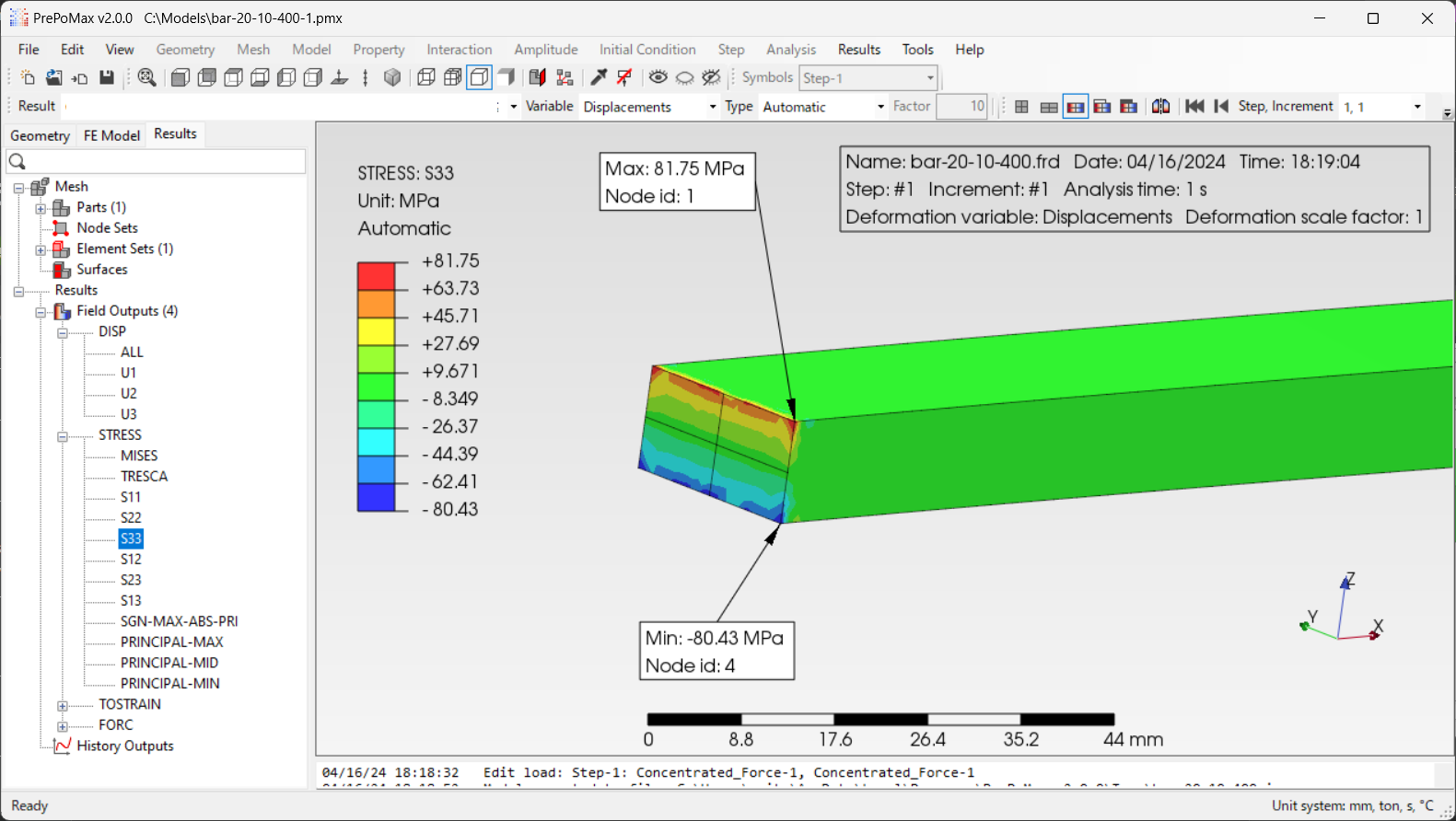
ただ、今回ご紹介したように境界条件を工夫することで、y方向やz方向に生じる応力の範囲を小さくすることはできます。下図に方法1と方法4について、固定端付近のy方向とz方向の応力分布を示します。応力値が理論値に近い値となる方法4は、方法1に比べて高い応力を示す範囲が狭くなっていることが分かります。
方法1による固定端付近のy方向の応力
方法1による固定端付近のz方向の応力
方法4による固定端付近のy方向の応力
方法4による固定端付近のy方向の応力
終わりに
境界条件を工夫することにより、片持ち梁の特異点となる場所においても理論値に近い応力値が得られることを紹介しました。参考文献(1)には、このようなCAEを使いこなす上で必要な考え方や方法が載っています。興味ある方は一読されることをお勧めします。
参考文献
(1) 水野操, 材料力学を理解してCAEを使いこなす CAEのよくある悩みと解決法, 2024年, 145-166ページ, 日刊工業新聞社
(2) FreeCAD平面を複数の面に分割する