はじめに
PrePoMaxを使って円孔をもつ長方形板の応力計算を行いました。モデルはFreeCADで作成しています。
FreeCADによるモデルの作成
図1に示す円孔をもつ長方形板の1/4モデルをFreeCADでスケッチします。

図1 円孔をもつ長方形板とその1/4モデル(破線部)
作成したスケッチから、厚さ1mmにPadしたモデルと、スケッチのエッジをFaceに変換したモデルを作成して、それぞれSTEPファイルにエクスポートします。
FreeCADで作成したモデルはこちらにあります。Pad.stepとface.stepというファイルです。
PrePoMaxによるSolidモデルの応力計算
PrePoMaxにPadのモデルをインポートします。
メッシュを作成します。メッシュの最大サイズは2mmとします。
境界条件は、対称面に垂直な変位を0とし、板の端面にSurfaceTractionとして4000Nを加えます。材料は鋼(ヤング率210000MPa、ポアソン比0.3)です。このモデルは幅が1/2ですので、実際には8000Nの力を加えたことに相当します。
メッシュと境界条件を設定したようすを図2に示します。

図2 ソリッドモデルのメッシュと境界条件
応力の計算結果を図3に示します。板の長手方向の垂直応力は穴の縁で最大値884MPaで、穴から遠い位置(X=11.78mm、Y=84.21mm)では4000Nを断面積(幅20mm×厚さ1mm)で割った値200MPaとなっていることが分かります。

図3 ソリッドモデルの長手方向の垂直応力の計算結果
PrePoMaxによるShellモデルの応力計算
PrePoMaxにFaceのモデルをインポートします。
メッシュと境界条件をSolidモデルと同様に設定します。ただし、対称面の境界条件については、対称面に垂直な変位を0とすることに加えて、対称面が回転しない条件が必要になります。ハーフモデル(対称条件)の設定方法|CAEトピックスなどに説明が載っています。ここでは、表1のように設定します。
表1 Shellモデルの対称面における境界条件
| パラメータ | 長さ方向断面 | 幅方向断面 |
|---|---|---|
| U1 | 0 mm | Unconstrained |
| U2 | Unconstrained | 0 mm |
| U3 | Unconstrained | Unconstrained |
| UR1 | Unconstrained | 0 rad |
| UR2 | 0 rad | Unconstrained |
| UR3 | 0 rad | 0 rad |
メッシュと境界条件を設定したようすを図4に示します。
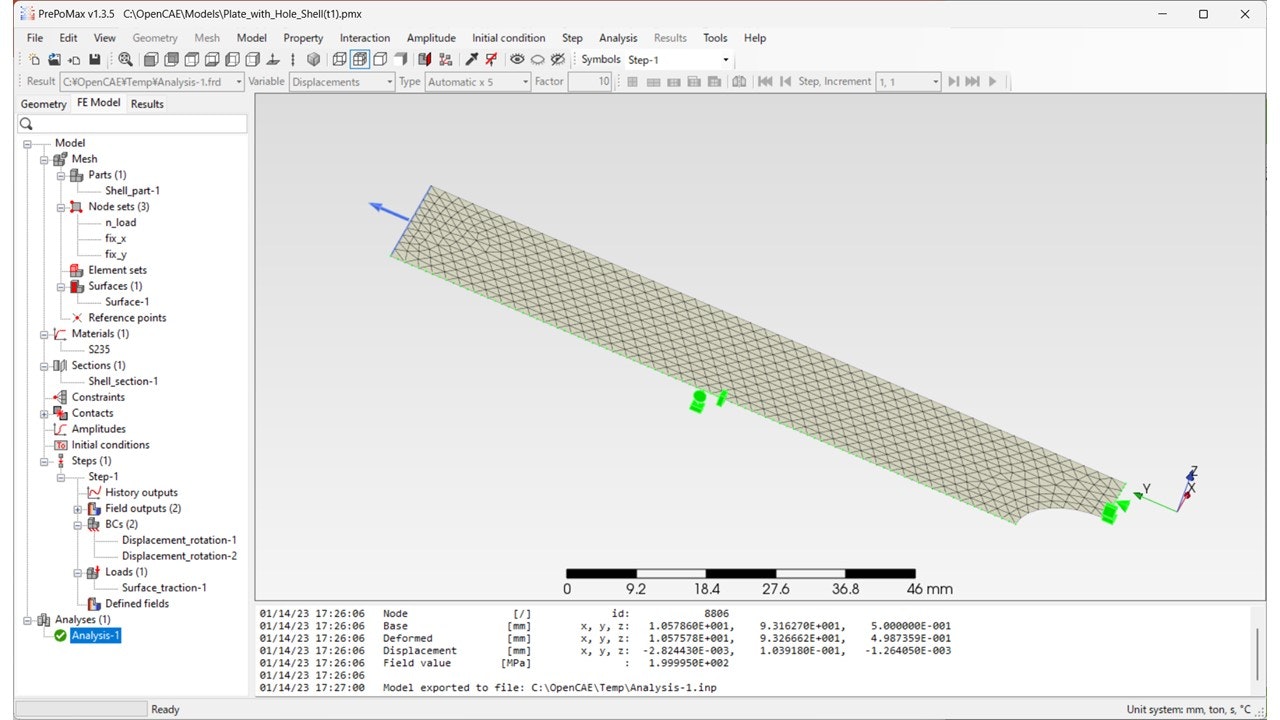
図4 シェルモデルのメッシュと境界条件
応力の計算結果を図5に示します。板の長手方向の垂直応力は穴の縁で最大値843MPaとなり、穴から遠い位置(X=10.58mm、Y=93.27mm)では200MPaとなっていることが分かります。Solidモデルと同様な結果が得られました。

図5 シェルモデルの長手方向の垂直応力の計算結果
最後に、シェルモデルにおいて、表1のUR1~UR3をすべてUnconstrainedとして計算した結果を図6に示します。比較のため、表1の回転拘束した結果を図7に示します(図7は図5の見る方向を変えたものです)。対称面に回転拘束をしない場合、対称面で板が曲がってしまうことが図6から分かります。

図6 シェルモデルにおいて、対称面の回転拘束をしなかった場合の計算結果

図7 シェルモデルにおいて、対称面を回転拘束した場合の計算結果(図5の見る方向を変えたもの)