次元削減手法として,主成分分析やラプラシアン固有マップ法,Isomap,Locally Linear Embedding,t-SNE等が提案されている[1].これらの手法は,書籍や記事等でよく見られるが,実際に適切に次元圧縮されているかどうか評価する手法に関する記載が見当たらない.そのため,本記事では,次元圧縮の適切性を評価する手法として提案されているCo-Ranking Matrixを用いた手法[2]について簡単に解説する.
Co-Rankingのフレームワーク
Ranking という言葉から想像される通り,各標本点に関して自分以外の標本点との近さをランク付けした時,次元圧縮前と次元圧縮後でどれぐらい近い関係が保証されているかを評価するものである.高次元空間における標本点$\xi_i,\xi_j$間の距離を$\delta_{ij}$,低次元空間における標本点$x_i,x_j$間の距離を$d_{ij}$とする(データ数は$N$である).高次元空間における$\xi_i$に関する$\xi_j$の近さランクとして,
$$\rho_{ij}=|\{k|\delta_{ik}<\delta_{ij}\lor(\delta_{ik}=\delta_{ij}\land 1\le k<j\le N)\}|$$
とする(集合$A$に関して$|A|$は要素数を表す).同様に,低次元空間における$x_i$に関する$x_j$の近さランクとして,
$$r_{ij}=|\{k|d_{ik}<d_{ij}\lor(d_{ik}=d_{ij}\land 1\le k<j\le N)\}|$$
とする.この時,Co-Ranking 行列$Q$を次のように定義する.
$$Q_{kl}=|\{(i,j)|\rho_{ij}=k\land r_{ij}=l\}|$$
すなわち,$Q$の対角要素はランクが変わっていない分を表し,非対角要素はランクエラーを表している.この非対角要素をどこまで許容するかが,評価の鍵となる.
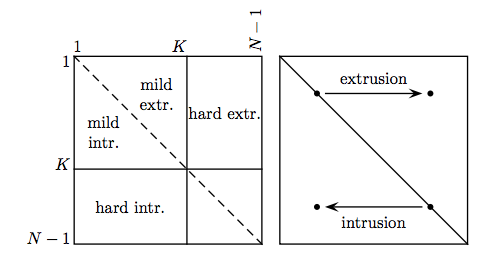
低次元でランキングが大きく,高次元でランキングが小さいようなエラーを extrusion, 低次元でランキングが小さく,高次元でランキングが大きいようなエラーを intrusion という.また,ランキングが高い(1位に近い)関係の方が保存されていることが望ましい.逆に,ランキングが低い関係はあまり保存されていなくても良い(例えば,近さ180位が近さ200位になったところでどうでも良い).ランキング高いエリアを mild,ランキングが低いエラーを hard という.これらをまとめると,次の図となる.
$K$近傍までの点が保存されていることが望ましいと考えると,評価指標$Q_{NX}(K)$は次のように定式化できる.
$$Q_{NX}(K)=\frac{1}{KN}\sum_{k=1}^K\sum_{l=1}^K Q_{kl}$$
これは,mild extr, mild intr, hard extr, hard intr のうち,mild extr, mild intr に入っている比率を表しているイメージとなる.言い換えると,高次元空間あるいは低次元空間において$K$近傍までのデータのうち,もう一方の空間において$K$近傍以内に入っているデータの比率となっている.そのため,この指標が高いほど,適切な次元削減が行われていると考えられる.
ランクエラーに基づく質基準に基づいた評価
しかし,前述のような評価指標では,1近傍にあったデータが圧縮後$K$近傍(ある標本からの近さのランクがK番目であること)になるエラーはカウントされないが,$K$近傍だったデータが圧縮後$K+1$近傍になるエラーはカウントされてしまう.これでは適切な評価ができないことが予期されるであろう.なぜこれでうまくいかなかったかと言えば,カットオフランキング(どこ以上のランキングを無視するか)も許容数(第何近傍まで許容するか)も同じ$K$で与えてしまっていて,柔軟性が欠けていたからである.そのため,パラメータ$K$を分割して考える.
前述の方法では,カットオフ指標$w_s$,許容指標$w_t$を次のように与えて$Q_{NX}(K)$を計算していたと考えられる.
w_s(\rho_{ij},r_{ij},K)=\left\{\begin{array}{cl}0&\rho_{ij}>K\land r_{ij}>K\\1&else\end{array}\right.\\
w_t(\rho_{ij},r_{ij},K)=\left\{\begin{array}{cl}0&(\rho_{ij}\le K\land r_{ij}>K)\lor(\rho_{ij}>K\land r_{ij}\le K)\\1&else\end{array}\right.\\
Q_{NX}(K)=\frac{1}{KN}\sum_{i=1}^N\sum_{j=1}^Nw_s(\rho_{ij},r_{ij},K)\cdot w_t(\rho_{ij},r_{ij},K)
ここで,$K$の役割を分担し,$w_s$に関するものを$\kappa_s$,$w_t$に関するものを$\kappa_t$とする.また,許容指標はランクエラーの距離として定義し直す.
w_t(\rho_{ij},r_{ij},\kappa_t)=\left\{\begin{array}{cl}0&|\rho_{ij}-r_{ij}|>\kappa_t\\1&else\end{array}\right.
すなわち,高次元空間と低次元空間においてランク差が$\kappa_t$以下なら許容するものになる.これは,前述のような1近傍が$K$近傍,$K$近傍が$K+1$近傍になる例に関する問題を生じさせない.新たな$Q'_{NX}(\kappa_s,\kappa_t)$は次のように定義される.
Q'_{NX}(\kappa_s,\kappa_t)=\frac{1}{\kappa_sN}\sum_{i=1}^N\sum_{j=1}^Nw_s(\rho_{ij},r_{ij},\kappa_s)\cdot w_t(\rho_{ij},r_{ij},\kappa_t)
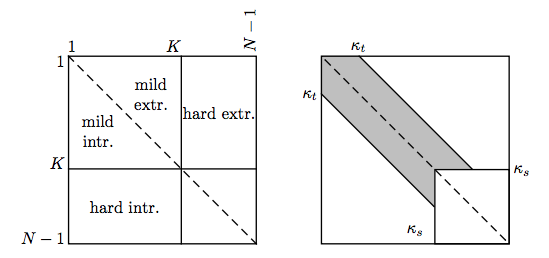
イメージ図としては次のようになる.
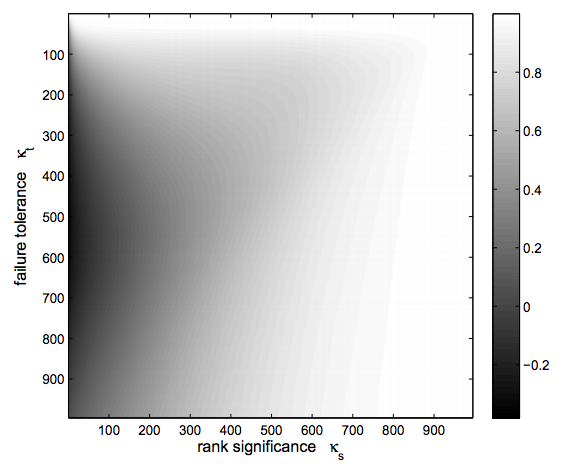
また,評価するにあたっては複数の$\kappa_t,\kappa_s$に関して実行しヒートマップを描くと良い.
標本点ごとの評価
各標本点に関してランキングが保存されているかを測るのもボトルネックを探る上では有益である.$i$番目の標本に関して,評価は次のようにするのが自然と思われる.
$$Q_i'(\kappa_s,\kappa_t)=\frac{1}{\kappa_sN}\sum_{j=1}^Nw_s(\rho_{ij},r_{ij},\kappa_s)\cdot w_t(\rho_{ij},r_{ij},\kappa_t)$$
しかし,これでは行列$Q$の列要素しか考えていないことになる.すなわち,高次元空間における近さが低次元空間で保存されているかしか見ていない.もちろんそれで良いこともあるが,低次元空間における近さが高次元空間でも同様であるかも見たい.すなわち,対称性を確保するために次のように定義を改める.
$$Q_i'(\kappa_s,\kappa_t)=\frac{1}{2\kappa_sN}\sum_{j=1}^N(w_s(\rho_{ij},r_{ij},\kappa_s)\cdot w_t(\rho_{ij},r_{ij},\kappa_t)+w_s(\rho_{ji},r_{ji},\kappa_s)\cdot w_t(\rho_{ji},r_{ji},\kappa_t))$$
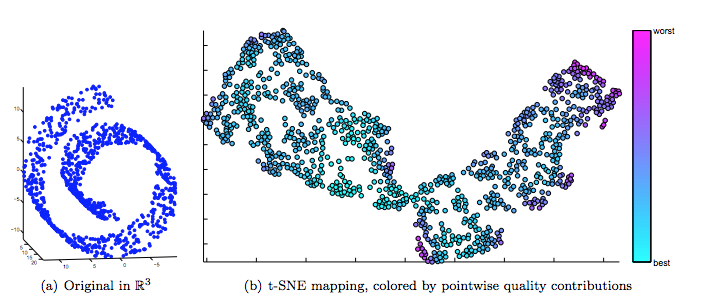
実際に,有名な swiss roll に対して,t-SNE を適用した結果を標本毎に評価したのが次の図である.
実装
次のクラスを作れば良い(実際に実装した).
def _parallel_calculate_rank(vector):
return rankdata(vector, method='ordinal')
class CoRanking(object):
def __init__(self, original_data, metric='euclidean', num_cpu=multi.cpu_count()):
self.original_data = original_data
self.metric = metric
self.num_cpu = num_cpu
self.original_rank = self._calculate_rank_matrix(original_data)
def _calculate_rank_matrix(self, data):
# calculate distance matrix
distance_matrix = metrics.pairwise.pairwise_distances(data, data, metric=self.metric)
# calculate rank matrix
p = Pool(self.num_cpu)
rank_matrix = p.map(_parallel_calculate_rank, distance_matrix)
p.close
return np.array(rank_matrix)
def evaluate_corank_matrix(self, dr_data, significance=96, tolerance=70):
# calculate rank matrix for dimensionality reduction data
self.dr_rank = self._calculate_rank_matrix(dr_data)
# reduct to only tolerance data
difference_rank = np.absolute(self.original_rank - self.dr_rank)
remain_tolerance = difference_rank < tolerance
# reduct to only siginifcance data
remain_significance = np.array([self.original_rank < significance, self.original_rank < significance]).any(axis=0)
# reduct both
return np.sum(np.array([remain_tolerance, remain_significance]).all(axis=0)) / (significance * len(dr_data))
def multi_evaluate_corank_matrix(self, dr_data, significance_range = range(10, 96),
tolerance_range = range(10, 70)):
# calculate rank matrix for dimensionality reduction data
self.dr_rank = self._calculate_rank_matrix(dr_data)
# calculate difference between rank matrices
difference_rank = np.absolute(self.original_rank - self.dr_rank)
# result
result = np.zeros((len(significance_range), len(tolerance_range)))
for i, significance in enumerate(significance_range):
for j, tolerance in enumerate(tolerance_range):
# reduct to only tolerance data
remain_tolerance = difference_rank < tolerance
# reduct to only siginifcance data
remain_significance = np.array([self.original_rank < significance, self.original_rank < significance]).any(axis=0)
# reduct both
result[i, j] = np.sum(np.array([remain_tolerance, remain_significance]).all(axis=0)) / (significance * len(dr_data))
return result
単一の値を得たければ,
cr = CoRanking(data)
cr.evaluate_corank_matrix(data_dr, kappa_s, kappa_t)
とすればよく,ヒートマップとして複数の値で計算したければ,
cr.multi_evaluate_corank_matrix(data_dr, range(2, 96), range(2, 88))
のようにすれば良い.ただし,'data' は高次元空間におけるデータを意味し,'data_dr' は次元削減後の低次元空間におけるデータを意味する.
最後に
- 実装は大変簡単でした.捻りがないので.
- 指摘や他の手法の紹介等よろしくお願いします.
参考文献
- Kerstin Bunte, Michael Biehl, Barbara Hammer. Dimensionality reduction mappings. http://www.cs.rug.nl/~biehl/Preprints/2011-IEEE-Paris-Kerstin.pdf, 2011.
- Wouter Lueks , Bassam Mokbel , Michael Biehl, Barbara Hammer. How to Evaluate Dimensionality Reduction? – Improving the Co-ranking Matrix. https://arxiv.org/pdf/1110.3917.pdf, 2011.