1. データの分割
機械学習では、訓練データとテストデータの2つに分けて、訓練データで学習させたモデルを作って精度を測ります。もしも、手持ちのデータを全て学習用データとして使用した場合、学習用データに過度に適合したモデルが出来上がってしまい、精度が悪くなってしまう「過学習」と呼ばれる状態になってしまう場合があります。
過学習を防ぐためにはデータを分割して、学習用データとテストデータを作って精度を測りながら最適な重み付けをモデルにしていきます。
今回はそのデータを分割する2つの方法「Hold-out」と「K-Fold」について紹介します。
そして、「Hold-out」と「K-Fold」を用いて機械学習を行い、両者でどれくらい精度に違いが出るかを確かめて行きたいと思います。
2. Hold-out
Hold-out(ホールドアウト法)は全データを学習用データとテストデータに分割してモデルの精度を確かめる方法です。分割の割合は、一般的に学習用データ8割、テストデータ2割とすることが多いです。

Hold-outのメリットとデメリットは下記になります。
メリット
・簡単に実装することが出来る。
・実行時間が短い
デメリット
・分割した学習用データとテストデータに偏りがあると過学習が起きてしまう
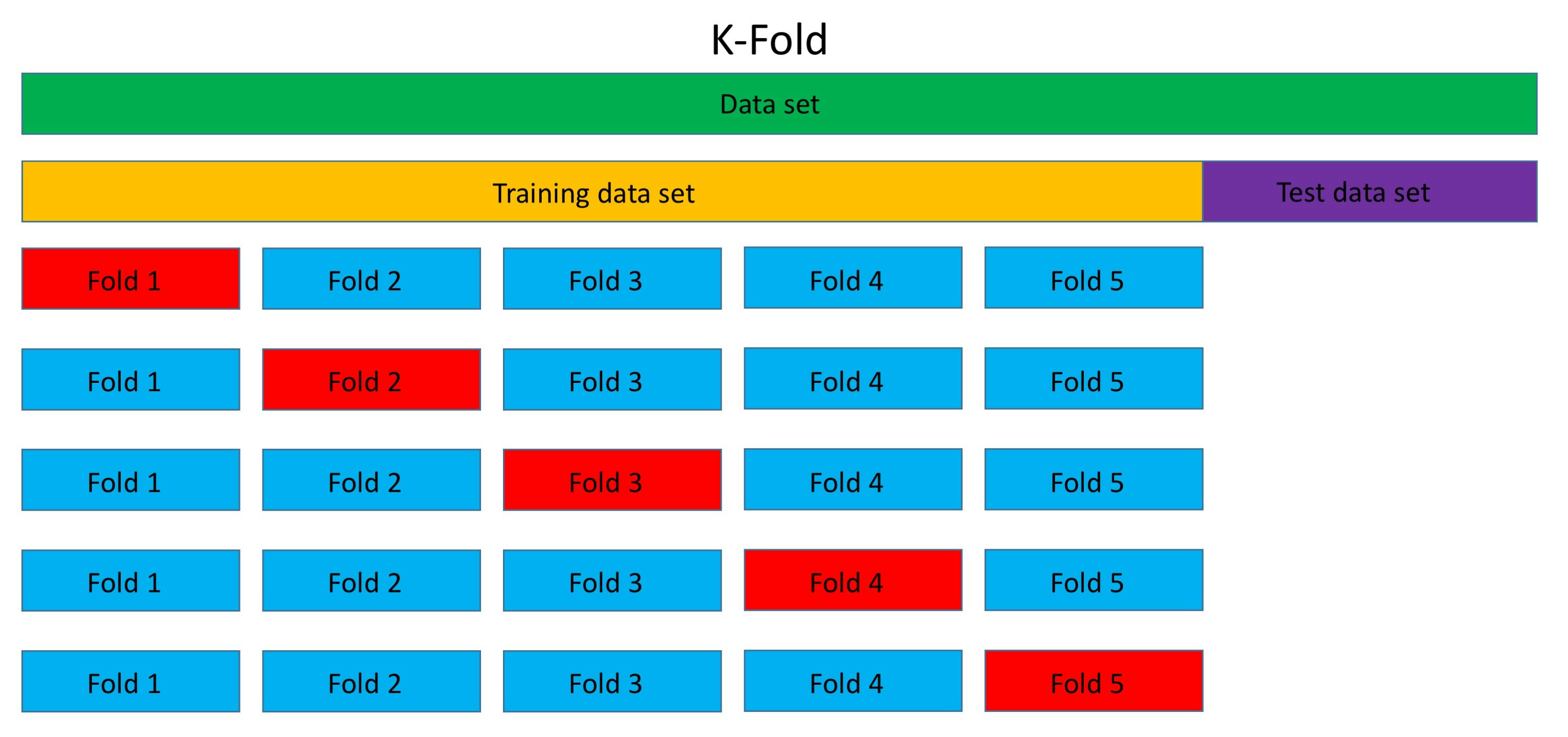
3. K-Fold
K-Foldは、一度学習用データとテスト用データに分けた後、その学習用データをさらに、学習用データとテストデータに分けます。
Hold-outとの大きな違いは学習用データをk分割してk回学習を行わさせることです(下図ではk=5)。k回学習させることで、一部のデータに偏りがあったとしても、k回の学習で偏りを均一化することが出来ます。
K-Foldのメリットデメリットは下記になります。
メリット
・過学習を防ぐことが出来る。
デメリット
・計算量が増えるので、相応のスペックを持つPCが必要
こうしてみると、K-FoldとHold-outのメリットとデメリットはトレードオフの関係になっていることがわかります。
4. 機械学習モデルの構築
両者を比較するために、K-FoldとHold-outで機械学習モデルを構築していきます。
比較に使用したデータですが、scikit-learnにサンプルとして存在するボストン住宅価格データセットを使用しました。
必要なライブラリのインポート
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_boston
from sklearn.model_selection import KFold
from catboost import Pool
from catboost import CatBoost
from sklearn.model_selection import train_test_split
データセットの読み込み
boston = load_boston()
df = pd.DataFrame(boston.data, columns = boston.feature_names)
学習用データセットとテストデータセットの分割
今回は、学習用データ : テストデータ = 7.5 : 2.5 に分割しました。
target = pd.DataFrame(boston.target)
X, Xtest, y, ytest = train_test_split(df, target, random_state = 42, test_size = 0.25)
パラメータの設定
今回はcatboostを用いて評価を行います。Hold-out、K-Fold共に下記のパラメータで設定しました。あまり深くしても精度に違いが現れなかったので、max_depthは、浅めに「5」としています。
params = {
'early_stopping_rounds' : 300,
'loss_function' : 'RMSE',
'num_boost_round' : 20000,
'learning_rate' : 0.01,
'max_depth' : 5,
'verbose' : 200,
'random_seed' : 42,
}
Hold-outのモデル化
preds = np.zeros(Xtest.shape[0])
rmse= []
train_pool = Pool(X, label = y)
model = CatBoost(params)
model.fit(train_pool)
K-Foldのモデル化
続いてK-Foldを使ったcatboostもモデル化していきます。K-Foldで作成したk(=4)モデルの精度について逐次確認します。
preds = np.zeros(Xtest.shape[0])
kf = KFold(n_splits = 4, random_state = 42, shuffle = True)
rmsek= []
n=0
for trn_idx, test_idx in kf.split(X, y):
X_train, X_test = X.iloc[trn_idx], X.iloc[test_idx]
y_train, y_test = y.iloc[trn_idx], y.iloc[test_idx]
train_pool = Pool(X_train, label = y_train)
test_pool = Pool(X_test, label = y_test)
model = CatBoost(params)
model.fit(train_pool, eval_set = [test_pool])
preds += model.predict(Xtest)/kf.n_splits
rmsek.append(mean_squared_error(y_test, model.predict(X_test), squared=False))
print(n+1, rmsek[n])
n+=1
テストデータの予想
始めに分割した時のテストデータを、先ほど構築した機械学習モデルで学習させてtargetとの差を確認していきます。
Hold-out
rmse.append(mean_squared_error(ytest, model.predict(Xtest), squared=False))
print(f"RMSE is {rmse}")
K-Fold
rmse = mean_squared_error(ytest, preds, squared=False)
print(f"RMSE is {rmse}")
5. Hold-outとK-Foldの精度の比較
精度について、今回はRMSE(平均二乗誤差)の評価関数を使用します。ますは、Hold-outの精度について、結果はこちらです。
RMSE is [3.0533076586183814]
続いて、K-Foldの結果はこちらです。
mean RMSE for all the folds is [3.69390918398155, 2.7884670969261487, 2.892018938881272, 4.052458923125346]
RMSE is 3.20902183738405
このように今回はHold-outとK-Foldの精度を比較すると、Hold-outの方が良い精度が出ました。
理由について考察します。
今回使用したデータセットの大きさは、
特徴量の種類数:13
データ数:506
となり、かなり情報量が少なかったことがわかります。
このデータを学習用とテスト用に分けると
学習用:379
テスト用:127
となります。さらにK-Foldを使用するとなると、この379個の学習用データをさらに4分割して計算することになります。
そのため、非常に少ない情報量から機械学習モデルを構築しています。
結果を見てもわかる通り、4ケースでの精度を比較すると、最も良い精度はRMSE = 2.788であるのに対して、最も悪い精度はRMSE = 4.052となっていて、かなりの開きが有ります。
このことから、K-Foldでは根本的にデータ数が少なすぎたため過学習を起こしてモデル全体の精度が悪くなってしまったと考えられます。
この記事の始めでは、「K-Foldの方が過学習が起きにくい」と書いていましたが、今回のようなデータ量が小さい場合だと、逆にK-Foldで過学習が起きてしまう結果となってしまいました。
以上のことから、K-Foldを使用する際は、データ量にも注意する必要があると言えます。
6. 参考文献
[・予測モデルの汎化性能を正確に検証する方法][1]
[1]:https://axa.biopapyrus.jp/machine-learning/model-evaluation/k-fold-cross-validation.html
[・汎化性能][2]
[2]:https://qiita.com/YosukeHoshi/items/927d233408346b41e524
[【データ解析】ボストン住宅価格データセットを使ってデータ解析する][4]
[4]:https://qiita.com/yut-nagase/items/6c2bc025e7eaa7493f89