初回の投稿:https://qiita.com/Yuzunosuke/items/630c65001b5117fef0f0
#前置き
早くもCpawCTFのlevel1をめでたく解き終わりました。
しかし!
ネットワークのパケット解析がテーマのQ11と、ハッシュ関数がテーマのQ12の背景知識の不足を感じました。
ネットワークなんて本当に意味がわかりません。
flagは見つけたものの、今のままじゃQiitaに投稿できるようなまともな記事にならねえ・・・
ですのでちゃんと勉強してから、理解して投稿します。
##環境
Mac OS High sierra 10.13.4
Xcode 9.3.1
ATOM
#Q14を解いてみる
例のごとく問題は飛び飛びで、Q13はありませんでした。
ソートを行うプログラムの作成がメインです。
問題ジャンルのPPCとはProfesional Programming and Codingの略で、コードを書く力が試されるようです。
ソーティングアルゴリズムの実装は大学の講義でも定番です。
私自身も、バブルソート・挿入ソート・マージソート・クイックソート・ヒープソート・計数ソート・基数ソートなど様々なソーティングアルゴリズムを目にしました。
今回は比較的簡単な挿入ソートを用いてflagのゲットを目指します。
##挿入ソートに苦戦する
課題として作ったことあるから余裕余裕
・・・のはずでした。
「前もC言語で書いたし、C言語で大丈夫でしょ」
油断してC言語の難易度を忘れていました。
めちゃくちゃ迷った挙句、最終的に完成したコードがこちらです。
#include <stdio.h>
int main() {
int array[] = {15,1,93,52,66,31,87,0,42,77,46,24,99,10,19,36,27,4,58,76,2,81,50,102,33,94,20,14,80,82,49,41,12,143,121,7,111,100,60,55,108,34,150,103,109,130,25,54,57,159,136,110,3,167,119,72,18,151,105,171,160,144,85,201,193,188,190,146,210,211,63,207};
int i, j, size, temp;
size = sizeof(array) / sizeof(array[0]);
for(i=1; i<size; i++){
j = i;
while((j>0) && (array[j-1] < array[j])){
temp = array[j];
array[j] = array[j-1];
array[j-1] = temp;
j--;
}
}
for(i=0; i<size; i++){
printf("%d",array[i]);
}
printf("\n");
return 0;
}
私が引っかかったのはsizeof演算子です。
###sizeof演算子の罠
C言語はpythonやrubyなどと比べ、プログラミング初心者向きではないと言われていますが、それはその複雑さに起因しています。
しかしそれは汎用性が高く、一般的に難しい操作ができることの裏返しでもあります。
現にC言語はOSの開発や機械制御など様々なところで使用されているようです。そのためC言語はコンピューターのメモリ操作など、表層的とは言えないような部分まで扱えるのです。
今回私がひっかかったsizeof演算子も、単純ではなかったのです・・・
このsizeof演算子は次のように使っています。
sizeof(array)
これで何が取得できるでしょうか。
私は「配列arrayの要素の数が取得できる」と考えていました。
実際にpythonやrubyなどでは似たような具合で配列の要素数を取得することができますね。
C言語を使った今回の場合、sizeof演算子で取得できるのは配列が使っているメモリのサイズなのです。要はこれで取得できるものの単位はbyteなどになります。
私はこれに気づかず、上のように書いて配列arrayのメモリ上でのサイズをひたすら取得していました。
今回は配列の要素の個数を知りたいので
sizeof(array) / sizeof(array[0])
とする必要がありました。
こうすることで、
配列arrayが使っているメモリのサイズ / 配列の中身1つ分のメモリのサイズ
つまり、配列の要素の数が得られます。
この結論に至るまでに1時間ほどかかりました。
本当勘弁してほしい。
flagは無事、ゲットできました。
##Pythonでもやってみる
今回私はC言語で挿入ソートを実装しましたが、CTFでは一般的にはPythonが使われるようです。
そのため、練習としてPythonでも挿入ソートを実装してみます。
array = [15,1,93,52,66,31,87,0,42,77,46,24,99,10,19,36,27,4,58,76,2,81,50,102,33,94,20,14,80,82,49,41,12,143,121,7,111,100,60,55,108,34,150,103,109,130,25,54,57,159,136,110,3,167,119,72,18,151,105,171,160,144,85,201,193,188,190,146,210,211,63,207]
size = len(array)
for i in range(1, len(array)):
j = i
while (j > 0) and (array[j-1] < array[j]):
temp = array[j]
array[j] = array[j-1]
array[j-1] = temp
j -= 1
print(array)
C言語で実装したものを参考にできたので、すぐに完成しました。
PythonはC言語に比べてかなり楽に書けますね。
PythonをATOMというテキストエディタで実装・実行するにあたり、下のサイトを参考にさせていただきました。
https://hajipro.com/python/atom-python
#ソーティングアルゴリズムの色々
今回は挿入ソートというアルゴリズムを用いて並び替えを行いました。
ソーティングアルゴリズムには様々なものがあり、
http://sorting.at/
のようなサイトでは
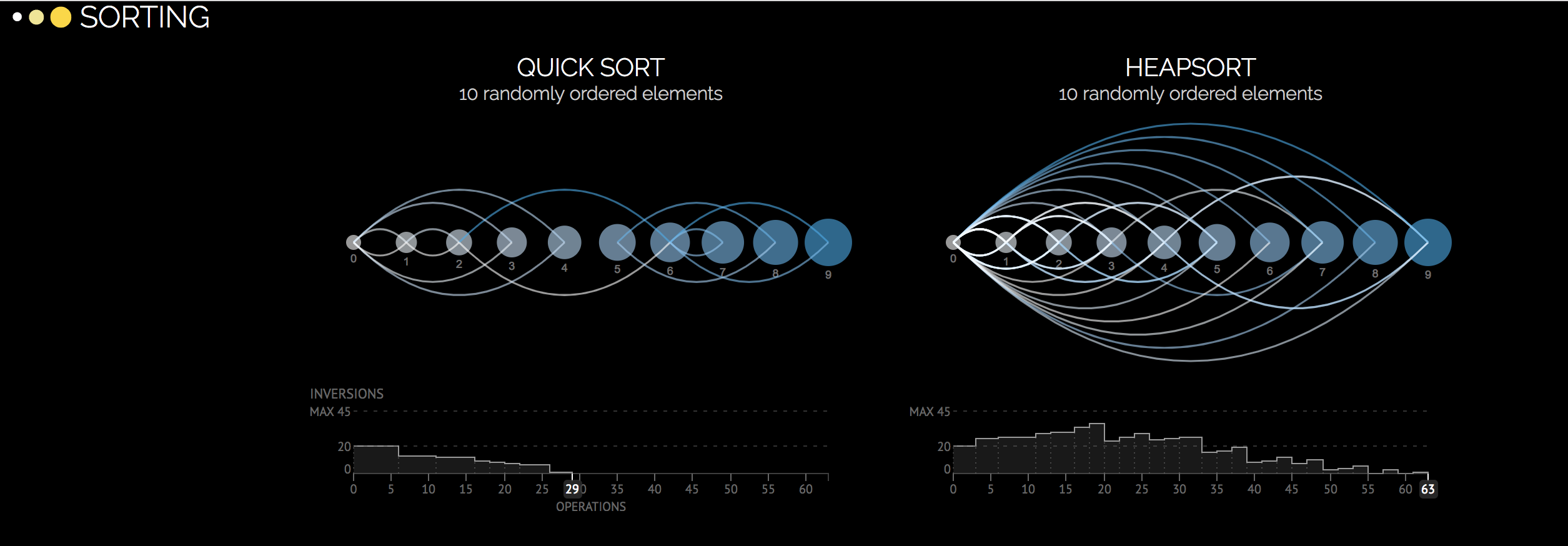
このように、その違いなどをわかりやすく見ることができます。
その中で一番重視される"違い"は、実行時間でしょう。
ちゃんと並び替えてくれるけどめちゃくちゃ遅い、では現実的に使い物にならないわけです。
##早い方が良いよね
もちろん早く並び替えができる方が嬉しいわけで、そのために色々なアルゴリズムが存在します。
それらのアルゴリズムがどのようなもので、何が早いのか、などは上で紹介したようなサイトを見ればすぐにわかります。
私が大学の講義で一番苦戦したのは、実行時間の表し方です。
##実行時間を表すのは大変
ソーティングアルゴリズムの実行時間は、並び替えるものの数で決定します。
今回の問題のように、挿入ソートを用いた場合を考えます。
並び替える配列arrayの要素数がn個だったとすると、その実行時間は
O(n^2)
という風に表されるようです。
挿入ソートは、どこか1つの数字を持ってそれを隣の数と比べて入れ替える、といった操作をします。そしてその入れ替える操作をする回数が増えれば増えるほど、全体の実行時間も増えてしまいます。
上で示した表し方はその入れ替わりが、最悪nの2乗回くらい起きてしまうということを表しています。
もしも並び替える数字の数が2倍になったら、かかる時間は4倍に。10倍になったら100倍かかってしまう。
ということでしょうか。
恐ろしいです・・・。
#並び替えは大事
今回は並び替える数字の数がそれほど多くなかったため、挿入ソートでも充分でした。しかし、本来ならばどのアルゴリズムを使うべきなのかをもっと吟味する必要があったのでしょう。
奥が深い・・・。