#Pythonで学ぶ制御工学< ゲインチューニング(モデルマッチング) >
はじめに
基本的な制御工学をPythonで実装し,復習も兼ねて制御工学への理解をより深めることが目的である.
その第18弾として「ゲインチューニング(モデルマッチング法)」を扱う.
チューニング
前回(https://qiita.com/Yuya-Shimizu/items/5a8c15edfaf3aa80c542 ),ゲインチューニングの方法の1つとして限界感度法について学んだ.今回は,モデルマッチング法というゲインチューニング方法について学習する.
モデルマッチング法
以下では,モデルマッチング法について簡単にまとめたものを示す.

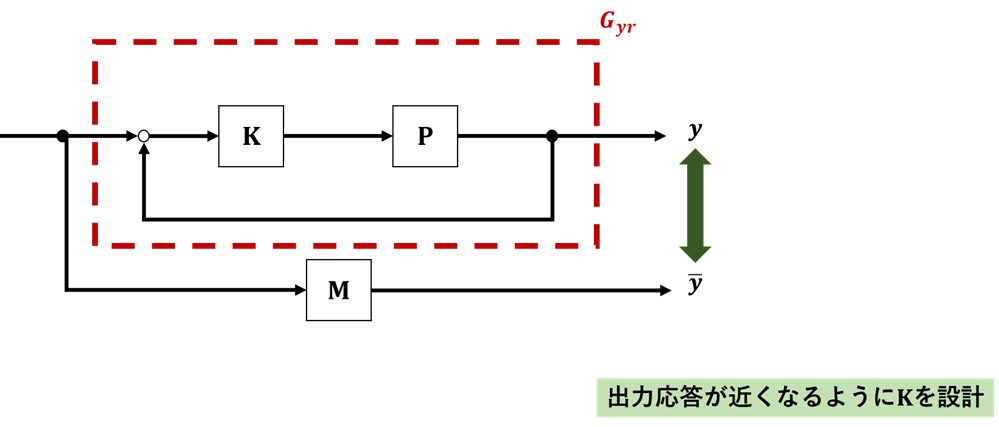

ここでは,前回同様アームの角度制御を例に,PI-D制御とI-PD制御をもってモデルマッチング法を適用する.


実装
先ほどの説明にしたがって,ゲインチューニングを行う.以下では,マクローリン展開,規範モデルとの比較によるPIDゲイン特定,およびモデルマッチングという3つのプログラムについて,それぞれソースコードとそのときの出力を示す.
ソースコード:マクローリン展開
"""
2021/03/17
@Yuya Shimizu
マクローリン展開
"""
import sympy as sp
# 文字の定義
s = sp.Symbol('s')
kp, kd, ki = sp.symbols('k_p k_d kj_i')
Mgl, mu, J = sp.symbols('Mgl mu J')
sp.init_printing()
Mc = {} #結果を格納する辞書型配列
# PI-D
G = (kp*s+ki)/(J*s**3 + (mu+kd)*s**2 + (Mgl+kp)*s +ki)
Mc['PI-D'] = sp.series(1/G, s, 0, 4) #3次の項まで展開
# I-PD
G = (ki)/(J*s**3 + (mu+kd)*s**2 + (Mgl+kp)*s +ki)
Mc['I-PD'] = sp.series(1/G, s, 0, 4) #3次の項まで展開
for M in Mc:
print(f"<{M}>\n{Mc[M]}\n\n")
出力
<PI-D>
1 + s**2*(-Mgl*k_p/kj_i**2 + k_d/kj_i + mu/kj_i) + s**3*(J/kj_i + Mgl*k_p**2/kj_i**3 - k_d*k_p/kj_i**2 - k_p*mu/kj_i**2) + Mgl*s/kj_i + O(s**4)
<I-PD>
J*s**3/kj_i + s**2*(k_d/kj_i + mu/kj_i) + s*(Mgl/kj_i + k_p/kj_i) + 1
整理することで,上での説明にあった式と一致する.
ソースコード:規範モデルとの比較によるPIDゲイン特定
"""
2021/03/17
@Yuya Shimizu
kp, ki, kdを求める
"""
import sympy as sp
# 文字の定義
z, wn = sp.symbols('zeta omega_n')
a1, a2 = sp.symbols('alpha1 alpha2')
kp, kd, ki = sp.symbols('k_p k_d k_i')
Mgl, mu, J = sp.symbols('Mgl mu J')
sp.init_printing()
solution = {} #結果を格納する辞書型配列
# PI-D & 2-dimention
f1 = Mgl/ki - 2*z/wn
f2 = (mu+kd)/ki - Mgl*kp/(ki**2) - 1/(wn**2)
f3 = J/ki - kp*(mu+kd)/(ki**2) + Mgl*kp**2/(ki**3)
solution['PI-D & 2-dimention'] = sp.solve([f1, f2, f3], [kp, kd, ki])
# PI-D & 3-dimention
f1 = Mgl/ki - a1/wn
f2 = (mu+kd)/ki - Mgl*kp/(ki**2) - a2/(wn**2)
f3 = J/ki - kp*(mu+kd)/(ki**2) + Mgl*kp**2/(ki**3) - 1/(wn**3)
solution['PI-D & 3-dimention'] = sp.solve([f1, f2, f3], [kp, kd, ki])
# I-PD & 2-dimention
f1 = (Mgl+kp)/ki - 2*z/wn
f2 = (mu+kd)/ki - 1/(wn**2)
f3 = J/ki
solution['I-PD & 2-dimention'] = sp.solve([f1, f2, f3], [kp, kd, ki])
# I-PD & 3-dimention
f1 = (Mgl+kp)/ki - a1/wn
f2 = (mu+kd)/ki - a2/(wn**2)
f3 = J/ki - 1/(wn**3)
solution['I-PD & 3-dimention'] = sp.solve([f1, f2, f3], [kp, kd, ki])
for S in solution:
print(f"<{S}>\n{solution[S]}\n\n")
出力
<PI-D & 2-dimention>
[(J*omega_n**2, 2*J*omega_n*zeta + Mgl/(2*omega_n*zeta) - mu, Mgl*omega_n/(2*zeta))]
<PI-D & 3-dimention>
[((J*alpha1*omega_n**2 - Mgl)/(alpha1*alpha2), J*alpha1*omega_n/alpha2 - Mgl/(alpha2*omega_n) + Mgl*alpha2/(alpha1*omega_n) - mu, Mgl*omega_n/alpha1)]
<I-PD & 2-dimention>
[]
<I-PD & 3-dimention>
{k_p: J*alpha1*omega_n**2 - Mgl, k_d: J*alpha2*omega_n - mu, k_i: J*omega_n**3}
I-PD制御において,2次系規範モデルではPIDゲインが計算できないようだ.
ソースコード:モデルマッチング
"""
2021/03/17
@Yuya Shimizu
モデルマッチング(2次規範モデル)- アームの角度制御
"""
import numpy as np
import matplotlib.pyplot as plt
from control import tf
from control.matlab import step
from for_plot import plot_set
# マッチング法を適用するクラス
class Matching():
"""P-IDかI-PDをGに,規範モデルの次元をdimに指定できる"""
def __init__(self, G, dim):
self.omega_n = 15
if dim == 2:
self.zeta = 0.707 #バターワース(二項係数標準形でも構わない)
elif dim == 3:
self.alpha = [3, 3] #二項係数標準形(他のでもよいがこれが性能がよかった)
self.G = G
self.dim = dim
#パラメータ設定
self.g = 9.8 #重力加速度[m/s^2]
self.l = 0.2 #アームの長さ[m]
self.M = 0.5 #アームの質量[kg]
self. mu = 1.5e-2 #粘性摩擦係数[kg*m^2/s]
self.J = 1.0e-2 #慣性モーメント[kg*m^2]
#目標値(指示値=refference)
self.ref = 30 #目標角度30[deg]
##実行
self.model()
self.matching()
#規範モデル
def model(self):
if self.dim == 2:
self.Msys = tf([0, self.omega_n**2], [1, 2*self.zeta*self.omega_n, self.omega_n**2])
elif self.dim == 3:
self.Msys = tf([0, self.omega_n**3], [1, self.alpha[1]*self.omega_n, self.alpha[0]*self.omega_n**2, self.omega_n**3])
#モデルマッチング
def matching(self):
simT = np.arange(0, 2, 0.01)
if self.G == 'PI-D':
if self.dim == 2:
kp = self.omega_n**2*self.J
ki = self.omega_n*self.M*self.g*self.l/(2*self.zeta)
kd = 2*self.zeta*self.omega_n*self.J + self.M*self.g*self.l/(2*self.zeta*self.omega_n) - self.mu
elif self.dim == 3:
kp = (self.J*self.alpha[0]*self.omega_n**2 - self.M*self.g*self.l)/(self.alpha[0]*self.alpha[1])
ki = self.M*self.g*self.l*self.omega_n/self.alpha[0]
kd = self.J*self.alpha[0]*self.omega_n/self.alpha[1] - self.M*self.g*self.l/(self.alpha[1]*self.omega_n) + self.M*self.g*self.l*self.alpha[1]/(self.alpha[0]*self.omega_n) - self.mu
else:
print("can't calculate $k_P$, $k_I$, $k_D$ by matching with {self.dim}-dim model")
return
Gyr = tf([kp, ki], [self.J, self.mu+kd, self.M*self.g*self.l+kp, ki])
elif self.G == 'I-PD':
if self.dim == 3:
kp = self.J*self.alpha[0]*self.omega_n**2 - self.M*self.g*self.l
ki = self.J*self.omega_n**3
kd = self.J*self.alpha[1]*self.omega_n - self.mu
else:
print(f"can't calculate $k_P$, $k_I$, $k_D$ by matching with {self.dim}-dim model")
return
Gyr = tf([0, ki], [self.J, self.mu+kd, self.M*self.g*self.l+kp, ki])
#シミュレーション
yM, tM = step(self.Msys, simT)
y, t = step(Gyr, simT)
#描画
fig, ax = plt.subplots()
ax.plot(tM, yM*self.ref, label = 'M')
ax.plot(t, y*self.ref, label = 'Gyr')
plot_set(ax, 't', 'y', 'best')
ax.set_title(f"{self.G} & {self.dim}-dimention model")
plt.show()
if __name__=='__main__':
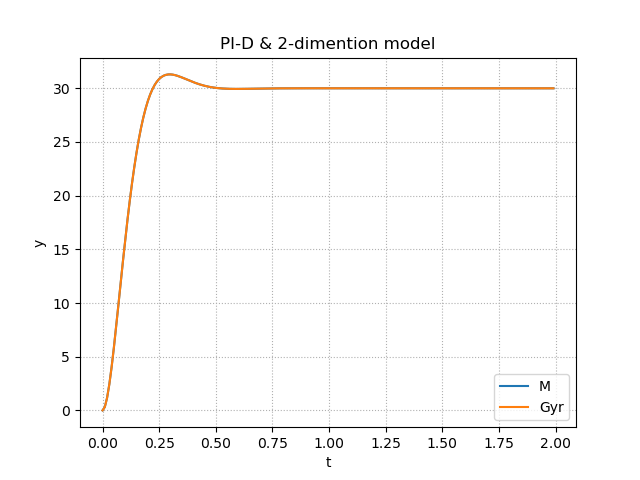
Match = Matching('PI-D', 2) #PI-D, 2-dimention
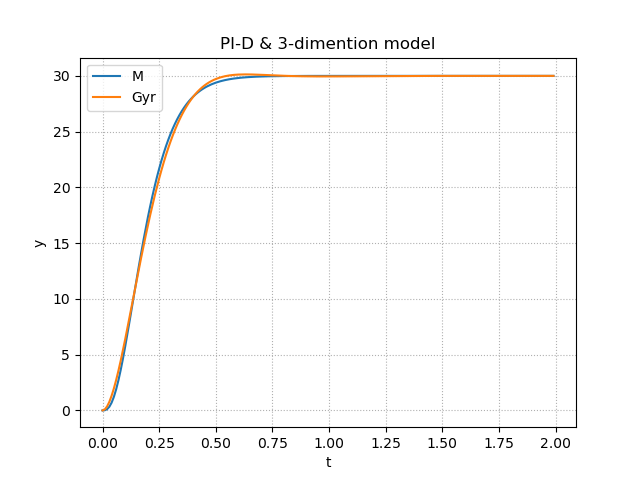
Match = Matching('PI-D', 3) #PI-D, 3-dimention
Match = Matching('I-PD', 2) #I-PD, 2-dimention
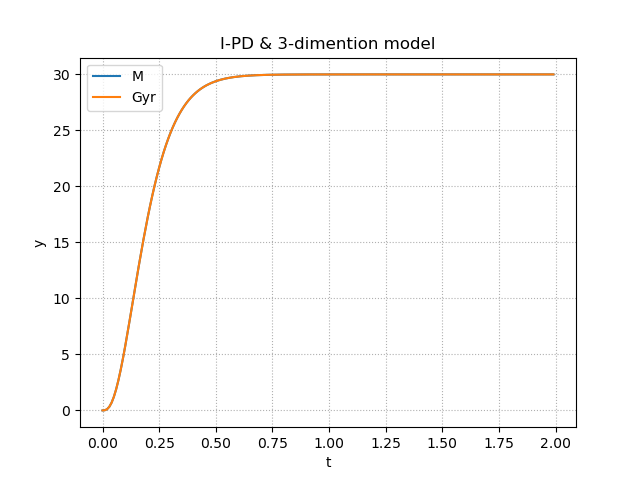
Match = Matching('I-PD', 3) #I-PD, 3-dimention
出力
can't calculate kp, ki, kd by matching with 2-dim model
考察
完璧に規範モデルに一致しているものもあれば,そうでないものもある.同じ制御対象でも制御器によって,好まれる規範モデルがあり,二項係数標準形なのかどうかという部分でも挙動が変わっていたことから,幾つかの組み合わせの中から最もうまく規範モデルに近づくものを選んであげるとよいと思われる.
感想
前回に引き続きゲインチューニングを学んだ.制御器を設計する際に重要になってくる部分である.設計するときには,このあたりもヒントにできたらと思う.
今回は,少しクラスの定義もしてみた.それほど汎用性はないが,プログラムのカプセル化により,個人的に理解しやすい形にはできた.
参考文献
Pyhtonによる制御工学入門 南 祐樹 著 オーム社