Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@Yuya-Shimizu(清水 優椰)

Pythonで学ぶアルゴリズム　第14弾：3目並べ（ox問題）

Last updated at Posted at 2021-01-05

#Pythonで学ぶアルゴリズム< 3目並べ（ox問題） >

##はじめに
基本的なアルゴリズムをPythonで実装し，アルゴリズムの理解を深める．
その第14弾として3目並べ（ox問題）を扱う．

##3目並べ（ox問題）
$3\times3$のマスにo, xを交互に配置し，先に3つ縦・横・斜めのいずれかに並べることが勝利条件となる．
プログラムへ実行する際には数値として扱う必要がある．まず，各マスを次のように考える．

image.png

A~Iの順番で9桁の2進数で表現する．例として，oが勝利条件を満たすときの配列とそれらに対応する2進数を次の図に示す．
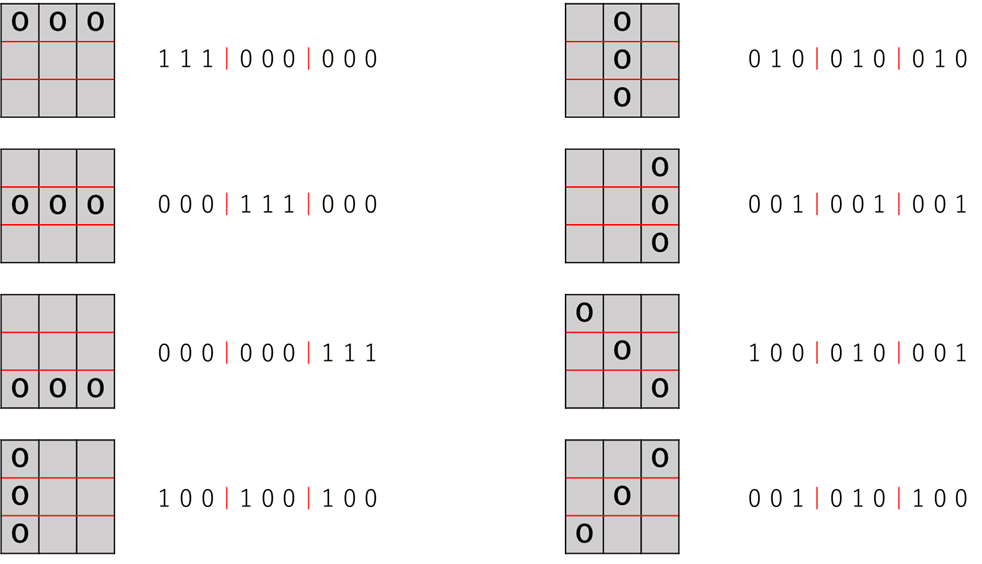
image.png
上記のように，$3\times3$では，8通りの勝利条件がある．

勝利条件を満たす前にすべてのマスが埋められてしまった場合，引き分けとなる．これらの勝利条件と引き分けを終了条件として，繰り返し交互にoとxを配置していく．今回はコンピュータ同士が乱数に従い勝負することを考える．次に実装コードとそのときの出力を示す．また可視化についても試みた．

##実装
次に示すプログラムでは，先ほどの説明にあった9桁の2進数でoとxの配置を表現する．

#####コード

tick_tac_toe1.py
"""
2021/01/02
@Yuya Shimizu

3目並べ
"""
import random

#勝利条件
#上段3列，中段3列，下段3列，左端3行，中央3行，右端3行，右下斜め，右上斜め
finish = [
                0b111000000, 0b000111000, 0b000000111, 0b100100100,
                0b010010010, 0b001001001, 0b100010001, 0b001010100
            ]

#勝利判定
def check(player):
    for mask in finish:
        if player == mask:
            return  True
    return False

#交互にoとxを置く
def play(player1, player2):
    if check(player2):
        print([bin(player1), bin(player2)])
        return  #終了

    board = player1 | player2

    if board == 0b111111111:    #すべてのマスが埋まっているなら引き分けで終了
        print([bin(player1), bin(player2)])
        return  #終了

    #置ける場所を探す
    putable = [i for i in range(9) if (board & (1 << i)) == 0]
    #ランダムに置いてみる
    r = random.choice(putable)
    
    play(player2, player1 | (1 << r))   #再帰

if __name__ == '__main__':
    play(0,0)   #初期状況を与える; いまだと，両プレイヤがどちらも置いていないという状況

#####出力

['0b110001010', '0b1110101']

次にボードの状況を可視化するプログラムコードと出力を示す．

tick_tac_toe1_1.py
"""
2021/01/02
@Yuya Shimizu

3目並べ（可視化）
"""
import random

#勝利条件
#上段3列，中段3列，下段3列，左端3行，中央3行，右端3行，右下斜め，右上斜め
finish = [
                0b111000000, 0b000111000, 0b000000111, 0b100100100,
                0b010010010, 0b001001001, 0b100010001, 0b001010100
            ]

#ゲームボードの初期化　　'* 'は空欄を表している
Board = {
        'turn':'turn : 1 \n\n',
        1:'* ', 2:'* ', 3:'* ', 'z1':'\n',
        4:'* ', 5:'* ', 6:'* ', 'z2':'\n',
        7:'* ', 8:'* ', 9:'* '
        }

#可視化関数
def draw(player1, player2, turn):
    show_board = "" #出力データ(文字)を格納する変数を初期化

    #turn(奇数)がplayer1，turn(偶数)がplayer2
    #0 turnのみstartとする
    if turn % 2 == 1 and turn != 0:
        Board['turn'] = f"\n\nturn : {turn}  (player1) \n"
        #ボード1をplayer2，ボード2をplayer1 (これは引数のplayerがturn毎にに入れ替わるため)  
        board1 = str(bin(player2))[2:]
        board2 = str(bin(player1))[2:]
    elif turn % 2 == 0 and turn != 0:
        Board['turn'] = f"\n\nturn : {turn}  (player2) \n"
        #ボード1をplayer1，ボード2をplayer2 (これは引数のplayerがturn毎にに入れ替わるため)  
        board1 = str(bin(player1))[2:]
        board2 = str(bin(player2))[2:]
    else:
        Board['turn'] = f"\n\nstart \n"
        #ボードは適当．エラーを出さないようにしているだけ．それ以外の意味はない
        board1 = str(bin(player1))[2:]
        board2 = str(bin(player2))[2:]
        
    #player1(o)の配置をゲームボードへ反映
    for i in range(1, len(board1)+1):
        if  board1[-i] == '1' and Board[10-i] == '* ':
            Board[10-i] = 'o '
    #player2(x)の配置をゲームボードへ反映
    for i in range(1, len(board2)+1):
        if board2[-i] == '1' and Board[10-i] == '* ':
            Board[10-i] = 'x '

    #更新されたゲームボード可視化のための文字配列を生成
    for i in Board:
        show_board += Board[i]

    #可視化
    print(show_board)

#勝利判定
def check(player):
    for mask in finish:
        if player & mask == mask:
            return  True
    return False

#交互にoとxを置く
def play(player1, player2, turn = 0):
    result = draw(player1, player2, turn)   #毎ターンの状況を可視化

    #勝利判定
    if check(player2):
        #turn(奇数)で終了したらplayer1の勝利 
        if turn % 2 == 1:
            print(f"player1 WIN")
            return  #終了
        
        #turn(偶数)で終了したらplayer2の勝利 
        else:
            print(f"player2 WIN")
            return  #終了

    board = player1 | player2       #o, xの配置されたボード状況を生成
    if board == 0b111111111:    #すべてのマスが埋まっているなら引き分けで終了
        print(f"DRAW")
        return  #終了
    
    #置ける場所を探す
    putable = [i for i in range(9) if (board & (1 << i)) == 0]
    #ランダムに置いてみる
    r = random.choice(putable)
    
    turn += 1   #turnの追加
    
    play(player2, player1 | (1 << r), turn = turn)  #再帰(turnを重ねる) 

if __name__ == '__main__':
    play(0,0)   #初期状況を与える; いまだと，両プレイヤがどちらも置いていないという状況

#####出力

start 
* * * 
* * * 
* * * 


turn : 1  (player1) 
* * * 
* * o 
* * * 


turn : 2  (player2) 
* * x 
* * o 
* * * 


turn : 3  (player1) 
* * x 
* * o 
* o * 


turn : 4  (player2) 
* * x 
* x o 
* o * 


turn : 5  (player1) 
* o x 
* x o 
* o * 


turn : 6  (player2) 
* o x 
x x o 
* o * 


turn : 7  (player1) 
* o x 
x x o 
* o o 


turn : 8  (player2) 
* o x 
x x o 
x o o 
player2 WIN

##感想
また後日共有するナップサック問題にもあるが，2進数を用いてある状況を表現することに慣れてきた気がする．また再帰にも少し慣れてきて，再帰の際にはreturnで何かを返すとNoneとなってしまい，表示させるためにはprintを使う必要があることも分かった．今回は可視化にも挑戦した．可視化は少し苦労してしまった．その要因は再帰の際に引数を入れ替えていることであった．そのため，はじめはoだけになってしまったり，うまく表示されなかったりした．また，ボードを可視化するにあたって，プレイヤがもつ配置条件とボードの配置の対応付けが逆転していたため，for文では-iや10-iなど末尾からや差で配列操作をする必要があった．何とか自力で可視化することができた．もう少しまとめられそうだなとは思ってはいるが，3目並べのアルゴリズムとそれの実装については学ぶことができたのではないかと思う．

##参考文献
Pythonで始めるアルゴリズム入門　伝統的なアルゴリズムで学ぶ定石と計算量
　　　　　　　　　　　　　　　　　　　　　　　　 増井 敏克　著　　翔泳社

0
3
4

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?