はじめに
今回私は最近はやりのchatGPTに興味を持ち、深層学習について学んでみたいと思い立ちました!
深層学習といえばPythonということなので、最終的にはPythonを使って深層学習ができるとこまでコツコツと学習していくことにしました。
ただ、勉強するだけではなく少しでもアウトプットをしようということで、備忘録として学習した内容をまとめていこうと思います。
この記事が少しでも誰かの糧になることを願っております!
※投稿主の環境はWindowsなのでMacの方は多少違う部分が出てくると思いますが、ご了承ください。
最初の記事:Python初心者の備忘録 #01
前の記事:Python初心者の備忘録 #13 ~統計学入門編03~
次の記事:Python初心者の備忘録 #15 ~機械学習入門編01~
本記事は統計的仮説検定についてまとめてあります。
■学習に使用している資料
Udemy:米国データサイエンティストが教える統計学超入門講座【Pythonで実践】
■統計的仮説検定
▶統計的仮説検定とは
- 統計的に仮説が正しいか確かめるもので、意思決定を左右する重要な役割を果たす
例:ある施策により来店者数は増えたか -> 「本当に施策の効果か、たまたま増えただけじゃない?」ということを統計的に確認する - Z検定、カイ二乗検定、t検定、等分散の検定、正規性の検定など、色々な検定が存在する
▶帰無仮説(null hypothesis)と対立仮説(alternative hypothesis)
- 検定ではまず仮説を立てる必要があり、その仮説が統計的に成立するか¥といえるかを検証する
- 仮説の立て方には帰無仮説と対立仮説があり、立てた仮説が正しければそのまま、正しくなければ仮説を棄却し、反対の仮説を成立させる方法
- 帰無仮説:棄却することを狙った仮説(薬Aと薬Bには差はない)
- 対立仮説:成立することを狙った仮説(薬Aと薬Bには差がある) - その名の通り帰無仮説と対立仮説は対立の関係にあり、片方が成立しなければもう片方が成立するという形となる
- 対立仮説には、両側検定(a≠b)と片側検定(a>b or a<b)がある
なぜ帰無仮説が必要なのか?
「差がある」といっても様々な差が存在し、どの「差」にフォーカスして仮説を立てるのかを考えると膨大な量になってしまう。
しかし、「差がない」は1つに定まるのでこちらを棄却して「差がある」ことを証明するほうが簡単、ということになる。
※数学の背理法みたいな感じ
■比率差の検定(Z検定)
▶比率差の検定とは
- 2群の比率に差があるかを検定する
- 検定で使用する比率は標本比率だが、差があるかどうかはあくまで「母比率が」を見ているので注意
比率差の検定の大まかな流れは下記のようになる
例:A/Bテスト
従来施策A:閲覧数1000回中、クリック数30回(3.0%:$p_1$)
新施策B:閲覧数1000回中、クリック数33回(3.3%:$p_2$)
-> クリック数の差は「偶然じゃない」、または「偶然である」ということを言いたい
仮説
- 帰無仮説:AとBに差はない($p_1$=$p_2$)
- 対立仮説:AよりBのほうがクリック比率が大きい($p_1$<$p_2$)
※帰無仮説が棄却された場合「$p_1$>$p_2$」の可能性も残っているが、対立仮説には成立させたい方を設定すればいい
標本観察
帰無仮説が正しいという仮定のもと、標本の観察を行う
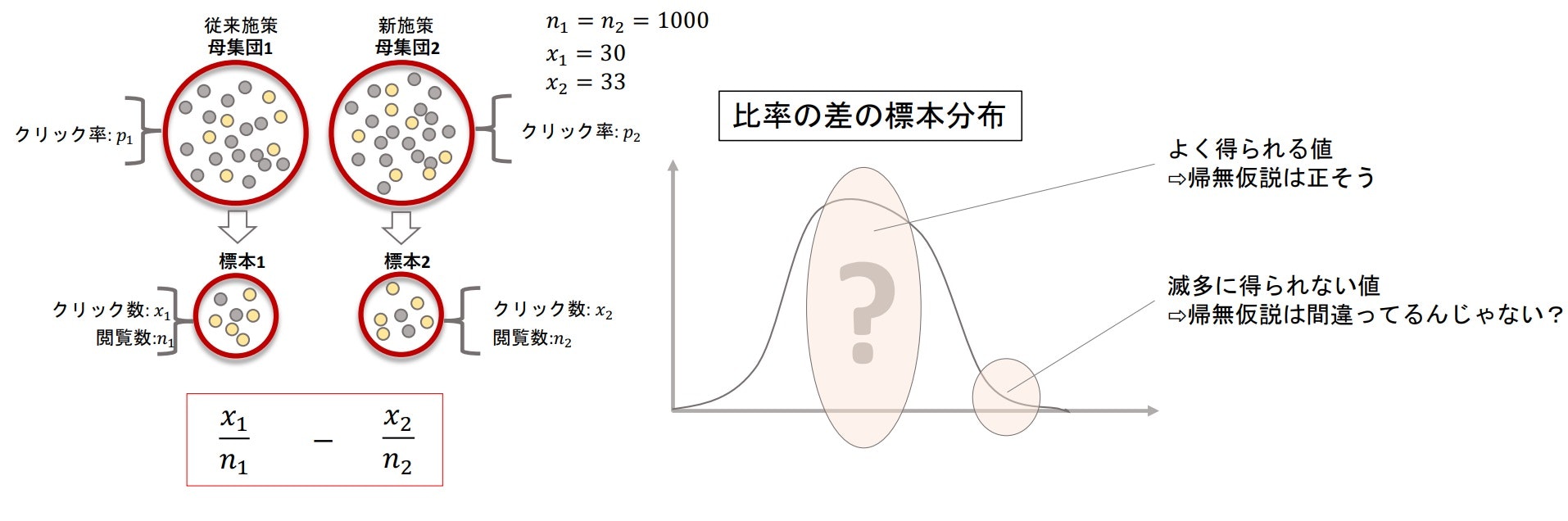
- それぞれの標本の比率から比率の差がどのような標本分布になるか考える
- 帰無仮説が正しいとした場合、比率の差がどのくらいの確率で得られるかを確認する
- 比率の差の標本分布において、得られた差がよく出る値なら「帰無仮説が正しそう」、逆にめったに得られない値ならば「帰無仮説はおかしい」と考えることができる
比率の差の標本分布
まず、比率の標本分布は下記のようになる。
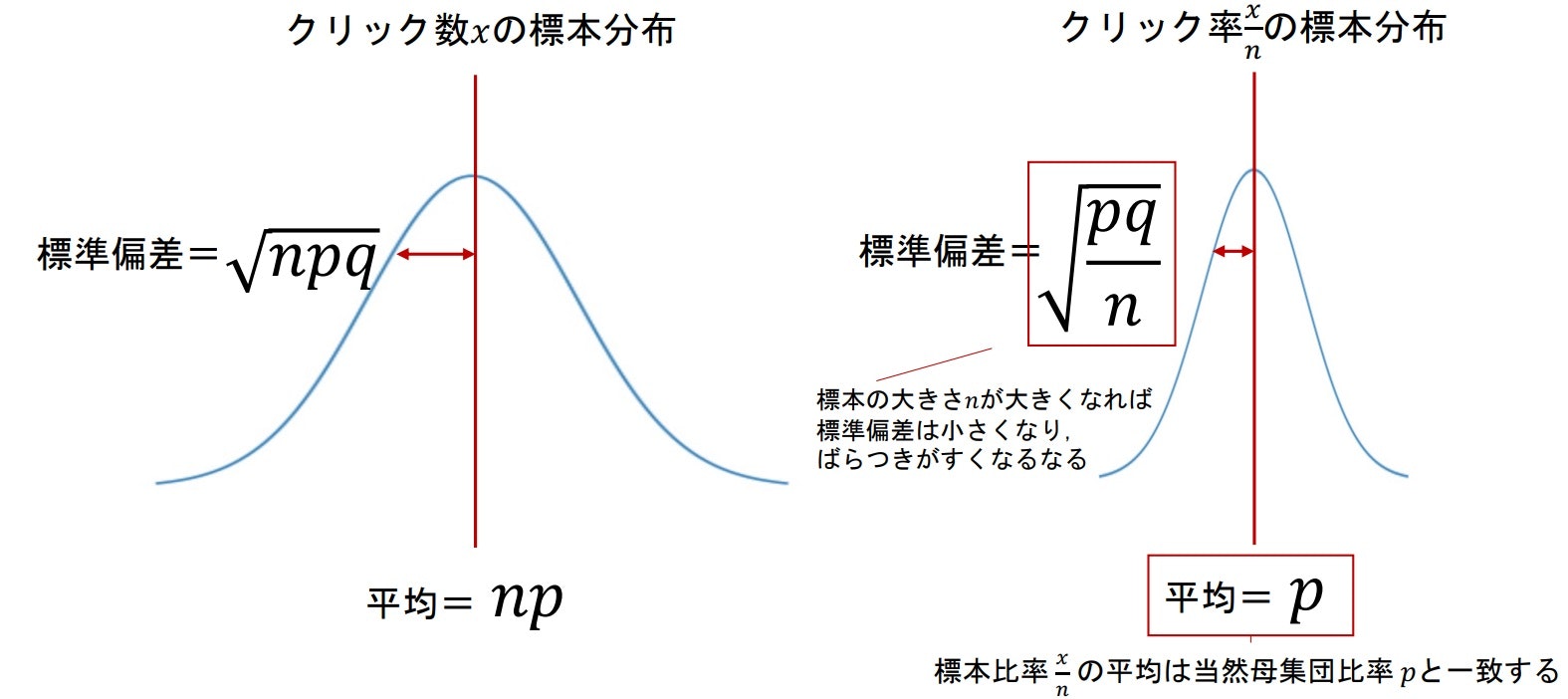
次に2つの確率変数の差は下記のようになる
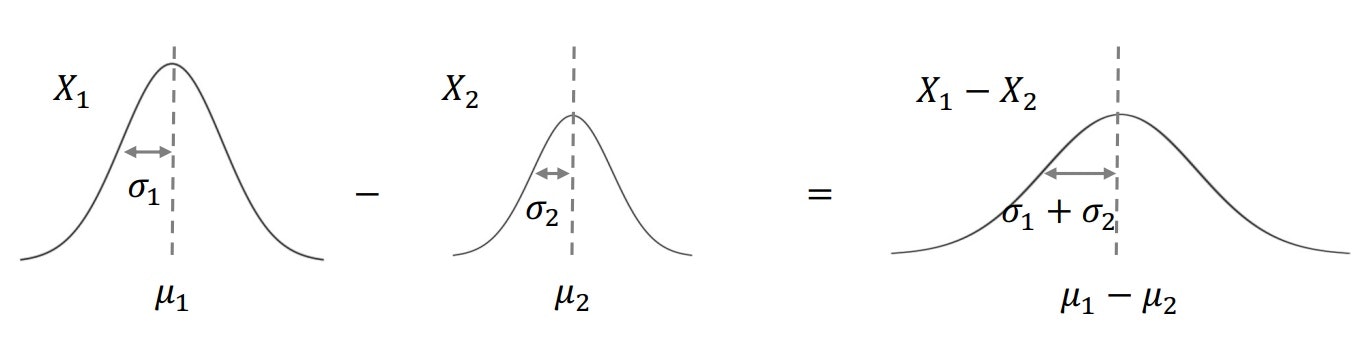
以上のことから、2群の比率の差($\frac{x_1}{n_1}-\frac{x_2}{n_2}$)の標本分布では平均pは2群の差($p_1-p_2$) となり、分散($\frac{pq}{n}$)は2群の和($\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}$) となる。
※分散が2群の和になるのは、2群の差が負の数になったとしても2乗して正の値になるから
帰無仮説が正しいと仮定したときの比率差の標本分布
「比率差はない」ことから「$p_1=p_2$」となるので、比率差の標本分布に当てはめると下記のようになる。
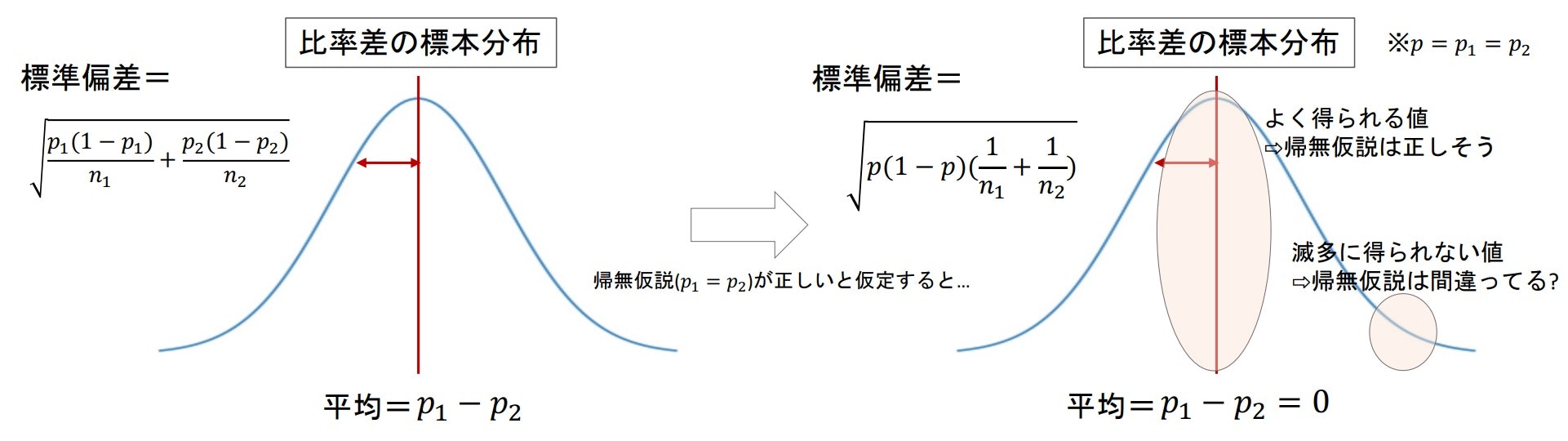
この比率差の標本分布($p_1=p_2$)から実際に得られた値($\frac{x_1}{n_1}-\frac{x_2}{n_2}$)がよく得られる値かどうかを考える。
※この時、帰無仮説を棄却するかどうかの境目を設定する必要がある -> 有意水準
▶有意水準(α)とは
- 帰無仮説を正しいとした際にめったに起きない確率の基準のことで、基準外の領域を棄却域という
- 通常はα=0.05、またはα=0.01
- 帰無仮説が棄却されたとき「統計的に有意である」と表現する
- 両側検定と片側検定で棄却域の取り方が若干異なる
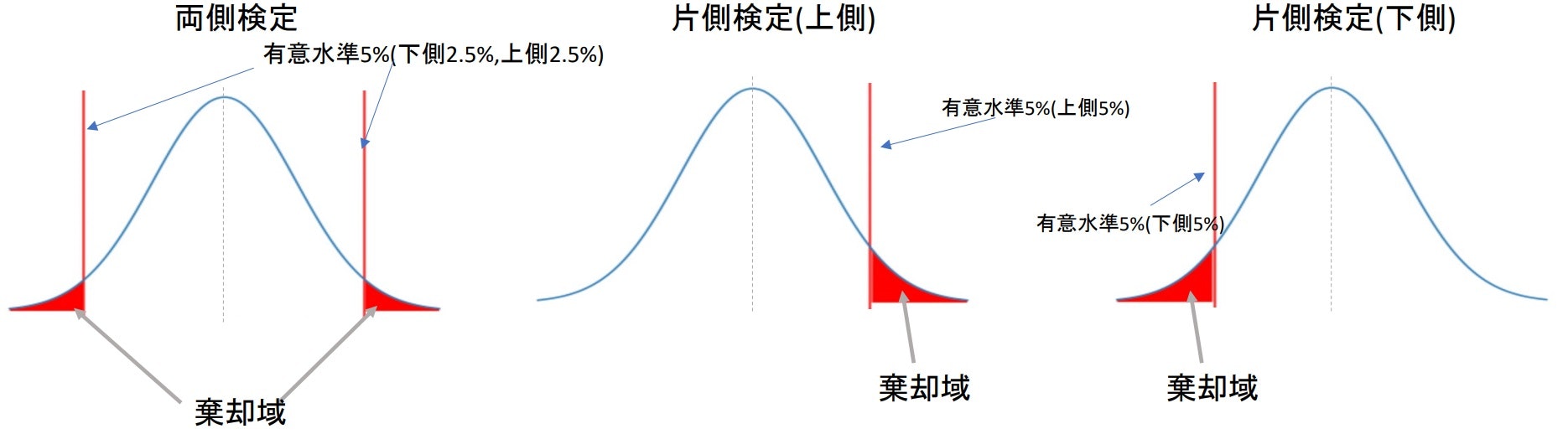
※今回であれば$p_1<p_2$($p_1-p_2<0$)なので、片側検定(下側)の棄却域について考えればいい
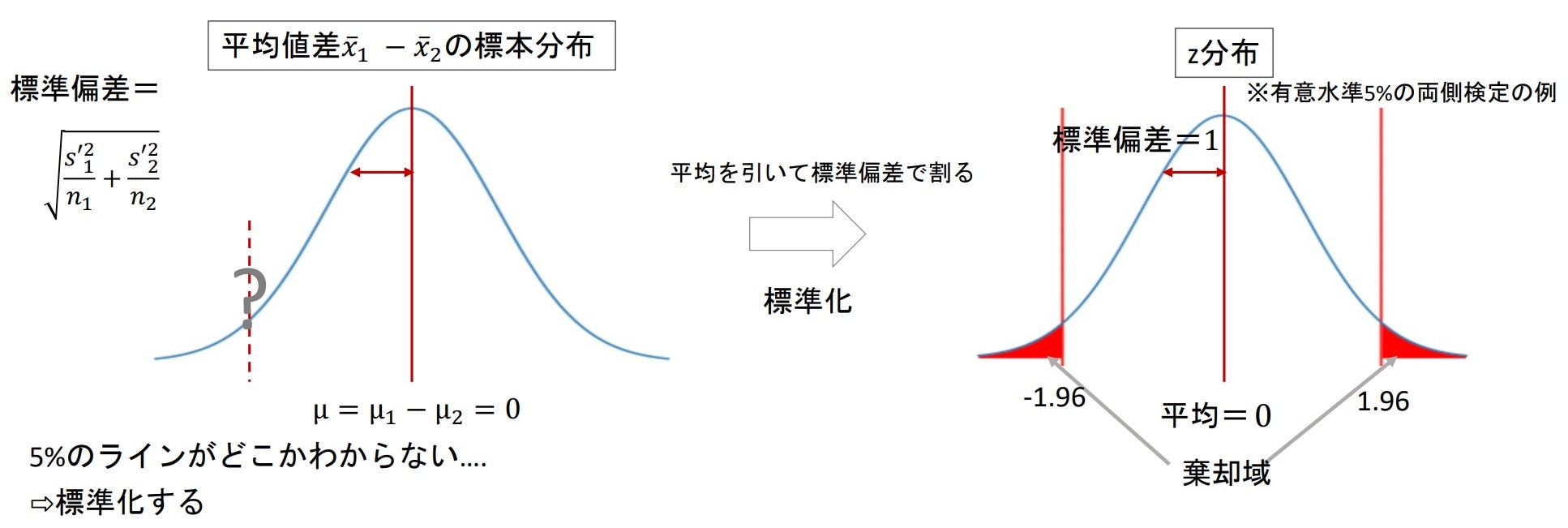
▶比率差の標本分布の標準化
- いつも通り扱いやすくするために標準化を行う
- 有意水準5%とは95%信頼区間の逆と考えられるので、両側検定なら-1.96~1.96の外側と考えることができる
- 片側検定の場合は-1.64、または1.64の外側となる
標準化の式は下記のようになる
$z=\frac{\frac{x_1}{n_1}-\frac{x_2}{n_2}}{\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}}$
※母集団の母比率pが必要なので、推定値$\hat{p}$について考える
▶母比率pの推定値
- 2つの標本を合わせた比率を母比率の推定値$\hat{p}$とする
$\hat{p}=\frac{x_1+x_2}{n_1+n_2}$ - 上記の$\hat{p}$を標準化の式zのpに適用する
今回の場合
A:$n_1=1000$、$x_1=30$
B:$n_2=1000$、$x_2=33$
$\hat{p}=\frac{30+33}{1000+1000}=\frac{63}{2000}$
$z=\frac{\frac{30}{1000}-\frac{33}{1000}}{\sqrt{\frac{63}{2000}(1-\frac{63}{2000})(\frac{1}{1000}+\frac{1}{1000})}}=-0.38$
-> 有意水準5%の-1.64の内側なので、帰無仮説は正しいということになる。
※帰無仮説が正しいと仮定したとき、検定統計量より極端な値(今回であれば-0.38)が得られる確率のことをp値という
-> つまり、p値<α、またはp値>αの時に帰無仮説は棄却できる。
補足
今回の例では帰無仮説を棄却できなかったが、これは「差がない」=「値は同じ」ということを証明することにはつながらず、あくまで「差がないことを"否定できない"」、ということになることに注意
statsmodels.stats.proportion.proportions_ztest(count, nobs, alternative)で2群の比率差の検定を行うことができる。
- count:標本中で実際に得られた数をListで渡す
- nobs(the number of observations):標本の大きさをListで渡す
- alternative:対立仮説の設定(‘two-sided’, ‘smaller’, ‘larger’ (’smaller’: p1 < p2, larger’: p1 > p2))
返り値は(z値, p値)のタプルが返ってくる
使用する際はfrom statsmodels.stats.proportion import proportions_ztestとインポートすればいい
# import
from statsmodels.stats.proportion import proportions_ztest
# 2群の比率差の検定(例のA/Bテストを使用)
proportions_ztest([30, 33], [1000, 1000], alternative='smaller') # -> (-0.3840618481549573, 0.35046630388746547)
p値が0.05より大きいのでA<Bの有意性はない、と分かる。
■連関の検定(カイ二乗検定)
▶連関の検定とは
- 2群のカテゴリー変数間に連関があるかを検定する
- 帰無仮説には「連関が無い(独立)」、対立仮説には「連関がある(独立ではない)」を設定する
- 観測度数の分割表について検定を行う(期待度数は連関が無い場合の分割表)
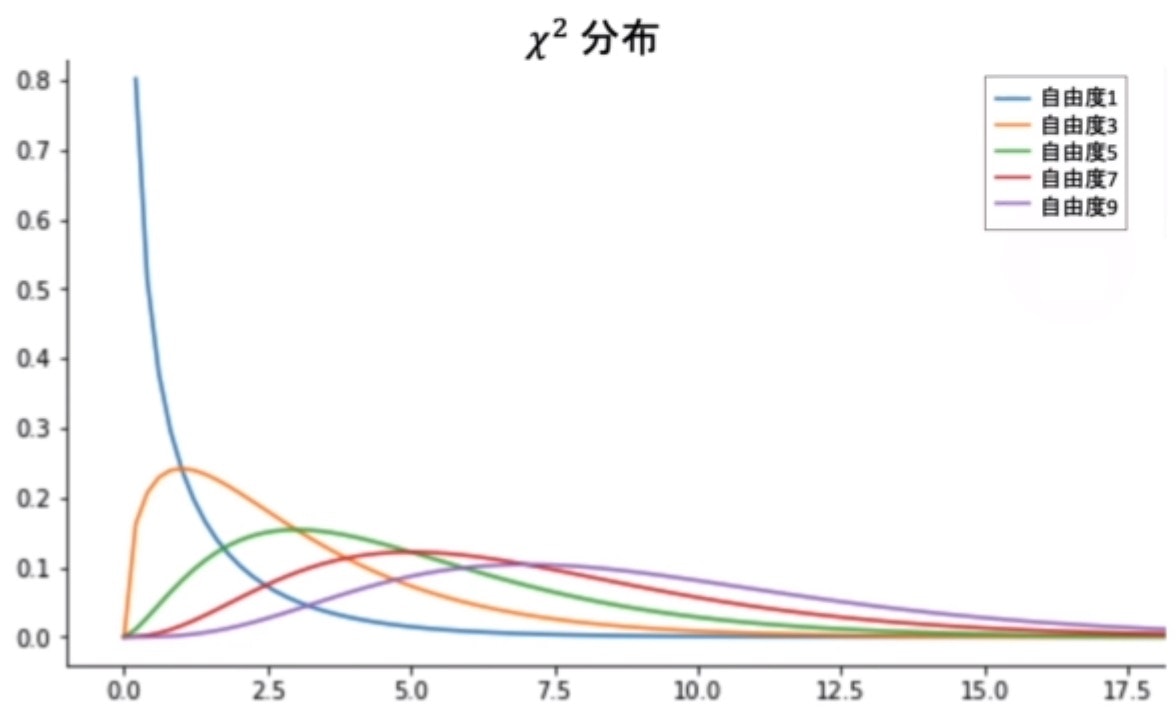
カイ二乗分布
- 帰無仮説が正しいと仮定したときに、カテゴリ変数間のカイ二乗値がどれくらいの確率で得られるかをカイ二乗分布から考える
カイ二乗値
観測度数が期待度数からどれほど離れているかを計算した値
-> (観測度数-期待度数)$^2$/期待度数の総和
詳しくはカイ二乗(chi squared)参照
- カイ二乗分布はカイ二乗値が従う確率分布で、自由度を唯一のパラメータに取る分布
「自由度=(a-1)(b-1)」(a行b列の分割表)
カイ二乗分布におけるp値
- 帰無仮説が正しいとした場合の標本から計算されたカイ二乗が得られる確率
- 2変数が独立の関係にある場合は「$χ^2=0$、$p=1$」となる
- 上手でもわかる通り「$χ^2≧0$」なので、棄却域は片側にしか存在しない
※有意水準5%は自由度1の時、「$χ^2=3.841$」
stats.chi2?contingency(obs, correction=False)で検定を行うことが可能で、obsは観測度数の分割表を渡せばいい。
correctionは「イェイツの修正」を適用するかどうかの項目で、デフォルトはTrueなので通常の連関の検定であればFalseを渡してあげればいい
返り値はchi2, p, dof, exの4つで、それぞれ「カイ二乗値、p値、自由度、期待度数」のこと
# 連関の検定(カイ二乗検定)
# 分割表作成
obs = [[15, 5] ,[15, 65]]
# chi2=カイ二乗値、p=p値、dof=自由度、ex=期待度数
chi2, p, dof, ex = stats.chi2_contingency(obs, correction=False)
▶イェイツの修正(Yates's correction)とは
- カイ二乗検定に修正を加えたもの
$χ^2=\sum_{i=1}^a\sum_{j=1}^b\frac{(n_{ij}-e_{ij})^2}{e_{ij}}$ ⇒ $χ^2=\sum_{i=1}^a\sum_{j=1}^b\frac{(|n_{ij}-e_{ij}|-0.5)^2}{e_{ij}}$ - 通常のものより、カイ二乗値が低くなる(p値が高くなる)ので棄却域に入りずらく、連関があると判定しにくくなっている
- 用途はかなり限定的で、通常は使用しなくていい
■カイ二乗検定とZ検定の関係性
- 自由度1のカイ二乗検定はZ検定と同じ
※例に使ったA/Bテストも分割表として考えると、カイ二乗検定が適用できる
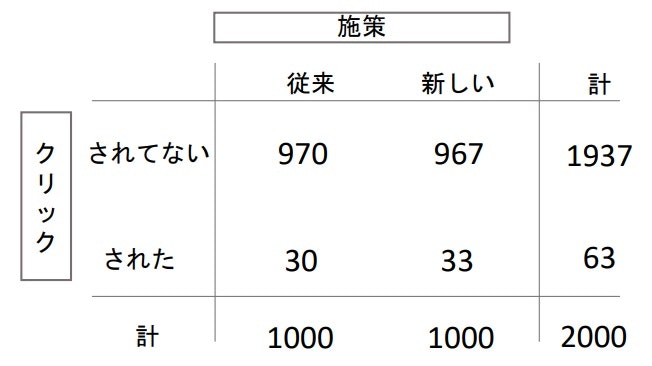
- しかし、カイ二乗検定では片側検定が行えないので、「比率の大小」の判定はできず、「比率差がある」ということしか判定できない
Challenge
Z検定と自由度1のカイ二乗検定が同じ結果になることを確認する
- データセットからカテゴリ変数の標本を2つ作成し、それぞれの標本比率の差の検定を行い、p値について確認する
- 今回は
'time'を使用
解答例
# sample準備
n = 50
sample_df1 = df.sample(n)
sample_df2 = df.sample(n)
# Z検定
count1 = sample_df1['time'].value_counts()['Dinner']
count2 = sample_df2['time'].value_counts()['Dinner']
proportions_ztest([count1, count2], [n, n], alternative='two-sided')
# -> (-2.3062266407882204, 0.021097971724778362)
# カイ二乗検定
sample1_freq = sample_df1['time'].value_counts().values
sample2_freq = sample_df2['time'].value_counts().values
stats.chi2_contingency([sample1_freq, sample2_freq], correction=False)
# -> (5.318681318681319, 0.02109797172477835, 1, array([[32.5, 17.5],[32.5, 17.5]]))
■平均値差の検定(t検定)
▶平均値差の検定とは
- 最もよく使用される検定で、t分布を使用するのでt検定といわれている
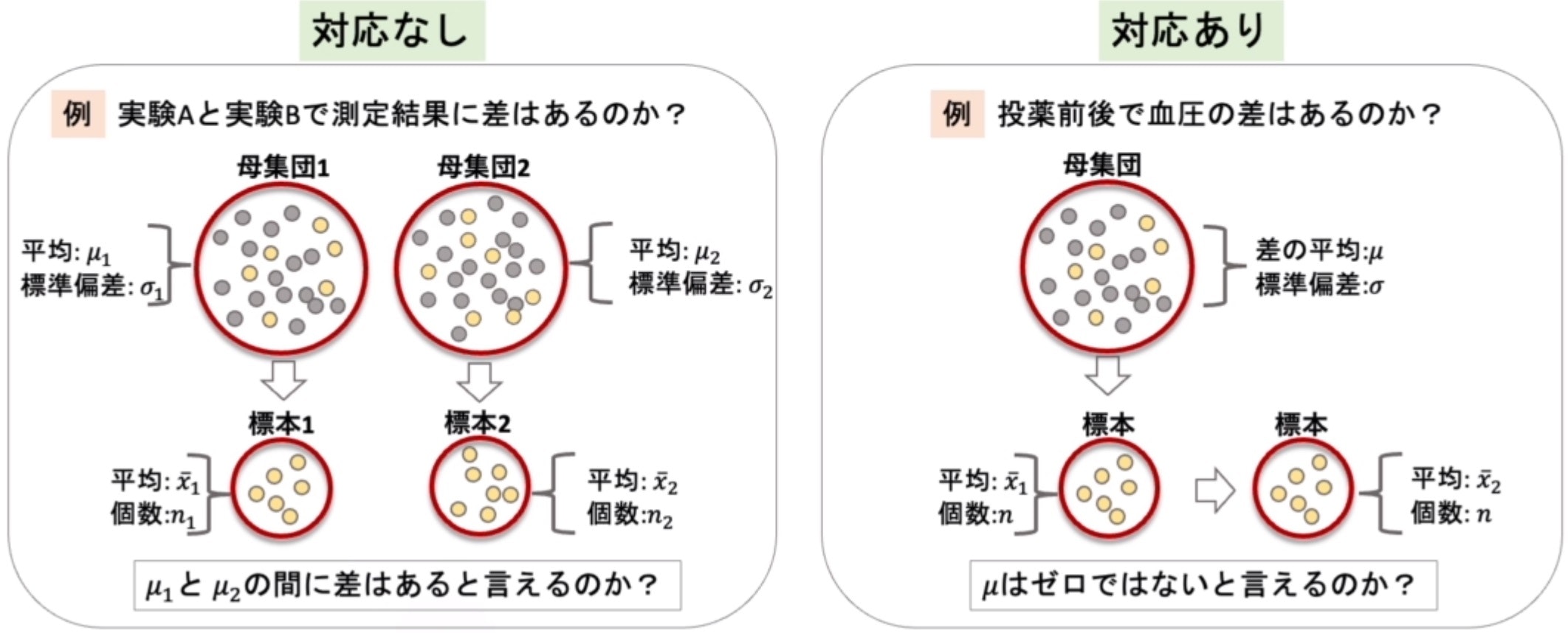
- 「対応なし」と「対応あり」の2つの方法がある
- 対応なし:それぞれ別の母集団から標本を取り、それぞれの「標本平均」に差はあるかを見る
- 対応あり:標本の施策前と施策後の「平均の差」を検定対象とする
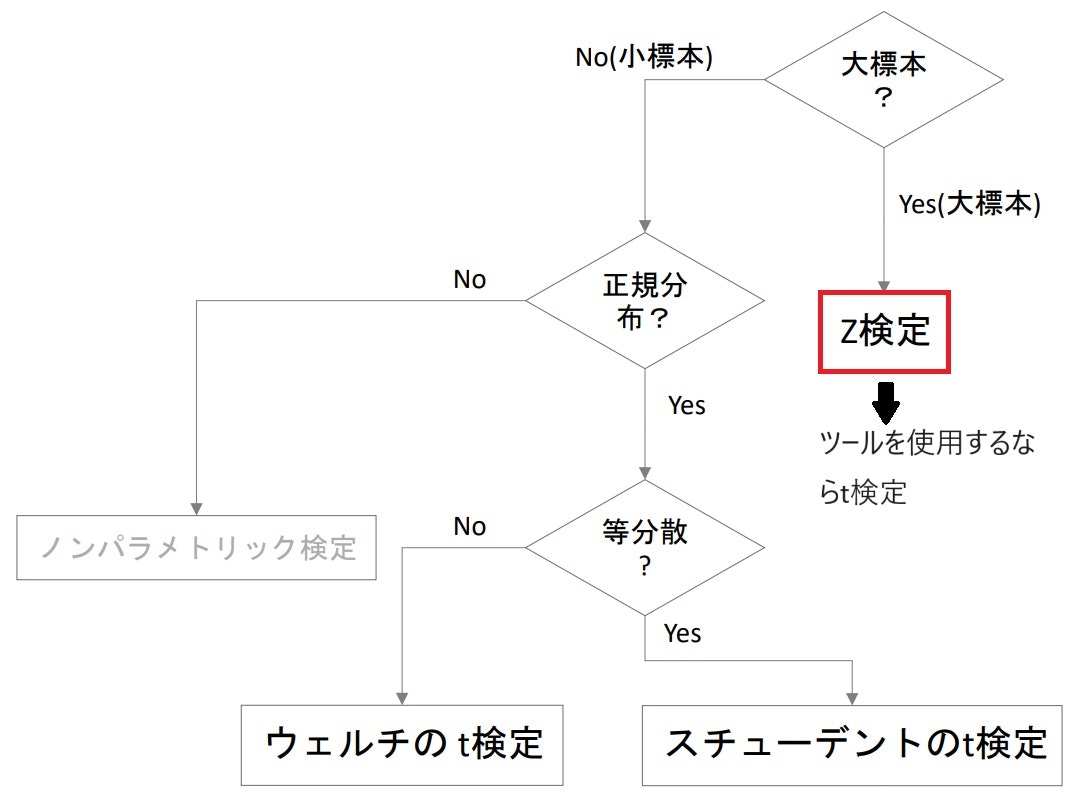
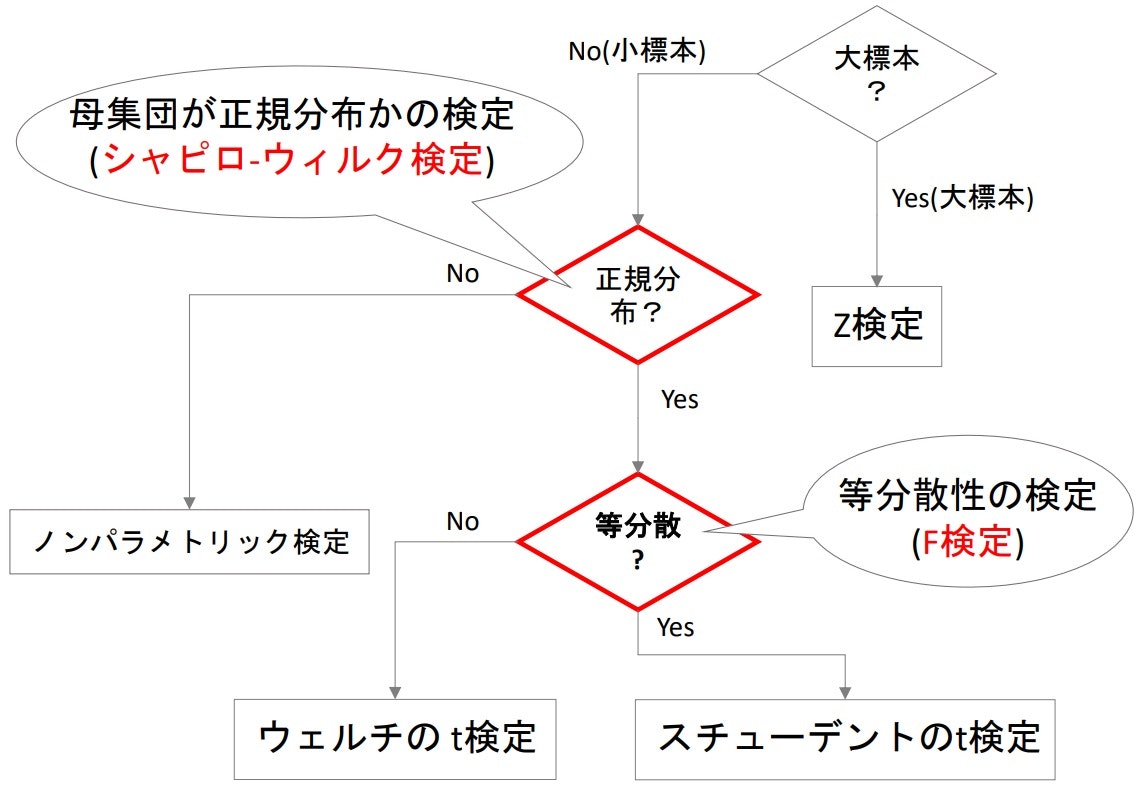
- 平均値差の検定では、大標本か小標本か、正規分布かどうか、等分散かどうかなどで使用する検定が変わってくる
- Z分布はあくまでも近似によるものなので、ツールを使用する場合はより正確なt分布を使用するt検定を行う
- 一般的に「t検定」と呼ばれるのは「スチューデントのt検定」
平均値差の標本分布
- 基本的には比率差の検定と考え方は同じで、帰無仮説(平均値差がない)が正しいとして標本分布を作成する
▶大標本の場合
- 母集団が正規分布にならなくとも中心極限定理により、標本は正規分布となる
なので、標本の平均値の差も正規分布となり、Z検定を使用することができる - 比率差の検定の時と同様に、2群の平均値差の標本分布は「平均μはそれぞれの平均の差」、「分散σ$^2$はそれぞれの不偏分散の和」の正規分布となる
※もちろん扱いやすいように「標準化」を行う($Z=\frac{\bar{x_1}-\bar{x_2}}{\sqrt{\frac{{s'}_1^2}{n_1}+\frac{{s'}_2^2}{n_2}}}$)
▶小標本の場合
スチューデントのt検定
- 母集団が正規分であり、2群の分散が等しい場合に使用できるt検定
$\bar{x}_1-\bar{x}_2$の標本分布において、分散σ$^2$($\frac{\sigma^2_1}{n_1}+\frac{\sigma^2_2}{n_2}$)を不偏分散s'$^2$($\frac{s'^2_1}{n_1}+\frac{s'^2_2}{n_2}$)で代用していたが、小標本では正規分布に近似できない
しかし、等分散(σ$^2_1$=σ$^2_2$)であれば、t分布になる。
⇒2群の母集団に共通の分散σ$^2_1$(=σ$^2_2$)の推定値が必要となる。
2群の母集団に共通な分散の推定値
- 2つの標本の全データ($n_1+n_2$)における平均からの偏差の2乗和を全体の自由度で割ったものを使用
※比率差の検定の際に推定した$\hat{p}$と似た考え方
全データ($n_1+n_2$)における平均からの偏差の2乗和
- 標本1の偏差の平方和:$\sum_{i=1}^{n^1}(x_{1i}-\bar{x_1})^2$
- 標本2の偏差の平方和:$\sum_{i=1}^{n^2}(x_{2i}-\bar{x_2})^2$
$⇒\sum_{i=1}^{n^1}(x_{1i}-\bar{x_1})^2+\sum_{i=1}^{n^2}(x_{2i}-\bar{x_2})^2⇒(n_1-1)s'^2_1+(n_2-1)s'^2_2$
全体の自由度
- 標本1 + 標本2の自由度:$(n_1-1)+(n_2-1)=n_1+n_2-2$
等分散σ$^2$の推定値:$\frac{(n_1-1)s'^2_1+(n_2-1)s'^2_2}{n_1+n_2-2}$
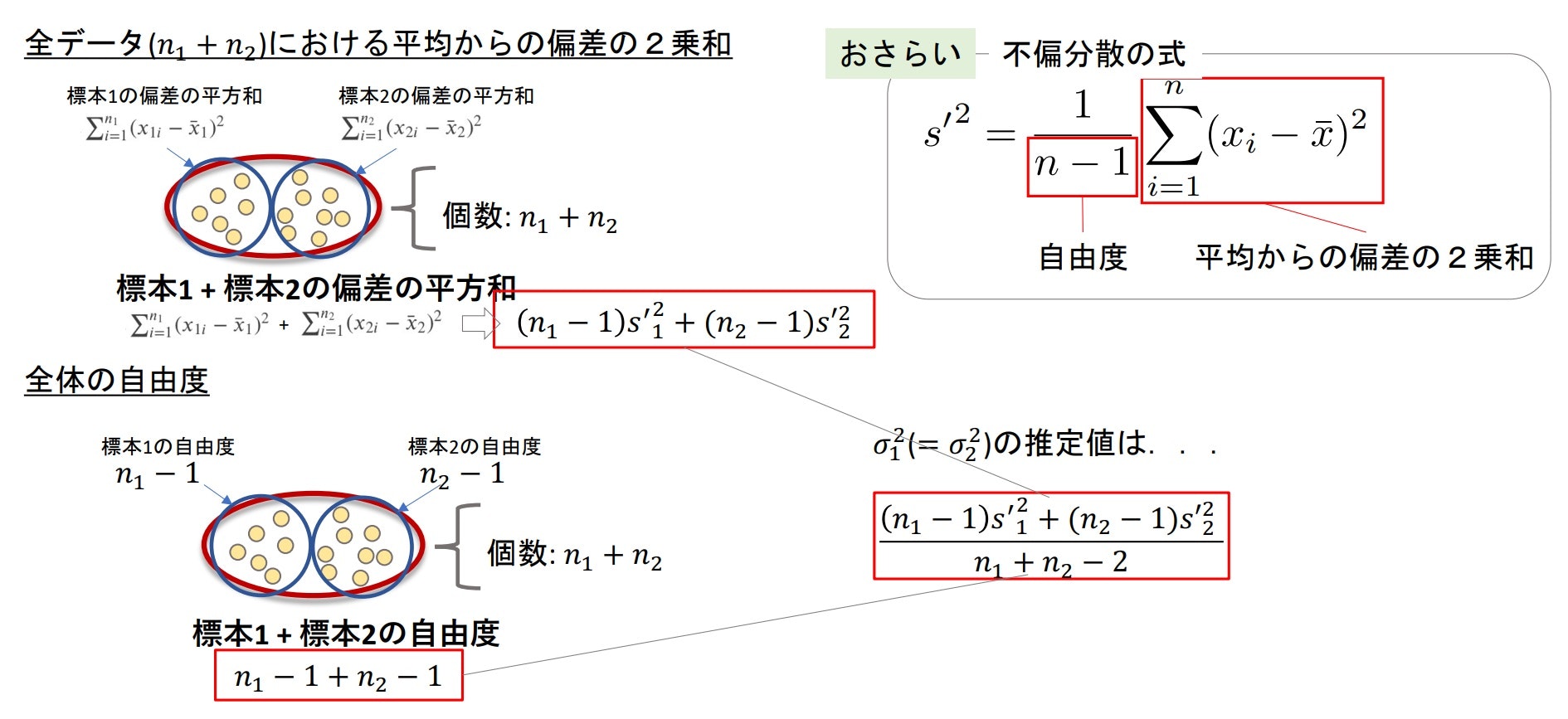
★つまり、$\bar{x}_1-\bar{x}_2$の標本分布は平均$μ=μ_1-μ_2$、分散$\sigma^2=\frac{(n_1-1)s'^2_1+(n_2-1)s'^2_2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})$の分布となる。
標準化
- もちろん扱いやすい形にするために標準化を行う(平均μを引いて、標準偏差$\hat\sigma$で割る)
$t=\frac{\bar{x_1}-\bar{x_2}-(\mu_1-\mu_2)}{\sqrt{\frac{(n_1-1)s'^2_1+(n_2-1)s'^2_2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}}=\frac{\bar{x_1}-\bar{x_2}-(\mu_1-\mu_2)}{\hat\sigma}$
※上記の式はt分布の式と同じになっている
t分布:$t=\frac{x-\mu}{\frac{s'}{\sqrt{n}}}$(ある数x、平均μ、不偏分散の平方根$\sqrt{\frac{s'^2}{n}}$)
結論
帰無仮説($\mu_1=\mu_2$)が正しいときの$t=\frac{\bar{x_1}-\bar{x_2}}{\hat\sigma}$を計算し、自由度$n_1+n_2-2$のt分布において棄却域に入るかどうかを見る。
ウェルチのt検定
- 小標本で2群の母集団の分散が等しいとは言えない場合に使用する検定($\sigma^2_1\neq\sigma^2_2$)
- 少し複雑な式になるが、$n_1$と$n_2$が大きければ標準正規分布に近似でき、Z検定となる
$t=\frac{\bar{x_1}-\bar{x_2}}{\sqrt{\frac{{s'}_1^2}{n_1}+\frac{{s'}_2^2}{n_2}}}$、t分布の自由度$\nu$(近似):$\nu\approx\frac{(\frac{{s'}_1^2}{n_1}+\frac{{s'}_2^2}{n_2})^2}{\frac{{s'}_1^4}{n_1^2(n_1-1)}+\frac{{s'}_2^4}{n_2^2(n_2-1)}}$
スチューデントのt検定とウェルチのt検定はPythonを使用すれば簡単に行うことができる。
スチューデントのt検定:stats.ttest_ind(a, b, equal_var=True)
ウェルチのt検定:stats.ttest_ind(a, b, equal_var=False)
※aとbはそれぞれの標本、返り値は(検定統計量t, p値)で返される
また、alternativeを引数に指定することで両側検定や片側検定の指定を行うことができる。
# Student's t test(両側検定:two-sided)
stats.ttest_ind(a, b, equal_var=True, alternative="two-sided")
# Welch's t test(片側検定:less, greater)
stats.ttest_ind(a, b, equal_var=False, alternative="less")
扱いやすい「ウェルチのt検定」を...!
Pythonで平均値差のt検定を行う場合は、等分散の証明が面倒なのでスチューデントのt検定ではなく、ウェルチのt検定を使用する。
Challenge
データフレーム全体を標本として、男女の平均チップ率に有意差はあるかをスチューデントのt検定とウェルチのt検定の両方で確認する
解答例
# 男女の標本作成
male_tips = df[df['sex']=='Male']['tip_rate']
female_tips = df[df['sex']=='Female']['tip_rate']
# スチューデントのt検定
stats.ttest_ind(male_tips, female_tips)
# -> Ttest_indResult(statistic=-1.0833972270477996, pvalue=0.2797103849605489)
# ウェルチのt検定
stats.ttest_ind(male_tips, female_tips, equal_var=False)
# -> Ttest_indResult(statistic=-1.1432770167349968, pvalue=0.2542456188927583)
p値がどちらも0.05より大きいので、男女の平均チップ率に有意差はないといえる。
▶正規性と等分散性の検定
平均値差の検定において、小標本の場合は2群の母集団が「正規分布」か、「等分散」か、という観点で使用する検定が異なるとなっていた。
正規分布と等分散についての検定も存在し、それぞれ正規性の検定、等分散性の検定と呼ばれる。
ただ、検定の前に検定を行うのは不適切ではないのか、という意見も存在する。
それぞれの検定において有意水準5%で検定を行った場合、「それぞれで5%の確率で間違った検定を行ってしまう」ということが言える。
つまり、全体で見ると有意水準5%を担保できていないことになるため。
正規性の検定(シャピロ-ウィルク検定)
- 検定の多くは「正規分布に従う」と仮定して行われており、正規分布からの標本なのかどうかの検定は重要度が高い
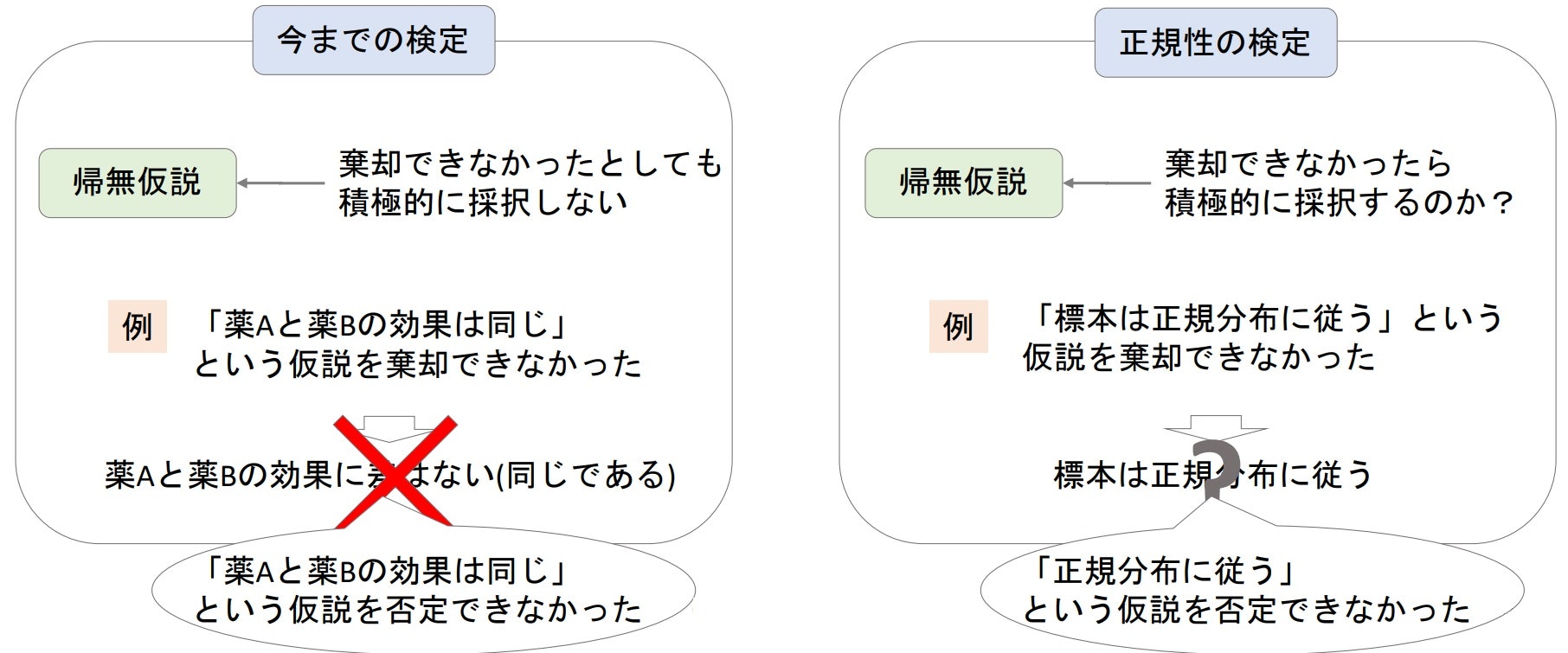
- 今までのように帰無仮説を棄却する前提で行う検定と異なり、帰無仮説が棄却されないことを期待する検定となる
- 帰無仮説:母集団が正規分布に従う -> 観測分布と正規分布に"差がない"(※棄却することを狙っていない)
- 対立仮説:母集団が正規分布に従わない(※成立することを狙っていない)
「帰無仮説が棄却される=差がない」ではない!
今までの検定でも帰無仮説が棄却されなかったことはあったが、この場合はあくまで「差がないという仮定を"否定できない"」ということであって、「差がない」と断定できるものではないことに注意。
- シャピロ-ウィルク検定においても、帰無仮説が棄却されなかった場合は「母集団は正規分布だという仮定を否定できない」程度の解釈にとどめておく
※ただ、正規性を証明するには十分なので、固執する必要はない
- シャピロ-ウィルク検定はQ-Qプロットにおいて、どれほど直線からずれているかヲ検定する
この時の検定統計量は標本の順序統計量と正規分布の順序統計量の期待値の相関(厳密には相関とは違い、相関のようなもの)
Q-Qプロット(Quantile-Quantile plot)
- 得られたデータが理論上の分布(例えば正規分布)にどれほど近いかと視覚的に確認できるプロット
- 観測データを小さい順に並び変え、その値をy軸に、値yの時の累積分布関数(CDF)をx軸に取ったプロット
- このプロットが直線上にあればあるほど観測データは理論分布に近いということが言える
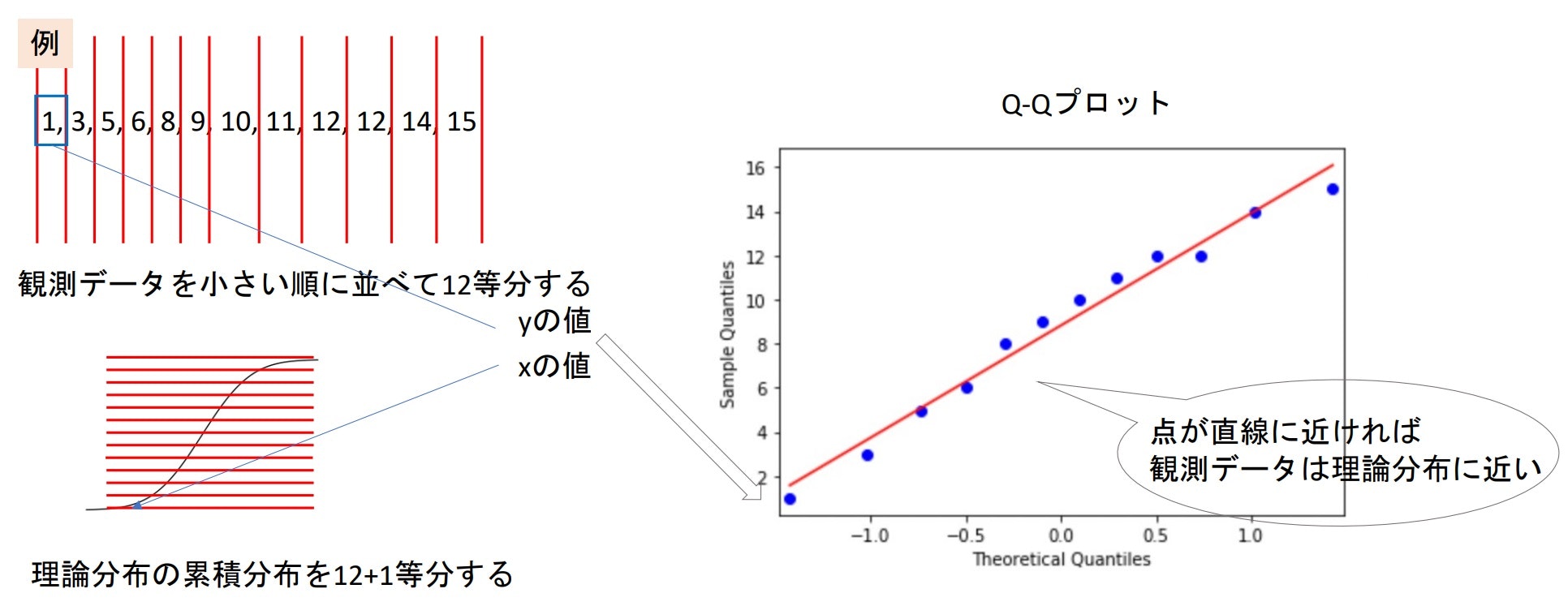
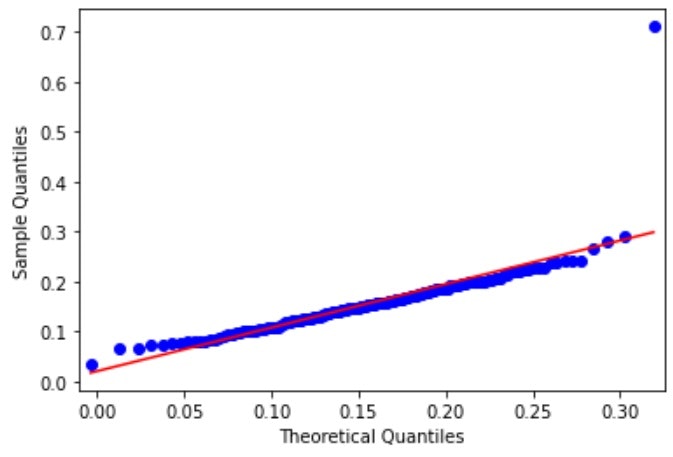
標準正規分布のQ-Qプロットの例
※標準正規分布からランダムに200件抽出した際のQ-Qプロット
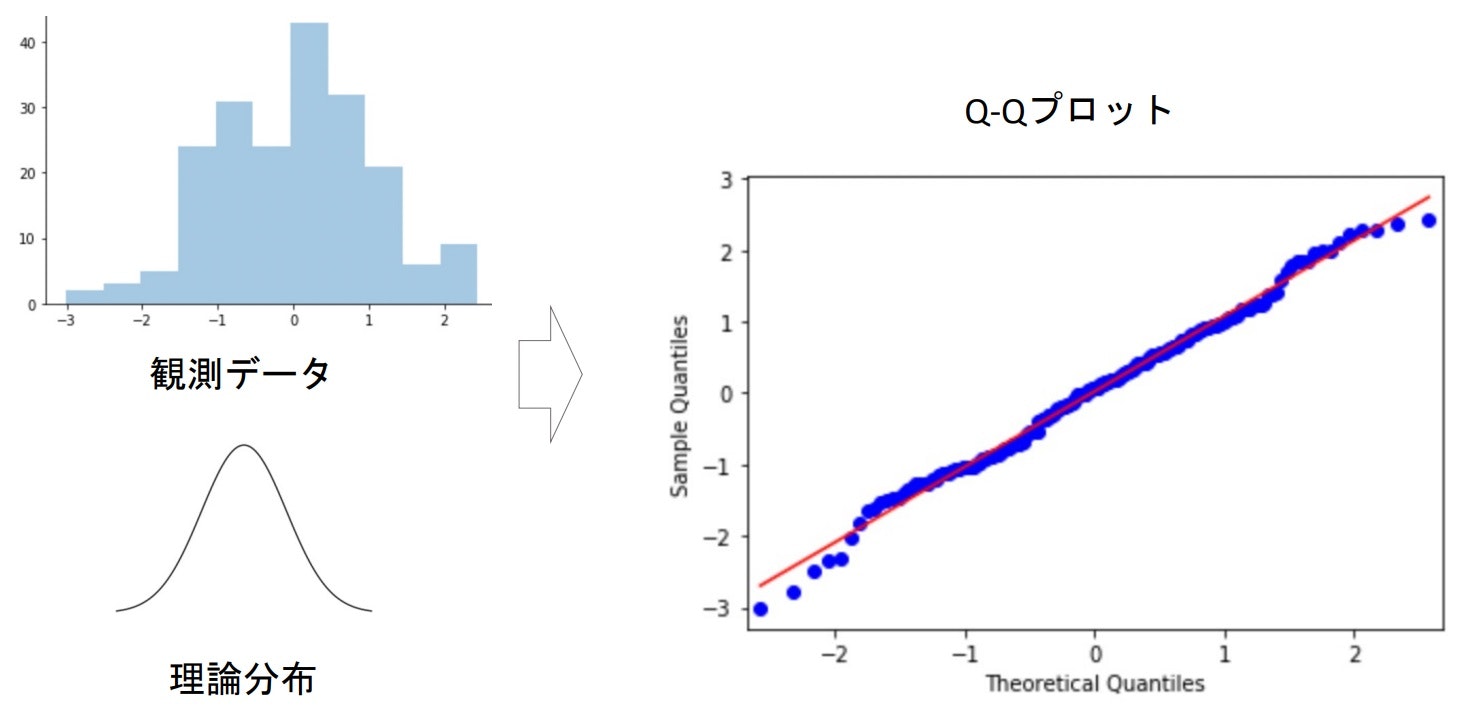
statsmodels.api.qqplot(data, line='r')で簡単にdataに対するQ-Qプロットを描画できる。
返り値はmatplotlibのfigureで、引数line='r'はregression(回帰)の結果を描画してくれる。
また、引数にdist=figで好きな理論分布(fig)を指定することで、その分布と観測データを比較するようにできる。
# Q-Qプロット(男女のtip_rate)
male_tipr = df[df['sex']=='Male']['tip_rate']
female_tipr = df[df['sex']=='Female']['tip_rate']
# 男性のtipのQQプロット
fig = qqplot(male_tipr,
line='r',
dist=stats.norm(loc=np.mean(male_tipr),
scale=np.sqrt(stats.tvar(male_tipr))))
# 女性のtipのQQプロット
fig = qqplot(female_tipr,
line='r',
dist=stats.norm(loc=np.mean(female_tipr),
scale=np.sqrt(stats.tvar(female_tipr))))
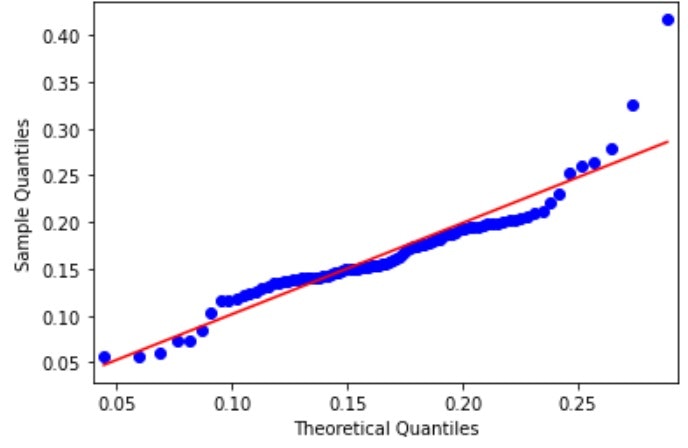
女性のチップ率のほうは男性のものよりも正規分布から遠いデータとなっていることが視覚的、直感的に判断することができる。
stats.shapiro(x)でデータxに正規性があるか確認することができる。
戻り値は(検定統計量, p値)となる。
# シャピロ-ウィルク検定(男女のtip_rate)
# 男性
stats.shapiro(male_tipr)
# -> ShapiroResult(statistic=0.7447847127914429, pvalue=3.2243281107541917e-15)
# 女性
stats.shapiro(female_tipr)
# -> ShapiroResult(statistic=0.8982974290847778, pvalue=4.717996489489451e-06)
どちらもp値がかなり小さいものになっており、帰無仮説が棄却されてしまっている。
上のQ-Qプロットでは直線状のデータが集まっているように見えるが、外れ値が1つ、ないし2つ存在するだけでp値はかなり小さくなってしまう。
# 外れ値を除く
# 男性
stats.shapiro(np.sort(male_tipr)[:-1])
# -> ShapiroResult(statistic=0.9931070804595947, pvalue=0.6644759774208069)
# 女性
stats.shapiro(np.sort(female_tipr)[:-2])
# -> ShapiroResult(statistic=0.9696651697158813, pvalue=0.04252713546156883)
外れ値を除いたとしても、女性のほうについては正規分布からのデータとは言えないという検定結果となった。
シャピロ-ウィルク検定とQ-Qプロットは併用する
シャピロ-ウィルク検定を行う際にQ-Qプロットも同時に使用することで、外れ値の確認やデータがどれほど直線状に存在するかが視覚的に確認できるので、検定の納得感を上昇させることができる。
等分散性の検定(F検定)
- 母集団が正規分布であることが前提となる検定
- 2群の標本の分散(不偏分散s'$^2$)の比率を検定に使用
$F=\frac{{s'}_1^2}{{s'}_2^2}$ (通常大きい方を分子に置くので、比率は1以上となる) - 分散の比率の標本分布をF分布と呼ぶ
- 帰無仮説には「分散に差がない」、対立仮説に「分散に差がある」を設定する
F分布
- χ$^2$を使って表すことができる
χ$^2$の定義:$(観測度数-期待度数)^2/期待度数の総和$
-> もう一つの定義:$偏差の平方和/分散$
$χ^2=\sum_{i=1}^n\frac{(x_1-\bar{x})^2}{\sigma^2}=\frac{(n-1)s'^2}{\sigma^2}$ ※$s'^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2$より
よって、帰無仮説が正しい($\sigma_1^2=\sigma_2^2$)とするとき
$F=\frac{{s'}_1^2}{{s'}_2^2}=\frac{\frac{1}{n_1-1}\chi_1^2}{\frac{1}{n_2-1}\chi_2^2}$
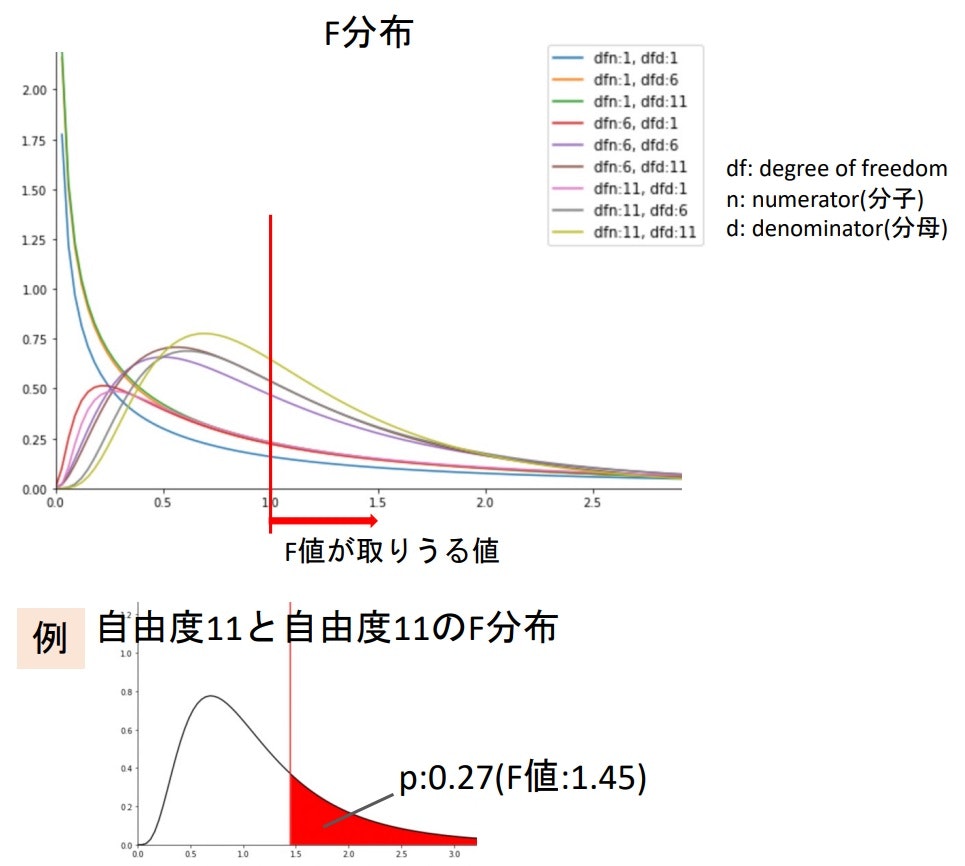
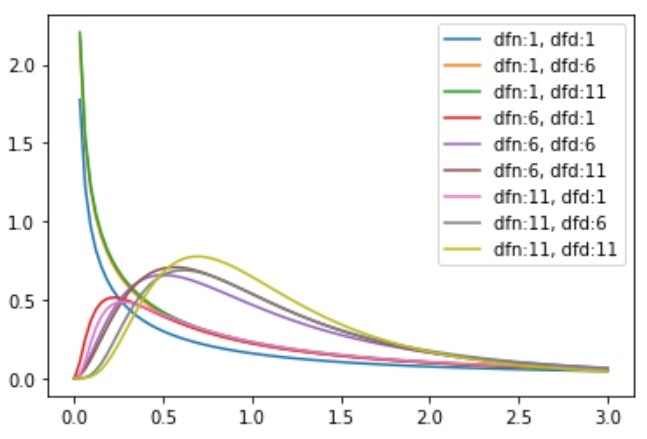
stats.f(dfn, dfd)でF分布についての値を扱うことができる。
dfn, dfdはそれぞれ、分子の自由度と分母の自由度を指定する。
stats.f(dfn, dfd).pdf(x)で値xの時のF分布における値を取得可能。
# いろんな自由度のF分布の描画
x = np.linspace(0, 3, 100)
for dfn in range(1, 12, 5):
for dfd in range(1, 12, 5):
y = stats.f.pdf(x, dfn=dfn, dfd=dfd)
plt.plot(x, y, label=f'dfn:{dfn}, dfd:{dfd}')
plt.legend()
Challenge
データセットを標本として、男女のチップ率(tip_rate)の分散に差があるかをF分布を使って検定する。
解答例
# 男女のチップ率
male_tipr = df[df['sex']=='Male']['tip_rate']
female_tipr = df[df['sex']=='Female']['tip_rate']
# F値計算
n1 = len(male_tipr)
n2 = len(female_tipr)
dfn = n1 - 1
dfd = n2 - 1
var1 = stats.tvar(male_tipr)
var2 = stats.tvar(female_tipr)
f = var1/var2 # -> 1.4588472200534603
# p値計算
stats.f(dfn=dfn, dfd=dfd).sf(f) # -> 0.027100863454374447
※p値が0.05より小さいので、帰無仮説は棄却され、等分散とは言えないと分かる。
▶対応ありの平均値差の検定(t検定)
- 対応なしの時と違い、対応ありでは同じ母集団から標本を作製する
- 何か施策を「行う前」と「行った後」で差はあるかを検定する
変化量
- 標本における個々の対応前後の「差(変化量d)」の平均$\bar{d}$について考える
変化量の平均の標本分布
- 変化量の標本平均は平均$\mu_d$、分散$\frac{\sigma_d^2}{n}$の正規分布となる
($\mu_d$は変化量の母集団の平均、$\sigma_d^2$は分散) - もちろん、扱いやすくするために標準化を行う
母標準偏差$\sigma_d$は未知なので、不偏分散の平方根$s'_d$を推定量として使用し、t分布について考える
$t=\frac{\bar{d}-\mu_d}{\frac{s'_d}{\sqrt{n}}}$
対応ありのt検定
- 帰無仮説を「平均値差に差がない($\mu_d=0$)」として、検定統計量tが自由度n-1のt分布において棄却域に入るかどうかを考える
$t=\frac{\bar{d}}{\frac{s'_d}{\sqrt{n}}}$ ($\mu_d=0$より)
stats.ttest_rel(a, b)で対応ありのt検定を行うことが可能で、戻り値は(検定統計量t, p値)となる。
aとbはデータarrayで、それぞれ対応するデータが同じ項番に格納されている必要がある。
下記データを使用して、実際の動作を確認すると、
https://github.com/Opensourcefordatascience/Data-sets/blob/master/blood_pressure.csv
(実際の血液データ:血圧を下げる薬を投薬)

# データ読み込み
bp_df = pd.read_csv('data/blood_pressure.csv')
# 血圧が下がったか見たいので、片側検定
stats.ttest_rel(bp_df['bp_before'], bp_df['bp_after'], alternative='greater')
# -> Ttest_relResult(statistic=3.3371870510833657, pvalue=0.0005648957322420411)
# それぞれのbeforeとafterの差(変化量)の平均を確認してみる
bp_df['delta'] = bp_df['bp_before'] - bp_df['bp_after']
bp_df['delta'].mean() # -> 5.091666666666667
# 変化量の分布
sns.boxplot(x=bp_df['delta'])
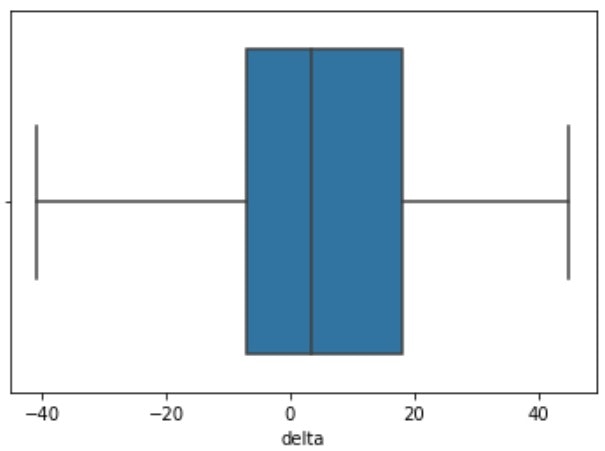
t検定において「p値 < 0.05」なので帰無仮説が棄却され、変化量の平均値差に差がないとは言えない、ということが分かった。
また、変化量の平均やboxplotを見ても、「before - after > 0」となっているので、「血圧を下げる」効果はあるといえる。
■検定の誤りと検定力
▶検定の誤りと検定力とは
- 検定の誤りとはその名の通り、事実と異なる結果(帰無仮説が正しいのに対立仮説を採択、またはその逆)を出してしまうこと
- 検定とは通常、対立仮説を採択することを目指している
- どれだけ正しい検定を行うことができるかを表すのが検定力
▶第1種の誤りと第2種の誤り
- 第1種の誤り:帰無仮説が正しいのに、棄却してしまった(対立仮説を採択した)
- 第2種の誤り:帰無仮説を棄却すべき(対立仮説が正しい)なのに、帰無仮説を採択した
※p<0.05での誤りが第1種、p>=0.05での誤りが第2種
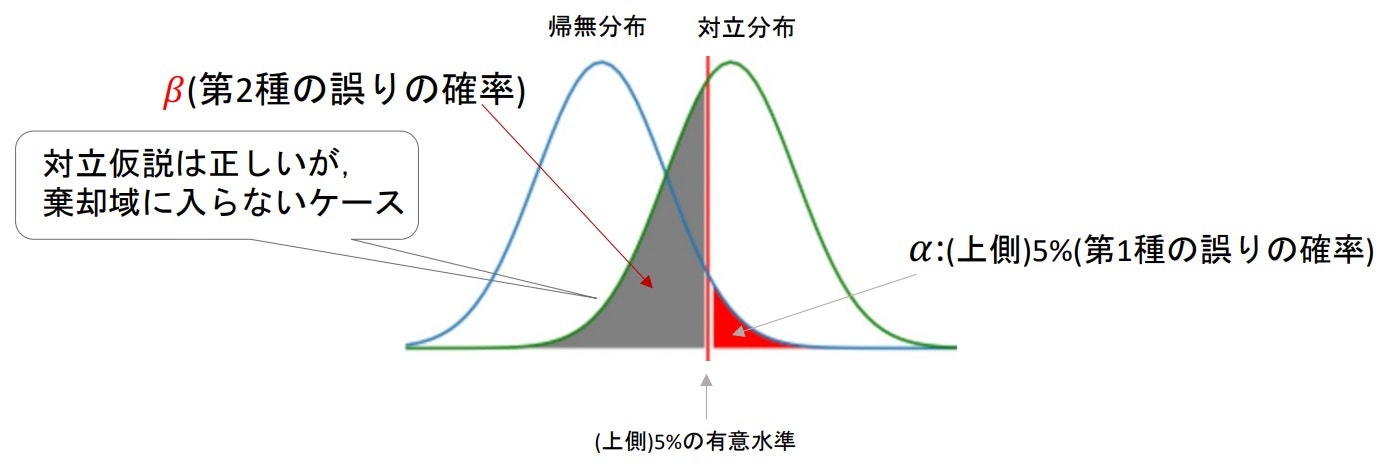
第1種の誤りを起こす確率α
- 有意水準と同じ(有意水準5%なら、$\alpha$も5%)
※「慌($\alpha$)てて棄却する$\alpha$」という覚え方がある
第2種の誤りを起こす確率β
- 帰無仮説が正しいとしたときの標本分布(帰無分布)と対立仮説が正しいとしたときの標本分布(対立分布)について考える必要がある
※$\beta$の時は対立仮説が正しいので、対立分布は実際の分布ということになる - 帰無分布と対立分布を重ねて、帰無分布の棄却域を基準にしたときの対立分布のCDFが確率$\beta$となる
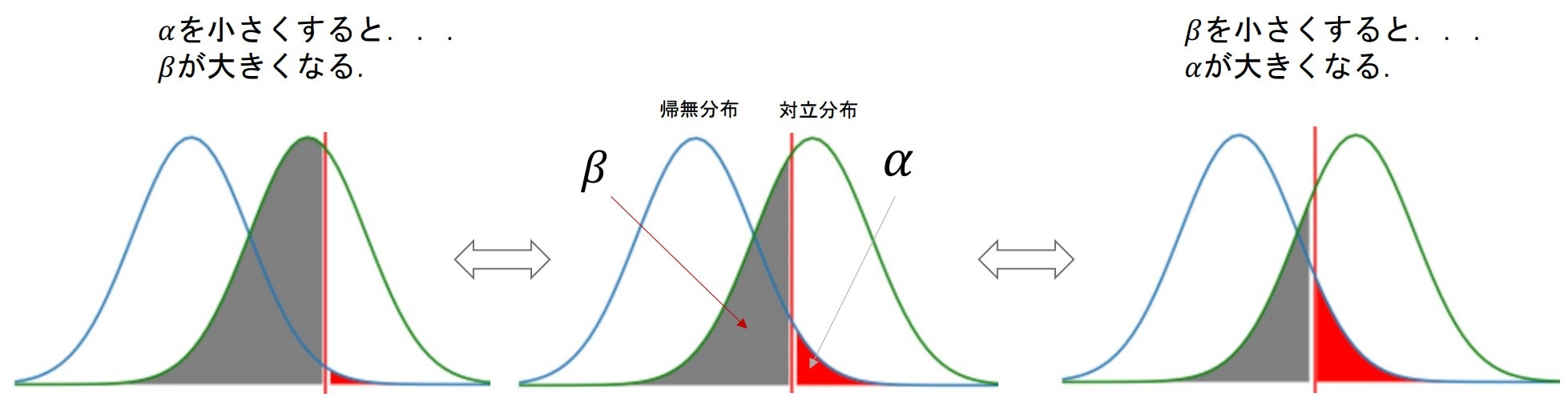
αとβのトレードオフ
- 検定の際の誤りはなるべく下げたいが、$\alpha$と$\beta$はトレードオフの関係にあり、同時に下げることができない
▶検定力(power)
- どれだけ正確に帰無仮説を棄却し、対立仮説を採択できるか
⇒ 対立仮説が正しいという前提で「どれだけ正しく対立仮説を成立できるか」が重要 - 間違って帰無仮説を採択した場合は「第2種の誤り($\beta$)」なので、検定力は「$1-\beta$」となる
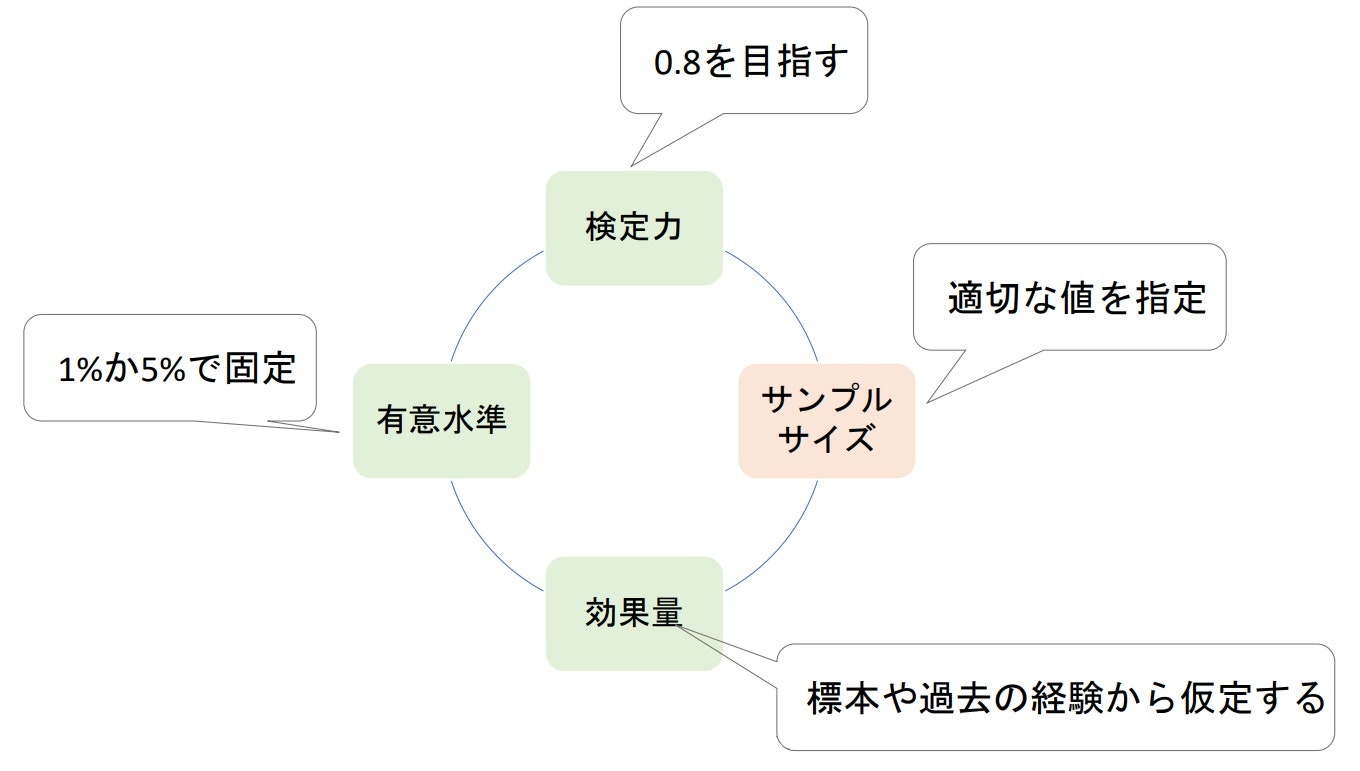
⇒検定力は高ければいいわけではなく、うまく操作する必要がある - 検定力に影響を与える3つの要素
- 有意水準
- サンプルサイズ
- 帰無分布と対立分布の差(効果量)
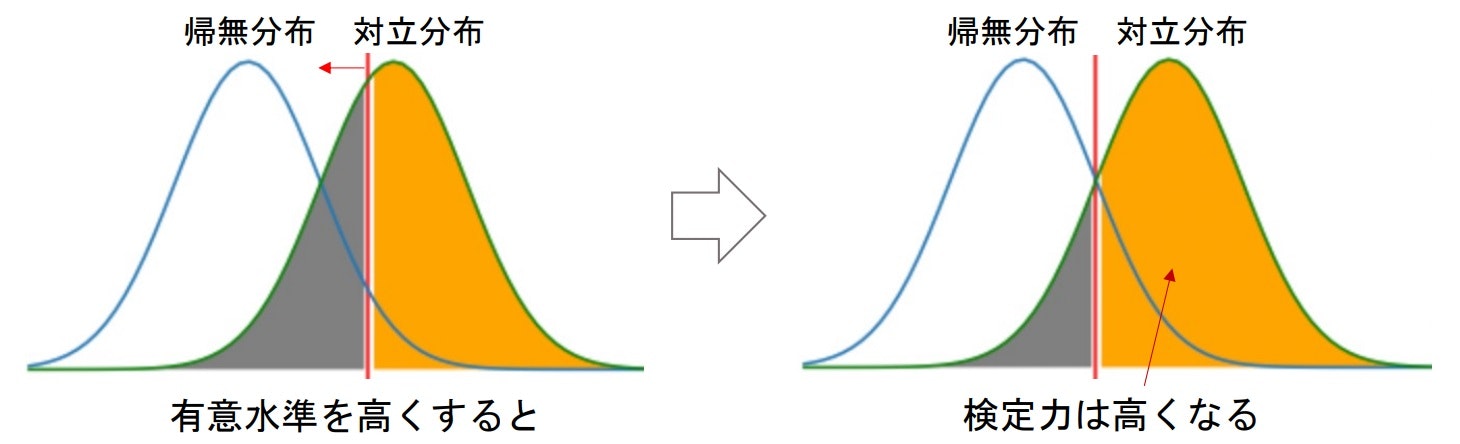
検定力と有意水準
- 有意水準を高くすると棄却域が大きくなるので、帰無仮説を棄却しやすくなる
⇒ 対立仮説が成立しやすい ⇒ 検定力が高くなる
※しかし有意水準を高くするのが適切ではないのは感覚的にもわかると思う。
※特に理由がなければ、5%か1%にする。
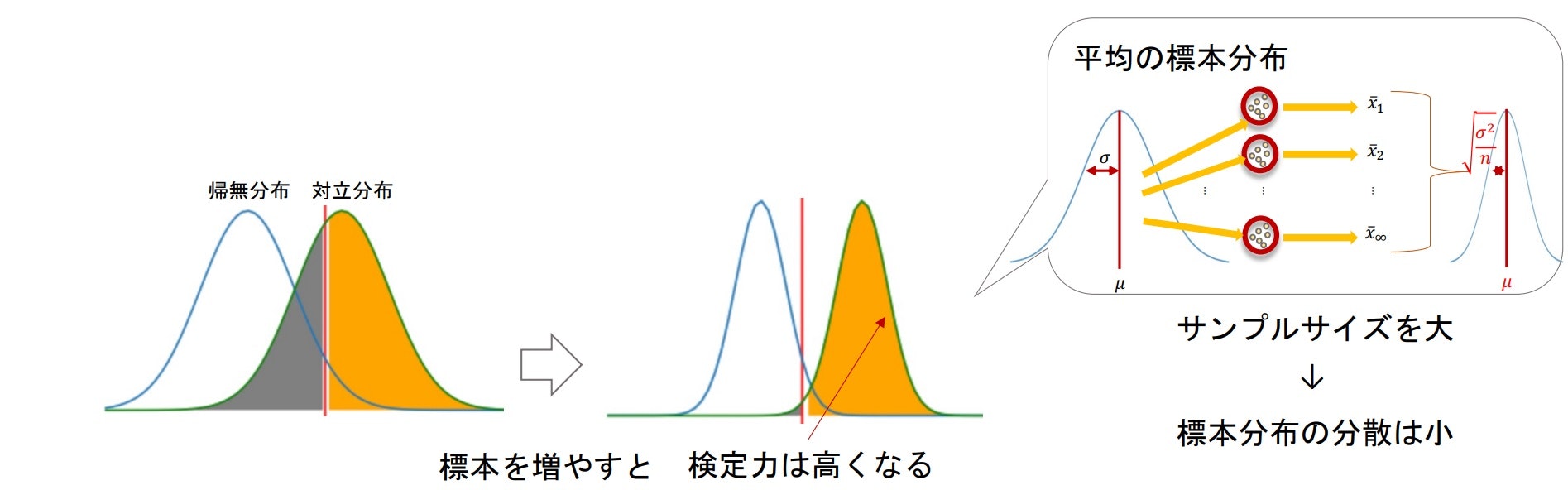
検定力とサンプルサイズ
- 唯一自分で操作できる要素
- サンプルサイズが大きくなれば、標本分布はとんがっていくはず(分散$\frac{\sigma^2}{n}$より)
⇒ そのため、帰無分布と対立分布が重なっている部分が小さくなり、検定力($1-\beta$)は大きくなる
サンプルサイズが大きければいい、というわけではない
サンプルサイズが大きい場合、「微小な差」でも「有意差あり」とでてしまう。
ほんのちょっとの効果(誤差かもしれない)しかないのに有意差ありと出てしまうのは、現実的に意味がない。
⇒ 検定の弱点(有意差の有無だけで、差の程度を見ていない)
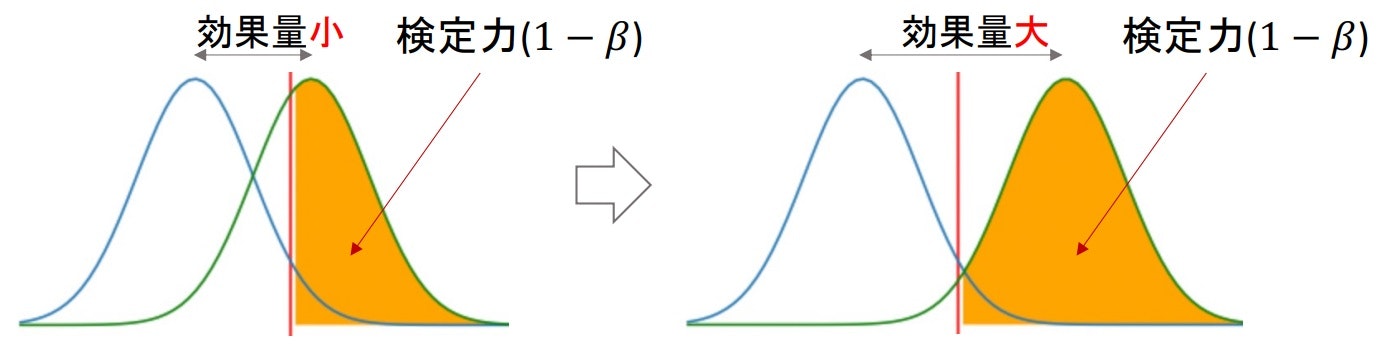
検定力と効果量
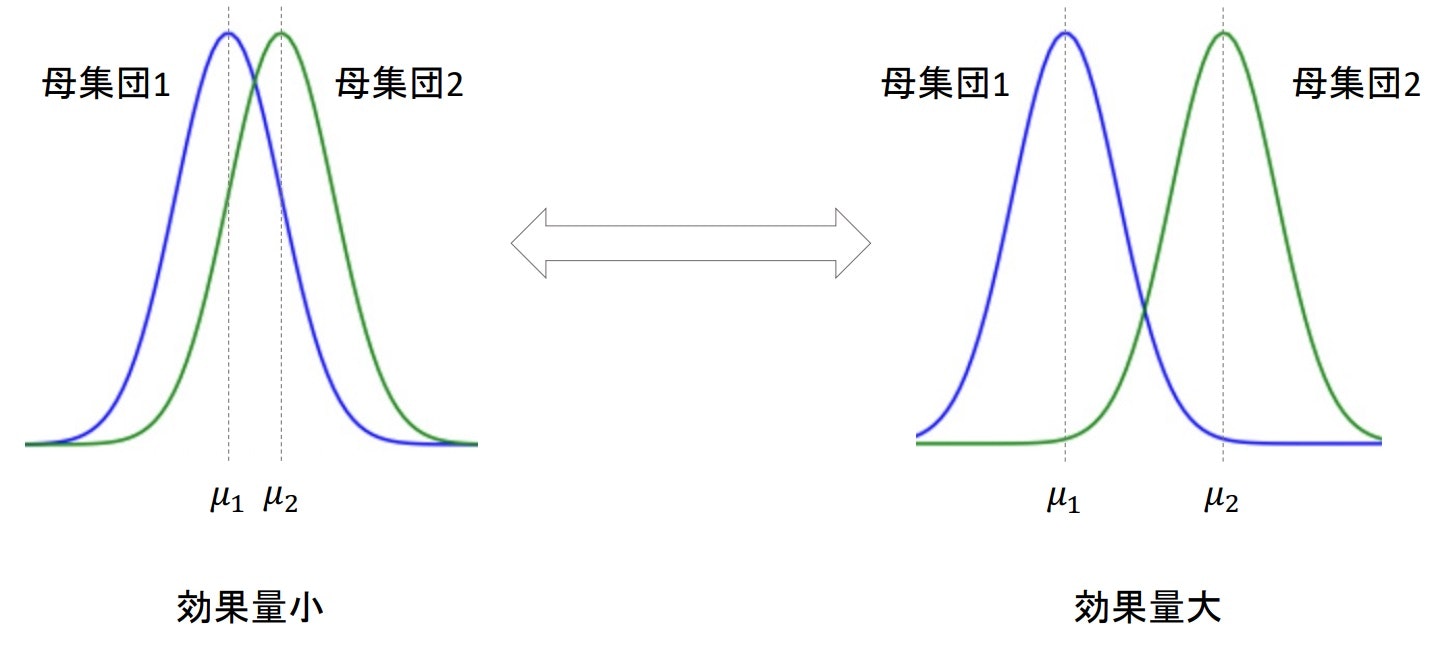
- 帰無分布と対立分布がどれほど離れているかを表したのが「効果量」
⇒ 施策Aと施策Bとの間に大きな差があった(効果的だった) ⇒ 効果量 - 効果量が大きい(帰無分布と対立分布が離れている)ほど棄却域に入りやすくなる
「検定力、有意水準、サンプルサイズ、効果量」の4つのバランスを考える必要がある。
1つの目安として検定力が0.8になるようにサンプルサイズを決定するようにする(Jacob Cohen提唱)
■検定力分析(power analysis)
▶検定力分析とは
- 有意水準、効果量、サンプルサイズ、検定力を求めること
特に適切なサンプルサイズを算出するのが目的となる。 - 検定力分析を行う際に、すでに手元に標本があるかどうかで対応が変わってくる
- これからサンプル(標本)を抽出する場合は、想定する検定量(目指すべきは0.8)に基づいてサンプルサイズを算出する。
- すでにサンプルがある場合は、p値と一緒に効果量も報告する。
p値と効果量
前項にも記載があるが、サンプルサイズが大きければ微小な差異でも有意差ありと出てしまう。なので、同じ母集団から抽出したとしてもサンプルサイズの大小で有意差のあるなしが変化してしまう場合がある。
そのため、p値だけでなく効果量も評価対象にすることで、効果的な検定だったのかを判断する。
例えば、「有意差あり」という結果が出たが、効果量が小さければ「本当に差があるの?」、と疑問を持つことができる。
※検定ごとに異なる検定力分析が存在するが、今回は「対応なしの2群の平均値差の検定」を例にする。
▶効果量(effect size)
- 検定で明らかにしたい差の量
- 単純に「A-B」で求まるものではなく、標準化する必要がある
※評価対象によっては差のレンジが異なるから(チップとチップ率など) - 効果量を「標準偏差いくつ分離れているか」で測る
$\frac{母集団1の平均-母集団2の平均}{母集団1と母集団2を合わせた標準偏差}=\frac{\mu_1-\mu_2}{\sigma}$
もちろん母集団の平均や標準偏差はわからないので、標本の平均や不偏分散の平方根を使用する。
※2群を合わせた不偏分散については2群の母集団に共通な分散の推定値を参照
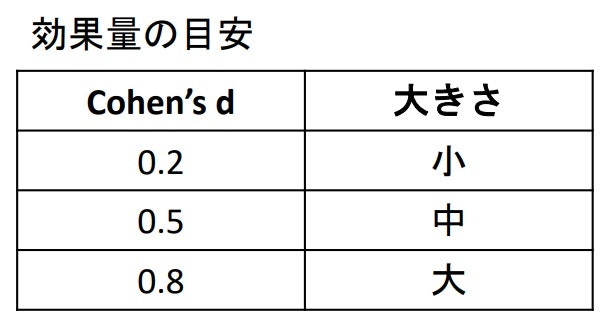
▶Cohen's d
- すでに標本がある際、効果量の算出したい場合に使用する
- 標本から計算する標準化された効果量の指標の1つ
※1を超えることもあるので注意
$\frac{\hat{x_1}-\hat{x_2}}{\hat\sigma}$ - 実際には絶対値を取ることが多い
厳密には…
今回はCohen's dを扱っているが、厳密には不偏分散を使用する場合はHedge's gやCohen's gと呼ばれる。
しかし、昨今のツールではCohen's dの算出においても不偏分散が使用されることが多く、あまり区別されていない様子。
Challenge
- Cohen’s dを算出する関数を作成する
def cohen_d(x, y) - tipデータを標本として男女のチップ率の効果量を求める
1の解答例
def cohen_d(x1, x2):
n1 = len(x1)
n2 = len(x2)
dof = n1 + n2 - 2
std = np.sqrt(((n1-1)*stats.tvar(x1) + (n2-1)*stats.tvar(x2))/dof)
# np.abs()は絶対値を算出する
return np.abs((np.mean(x1) - np.mean(x2)))/std
2の解答例
male_tip_rate = df[df['sex']=='Male']['tip_rate']
female_tip_rate = df[df['sex']=='Female']['tip_rate']
cohen_d(male_tip_rate, female_tip_rate) # -> 0.14480153987269248
-> 男女のチップ率の効果量は低いことがわかる
▶Pythonで検定力分析
-
statsmodels.stats.power.TTestIndPowerクラスの.solve_power()で算出することが可能
※power = TTestIndPower()でインスタンス化
※※あくまで2群の平均値差の検定の検定力についての関数 - 有意水準、効果量、検定力、サンプルサイズを他の値から算出する
-
.solve_power(effect_size, nobs1, alpha, power, ratio, alternative)と引数を与えることが可能で、算出したいパラメータをNoneにする
- effect_size:効果量(Cohen's d)
- nobs1:標準1のサイズ
- alpha:有意水準
- power:検定力
- ratio:標本1に対する標本2の大きさ(比率:$\frac{n_2}{n_1}$)
- alternative:'two-sided'、'smaller'、'larger'
Challenge
- tipデータを標本として男女のチップ率の平均値差の検定の検定力を求める
(両側検定で有意水準5%) - 上記と同じ条件の時、検定力を0.8にするのに必要なサンプルサイズを算出する
1の解答例
# インスタンス生成
power = TTestIndPower()
male_tip_rate = df[df['sex']=='Male']['tip_rate']
female_tip_rate = df[df['sex']=='Female']['tip_rate']
# t検定の結果
stats.ttest_ind(male_tip_rate, female_tip_rate, equal_var=False)
# -> Ttest_indResult(statistic=-1.1432770167349968, pvalue=0.2542456188927583)
effect_size = cohen_d(male_tip_rate, female_tip_rate)
n1 = len(male_tip_rate)
n2 = len(female_tip_rate)
# 検定力を求める
stats_power = power.solve_power(effect_size=effect_size, nobs1=n1, alpha=0.05, power=None, ratio=n2/n1) # -> 0.19038260700802212
2の解答例
# 効果量を0.2とした時の検定力0.8に必要な標本1のサイズを求める
power.solve_power(effect_size=0.2, nobs1=None, alpha=0.05, power=0.8, ratio=1)
# -> 393.4056989990335
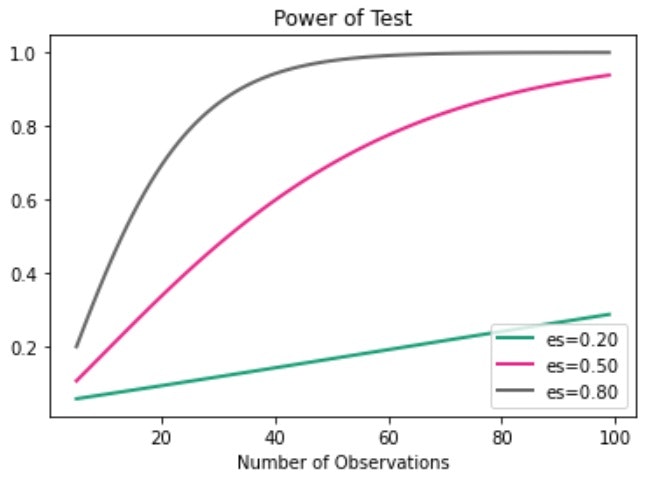
▶検定力の推移を描画
- それぞれの効果量において、サンプルサイズの変化に応じて検定力がどのように推移するかを描画することが可能
-
statsmodel.stats.power.TTestIndPower()クラスの.plot_power()を使用 -
.plot_power(dep_var, nobs, effect_size, alpha)と引数を指定する
- dep_var:x軸の変数、どの値についての検定力の推移を表示したいか(例 'nobs'、'effect_size', 'alpha')
- nobs:標本のサイズ(x軸に指定した場合は、x軸のarray)
- effect_size:効果量のリスト
- alpha:有意水準
# サンプルサイズの変化に応じた検定力の推移を描画
fig = power.plot_power(dep_var='nobs', nobs=np.array(range(5, 100)), effect_size=[0.2, 0.5, 0.8], alpha=0.05)