背景
ベテラン技術者の直観をAIで再現できないか?
私はメーカーに勤めて5年の若手技術者なのですが,モノづくりはベテラン技術者の「カン,コツ,そして度胸」に頼っている部分が結構あるなぁと思っています.AIにシミュレーション結果を学習させることで,ベテラン技術者の直観を再現できないか?と考えました.そこで,まずは簡単なプレス成形シミュレーション(角筒絞り加工解析)で試してみました.
プレス成形シミュレーション
角筒プレス加工シミュレーション
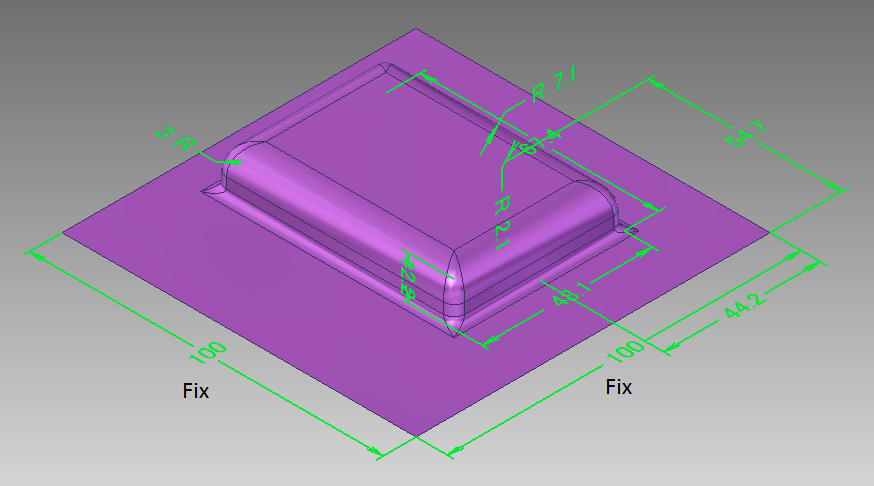
角筒絞りとは板からつなぎ目のない角筒容器を作るプレス加工方法です.図1に角筒絞り加工解析結果の例を示します.角筒容器が深く,小さい程,材料が大きく伸ばされて,板厚が減少します.シミュレーションは有限要素法を用いました.材料は鉄です.今回は最初なので,計算を軽くするために1ステップ法という金型をモデル化しない解析手法を用いました.
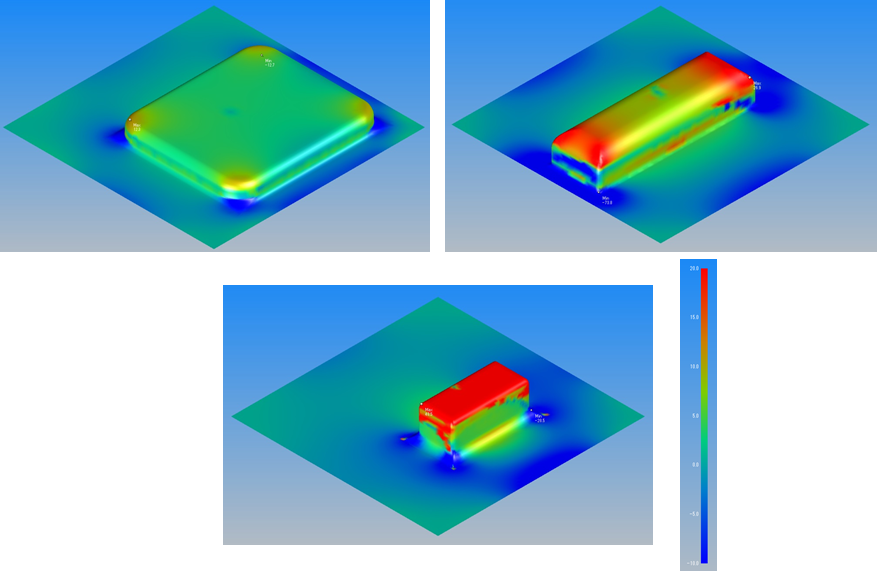
図1.角筒絞り加工シミュレーション結果の例
注)コンターは板厚減少率(%)を表しています.赤い部分は板厚が大きく減少しています.
有限要素法,ワンステップ法についての詳細は下記をご参照下さい.
「基本からわかる有限要素法」
http://www.morikita.co.jp/books/book/2391
「01_ソリューション紹介:構造解析がさらに高精度に!加工硬化の影響をとりこむHYCRASH」
http://ls-dyna.jsol.co.jp/newsletter/25_01.html#3
訓練データ,テストデータの作成
角筒形状をランダムに変化させて11000回のプレス加工シミュレーションを実行しました.(訓練用:10000,テスト用:1000)具体的には図2に示す寸法を変化させています.外形は100x100で固定し,残り8つの寸法を0.1mm単位で変化させています.角筒形状は1つだけです.各寸法には上限値と下限値をを設けましたが,形状パターンは約2x10^18通りもあります.手動では11000回もシミュレーションを行えないので,形状作成から結果抽出までを自動化しました.
シミュレーション結果の学習
ニューラルネットワーク(AI)
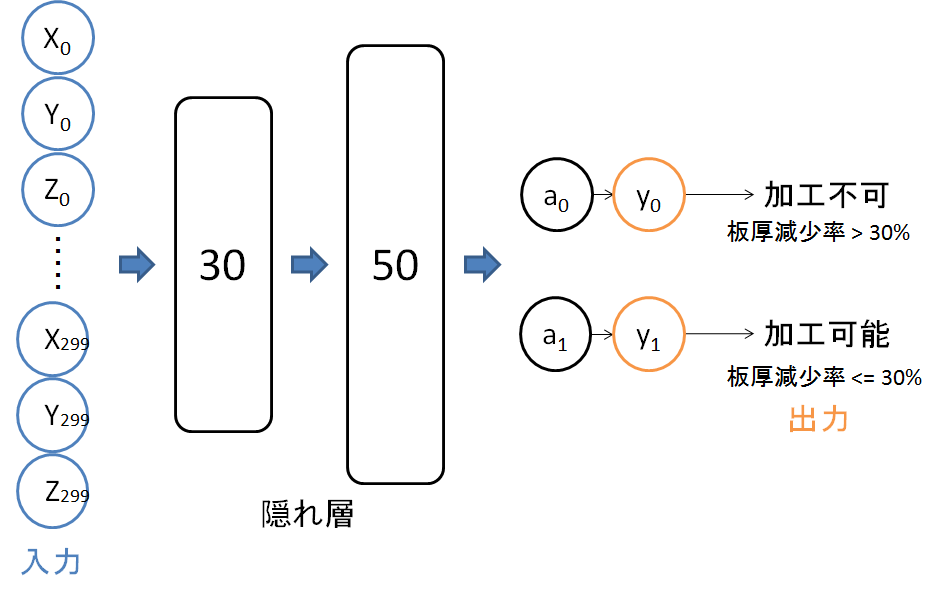
図3に示す構造のニューラルネットワーク(AI)を作成し,シミュレーション結果を学習させました.このAIは形状を与えると,板厚減少率の最大値が30%を超えるか,超えないかを判断してくれます.この判定が正確に出来ればベテラン技術者の直観を再現出来たことになります.まだ角筒絞り加工に対してだけですが...(^_^;)
AIの作成では下記の書籍を参考にしました.
「ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装」
https://www.oreilly.co.jp/books/9784873117584/
AIに形状を与える方法
最初はAIに形状を表すデータとして図2の寸法値を与えていたのですが,直ぐに問題に気づきました.AIは入力データの数を固定しなければならないのですが,寸法の数は形状が変わると変化してしまいます.例えば,2つの角筒を成形する場合は,1つの角筒に対して寸法の数は2倍になります.つまり寸法値を入力データとするAIは汎用性がありません.
そこで,節点数(形状を表す代表点)を300点で固定し,各節点の座標をAIの入力データとしました.節点の与え方は形状の特徴がなるべく残るようなアルゴリズムを使用しています.図4は入力データを可視化したものです.この方法なら図4の右図の様な形でもAIは読み込むことができます.ただし,今回は角筒が1つの場合のみとしましたので,図4の右図の様な形状は学習データ,テストデータに入っていません.
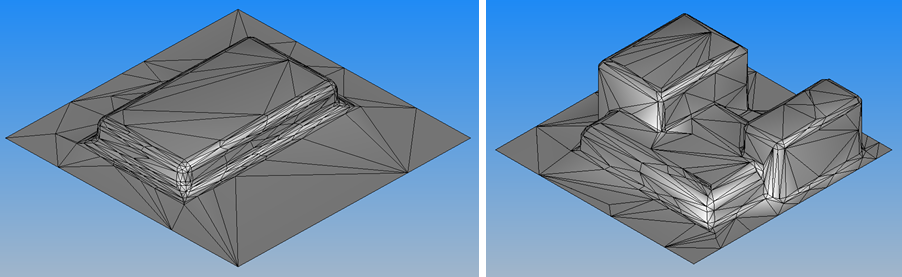
図4.入力データを可視化した例(節点数300点)
シミュレーション用のメッシュ(節点の集まり)は別で用意します.節点数が300点では粗すぎて精度の良いシミュレーションが行えません.
AIの学習フロー
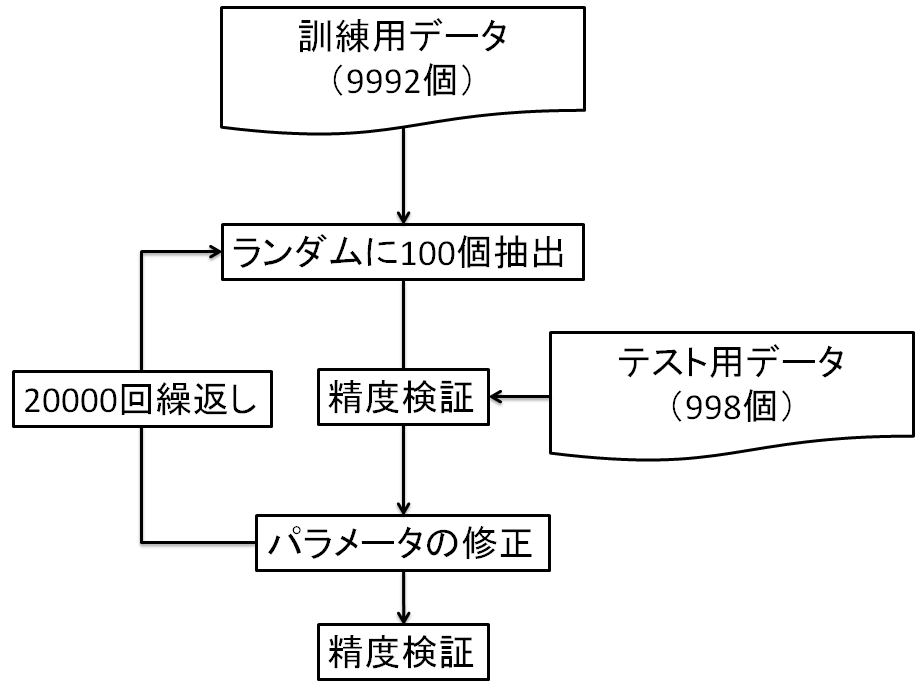
図5に学習フローを示します.訓練データからランダムに100個抽出します.訓練データと辻褄が合うように,AIのパラメータを更新します.パラメータの更新は20000回行いました.パラメータを更新する度にテストデータを用いて精度検証を行います.訓練データとテストデータの数が中途半端になっているのは,シミュレーションでエラーが発生したデータを除いたためです.
精度検証
正解率は96%
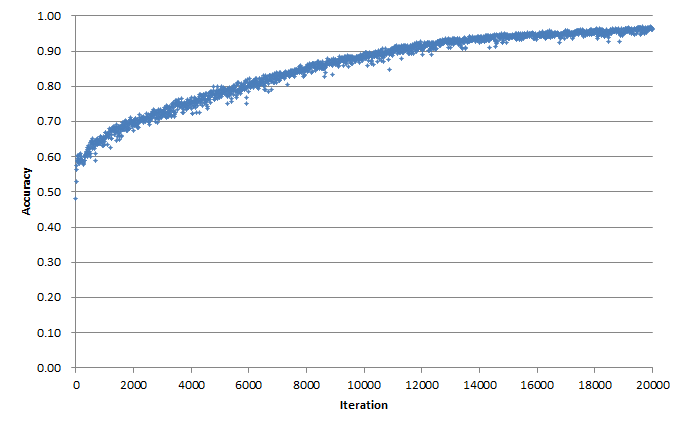
図7はテストデータに対する正解率と学習回数の関係を示しています.約96%の確率で正しく加工可否の判断が出来る様になりました.
課題と所感
スケールアップするとシミュレーションの自動化が大変
精度の良いAIを作るためには,膨大なデータが必要です.今回は簡単な形状で,境界条件(荷重とか固定とか)も必要無いシミュレーションでしたので,シミュレーションの連続実行の自動化(データ収集の自動化)が簡単でした.しかし,もっと複雑なシミュレーションになりますと自動化がとても大変です.
一方で1度自動化できてしまえば,時間に比例してデータが溜まっていきますので,AIはどんどん賢くなります.シミュレーションの自動化は課題であると同時に解決できれば大きなメリットになります.
シミュレーションの精度
シミュレーション結果が現実と全然違っていては,それをAIに学習させても仕方がありません.シミュレーションを連続実行する前に,シミュレーション結果と現実との相関を確認しておく必要があります.
AIに形状を与える方法はもっといいやり方があるはず
今回は節点数を固定した上で,形状の特徴がなるべく残るように節点を選択し,その座標をAIに与えました.この方法だと形状が変わると各節点の相対的な位置関係が変化してしまいます.節点付与には同じアルゴリズムを使用しているとは言え,もっと良い方法があると思います.
終わりに
10年後には設計業務のルーチンワークはAIがやってくれるようになるかもしれません.そんな未来に向けた取り組みがもっと増えたらいいなぁと思ってこの記事を書きました.ご意見,ご質問等ございましたらコメント欄にお願い致します.
Yu-Nie
Appendix
訓練データとテストデータは節点座標と板厚減少率の最大値を記録したCSVファイルです.下記からダウンロードできます.
訓練データ,テストデータ
各行が形状と解析結果のセットになります.
0~900列:節点の座標(形状)
901列 :板厚減少率の最大値(解析結果)
902列 :ラベル(板厚減少率が30%以下⇒1,30%より大きい⇒0)
今回使用したAIのソースコードは下記からダウンロードできます.
Jack_for_qiita.py
# -*- coding: utf-8 -*-
"""
Created on Mon Oct 17 08:54:14 2016
@author: izumiy
The MIT License (MIT)
Copyright (c) 2016 Koki Saitoh
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
"""
import numpy as np
from collections import OrderedDict
import pickle
"""========================================================================="""
"""レイヤを生成するクラス"""
"""========================================================================="""
"""Affineレイヤの順伝播と逆伝播を求めるクラス======================================="""
class Affine:
def __init__(self, W, b):
self.W = W # パラメータ
self.b = b # バイアス
self.x = None # 入力
self.dW = None # パラメータの勾配
self.db = None # バイアスの勾配
self.original_x_shape = None
def forward(self, x):
self.original_x_shape = x.shape # ベクトルに変換する前のxの形状を記録する
x = x.reshape(x.shape[0], -1) # xが3次元以上の場合,ベクトルに変換する.x.shape[0] = データ数
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T) # W.TはWの転置
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis = 0)
dx = dx.reshape(*self.original_x_shape) # 入力データの形状に戻す(テンソル対応)
return dx
"""SoftMaxレイヤの順伝播と逆伝播を求めるクラス====================================="""
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 1入力当たりの誤差
self.y = None # softmaxの出力
self.t = None # 正解出力のnp配列(ラベル表現(1xデータ数))
def forward(self, x, t):
self.t = t
self.y = softmax_for_matrix(x) # 入力データが複数ある場合, x = (データ数, 要素数)
# self.y = softmax(x) # 入力データが1つの場合, x = (1, 要素数)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 教師データがone-hot-vectorの場合
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
"""Reluレイヤの順伝播と逆伝播を求めるクラス===========================================
# x:入力のnp配列,dout:出力層の勾配"""
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy() # outにxをコピー
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
# test Relu
# x = np.array([[1.0, -0.5],
# [-2.0, 3.0]])
# y = Relu()
# a = y.forward(x)
# print(a)
# [[ 1. 0.]
# [ 0. 3.]]
# b = y.backward(a)
# print(b)
# [[ 1. 0.]
# [ 0. 3.]]
"""Sigmoidレイヤの順伝播と逆伝播を求めるクラス========================================
# x:入力のnp配列,dout:出力層の勾配"""
class Sigmoid:
def __init__(self):
self.out = None # 順伝播の出力
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
# test Sigmoid
# x = np.array([[1.0, -0.5],
# [-2.0, 3.0]])
# y = Sigmoid()
# a = y.forward(x)
# print(a)
# [[ 0.73105858 0.37754067]
# [ 0.11920292 0.95257413]]
# b = y.backward(x)
# print(b)
# [[ 0.19661193 -0.11750186]
# [-0.20998717 0.13552998]]
"""畳み込み層を生成するクラス===================================================="""
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中間データ(backward時に使用)
self.x = None
self.col = None
self.col_W = None
# 重み・バイアスパラメータの勾配
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape # filter_num, input_channel_num, filter_height, filter_width
N, C, H, W = x.shape # input_num, input_channel_num, input_height, input_width
out_h = int(1 + (H + 2*self.pad - FH) / self.stride) # out_h:出力データの高さ, H:入力データの高さ, pad:パディング幅, FH:フィルターの高さ, stride:ストライド,フィルターを適用する位置の間隔
out_w = int(1 + (W + 2*self.pad - FW) / self.stride) # out_hとout_wが整数になるように,pad, FH, strideを指定する
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
"""プーリング層を生成するクラス===================================================="""
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H + 2*self.pad - self.pool_h) / self.stride) # out_h:出力データの高さ, H:入力データの高さ, pad:パディング幅, pool_h:フィルターの高さ, stride:ストライド,フィルターを適用する位置の間隔
out_w = int(1 + (W + 2*self.pad - self.pool_w) / self.stride) # out_hとout_wが整数になるように,pad, FH, strideを指定する
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
"""ドロップアウト層を生成するクラス=================================================="""
class Dropout:
"""
http://arxiv.org/abs/1207.0580
"""
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg: # 学習
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else: # テスト
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
"""========================================================================="""
"""画像⇔行列の変換を行う関数"""
"""========================================================================="""
"""画像を行列へ変換する関数===================================================="""
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : (データ数, チャンネル, 高さ, 幅)の4次元配列からなる入力データ
filter_h : フィルターの高さ
filter_w : フィルターの幅
stride : ストライド
pad : パディング
Returns
-------
col : 2次元配列
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
"""行列を画像へ変換する関数===================================================="""
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
col :
input_shape : 入力データの形状(例:(10, 1, 28, 28))
filter_h :
filter_w
stride
pad
Returns
-------
"""
N, C, H, W = input_shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
"""========================================================================="""
"""ファイル入出力を行う関数"""
"""========================================================================="""
"""インプットと正解出力を読み込む関数=============================================="""
def input_read(file_name):
input = np.loadtxt(file_name, delimiter = ",", usecols = (0, 1, 2, 3, 4, 5, 6, 7))
return input
def label_read(file_name):
label = np.loadtxt(file_name, delimiter = ",", usecols = (9,), dtype = np.int)
return label
def input_read_for_node(file_name):
input_date_list = range(900) # 1~900列を読込む
input_date_tuple = tuple(input_date_list)
input = np.loadtxt(file_name, delimiter = ",", usecols = input_date_tuple)
return input
def label_read_for_node(file_name):
label = np.loadtxt(file_name, delimiter = ",", usecols = (901,), dtype = np.int) # 902列を読込む
return label
"""========================================================================="""
"""損失関数の値を求める関数"""
"""========================================================================="""
"""二乗和誤差を求める関数======================================================"""
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
# test mean_squared_error(y, t)
# t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# print(mean_squared_error(np.array(y), np.array(t)))
# 0.0975
"""交差エントロピー誤差を求める関数==================================================
# y:ニューラルネットワークのアウトプット np配列(データ数xラベル数)
# t:正解出力のone-hot表現 np配列(データ数xラベル数)"""
def cross_entropy_error_one_hot(y, t):
delta = 1e-7
if y.ndim == 1: # 配列の次元数が1の時
t = t.reshape(1, t.size) # .sizeは配列の要素数を求める
y = y.reshape(1, y.size)
batch_size = y.shape[0] # y.shape[0]は配列yの行数 = yのデータ数
return -np.sum(t * np.log(y + delta)) / batch_size #np.log(0)はマイナス無限大になってしまうため,微小な値deltaを追加してマイナス無限大を発生させないようにする
# test cross_entropy_error_one_hot(y, t)
# t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# print(cross_entropy_error_one_hot(np.array(y), np.array(t)))
# 0.510825457099
""" 交差エントロピー誤差を求める関数=================================================
# y:ニューラルネットワークのアウトプット np配列(データ数xラベル数)
# t:正解出力のone-hot表現 np配列(1xデータ数)"""
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size) # .sizeは配列の要素数を求める
y = y.reshape(1, y.size)
batch_size = y.shape[0] # データ数を取得
return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size
# test cross_entropy_error(y, t)
# t = [2]
# y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# print(cross_entropy_error(np.array(y), np.array(t)))
# 0.510825623766
"""========================================================================="""
"""活性化関数"""
"""========================================================================="""
"""np配列をソフトマックス関数値に変換する関数==========================================
# a:np配列, aはベクトル限定, 2次元配列は非対応"""
def softmax(a):
c = np.max(a) # np配列aの最大要素を取得
exp_a = np.exp(a - c) # オーバーフロー対策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
# test softmax(a)
# a = np.array([0.3, 2.9, 4.0])
# y = softmax(a)
# print(y)
# [ 0.01821127 0.24519181 0.73659691]
# print(np.sum(y))
# 1.0
"""np配列をソフトマックス関数値に変換する関数==========================================
# a:np配列, aは2次元配列"""
def softmax_for_matrix(a):
count = 0
y = np.zeros_like(a)
for a_row in a:
c = np.max(a_row) # np配列aの最大要素を取得
exp_a_row = np.exp(a_row - c) # オーバーフロー対策
sum_exp_a_row = np.sum(exp_a_row)
y[count,:] = exp_a_row / sum_exp_a_row
count += 1
return y
# test softmax(a)
# a = np.array([[0.3, 2.9, 4.0],
# [0.2, 3.0, 4.3],
# [0.3, 2.0, 6.0]])
# y = softmax(a)
# print(y)
# [[ 0.01821127 0.24519181 0.73659691]
# [ 0.01285596 0.21141172 0.77573232]
# [ 0.00327502 0.0179273 0.97879767]]
"""========================================================================="""
"""数値微分によって勾配を求める関数"""
"""========================================================================="""
"""多層のニューラルネットワークのパラメータの勾配を求める関数,数値微分=======================
# net:多層のニューラルネットワーククラス, params_W:勾配を求めるパラメータ, rows_W:パラメータの行数
# columns_W:パラメータの列数, x:入力, t:正解出力(ラベル表現)"""
def numerical_gradient_for_multi_net_W(net, params_W, rows_W, columns_W, x, t):
h = 1e-4 # 0.0001
grad_W = np.zeros_like(params_W) # params_Wと同じ形状の配列を生成
for row in range(0, rows_W):
for column in range(0, columns_W):
tmp_val = params_W[row, column]
# f(x+h)の計算
params_W[row, column] = tmp_val + h
fxh1 = net.loss(x, t) # 交差エントロピー誤差
# f(x-h)の計算
params_W[row, column] = tmp_val - h
fxh2 = net.loss(x, t) # 交差エントロピー誤差
grad_W[row, column] = (fxh1 - fxh2) / (2*h)
params_W[row, column] = tmp_val
return grad_W
"""多層のニューラルネットワークのバイアスの勾配を求める関数,数値微分========================
# net:多層のニューラルネットワーククラス, params_b:勾配を求めるバイアス,
# columns_b:バイアスの列数, x:入力, t:正解出力(ラベル表現)"""
def numerical_gradient_for_multi_net_b(net, params_b, columns_b, x, t):
h = 1e-4 # 0.0001
grad_b = np.zeros_like(params_b) # net.Wと同じ形状の配列を生成
for column in range(0, columns_b):
tmp_val = params_b[column]
# f(x+h)の計算
params_b[column] = tmp_val + h
fxh1 = net.loss(x, t)
# f(x-h)の計算
params_b[column] = tmp_val - h
fxh2 = net.loss(x, t)
grad_b[column] = (fxh1 - fxh2) / (2*h)
params_b[column] = tmp_val
return grad_b
# test numerical_gradient and backprop_gradient
# network = TwoLayerNet(input_size = 7, hidden_size = 14, output_size = 2)
# input = np.array([])
# label = np.array([])
# input = input_read()
# label = label_read()
# grad_numerical = network.numerical_gradient_for_multi_net(input, label)
# grad_backprop = network.gradient(input, label)
# print(grad_numerical)
# print(grad_backprop)
# for key in grad_numerical.keys():
# diff = np.average(np.abs(grad_backprop[key] - grad_numerical[key]))
# print(key + ":" + str(diff))
# b1:7.34990135764e-08
# b2:1.44404453672e-11
# W1:5.60468518899e-05
# W2:9.17962625938e-12
"""========================================================================="""
"""パラメータの更新方法"""
"""========================================================================="""
"""SGD"""
class SGD:
def __init__(self, lr=0.0005):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
"""Momentum"""
class Momentum:
def __init__(self, lr=0.0005, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
"""AdaGrad"""
class AdaGrad:
def __init__(self, lr=0.0005):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
"""Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
class Nesterov:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
"""RMSprop"""
class RMSprop:
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
"""========================================================================="""
"""ニューラルネットワークを生成するクラスと学習を実行する関数"""
"""========================================================================="""
"""マルチレイヤのニューラルネットワークを生成するクラス======================================
input_size:入力サイズ,hidden_size_list:隠れ層のニューロンの数のリスト(ex. [100, 100, 100]),output_size:出力サイズ,
activation:活性化関数の選択'relu' or 'sigmoid',
weight_init_std:重みの標準偏差を指定(ex. 0.01),
'relu'または'he'を指定した場合は「Heの初期値」を設定
'sigmoid'または'xavier'を指定した場合は「Xavierの初期値」を設定
weight_decay_lambda:Weight Decay(L2ノルム)の強さ
"""
class MultiLayerNet:
def __init__(self, input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu', weight_decay_lambda = 0):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list) # 隠れ層の数を取得
self.weight_decay_lambda = weight_decay_lambda
self.params = {}
"""重みの初期化"""
self.__init_weight(weight_init_std)
"""レイヤの生成"""
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu} # ディクショナリー"activation_layer"に"Sigmoidレイヤクラス"と"Reluレイヤクラス"を格納
self.layers = OrderedDict()
# 隠れ層の生成
for idx in range(1, self.hidden_layer_num + 1): # idx = 1 ~ hidden_layer_num
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
self.layers['Activation_function' + str(idx)] = activation_layer[activation]() # クラスを生成するので末尾に"()"が必要
# 最後のAffinレイヤの生成.Affinレイヤは全部で hidden_layer_num + 1 個ある
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
# 出力層
self.last_layer = SoftmaxWithLoss()
def __init_weight(self, weight_init_std):
"""重みの初期値設定
weight_init_std : 重みの標準偏差を指定(e.g. 0.01)
'relu'または'he'を指定した場合は「Heの初期値」を設定
'sigmoid'または'xavier'を指定した場合は「Xavierの初期値」を設定
"""
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size] # hidden_size_list の前後に self.input_size と self.output_size を追加する
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'): # str(ABC).lower() ⇒ "ABC"を"abc"に変換する
scale = np.sqrt(2.0 / all_size_list[idx - 1]) # ReLUを使う場合に推奨される初期値
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'): # weight_init_std が sigmoid または xavier だった場合,
scale = np.sqrt(1.0 / all_size_list[idx - 1]) # sigmoidを使う場合に推奨される初期値
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx]) # 各層の 入力要素数,出力要素数
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay # 損失関数に荷重減衰(weight_decay)を加算する
# y:ニューラルネットワークの出力,t:正解ラベル
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1) # 最大値となる要素のインデックスを求める.
if t.ndim != 1 : t = np.argmax(t, axis=1) # One-Hot形式の場合はラベル形式に変換する.
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
"""数値微分"""
def numerical_gradient_for_multi_net(self, x, t):
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size] # hidden_size_list の前後に self.input_size と self.output_size を追加する
grads = {}
for idx in range(1, self.hidden_layer_num + 2):
grads['W' + str(idx)] = numerical_gradient_for_multi_net_W(self, self.params['W' + str(idx)], all_size_list[idx - 1], all_size_list[idx], x, t)
grads['b' + str(idx)] = numerical_gradient_for_multi_net_b(self, self.params['b' + str(idx)], all_size_list[idx], x, t)
return grads
"""誤差逆伝播法"""
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 勾配の保存
grads = {}
for idx in range(1, self.hidden_layer_num + 2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grads
# 学習済みパラメータの保存
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
"""マルチレイヤのニューラルネットの学習の実行する関数=================================="""
def carry_out_MultiLayerNet():
print("Start calculation MultiLayerNet")
network = MultiLayerNet(input_size = 900, hidden_size_list = [30, 50], output_size = 2)
# input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu', weight_decay_lambda = 0
# input_size:インプットの要素数, hidden_size_list:隠れ層のニューロンの数のリスト(ex. [100, 100, 100]), output_size:出力層の要素数
"""パラメータの更新方法の選択"""
# optimizer = SGD(lr = 0.0005)
# optimizer = Momentum(lr = 0.0005, momentum = 0.9)
# optimizer = AdaGrad(lr = 0.0005)
optimizer = Adam(lr = 0.0001)
# データのインポート, データはJack.pyと同じディレクトリに保存しておくこと
input_train = np.array([])
label_train = np.array([])
input_test = np.array([])
label_test = np.array([])
input_train = input_read_for_node("node_for_train.csv") # 訓練データの読込:入力
label_train = label_read_for_node("node_for_train.csv") # 訓練データの読込:正解出力
input_test = input_read_for_node("node_for_test.csv") # テストデータの読込:入力
label_test = label_read_for_node("node_for_test.csv") # テストデータの読込:正解出力
iters_num = 20001 # 学習回数
train_size = input_train.shape[0] # データ数
batch_size = 100 # バッチサイズ
# learning_rate = 0.0005 # 学習率
grads = {}
train_loss_list = [] # 交差エントロピー誤差の推移を記録するリスト
train_acc_list = [] # ニューラルネットワークの正解率の推移を記録するリスト
test_acc_list = []
# iter_per_epoch = max(train_size / batch_size, 1)
iter_per_epoch = 10 # 学習回数 = iter_per_epochの時に精度検証を行う
for i in range(iters_num): # 0, 1, 2, ... , iters_num-1
print("iteration number = " + str(i))
batch_mask = np.random.choice(train_size, batch_size)
input_batch = input_train[batch_mask]
label_batch = label_train[batch_mask]
grads = network.gradient(input_batch, label_batch) # 誤差逆伝播法による勾配計算
# grads = network.numerical_gradient_for_multi_net(input_batch, label_batch) # 数値微分による勾配計算
optimizer.update(network.params, grads)
# for key in ('W1', 'b1', 'W2', 'b2'):
# network.params[key] -= learning_rate * grad[key]
loss = network.loss(input_batch, label_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(input_train, label_train)
test_acc = network.accuracy(input_test, label_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("loss = " + str(loss))
print("train_loss_list:" + str(train_loss_list))
print("train_acc_list:" + str(train_acc_list))
print("test_acc_list:" + str(test_acc_list))
# 学習結果のエクスポート
np.savetxt("train_loss_list.csv", train_loss_list, delimiter = ",")
np.savetxt("train_acc_list.csv", train_acc_list, delimiter = ",")
np.savetxt("test_acc_list.csv", test_acc_list, delimiter = ",")
for key in ('W1', 'b1', 'W2', 'b2', 'W3', 'b3'): # Wとbの数はhidden_size_listに応じて変わる
print(str(key))
print(network.params[key].shape)
print(network.params[key])
network.save_params("params.pkl")
print("end caluculation")
return 0
"""========================================================================="""
"""main"""
"""========================================================================="""
if __name__ == '__main__':
start = carry_out_MultiLayerNet()