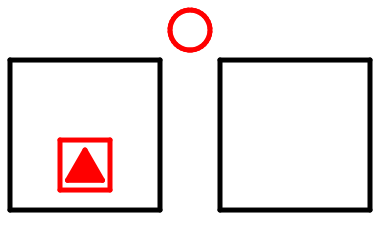
型レベルで平衡が保証される探索木
はじめに
ほかの言語でハッシュテーブルを使うような辞書構造を実現するのにHaskellでは状態変化をともなわない重み平衡木を使うということを説明した。
木を変化させるときに左右の木が持つ要素数の比を3以下におさえることで木の平衡を保ち探索効率が低下しないようにしている。しかし、モジュールの内部では不均衡な木を作ることは可能だ。Haskellの型システムをうまく利用することで型レベルで均衡が保証された木構造を作成することができる。BB木(Binary B-tree)という構造を利用する。
BB木とは
2-3木と呼ばれることもある。2-3木と呼ばれる木が2通りある。要素を葉に持つ構造とノードに持つ構造だ。混乱を避けるために前者を2-3木と呼び後者をBB木と呼ぶ。
探索の効率
均衡のとれた探索木に対する探索はO(log n)だ。木が不均衡になっていくにつれて探索の効率は悪化していきO(n)に近づいていく。
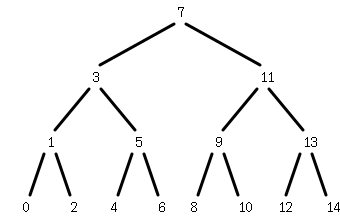
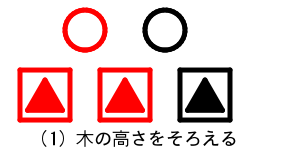
高さのそろった2分木
つねに高さのそろった2分木であれば探索の効率はO(log n)に保たれる。
しかしこのような木では要素数0, 1, 3, 7, 15, 31, 63 ...のように、木の高さnに対して正確に2 ^ n - 1個の要素を持つ構造しか作ることができない。
BB木
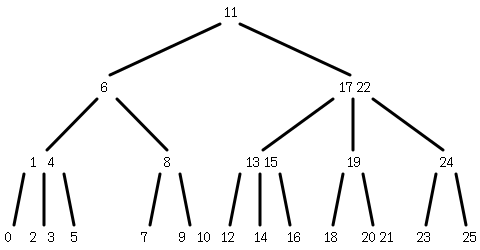
高さがそろっているという条件を変えることなく任意の要素数を持つ木を作るにはどうすれば良いだろうか。2分木では2分岐のみしか許されないところを2分岐と3分岐のどちらかで良いというように制限をゆるめてやる。そうすると任意の要素数の高さのそろった木を作ることができる。
図では26個の要素を持つ木が示されている。この図では省略しているが末端の要素はその下に「高さ0の木」を子として持っている。
BB木に対する検索、値の追加、値の削除について見ていこう。
検索
検索は簡単だ。2分探索木とほとんど同じだ。ノードの値と見つけようとしている値との比較でどの枝に進むかを選べば良い。2分探索木との違いは、値が2つあり枝が3つあるノードがあるということだ。これについては小さいほうの値より小さければ左の木に、2つの値のあいだについてはまん中の枝に大きいほうの値より大きければ右の木に、それぞれ進めば良い。
追加
追加すべき位置をみつけて葉である「高さ0の木」を「追加する値のみを要素とする高さ1の木」に変換する。その後は木を高くするという操作を根にむかって連鎖していけばいい。この連鎖は値1つのノード(2分岐のノード)に到達するまで続く。1番上のノード(根)に到達するまでに2分岐のノードが存在しなければ木全体が1高くなることになる。
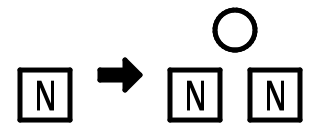
高さ0の木を高さ1の木にする
検索と同様の手順で木をたどっていき枝のさきにある「高さ0の木」までたどる。そしてそれを上図のように追加する値のみを含む「高さ1の木」におきかえる。
「木を高くする」の連鎖
「値の追加」によって枝の高さが左、まん中、右のいずれかが1だけ高くなる。もし2分岐のノードであれば3分岐のノードにすることによって高さをならすことができる。もともと3分岐のノードであればそれを1だけ高い木におきかえて、「木を高くする」処理を上に伝播させる。
対称性を考慮すると、子となる枝の高さが高くなるような3通りの場合がある。
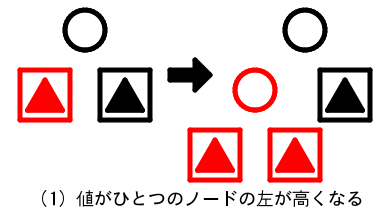
- 2分岐(値がひとつ)のノードの左の枝が高くなる
- 3分岐(値がふたつ)のノードの左の枝が高くなる
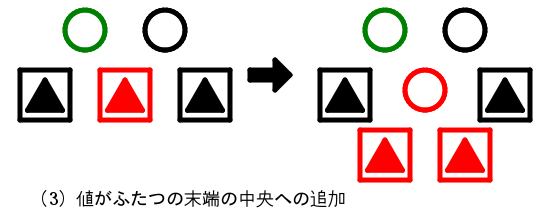
- 3分岐(値がふたつ)のノードのまん中の枝が高くなる
それぞれについてどのような処理となるか見ていこう。
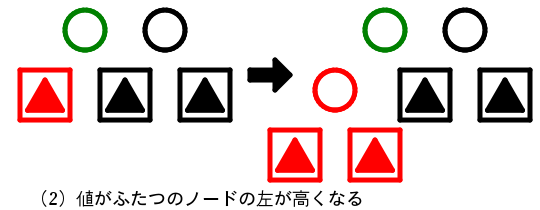
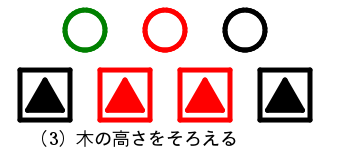
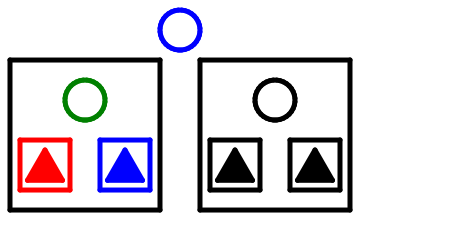
赤で示された左の枝の高さが高くなった。
2分岐のノードを3分岐のノードにすることで木の高さがそろう。このとき「木を高くする」処理の連鎖はここで終了する。
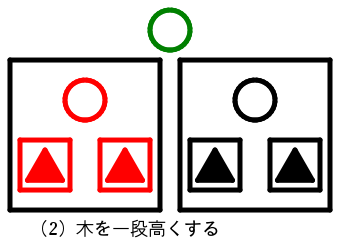
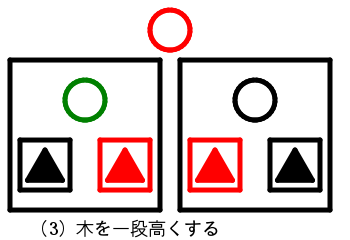
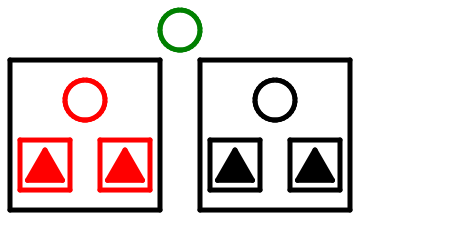
3分岐のノードの左が高くなった。
木の高さをそろえたがこれは値が3つの4分岐のノードとなってしまう。
全体を1段高くすることによって条件を満たす木となる。木が高くなったので「木を高くする」処理は上に伝播する。
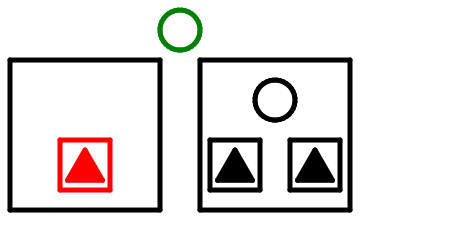
やはり4分岐のノードになってしまう。
木を高くする。「木を高くする」処理は上に伝播する。
このようにして木の平衡を失わずに値を追加することができる。
削除
値の削除は追加よりもすこしだけ複雑だ。末端の要素を削除するということは木を1段低くするということだ。「木を低くする」という処理が上にむかって連鎖していく。枝のうちひとつが低くなったとき2つの処理のどちらかが行われる。
- 隣りが3分岐のとき「木の回転」によって値と枝を融通してもらう
- 隣りが2分岐のとき上から値を融通してもらい隣りと融合させる
上からの値の融通のとき上のノードが3分岐のノードであれば2分岐のノードとなり2分岐のノードであれば「木を低くする」処理が上に伝播する。
隣りから融通
左の枝が低くなる前の状態だ。
左の枝が低くなった。
木の回転にやって均衡が回復する。
上から融通
隣りの枝が2分岐のノードである。
左の枝が1段低くなった。
上から値を融通してもらう。上のノードが2分岐ならば全体として木は低くなる。上のノードが3分岐のときは2分岐となりこの木が左右どちらかの枝となる。
途中のノードからの削除
木の高さを低くする処理が下から上に向かって連鎖する様子を見た。この処理によって末端のノードからの削除ができる。しかし途中のノードからの削除はこれだけではできない。途中のノードからの削除は以下のようにして末端のノードからの削除におきかえる。
- その値の左の枝を最大値と残りの木にわける
- この処理自体は値の削除とほぼ同じ操作で可能だ
- 削除する値をその最大値でおきかえる
- 木が低くなるようであれば「木を低くする」処理を連鎖させる
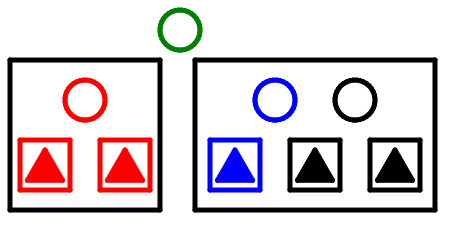
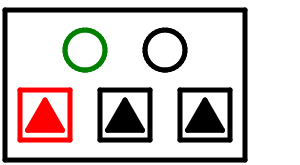
緑の値を削除する前の状態だ。
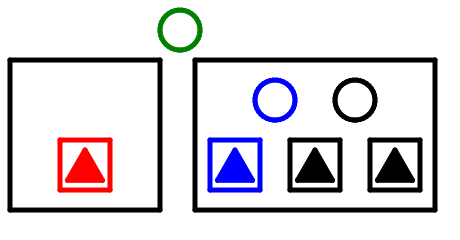
赤で示した左の枝を最大値とそれ以外の木にわける。木の高さが変わらないときと低くなるときとがある。
最大値で削除する値をおきかえる。木の高さが変化しないものについてはそれで終わりである。木が低くなるものについては隣りや上からの融通の操作を続ける。
コード - 命名規則
値や枝の位置について混乱しやすいので、それらの位置を統一的な変数で示すことにする。
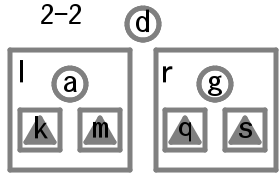
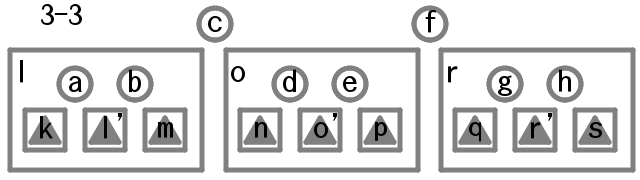
2分岐のときの根の値をdとし左右の枝をそれぞれl, rとする。左の枝について2分岐であれば値をaとし左右の枝をそれぞれk, mとする。右の枝についても2分岐であれば値をgとし左右の枝をそれぞれq, sとする。
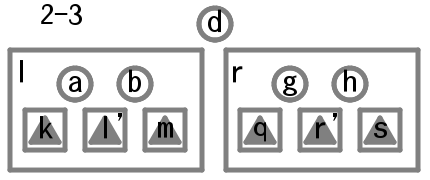
左の枝が3分岐であればふたつの値をそれぞれa, bとしみっつの枝をそれぞれk, l', mとする。右の枝についても3分岐であればふたつの値をそれぞれg, hとしみっつの枝をそれぞれq, r', sとする。
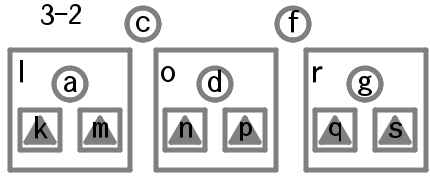
3分岐のときふたつの根の値をそれぞれc, fとし、左、まん中、右の枝をそれぞれl, o, rとする。まん中の枝が2分岐ならその値をdとし左右の枝をそれぞれn, pとする。
まん中の枝が3分岐のときふたつの値をそれぞれd, eとし左、まん中、右の枝をそれぞれn, o', pとする。
また上記の規則とは別に枝l, o, rが変化したあとの値をそれぞれl', o', r'と表すこともある。
コード - 単相版
まずはシンプルなものから説明するということで辞書ではなく集合のコードを示す。また、多相的な要素を持たせるには言語拡張が必要なので、まずは単相型の例から見ていこう。Int型の集合とする。
モジュール宣言など
{-# LANGUAGE TupleSections #-}
module SetBM (Set, empty, member, insert, delete) where
TupleSections拡張はトリビアルなものだ。演算子は(+ a)のような部分適用が可能だが同じようにタプルでも(, a)のような表記を可能にする。モジュール名はSetBM(Binary b-treeによるMonomorphicなSet)とし公開する型、値、関数は集合としての典型的なインターフェースだ。
型の定義
type Set = Tree ()
data Tree a = Zero a | Succ (Tree (Node a)) deriving Show
data Node a = Nd2 a Int a | Nd3 a Int a Int a deriving Show
Treeに型引数としてユニット型をあたえたものを集合(Set)として扱う。ユニット型は空(高さ0)の木の表現だ。
Node型はNd2とNd3のふたつの値構築子を持つ。それぞれ2分岐、3分岐のノードを表現する。型変数aが枝を、Intが要素を示す。
型Treeの定義に注目!ここに「型レベルで高さがそろう」仕組みがある。
Tree ()はZero ()またはSucc (Tree (Node ()))だ。Node ()は高さ1の木だ。Tree (Node ())はZero (Node ())かSucc (Tree (Node (Node ())))だ。
Succがいくつか続いてZeroがきてそのあとに実際の木の構造がくる。Succの数が木の高さになる。Node (Node (Node ...))のような形の木は高さがそろった木である。そして高さ0の木、高さ1の木、高さ2の木...といった高さの異なる木をひとつの型で表現するためにTree型がある。
空集合
empty :: Tree ()
empty = Zero ()
空集合は高さ0の木で表現される。高さ0の木の直接的な表現は()(ユニット値)であるが、異なる高さの木と同じ型としてまとめるために型Treeの値構築子ZeroでTree ()型に変換している。
型クラス
高さ2の木はNode (Node ())と表せる。高さ1の木はNode ()として表せる。高さが1以上の木はNode xの形で表現できる。しかし高さ0の木は()でありNode xの形で表現されない。高さ0の木に対する演算を高さ1以上の木と統一的に扱うためには木に対する演算を型クラスのメンバ関数とする必要がある。
また、型クラスなしにNode xに対する演算を定義しようとすると型がNode (Node (Node ...のように無限に続いてしまいうまく型づけできない。
理由はともかく、型クラスのメンバ関数とすれば「うまくいく」。
class IsNode a where
mem :: Int -> a -> Bool
ins :: Int -> a -> Either a (a, Int, a)
del :: Int -> Node a -> Either (Node a) a
mx :: Node a -> (Int, Either (Node a) a)
関数memは集合に含まれるかどうかを教える。
関数insは値を追加する関数だが返り値がすこし複雑だ。Either型によって木の高さが変わらないもの(Left値)と木の高さが高くなるもの(Right値)とを示している。扱いやすさのため「木の高さが高くなるもの」についてはNodeとしてまとめず(左の枝、値、右の枝)のタプルとして返すようにした。
関数delは値を削除する。削除される木の型をaではなくNode aとしていることに注意する。結果として低くなった木をa型の値として表現したいからだ。関数insと同じようにEither型によって結果の木の高さの違いを表現している。
関数mxは関数delと似ている。これは木の最大値とそれを削除した残りの木とをタプルとして返す。
ユニット値はNodeである
型ユニットを型クラスIsNodeのインスタンスにしよう。
instance IsNode () where
mem _ _ = False
ins v _ = Right ((), v, ())
del v t@(Nd2 _ d _)
| v == d = Right ()
| otherwise = Left t
del v t@(Nd3 _ c _ f _)
| v == c = Left $ Nd2 () f ()
| v == f = Left $ Nd2 () c ()
| otherwise = Left t
mx (Nd2 _ d _) = (d, Right ())
mx (Nd3 _ c _ f _) = (f, Left $ Nd2 () c ())
空の集合にはどんな値も含まれないのでmemは必ずFalseとなる。空(高さ0)の木に値を追加すると左右に空の木を持つ木となる。2分岐で高さ1の木から要素を削除したら空の木になる。3分岐の木であれば木の高さは変わらずに2分岐の木となる。高さ1の木から最大値をとりだすのもとくに意外性はないだろう。
検索
instance IsNode a => IsNode (Node a) where
mem v (Nd2 l d r)
| v < d = mem v l
| v == d = True
| otherwise = mem v r
mem v (Nd3 l c o f r)
| v < c = mem v l
| v == c = True
| v < f = mem v o
| v == f = True
| otherwise = mem v r
Node aに対してノードに対する演算を実行するためにはaも「ノードである」必要がある。よってIsNode a =>という型制約がつく。関数memは値vとノードの持つ値との大小関係によってTrueを返すかまたはどれかの枝に進むかをふりわけている。
追加
値の大きさによってどれかの枝に値を追加し、結果として枝が高くなるかどうかでさらに処理をわける。
ins v t@(Nd2 l d r)
| v < d = Left $ case ins v l of
Left l' -> Nd2 l' d r
Right (k, a, m) -> Nd3 k a m d r
| v == d = Left t
| otherwise = Left $ case ins v r of
Left r' -> Nd2 l d r'
Right (q, g, s) -> Nd3 l d q g s
もともと2分岐のときには枝が高くなった場合には3分岐のノードとする。
ins v t@(Nd3 l c o f r)
| v < c = case ins v l of
Left l' -> Left $ Nd3 l' c o f r
Right (k, a, m) -> Right (Nd2 k a m, c, Nd2 o f r)
| v == c = Left t
| v < f = case ins v o of
Left o' -> Left $ Nd3 l c o' f r
Right (n, d, p) -> Right (Nd2 l c n, d, Nd2 p f r)
| v == f = Left t
| otherwise = case ins v r of
Left r' -> Left $ Nd3 l c o f r'
Right (q, g, s) -> Right (Nd2 l c o, f, Nd2 q g s)
もともと3分岐のときには枝が高くなったときには全体を高くする。高くなったときには必ず2分岐の木となるがそれを(左の枝、値、右の枝)というタプルとして表現している。
削除
削除する値とノードの値との大小関係によって変形する枝を決める。削除する値とノードの値が等しければ左の枝を最大値とそれ以外の木とにわける。そうでなければ選んだ枝に対して再帰的に削除操作を行い、木が低くなったときには隣りまたは上から値や枝を融通する。
del v (Nd2 l d r)
| v <= d = case if v < d then (d, del v l) else mx l of
(d', Left l') -> Left $ Nd2 l' d' r
(d', Right l') -> case r of
Nd2 q g s -> Right $ Nd3 l' d' q g s
Nd3 q g r' h s -> Left R
Nd2 (Nd2 l' d' q) g (Nd2 r' h s)
| otherwise = case del v r of
Left r' -> Left $ Nd2 l d r'
Right r' -> case l of
Nd2 k a m -> Right $ Nd3 k a m d r'
Nd3 k a l' b m -> Left $
Nd2 (Nd2 k a l') b (Nd2 m d r')
v <= dのときはv < dでは再帰的に削除の処理を行いx == dでは左の木の最大値をとりだす。結果として木の高さが変わらないときには単純におきかえれば良い。木が低くなるときは右の木が2分岐であれば全体を低くし、そうでなければ左回転によって左の木を高くする。
v > dのときはv < dのときと左右対称の操作をすれば良い。
del v (Nd3 l c o f r)
| v <= c = Left $ case if v < c then (c, del v l) else mx l of
(c', Left l') -> Nd3 l' c' o f r
(c', Right l') -> case o of
Nd2 n d p -> Nd2 (Nd3 l' c' n d p) f r
Nd3 n d o' e p ->
Nd3 (Nd2 l' c' n) d (Nd2 o' e p) f r
| v <= f = Left $ case if v < f then (f, del v o) else mx o of
(f', Left o') -> Nd3 l c o' f' r
(f', Right o') -> case l of
Nd2 k a m -> Nd2 (Nd3 k a m c l') f' r
Nd3 k a l' b m ->
Nd3 (Nd2 k a l') b (Nd2 m c o') f r
| otherwise = Left $ case del v r of
Left r' -> Nd3 l c o f r'
Right r' -> case o of
Nd2 n d p -> Nd2 l c (Nd3 n d p f r')
Nd3 n d o' e p ->
Nd3 l c (Nd2 n d o') e (Nd2 p f r')
3分岐の木に対しても同様の操作をする。ただし全体の木を低くするかわりに3分岐の木を2分岐の木にすることになる。
mx (Nd2 l d r) = case mx r of
(u, Left r') -> (u, Left $ Nd2 l d r')
(u, Right r') -> (u ,) $ case l of
Nd2 k a m -> Right $ Nd3 k a m d r'
Nd3 k a l' b m -> Left $ Nd2 (Nd2 k a l') b (Nd2 m d r')
mx (Nd3 l c o f r) = case mx r of
(u, Left r') -> (u, Left $ Nd3 l c o f r')
(u, Right r') -> (u ,) . Left $ case o of
Nd2 n d p -> Nd2 l c (Nd3 n d p f r')
Nd3 n d o' e p -> Nd3 l c (Nd2 n d o') e (Nd2 p f r')
木の最大値をとりだす関数mxは関数delと似ているが、右の枝のみを考えれば良いのでコードはより単純になる。ただし、残りの木だけではなく値も上にわたしていく必要がある。
Tree型に対する操作
Node型に対する操作をラップしてTree型の値に対する操作にする。
member :: IsNode a => Int -> Tree a -> Bool
member v (Zero n) = mem v n
member v (Succ t) = member v t
insert :: IsNode a => Int -> Tree a -> Tree a
insert v (Zero n) = case ins v n of
Left n' -> Zero n'
Right (l, d, r) -> Succ . Zero $ Nd2 l d r
insert v (Succ t) = Succ $ insert v t
delete :: IsNode a => Int -> Tree a -> Tree a
delete v (Succ (Zero n)) = case del v n of
Left n' -> Succ $ Zero n'
Right n' -> Zero n'
delete v (Succ t) = Succ $ delete v t
delete _ t = t
Tree型の値のSuccを削っていき最後のZeroもとったうえでNodeに対する操作を行い、Zeroをつけ、適切な数のSuccをつけて結果とする。
コード - 多相版
TypeFamilies
ここでは詳しくは説明しない。TypeFamilies拡張の機能を使うとインスタンス宣言のなかで型クラスのインスタンスとなる型と別の型とを関連づけることができる。たとえばある型Aが何らかのコンテナであるような場合、型Aの要素が型Bであるような関係をtype Elem A = Bのように表現することができる。いずれTypeFamiles拡張の説明も書く予定だ。
モジュール宣言など
{-# LANGUAGE TupleSections, TypeFamilies #-}
module SetB (Set, empty, member, insert, delete) where
TypeFamilies拡張が使えるようにLANGUAGEプラグマに追加した。
型の定義
type Set v = Tree v (Tip v)
data Tree v a = Zero a | Succ (Tree v (Node v a)) deriving Show
data Node v a = Nd2 a v a | Nd3 a v a v a deriving Show
data Tip v = Tip deriving Show
型Treeや型Nodeに要素を表す型変数vを追加した。単相型の版のIntの部分をvにおきかえた。空の木を表すのにユニット型ではなくTip型を使うようにした。これはInt型の木に対する空の木をTip Int型としDouble型の木に対する空の木をTip Double型のようにして型をあわせるためだ。
空の木
empty :: Tree v (Tip v)
empty = Zero Tip
空(高さ0)の木はTipで表される。Tree型の値構築子ZeroによってTree型に変換している。
命名規則の説明
{-
l d r
+-+-+ +-+-+
| a | | g |
k m q s
l d r
+---+---+ +---+---+
| a | b | | g | h |
k l' m q r' s
l c o f r
+-+-+ +-+-+ +-+-+
| a | | d | | g |
k m n p q s
l c o f r
+---+---+ +---+---+ +---+---+
| a | b | | d | e | | g | h |
k l' m n o' p q r' s
-}
命名規則の説明をコメントとして置いた。
型クラス
class IsNode a where
type Elem a
mem :: Elem a -> a -> Bool
ins :: Elem a -> a -> Either a (a, Elem a, a)
del :: Elem a -> Node (Elem a) a -> Either (Node (Elem a) a) a
mx :: Node (Elem a) a -> (Elem a, Either (Node (Elem a) a) a)
クラス宣言に型族としてElem aを登録した。Elem aはインスタンスとなる型aに対してそれぞれ別個に決めることができる。型aをNodeであると考えたときに要素となる型をElem aとして設定する。
Tip v型はNodeだ
instance Eq v => IsNode (Tip v) where
type Elem (Tip v) = v
mem _ _ = False
ins v _ = Right (Tip, v, Tip)
del v t@(Nd2 _ d _)
| v == d = Right Tip
| otherwise = Left t
del v t@(Nd3 _ c _ f _)
| v == c = Left $ Nd2 Tip f Tip
| v == f = Left $ Nd2 Tip c Tip
| otherwise = Left t
mx (Nd2 _ d _) = (d, Right Tip)
mx (Nd3 _ c _ f _) = (f, Left $ Nd2 Tip c Tip)
Tip vをNodeとして考えたときの「要素」が型vであるということを設定している。またvはEqクラスのインスタンスである必要がある。
検索
instance (Ord v, IsNode a, v ~ Elem a) => IsNode (Node v a) where
type Elem (Node v a) = v
mem v (Nd2 l d r)
| v < d = mem v l
| v == d = True
| otherwise = mem v r
mem v (Nd3 l c o f r)
| v < c = mem v l
| v == c = True
| v < f = mem v o
| v == f = True
| otherwise = mem v r
型Node v aの「要素」に型vを設定した。型v、型aはそれぞれOrdクラス、IsNodeクラスのインスタンスでなければならない。また型vと型Elem aとが同じ型である必要がある。これはもとの木とその枝となる木の持つ要素の型が同じである必要があるということだ。
追加
ins v t@(Nd2 l d r)
| v < d = Left $ case ins v l of
Left l' -> Nd2 l' d r
Right (k, a, m) -> Nd3 k a m d r
| v == d = Left t
| otherwise = Left $ case ins v r of
Left r' -> Nd2 l d r'
Right (q, g, s) -> Nd3 l d q g s
ins v t@(Nd3 l c o f r)
| v < c = case ins v l of
Left l' -> Left $ Nd3 l' c o f r
Right (k, a, m) -> Right (Nd2 k a m, c, Nd2 o f r)
| v == c = Left t
| v < f = case ins v o of
Left o' -> Left $ Nd3 l c o' f r
Right (n, d, p) -> Right (Nd2 l c n, d, Nd2 p f r)
| v == f = Left t
| otherwise = case ins v r of
Left r' -> Left $ Nd3 l c o f r'
Right (q, g, s) -> Right (Nd2 l c o, f, Nd2 q g s)
単相版と同じだ。
削除
del v (Nd2 l d r)
| v <= d = case if v < d then (d, del v l) else mx l of
(d', Left l') -> Left $ Nd2 l' d' r
(d', Right l') -> case r of
Nd2 q g s -> Right $ Nd3 l' d' q g s
Nd3 q g r' h s -> Left $
Nd2 (Nd2 l' d' q) g (Nd2 r' h s)
| otherwise = case del v r of
Left r' -> Left $ Nd2 l d r'
Right r' -> case l of
Nd2 k a m -> Right $ Nd3 k a m d r'
Nd3 k a l' b m -> Left $
Nd2 (Nd2 k a l') b (Nd2 m d r')
del v (Nd3 l c o f r)
| v <= c = Left $ case if v < c then (c, del v l) else mx l of
(c', Left l') -> Nd3 l' c' o f r
(c', Right l') -> case o of
Nd2 n d p -> Nd2 (Nd3 l' c' n d p) f r
Nd3 n d o' e p ->
Nd3 (Nd2 l' c' n) d (Nd2 o' e p) f r
| v <= f = Left $ case if v < f then (f, del v o) else mx o of
(f', Left o') -> Nd3 l c o' f' r
(f', Right o') -> case l of
Nd2 k a m -> Nd2 (Nd3 k a m c o') f' r
Nd3 k a l' b m ->
Nd3 (Nd2 k a l') b (Nd2 m c o') f r
| otherwise = Left $ case del v r of
Left r' -> Nd3 l c o f r'
Right r' -> case o of
Nd2 n d p -> Nd2 l c (Nd3 n d p f r')
Nd3 n d o' e p ->
Nd3 l c (Nd2 n d o') e (Nd2 p f r')
mx (Nd2 l d r) = case mx r of
(u, Left r') -> (u, Left $ Nd2 l d r')
(u, Right r') -> (u ,) $ case l of
Nd2 k a m -> Right $ Nd3 k a m d r'
Nd3 k a l' b m -> Left $ Nd2 (Nd2 k a l') b (Nd2 m d r')
mx (Nd3 l c o f r) = case mx r of
(u, Left r') -> (u, Left $ Nd3 l c o f r')
(u, Right r') -> (u ,) . Left $ case o of
Nd2 n d p -> Nd2 l c (Nd3 n d p f r')
Nd3 n d o' e p -> Nd3 l c (Nd2 n d o') e (Nd2 p f r')
単相版と同じだ。
Tree型に対する操作
member :: (Ord v, IsNode a, v ~ Elem a) => v -> Tree v a -> Bool
member v (Zero n) = mem v n
member v (Succ t) = member v t
insert :: (Ord v, IsNode a, v ~ Elem a) => v -> Tree v a -> Tree v a
insert v (Zero n) = case ins v n of
Left n' -> Zero n'
Right (l, d, r) -> Succ . Zero $ Nd2 l d r
insert v (Succ t) = Succ $ insert v t
delete :: (Ord v, IsNode a, v ~ Elem a) => v -> Tree v a -> Tree v a
delete v (Succ (Zero n)) = case del v n of
Left n' -> Succ $ Zero n'
Right n' -> Zero n'
delete v (Succ t) = Succ $ delete v t
delete _ t = t
型v、型aがそれぞれOrdクラス、IsNodeクラスのインスタンスである必要があるということと型vが型aの要素である必要があるという型制約がある。
時間効率の比較
手づくりの重み平衡木と比較する
比較対称として重み平衡木の説明のSetT.hsを使用する。
import Data.Time
import System.Random
import qualified SetT as T
import qualified SetB as B
main :: IO ()
main = do
time (nthT T.empty (randoms $ mkStdGen 8) 20000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 40000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 80000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 160000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 320000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 640000 :: Maybe Int)
putStrLn ""
time (nthB B.empty (randoms $ mkStdGen 8) 20000 :: Maybe Int)
time (nthB B.empty (randoms $ mkStdGen 8) 40000 :: Maybe Int)
time (nthB B.empty (randoms $ mkStdGen 8) 80000 :: Maybe Int)
time (nthB B.empty (randoms $ mkStdGen 8) 160000 :: Maybe Int)
time (nthB B.empty (randoms $ mkStdGen 8) 320000 :: Maybe Int)
time (nthB B.empty (randoms $ mkStdGen 8) 640000 :: Maybe Int)
time :: Show a => a -> IO ()
time x = do
t0 <- getCurrentTime
print x
t1 <- getCurrentTime
print $ t1 `diffUTCTime` t0
nthT :: Ord a => T.Set a -> [a] -> Int -> Maybe a
nthT s (x : xs) n
| x `T.member` s = nthT s xs n
| n < 1 = Just x
| otherwise = nthT (T.insert x s) xs (n - 1)
nthT _ _ _ = Nothing
nthB :: Ord a => B.Set a -> [a] -> Int -> Maybe a
nthB s (x : xs) n
| x `B.member` s = nthB s xs n
| n < 1 = Just x
| otherwise = nthB (B.insert x s) xs (n - 1)
nthB _ _ _ = Nothing
% ghc -Wall nth.hs
% ./nth
Just (-65105102)
0.142771s
Just 2091415055
0.309148s
Just (-37343952)
0.66792s
Just 921951543
1.442277s
Just 1766916110
3.161275s
Just (-1105960261)
6.872912s
Just (-65105102)
0.15643s
Just 2091415055
0.38101s
Just (-37343952)
0.865995s
Just 921951543
1.953758s
Just 1766916110
4.43734s
Just (-1105960261)
9.789042s
ランダムな挿入では重み平衡木のほうがいくぶん速い。ランダムな挿入では木のかたよりが発生しにくいため重み平衡木で木の回転が発生する頻度が低いためであると考えられる。木のかたよりがしばしば発生する例で試してみよう。main関数を変更する。
main :: IO ()
main = do
time (nthT T.empty [0 ..] 20000 :: Maybe Int)
time (nthT T.empty [0 ..] 40000 :: Maybe Int)
time (nthT T.empty [0 ..] 80000 :: Maybe Int)
time (nthT T.empty [0 ..] 160000 :: Maybe Int)
time (nthT T.empty [0 ..] 320000 :: Maybe Int)
time (nthT T.empty [0 ..] 640000 :: Maybe Int)
putStrLn ""
time (nthB B.empty [0 ..] 20000 :: Maybe Int)
time (nthB B.empty [0 ..] 40000 :: Maybe Int)
time (nthB B.empty [0 ..] 80000 :: Maybe Int)
time (nthB B.empty [0 ..] 160000 :: Maybe Int)
time (nthB B.empty [0 ..] 320000 :: Maybe Int)
time (nthB B.empty [0 ..] 640000 :: Maybe Int)
% ghc -Wall nth2.hs
% ./nth2
Just 20000
0.100906s
Just 40000
0.208186s
Just 80000
0.451062s
Just 160000
0.957839s
Just 320000
2.036245s
Just 640000
4.321803s
Just 20000
0.083354s
Just 40000
0.178033s
Just 80000
0.38154s
Just 160000
0.818599s
Just 320000
1.734653s
Just 640000
3.64391s
BB木による実装のほうが重み平衡木による実装より速い。
コード - 辞書
集合とほとんど同じだが鍵に対する値を置くスロットが追加される。
{-# LANGUAGE TupleSections, TypeFamilies #-}
module MapB (Map, empty, lookup, insert, delete) where
import Prelude hiding (lookup)
type Map k v = Tree k v (Tip k v)
data Tree k v a = Zero a | Succ (Tree k v (Node k v a)) deriving Show
data Node k v a = Nd2 a k v a | Nd3 a k v a k v a deriving Show
data Tip k v = Tip deriving Show
empty :: Tree k v (Tip k v)
empty = Zero Tip
{-
l d r
+-+-+ +-+-+
| a | | g |
k m q s
l d r
+---+---+ +---+---+
| a | b | | g | h |
k l' m q r' s
l c o f r
+-+-+ +-+-+ +-+-+
| a | | d | | g |
k m n p q s
l c o f r
+---+---+ +---+---+ +---+---+
| a | b | | d | e | | g | h |
k l' m n o' p q r' s
-}
class IsNode a where
type Key a
type Val a
lu :: Key a -> a -> Maybe (Val a)
ins :: Key a -> Val a -> a -> Either a (a, Key a, Val a, a)
del :: Key a -> Node (Key a) (Val a) a ->
Either (Node (Key a) (Val a) a) a
mx :: Node (Key a) (Val a) a ->
(Key a, Val a, Either (Node (Key a) (Val a) a) a)
instance Eq k => IsNode (Tip k v) where
type Key (Tip k v) = k
type Val (Tip k v) = v
lu _ _ = Nothing
ins k v _ = Right (Tip, k, v, Tip)
del k t@(Nd2 _ d _ _)
| k == d = Right Tip
| otherwise = Left t
del k t@(Nd3 _ c vc _ f vf _)
| k == c = Left $ Nd2 Tip f vf Tip
| k == f = Left $ Nd2 Tip c vc Tip
| otherwise = Left t
mx (Nd2 _ d vd _) = (d, vd, Right Tip)
mx (Nd3 _ c vc _ f vf _) = (f, vf, Left $ Nd2 Tip c vc Tip)
instance (Ord k, IsNode a, k ~ Key a, v ~ Val a) => IsNode (Node k v a) where
type Key (Node k v a) = k
type Val (Node k v a) = v
lu k (Nd2 l d vd r)
| k < d = lu k l
| k == d = Just vd
| otherwise = lu k r
lu k (Nd3 l c vc o f vf r)
| k < c = lu k l
| k == c = Just vc
| k < f = lu k o
| k == f = Just vf
| otherwise = lu k r
ins k v t@(Nd2 l d vd r)
| k < d = Left $ case ins k v l of
Left l' -> Nd2 l' d vd r
Right (k, a, va, m) -> Nd3 k a va m d vd r
| k == d = Left t
| otherwise = Left $ case ins k v r of
Left r' -> Nd2 l d vd r'
Right (q, g, vg, s) -> Nd3 l d vd q g vg s
ins k v t@(Nd3 l c vc o f vf r)
| k < c = case ins k v l of
Left l' -> Left $ Nd3 l' c vc o f vf r
Right (k, a, va, m) ->
Right (Nd2 k a va m, c, vc, Nd2 o f vf r)
| k == c = Left t
| k < f = case ins k v o of
Left o' -> Left $ Nd3 l c vc o' f vf r
Right (n, d, vd, p) ->
Right (Nd2 l c vc n, d, vd, Nd2 p f vf r)
| k == f = Left t
| otherwise = case ins k v r of
Left r' -> Left $ Nd3 l c vc o f vf r'
Right (q, g, vg, s) ->
Right (Nd2 l c vc o, f, vf, Nd2 q g vg s)
del k (Nd2 l d vd r)
| k <= d = case if k < d then (d, vd, del k l) else mx l of
(d', vd', Left l') -> Left $ Nd2 l' d' vd' r
(d', vd', Right l') -> case r of
Nd2 q g vg s -> Right $ Nd3 l' d' vd' q g vg s
Nd3 q g vg r' h vh s -> Left $ Nd2
(Nd2 l' d' vd' q)
g vg
(Nd2 r' h vh s)
| otherwise = case del k r of
Left r' -> Left $ Nd2 l d vd r'
Right r' -> case l of
Nd2 k a va m -> Right $ Nd3 k a va m d vd r'
Nd3 k a va l' b vb m -> Left $
Nd2 (Nd2 k a va l') b vb (Nd2 m d vd r')
del k (Nd3 l c vc o f vf r)
| k <= c = Left $ case if k < c then (c, vc, del k l) else mx l of
(c', vc', Left l') -> Nd3 l' c' vc' o f vf r
(c', vc', Right l') -> case o of
Nd2 n d vd p -> Nd2
(Nd3 l' c' vc' n d vd p)
f vf
r
Nd3 n d vd o' e ve p -> Nd3
(Nd2 l' c' vc' n)
d vd
(Nd2 o' e ve p) f vf r
| k <= f = Left $ case if k < f then (f, vf, del k o) else mx o of
(f', vf', Left o') -> Nd3 l c vc o' f' vf' r
(f', vf', Right o') -> case l of
Nd2 k a va m -> Nd2
(Nd3 k a va m c vc o')
f' vf'
r
Nd3 k a va l' b vb m -> Nd3
(Nd2 k a va l')
b vb
(Nd2 m c vc o')
f vf
r
| otherwise = Left $ case del k r of
Left r' -> Nd3 l c vc o f vf r'
Right r' -> case o of
Nd2 n d vd p -> Nd2
l
c vc
(Nd3 n d vd p f vf r')
Nd3 n d vd o' e ve p -> Nd3
l
c vc
(Nd2 n d vd o')
e ve
(Nd2 p f vf r')
mx (Nd2 l d vd r) = case mx r of
(u, v, Left r') -> (u, v, Left $ Nd2 l d vd r')
(u, v, Right r') -> (u , v,) $ case l of
Nd2 k a va m -> Right $ Nd3 k a va m d vd r'
Nd3 k a va l' b vb m -> Left $
Nd2 (Nd2 k a va l') b vb (Nd2 m d vd r')
mx (Nd3 l c vc o f vf r) = case mx r of
(u, v, Left r') -> (u, v, Left $ Nd3 l c vc o f vf r')
(u, v, Right r') -> (u, v,) . Left $ case o of
Nd2 n d vd p -> Nd2 l c vc (Nd3 n d vd p f vf r')
Nd3 n d vd o' e ve p ->
Nd3 l c vc (Nd2 n d vd o') e ve (Nd2 p f vf r')
lookup :: (Ord k, IsNode a, k ~ Key a, v ~ Val a) => k -> Tree k v a -> Maybe v
lookup k (Zero n) = lu k n
lookup k (Succ t) = lookup k t
insert :: (Ord k, IsNode a, k ~ Key a, v ~ Val a) =>
k -> v -> Tree k v a -> Tree k v a
insert k v (Zero n) = case ins k v n of
Left n' -> Zero n'
Right (l, d, vd, r) -> Succ . Zero $ Nd2 l d vd r
insert k v (Succ t) = Succ $ insert k v t
delete :: (Ord k, IsNode a, k ~ Key a, v ~ Val a) =>
k -> Tree k v a -> Tree k v a
delete k (Succ (Zero n)) = case del k n of
Left n' -> Succ $ Zero n'
Right n' -> Zero n'
delete k (Succ t) = Succ $ delete k t
delete _ t = t
まとめ
均衡のとれた木のほうが探索などの操作の効率が良い。2分木ですべての枝の高さが同じにすると正確に2^n-1個の要素しか格納できない。任意の個数の要素を格納するために2分岐のノードだけでなく3分岐のノードも許すことにする。探索木では値をノードに格納するほうがスマートだ。2分岐と3分岐のノードがあり値をノードに格納する木はオーダーを3にしたB木と同じものでありBB木と呼ばれる。
Haskellの型システムをうまく使うことで型レベルで木の高さがそろっていることが保証される木構造を作ることができる。この構造で木に含まれる要素に任意の型を使いたければTypeFamilies拡張が必要だ。
実際にBB木でSetを実装して重み平衡木で実装したSetと比較してみた。ランダムな挿入では重み平衡木版のほうが速度が出たが、木のかたよりが多発するような挿入のしかたではBB木のほうが速い。ただし、そもそも重み平衡木の「僕の実装」には無駄な処理がある。
BB木による集合や辞書の実装は型レベルで高さの均衡が保証されるという美しさがあり速度もそこそこ出るということだ。