状態変化なしに効率的な辞書を実装する重み平衡木
はじめに
キーを指定して値を検索したいことはよくある。このような操作のために作られたデータ構造を辞書や連想配列と呼ぶ。多くの言語では辞書としてハッシュテーブルを使う。ハッシュテーブルの時間効率は「いちおう」O(1)ということになっている。しかし、ハッシュテーブルは「状態変化」を前提としたデータ構造だ。ハッシュテーブルは挿入・削除の操作のたびに変化し続ける。
状態変化があるということはコードの実行順序によって値が変化する可能性があるということだ。状態変化による結果を完全に理解することは人間の得意とするところではない。すぐに人間の思考はごちゃごちゃになってしまう。そしてよく訓練されたHaskellerなら非本質的な状態変化を「美しくない」と感じるはずだ。
リストによる辞書
そうだリストを使おう。リストを使えば状態変化にわずらわされることはない。キーと値のタプルのリストにMapという別名をつけて辞書として使うことを考える。
type Map k a = [(k, a)]
検索、挿入、削除ができればいい。初期値として空の辞書も用意しよう。
empty :: Map k a
empty = []
-- lookup :: Eq k => k -> Map k a -> a
-- lookup = [Preludeにある]
insert :: k -> a -> Map k a -> Map k a
insert = curry (:)
delete :: Eq k => k -> Map k a -> Map k a
delete = filter . (. fst) . (/=)
検索用の関数lookupはPreludeに定義ずみなのでそれを使う。関数insertや関数deleteはポイントフリースタイルにしておいた。
これで辞書としてのひととおりの操作ができる。時間効率は検索がO(n)、挿入がO(1)、削除がO(n)となる。
O(n)だって!
O(n)となるのはリストの検索が線形探索となっているからだ。実世界で辞書を引くときに最初から順に単語を読んでいく人がいるだろうか。線形探索というのはそのくらいに非効率的な方法だ。
集合
ここで唐突に「集合」という言葉が出てきた。これから効率的な辞書を実装していくのだが本質的には同じでより単純な集合について考えていくことにする。集合というものは値がそれに含まれるかどうかを判定するものだ。辞書というものはキーに対応する値が存在するかどうかを判定し、存在したらその値を返すものだ。「対応する値」を無視するようにすれば辞書を集合として使うことができる。以下のような関係となるだろう。
type Set a = Map a ()
ユニット型は1種類の値しか持たない型である。つまり情報量は0だ。
集合のリストによる実装
リストによる集合の実装は以下のようになる。
module SetL (Set, empty, member, insert, delete) where
type Set a = [a]
empty :: Set a
empty = []
member :: Eq a => a -> Set a -> Bool
member = elem
insert :: a -> Set a -> Set a
insert = (:)
delete :: Eq a => a -> Set a -> Set a
delete = filter . (/=)
リストの重複を削除したインデクシング
実行効率について語っていくための例題を用意した。リストのインデクシングだ。たとえば文字のリスト"Hello, world!"の7番目は'w'である。それでは文字の重複を削除して考えるとどうだろうか(関数nubを使えばいいだろうというつっこみはここではなしにする)。2度目に出てくる'l'と'o'を無視するのでこの場合の7番目は'r'となる。これを求める関数を例題としよう。
上記の「リストによる集合」を利用して書いてみよう。
import qualified SetL as L
nthL :: Eq a => L.Set a -> [a] -> Int -> Maybe a
nthL s (x : xs) n
| x `L.member` s = nthL s xs n
| n < 1 = Just x
| otherwise = nthL (L.insert x s) xs (n - 1)
nthL _ _ _ = Nothing
試してみよう。
% ghci nth.hs
*Main> nthL L.empty "Hello, world!" 7
'r'
実行効率
L.memberはリストの要素を線形探索するのでO(n)だ。関数nthLは要素をひとつ走査するたびにL.memberをするので時間効率はO(n^2)となるはずだ。長いランダム列を使って処理にかかる時間を調べてみよう。まずは必要なモジュールを導入する。
import System.Random
import Data.Time
実行時間を求める関数を作成する。Haskellの遅延評価という性質をうまく利用した。引数となる値が未評価である必要がある。
time :: Show a => a -> IO ()
time = do
t0 <- getCurrentTime
print x
t1 <- getCurrentTime
print $ t1 `diffUTCTime` t0
時間計測用の関数mainを作成する。
main :: IO ()
main = do
time (nthL L.empty (randoms $ mkStdGen 8) 10000 :: Maybe Int)
time (nthL L.empty (randoms $ mkStdGen 8) 20000 :: Maybe Int)
time (nthL L.empty (randoms $ mkStdGen 8) 40000 :: Maybe Int)
time (nthL L.empty (randoms $ mkStdGen 8) 80000 :: Maybe Int)
コンパイルして実行してみよう。
% ghc -Wall nth.hs
% ./nth
Just (-1935099869)
0.66362s
Just (-65105102)
2.589716s
Just 2091415055
10.228787s
Just (-37343952)
40.843141s
僕の環境では以上のようになった。nが2倍で時間が4倍となっている。O(n^2)という予想と矛盾しない。
二分探索木
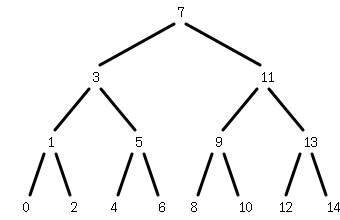
リストによる集合の検索がO(n)かかってしまうのは線形探索が行われているためだ。たとえば0から14までの並びではじめから順に6に到達するには0から6までの7つの数字を調べる必要がある。しかし以下のような二分木に数字が保存されていれば、6に到達するには、7より小さい、3より大きい、5より大きい、6と等しい、のように4回の比較ですむ。
このように調べる範囲を半分ずつにせばめていくような探索のしかたを二分探索と呼ぶ。うえの例ではそんなに大きな違いは感じないかもしれない。しかし、要素の数が増えると線形探索と二分探索の効率の差は顕著になる。
要素の数が1000倍になれば線形探索では時間が1000倍かかるのに対し二分探索では10倍ですむ。要素の数が1000000倍になれば線形探索では1000000倍の時間がかかるが二分探索では20倍ですむ。
木の均衡
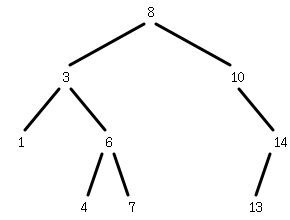
要素の数は2のベキ乗であるとは限らないのでつねに完全な均衡を保つことは不可能だ。実際の二分探索木は以下のような形となる。
それぞれのノードは子を持たないか左右のどちらかまたは両方の子を持つかである。上図の木は比較的均衡のとれた木だ。たとえばこのような木は「8, 3, 10, 6, 1, 14, 13, 7, 4」のような順に要素を挿入していくとできる。たとえば、小さい順に値を挿入していったらどうなるだろうか。「1, 3, 4, 6, 7, 8, 10, 13, 14」のように要素を挿入していくと根が1となりどのノードも右の子しか持たないかたよった木となってしまう。これは本質的にはリストと同じことでこの木に対する検索は線形探索と同じことになる。
つまり、効率的な探索を可能にするためには木の均衡が重要となってくる。
木の回転により均衡を保つ
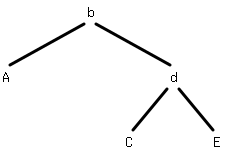
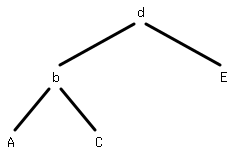
「木を左回転する」とは以下の
ひとつめの木をふたつめの木に変換することを言う。dを持ってうえに引っぱり、Cからdにのびる線をbにつけかえてやる。こうすることで右を軽くして左を重くすることができる。右回転はこれを逆にすればいい。
木に含まれる要素の数を木の「重さ」と表現する。どこをとっても左右の木の「重さ」の比が3以下であるようにしたい。右が左の3倍を越えたら左回転し左が右の3倍を越えたら右回転すれば良いように思われる。
二重回転
上記のような単純な回転ではうまくいかないことがある。上図のCの位置にある木が重かったときもともとは右が重すぎるが、左回転では左が重くなりすぎるということがありえる。これを解決するためにはCの位置にある木を軽くしてやればいい。つまり、全体を左回転するまえにd以下の木を右回転してやればいい。これを左二重回転と呼ぼう。
左回転するときには右の子の右の子を、右回転するときには左の子の左の子をそれぞれ外側の子と呼び、それぞれ右の子の左の子と左の子の右の子を内側の子と呼ぼう。このとき外側の子よりも内側の子のほうが2倍以上重かったときに二重回転が必要であることが知られている。
回転のまとめ
- 左右の子の重さの比が3を越えたときに回転が必要になる
- 外側の子よりも内側の子のほうが2倍以上重いときには二重回転が必要になる
このように木の重さを比較して回転のしかたを決めることで均衡を保つ木を重み平衡木(weight balanced tree)と呼ぶ。
重み平衡木による集合の実装
モジュール宣言など
module SetT (Set, empty, member, insert, delete) where
import Control.Arrow (second)
モジュールArrowのsecondをタプルの二要素目に関数を適用する関数として利用する。
型とスマート構築子、スマート取得子
data Set a = Empty | Bin {
_weight :: Int,
_value :: a,
left :: Set a,
right :: Set a
} deriving Show
empty :: Set a
empty = Empty
weight :: Set a -> Int
weight Empty = 0
weight t = _weight t
bin :: a -> Set a -> Set a -> Set a
bin x l r = Bin (weight l + weight r + 1) x l r
emptyは空集合を意味する。weightはEmptyにも対応した重さの取得子だ。binは重さを自動計算してくれる構築子である。
値の検索
member :: Ord a => a -> a -> Set a -> Bool
member x (Bin _ x0 l r)
| x < x0 = member x l
| x > x0 = member x r
| otherwise = True
member _ _ = False
調べる値が現在のノードの値よりも小さければ左を大きければ右を再帰的に調べていく。
定数の定義
delta, ratio :: Int
delta = 3
ratio = 2
左右の木の重さの比がdeltaを越えたら回転させる。内側の木の重さが外側の木の重さのratio倍以上であれば二重回転とする。
均衡を回復する関数
balance :: Set a -> Set a
balance t@(Bin _ x l r)
| weight l + weight r < 2 = t
| weight r > delta * weight l =
if weight (left r) >= ratio * weight (right r)
then rotateL $ bin x l (rotateR r)
else rotateL t
| weight l > delta * weight r =
if weight (right l) >= ratio * weight (left l)
then rotateR $ bin x (rotateL l) r
else rotateR t
| otherwise = t
それぞれの場合について回転をするかどうかやどの回転をするかをふるいわけしている。実際の回転は関数rotateL, rotateRによって行われる。
rotateL, rotateR :: Set a -> Set a
rotateL (Bin _ x lx (Bin _ y ly ry)) = bin y (bin x lx ly) ry
rotateL _ = error "rotateL: can't rotate"
rotateR (Bin _ x (Bin _ y ly ry) rx) = bin y ly (bin x ry rx)
rotateR _ = error "rotateR: can't rotate"
値の挿入
insert :: Ord a => a -> Set a -> Set a
insert x Empty = bin x Empty Empty
insert x t@(Bin _ x0 l r)
| x < x0 = balance $ bin x0 (insert x l) r
| x > x0 = balance $ bin x0 l (insert x r)
| otherwise = t
xがノードの値よりも小さければ左に大きければ右に値を追加する。値を追加したあとには関数balanceで均衡を回復させる。
値の削除
delete :: Ord a => a -> Set a -> Set a
delete _ Empty = Empty
delete x (Bin _ x0 l r)
| x < x0 = balance $ bin x0 (delete x l) r
| x > x0 = balance $ bin x0 l (delete x r)
| otherwise = glue l r
削除する値がノードの値よりも小さければ左から大きければ右から値を削除する。削除する値がノードの値と等しければこのノードを削除する必要があるのでこのノードを除いて左右の木を融合させる。融合には以下で定義する関数glueを使う。
glue :: Set a -> Set a -> Set a
glue Empty r = r
glue l Empty = l
glue l r
| weight l > weight r = let (m, l') = popMax l in balance $ bin m l' r
| otherwise = let (m, r') = popMin r in balance $ bin m l r'
片方の木が空ならば残りの木が結果となる。そうでないなら、大きいほうの木のはじっこをとりだしてそれを根とした新しい木を作る。
popMin, popMax :: Set -> (a, Set a)
popMin (Bin _ x Empty r) = (x, r)
popMin (Bin _ x l r) = (balance . flip (bin x) r) `second` popMin l
popMin _ = error "popMin: Empty"
popMax (Bin _ x l Empty) = (x, l)
popMax (Bin _ x l r) = (balance . bin x l) `second` popMax r
popMax _ = error "popMax: Empty"
関数popMinは左の子が空になるまで木をたどっていきそこの値と右の木をとりだす。もどりながら木を再構築していく。関数popMaxは左右を逆にして同じことをする関数だ。
実行効率のチェック
木による集合モジュールをnth.hsに導入する。
import qualified SetT as T
nthTを定義する。nthLとほとんど同じだ。
nthT :: Ord a => T.Set a -> [a] -> Int -> Maybe a
nthT s (x : xs) n
| x `T.member` s = nthT s xs n
| n < 1 = Just x
| otherwise = nth (T.insert x s) xs (n - 1)
nthT _ _ _ = Nothing
main関数に木を使った版のテストを追加する。
main :: IO ()
main = do
...
time (nthT T.empty (randoms $ mkStdGen 8) 10000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 20000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 40000 :: Maybe Int)
time (nthT T.empty (randoms $ mkStdGen 8) 80000 :: Maybe Int)
コンパイルして実行する。
% ghc -Wall nth.hs
% ./nth
...
Just (-1935099869)
0.061622s
Just (-65105102)
0.142313s
Just 2091415055
0.300382s
Just (-37343952)
0.662469s
40000番目を求めるテストではリストを使ったときの10秒と比較して0.3秒と30倍の効率だ。80000番目を求めるテストでは40秒と0.66秒で60倍の効率となっている。
重み平衡木による辞書の実装
集合とほぼ同じだ。キーに対する「値」をいれるスロットが追加される。
module MapT (Map, empty, lookup, insert, delete) where
import Prelude hiding (lookup)
import Control.Arrow (second)
data Map k a = Empty | Bin {
_weight :: Int,
_key :: k,
_value :: a,
left :: Map k a,
right :: Map k a
} deriving Show
empty :: Map k a
empty = Empty
weight :: Map k a -> Int
weight Empty = 0
weight t = _weight t
bin :: k -> a -> Map k a -> Map k a -> Map k a
bin k x l r = Bin (weight l + weight r + 1) k x l r
lookup :: Ord k => k -> Map k a -> Maybe a
lookup k (Bin _ k0 x l r)
| k < k0 = lookup k l
| k > k0 = lookup k r
| otherwise = Just x
lookup _ _ = Nothing
delta, ratio :: Int
delta = 3
ratio = 2
balance :: Map k a -> Map k a
balance Empty = Empty
balance t@(Bin _ k x l r)
| weight l + weight r < 2 = t
| weight r > delta * weight l =
if weight (left r) >= ratio * weight (right r)
then rotateL $ bin k x l (rotateR r)
else rotateL t
| weight l > delta * weight r =
if weight (right l) >= ratio * weight (left l)
then rotateR $ bin k x (rotateL l) r
then rotateR $ bin k x (rotateL l) r
else rotateR t
| otherwise = t
rotateL, rotateR :: Map k a -> Map k a
rotateL (Bin _ j x lx (Bin _ k y ly ry)) = bin k y (bin j x lx ly) ry
rotateL _ = error "rotateL: can't rotate"
rotateR (Bin _ j x (Bin _ k y ly ry) rx) = bin k y ly (bin j x ry rx)
rotateR _ = error "rotateR: can't rotate"
insert :: Ord k => k -> a -> Map k a -> Map k a
insert k x Empty = bin k x Empty Empty
insert k x t@(Bin _ k0 x0 l r)
| k < k0 = balance $ bin k0 x0 (insert k x l) r
| k > k0 = balance $ bin k0 x0 l (insert k x r)
| otherwise = t
delete :: Ord k => k -> Map k a -> Map k a
delete _ Empty = Empty
delete k (Bin _ k0 x0 l r)
| k < k0 = balance $ bin k0 x0 (delete k l) r
| k > k0 = balance $ bin k0 x0 l (delete k r)
| otherwise = glue l r
glue :: Map k a -> Map k a -> Map k a
glue Empty r = r
glue l Empty = l
glue l r
| weight l > weight r =
let ((k, x), l') = popMax l in balance $ bin k x l' r
| otherwise = let ((k, x), r') = popMin r in balance $ bin k x l r'
popMin, popMax :: Map k a -> ((k, a), Map k a)
popMin (Bin _ k x Empty r) = ((k, x), r)
popMin (Bin _ k x l r) = (balance . flip (bin k x) r) `second` popMin l
popMin _ = error "popMin: Empty"
popMax (Bin _ k x l Empty) = ((k, x), l)
popMax (Bin _ k x l r) = (balance . bin k x l) `second` popMax r
popMax _ = error "popMax: Empty"
標準的なライブラリ
Haskellの標準的なモジュールであるData.SetやData.Mapのデータ型Set, Mapは本質的にはここで学んだのと同様のデータ構造である。
まとめ
辞書をリストで定義すると線形探索となり時間効率がO(n)となる。ハッシュを使うと「いちおう」O(1)となるが状態変化を多用したアルゴリズムはコードが複雑になったときにバグを生む。また美しくない。重み平衡木を使うことでO(log n)で各操作が可能な状態変化を必要としない辞書を作成することができる。