Integral Neural Networks (Huaway, CVPR2023 award candidate)
お久しぶりです。Yosematです。CVPR2023に現地で参加して参りました。
本日は中でも今後のComputer Vision領域にBreak Thoroughをもたらしそうな論文Integral Neural Networksを紹介します。
忙しい人向け
- Neural Networkのベクトル同士の内積を関数同士の内積(積分)に拡張した
- Conv2DレイヤーだけでなくLinearレイヤーも可変長の入力を受け付けられるようになった
- Conv2Dレイヤーでは画像サイズが変わっても性能が落ちなくなった
- 離散表現の既存手法と比べて性能は同等以上だった
Neural Network = 行列の掛け算 = ベクトルの内積(の集まり)
たとえば普通のDenseLayerの計算はBiasを無視すれば重み行列$W \in \mathbb{R} ^ {M \times N}$と入力ベクトル$x \in \mathbb{R} ^ N$を用いて次のような計算になります。
$$
F(x) = Wx
$$
$i$番目の要素に絞るとこれは明らかに重み行列$W$の行ベクトルと$x$との内積です。
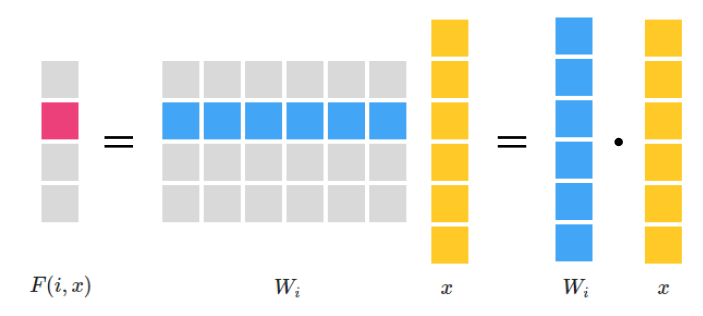
$$
F_O(i, x) = {W_i}^Tx = W_i \cdot x
$$
ベクトルの内積≒関数の内積
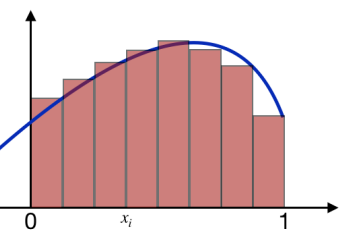
ベクトルの内積とは、関数の内積を離散化近似したものといえます。
関数の内積
定義域を$[0, 1]$としておきましょう。
関数$f$と関数$g$の内積は積分によって
$$
f \cdot g = \int_0^1 f(x) g(x) dx
$$
とかけます。
$$
f \cdot g = \int_0^1 f(x) g(x) dx = \lim_{n \rightarrow \infty}\sum_{i=1}^n f\left(\frac{i}{n}\right) g\left( \frac{i}{n} \right) \frac{1}{n}
$$
とかけましたね。※$h(x) = f(x)g(x)$と解釈するとわかりやすいかもしれません。
この考察からベクトルの内積は関数の内積を離散近似したものだととらえることができます。
Neural Network = ベクトルの内積(の集まり)≒関数の内積(の集まり)
重み行列の行ベクトル$W_i$と入力ベクトル$x$を関数に置き換えることはできるでしょうか。
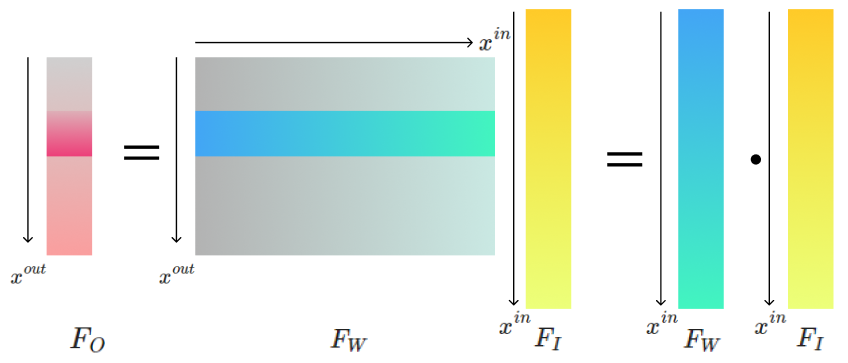
論文では行ベクトル$W_i$を関数$F_W$, 入力$x$を関数$F_I$と近似することで
$$
F_O(x^{out}) = F_W \cdot F_I = \int_0^1 F_W(\lambda, x^{out}, x^{in})F_I(x^{in})dx^{in}
$$
と近似することを提案しています。$\lambda$が学習パラメータ, $x^{out}$が出力の位置(本記事の重み行列の行インデックス$i$に対応), $x^{in}$が入力の位置(列インデックス$j$に対応)に対応します。
これによってニューラルネットワークの重みを連続関数で書き直すことができました。
好きな解像度で離散化できる

離散的な重み行列から連続的な関数に乗り換えたことのメリットは好きな解像度で離散化できることです。
これまでは重み行列$W$を$4 \times 6$で近似してしまったら最後、6次元のベクトルしか受け付けることはできませんでした。
Integral Neural Networksの登場によって任意の大きさのベクトルを入力に取ることのできるDNNが爆誕したのです。
連続的な重み表現
- $F_W(\lambda, x^{out}, x^{in})$の具体的な式を決定すること
- コンピュータで積分はできないし入力も連続関数じゃなくてベクトルであること
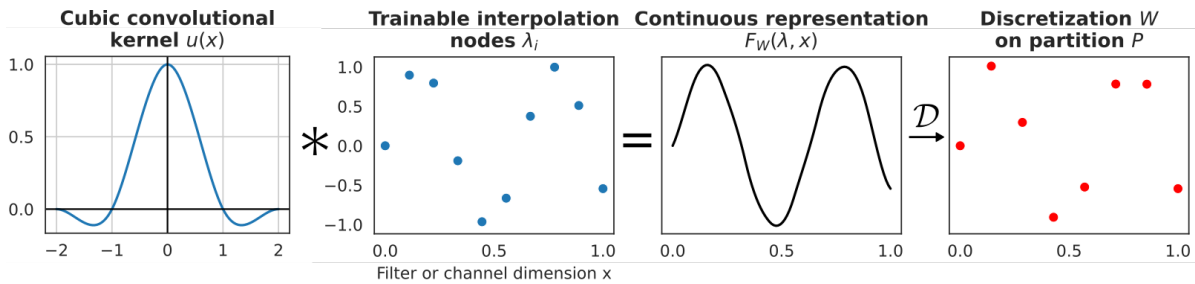
これらに対処するために論文では区間$[0, 1)$を$m$分割し各点の値をパラメータ$\lambda_i, i \in \mathbb{N}_m$で表現することを提案します。これだと列数$M$の離散行列を作ることと一緒になってしまうのでこの$m$個の点をCubic Interpolationします。
このInterpolationされた連続関数は推論時には再度入力の次元にあわせて離散化します。これにより既存のDeep Learning Frameworkを活用しながらも入力次元に囚われないDNNを開発することができました。
$$
F_W(\lambda, x^{out}, x^{in}) = \sum_{i, j} \lambda_{ij}u(x^{out}m^{out} - i)u(x^{in}m^{in} - j)
$$
もちろんこの議論は1次元入力のDenseLayerからConv2Dに拡張することができます。
結果
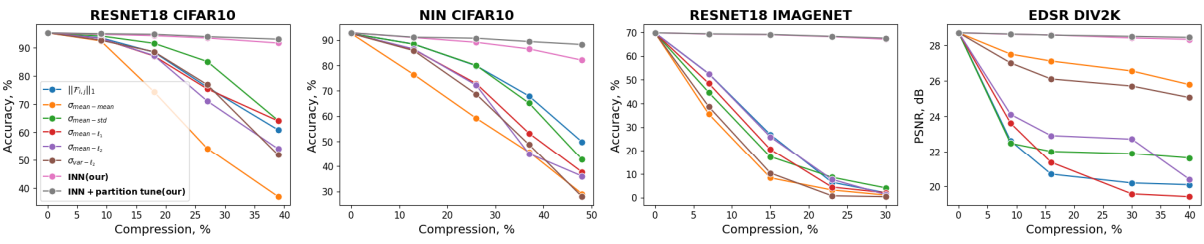
性能は落ちない
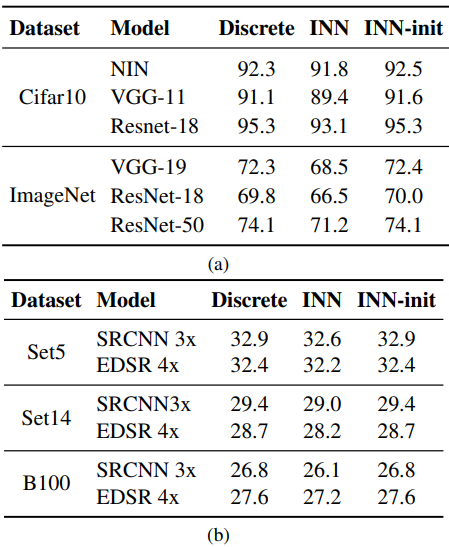
連続化によって任意の入力を受け付けることができるようになりましたが、その性能は既存のベンチマークでも落ちていません。上の表ではINN-initに注目してください。Integral Neuralnetworkは柔軟性を性能を損ねることなく獲得していることがわかります。
入力サイズがかわっても性能は落ちない
ResNetなどのConvolution系モデルは入力サイズが変わっても推論すること自体はできました。しかしResNetの入力サイズをかえると性能がガタ落ちします。
しかしIntegral Neural Networksは入力サイズがかわっても性能がほとんど落ちませんでした。
まとめ
Integral Neural Networksの導入によってComputer Visionの長年の課題が1つ解決されました。もうこれからはImageNetのPretrainedModelがどの解像度の画像で学習されたものなのかを気にする必要はありません。残念ながらCVPRのBest Paperは獲得できなかったもののCV研究の1つのBreak throughと受け止めております。
今後も深層学習に関する知見を共有しますのでいいねとフォローをいただけますと幸いです。Yosematでした。