行列の積と転置
準備のために行列の積と転置について説明します。
行列Aのサイズが(N,M)、行列Bのサイズが(M,L)とすると、行列C=ABの要素は以下のようになります。行列Aの列の数(横のサイズ)と行列Bの行の数(縦のサイズ)は一致させる必要があります。
c_{ij}=\sum_{k=1}^M a_{ik}b_{kj}
Aの転置行列は以下のようになります。(右が要素)
A: a_{ij} \; \rightarrow \; A^T: a_{ji}
転置行列と通常の行列の積は以下のようになります。添字の位置に注目して下さい。
C=A^T B \; \rightarrow \; c_{ij}=\sum_{k=1}^M a_{ki}b_{kj} \\
C=A B^T \; \rightarrow \; c_{ij}=\sum_{k=1}^M a_{ik}b_{jk}
順方向の計算
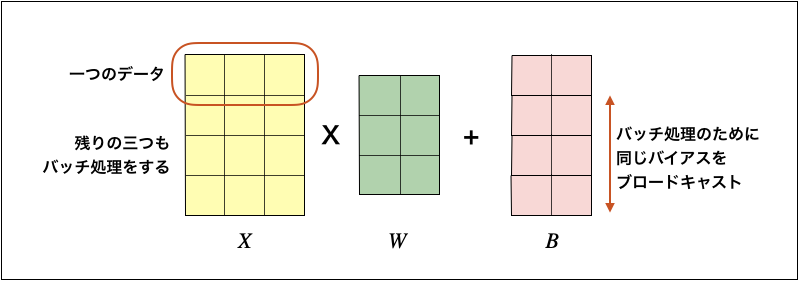
Affineレイヤの順方向の計算では、入力Xと重みWの行列の積を計算して、バイアスBを加算します。入力Xは以下のようにバッチ処理を行うものとします。
数式で書くと以下のようになります。バイアスBはXWの各行に加算するので添字にiはありません。
Y = XW + B : y_{ij} = \sum_k x_{ik}w_{kj}+b_j
Pythonで書くと下記のようになります。bは縦方向にブロードキャストします。本書のコードと説明のために少し変えています。
class Affine
def __init__(self, W, b):
self.W = W # サイズは(入力Xの要素数,次レイヤの入力の要素数)
self.b = b # サイズは(1,次レイヤの入力の要素数)
self.x = None
def forward(self, x):
self.x = x
out = np.dot(self.x, self.W) + self.b # bはブロードキャスト
return out # サイズは(データ数,次レイヤの入力の要素数)
逆方向の計算
行列の積について、出力Yと損失Lの微分であるdL/dyと、Yと(X,W)の関係式から、dL/dXとdL/dWを計算します。
以下のAffine変換の数式について、
y_{kl} = \sum_j x_{kj}w_{jl} + b_l
x, wで偏微分を計算すると、
\frac{\partial y_{kl}}{\partial x_{kj}} = w_{jl}, \;
\frac{\partial y_{kl}}{\partial w_{jl}} = x_{kj}
以下のクロネッカーのデルタを使って、
\delta_{ij} = \begin{cases} 1 & (i=j)\\ 0 & (i \ne j)\end{cases}
以下のように書き換えられます。
\frac{\partial y_{kl}}{\partial x_{ij}}
= \delta_{ik} \frac{\partial y_{il}}{\partial x_{ij}}
= \delta_{ik} w_{jl}, \;
\frac{\partial y_{kl}}{\partial w_{ij}}
= \delta_{jl} \frac{\partial y_{kj}}{\partial w_{ij}}
= \delta_{jl} x_{ki}
この関係を使って、dY/dXとdY/dWを計算します。
\frac{\partial L}{\partial x_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}}
\frac{\partial y_{kl}}{\partial x_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}} \delta_{ik} w_{jl}
= \sum_l \frac{\partial L}{\partial y_{il}} w_{jl} \\
\frac{\partial L}{\partial w_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}}
\frac{\partial y_{kl}}{\partial w_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}} \delta_{jl} x_{ki}
= \sum_k \frac{\partial L}{\partial y_{kj}} x_{ki}
これを行列を使って書き直すと以下になります。
\frac{\partial L}{\partial X} = \frac{\partial L}{\partial Y} W^T, \;
\frac{\partial L}{\partial W} = X^T \frac{\partial L}{\partial Y}
バイアスBについては以下の記事に書いた通り、
[ゼロから作るDeep Learning 〜誤差逆伝播法の概要〜]
(https://qiita.com/Yoko303/items/b67ea27ae221fb5386d1)
以下のようになります。
\frac{\partial L}{\partial b_l}
= \sum_{k} \frac{\partial L}{\partial y_{kl}}
以上をまとめてPythonで書くと以下になります。
class Affine
def backward(self, dout):
dx = np.dot(dout, self.W.T)
dW = np.dot(self.x.T, dout)
db = np.sum(dout, axis=0)
return dx, dw, db