はじめに
「ゼロから作るDeep Learning」を読了しました。理解に時間がかかった部分について、自分なりの理解を書いていきます。まずは誤差逆伝播法について書きます。
誤差逆伝播法の考え方
ニューラルネットワークは入力Xに対して、重みW、バイアスB等のパラメータを使った計算を繰り返して出力を得て、その出力により推論する手法です。ニューラルネットワークの学習の際には、その出力と教師データの差である損失Lを最小にするための最適なパラメータを探します。誤差逆伝播法は最適なパラメータを探すために使われます。
例えば、重みWを最適化するために、
W = W - \alpha \frac{\partial L}{\partial W}
として徐々にWを更新して探します。勾配降下法(=gradient descent method)と言います。αの設定方法はSGD, Adamなどがありますが、この記事では主にdL/dWの計算方法について説明します。
微分の計算方法
前述したように以降はdL/dW、つまり各入力パラメータの変化に対する損失Lの変化を計算する方法について説明していきます。
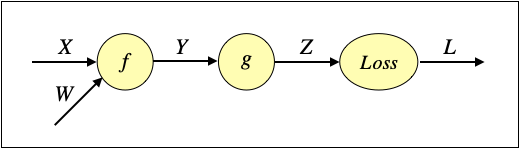
例として、下記のネットワークについて考えます。
入力X、重みW、中間値Y、Zはいずれも行列、損失Lはスカラーとします。関数fとgは行列を行列に変換する関数です。
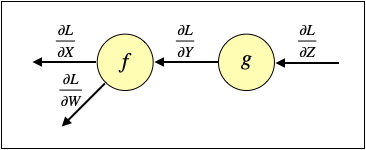
このネットワークで下記のように出力から逆にたどることでdL/dWを計算します。
ここで、dL/dZはZと、dL/dYはYと、dL/dXはXと、dL/dWはWと同じサイズであることに注意して下さい。
行列Zの要素を、
z_{ij}
とします。Y, Wも同様です。
dL/dZの要素は、
\frac{\partial L}{\partial z_{ij}}
となります。
Yの一要素が変化した時にZの全要素に影響が及ぶと仮定すると、dL/dYはZの全微分を計算することにより、
\frac{\partial L}{\partial y_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial z_{kl}}
\frac{\partial z_{kl}}{\partial y_{ij}}
となります。dL/dzは前述の計算により、dz/dyは関数gの偏微分により計算できます。
dL/dWの要素も同様に、
\frac{\partial L}{\partial w_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}}
\frac{\partial y_{kl}}{\partial w_{ij}}
となります。dL/dyは前述の計算により、dy/dwは関数fの偏微分により計算できます。
関数が各要素ごとの対応となる場合
関数gの入出力が同じサイズであり、且つ各要素ごとに同じ計算をする場合を考えます。
z_{ij}=g(y_{ij})
この時、以下が成立します。
\frac{\partial z_{kl}}{\partial y_{ij}}=0 \;\;
if \; k \neq i \; or \; l \neq j
この時、先述したdL/dyは、以下のようになります。
\frac{\partial L}{\partial y_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial z_{kl}}
\frac{\partial z_{kl}}{\partial y_{ij}}
= \frac{\partial L}{\partial z_{ij}}
\frac{\partial z_{ij}}{\partial y_{ij}}
= \frac{\partial L}{\partial z_{ij}} g^,(y_{ij})
この性質を使うと、各要素ごとに同じ計算をする関数に対して、簡単に微分を計算できます。
要素ごとの掛け算は、z=xyをそれぞれx,yで微分すると、以下になります。
\frac{\partial z_{ij}}{\partial x_{ij}} = y_{ij}
,\; \frac{\partial z_{ij}}{\partial y_{ij}} = x_{ij}
\; \rightarrow \;
\frac{\partial L}{\partial x_{ij}}
= \frac{\partial L}{\partial z_{ij}} y_{ij}
,\; \frac{\partial L}{\partial y_{ij}}
= \frac{\partial L}{\partial z_{ij}} x_{ij}
要素ごとの足し算は、z=x+yをそれぞれx,yで微分すると、以下になります。
\frac{\partial z_{ij}}{\partial x_{ij}} = 1
,\; \frac{\partial z_{ij}}{\partial y_{ij}} = 1
\; \rightarrow \;
\frac{\partial L}{\partial x_{ij}}
= \frac{\partial L}{\partial y_{ij}}
= \frac{\partial L}{\partial z_{ij}}
Pythonで書くと以下のようになります。説明に不要な部分は少し省略しています。基本的に順伝播(forward)の計算をしてから、逆伝播(backward)の計算をするので、順伝播の計算をした時の中間値を保存しておいて、逆伝播の計算をする時に利用します。
class MulLayer: # 乗算
def forward(self, x, y):
self.x = x # backwardの計算のため一時的に保存
self.y = y # backwardの計算のため一時的に保存
out = x * y
return out
def backward(self, dout):
dx = dout * self.y
dy = dout * self.x
return dx, dy
class AddLayer: # 加算
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout
dy = dout
return dx, dy
分岐する場合
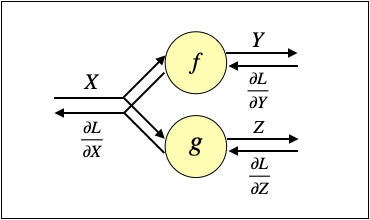
以下のように分岐する場合を考えます。
この時は、Xの一要素の変化が、YとZの全要素に影響を及ぼすと考えて、下記のように合計すれば良いです。
\frac{\partial L}{\partial x_{ij}}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}}
\frac{\partial y_{kl}}{\partial x_{ij}}
+ \sum_{k,l} \frac{\partial L}{\partial z_{kl}}
\frac{\partial z_{kl}}{\partial x_{ij}}
分岐の一例として、以下の数式のように同じバイアスBを分岐させて、各行に加算することを考えます。
y_{ij} = x_{ij} + b_j
Pythonで書くと以下のようにブロードキャストを使います。
def forward(x, b):
out = x + b # xのサイズは(N,M)、bのサイズは(1,M)
return out
dL/dBを計算する時はBの一要素の変化がYの全要素に影響を及ぼすと考えます。
\frac{\partial L}{\partial b_j}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}}
\frac{\partial y_{kl}}{\partial b_j}
= \sum_{k,l} \frac{\partial L}{\partial y_{kl}}
\delta_{jl} \frac{\partial y_{kj}}{\partial b_j}
= \sum_{k} \frac{\partial L}{\partial y_{kj}}
上記の三番目から四番目の式変形の時に以下の偏微分の式とクロネッカーのデルタと偏微分の式を使っています。
\frac{\partial y_{kj}}{\partial b_j} = 1, \;
\delta_{ij} = \begin{cases} 1 & (i=j)\\ 0 & (i \ne j)\end{cases}
Pythonで書くと以下のようになります。
def backward(dout):
db = np.sum(dout, axis=0) # 縦方向の合計
return db
順伝播の時に縦方向に分岐したので、逆伝播の時は縦方向の合計を取ります。
まとめ
上記のことをまとめると以下のようになります。
- 損失Lと入力Xの微分は、損失Lと入力Xの各要素の偏微分を行列として示す
- そのため入力Xと同じサイズになり勾配降下法を使える
- 損失Lと入力Xの各要素の偏微分は、損失Lと出力Yの各要素の偏微分及び入出力の関係性から計算する
- まずは入力Xの一要素の変化が出力Yの全要素に影響を及ぼすと仮定して全微分を計算し、その後係数が0になる条件により式を簡略化して、損失Lと入力Xの微分を計算する