レイマーチングでクリスマスツリーを作る方法を解説してみる

はじめに

シェーダ初心者です。
アドベントカレンダーなので何かクリスマスっぽい絵をレイマーチングで作りたかったのですが、
0から作る能力と時間がなかったのでshadertoyに上がっている素晴らしい作品を解説してみます。

今回解説するのがこちら

レイマーチング周りのコードを理解する

GLSLは下から読んだ方が理解しやすいのでまずはmainImage関数内から読んでいきましょう。

mainImage

void mainImage( out vec4 fragColor, in vec2 fragCoord ) {
    vec2 q = fragCoord.xy/iResolution.xy;
    vec2 p = -1.0+2.0*q;
    p.x *= iResolution.x/iResolution.y;

    float ang = 0.1*(40.0 + iTime);
    vec3 camPos = vec3(CAM_DIST*cos(ang), CAM_H, CAM_DIST*sin(ang));
    vec3 rayDir = getRayDir(normalize(LOOK_AT - camPos), p);
    vec3 color = render(camPos, rayDir);
    fragColor=vec4(color, 1.0);
}

この辺はお作法的な座標の正規化ですね。

vec2 q = fragCoord.xy/iResolution.xy;
vec2 p = -1.0+2.0*q;
p.x *= iResolution.x/iResolution.y;

qは0.0 ~ 1.0の範囲を取るので2倍にして-1.0することで-1.0 ~ 1.0の範囲に変換しています。
p.xは横のアスペクト比を固定するために画面の横幅を縦幅で割って比率をかけています。

こちらがレイマーチングの起点となる道具を揃えている部分です。

float ang = 0.1*(40.0 + iTime);
vec3 camPos = vec3(CAM_DIST*cos(ang), CAM_H, CAM_DIST*sin(ang));
vec3 rayDir = getRayDir(normalize(LOOK_AT - camPos), p);
vec3 color = render(camPos, rayDir);
fragColor=vec4(color, 1.0);

angはカメラアングルに利用する値で時間経過とともに値が変動するようになっています。
camPosは3次元ベクトルでx,y,z値をそれぞれ指定しています。
unityでカメラを触る時のように各矢印の方向を指定している形です。

今回の場合だとx軸とz軸にangを入れているのでクリスマスツリーの周辺をぐるぐる回るようになります。

rayDirは光の向きを表しています。
レイマーチングはカメラの位置とレイの向きが必要になるのでこの二つを準備しています。
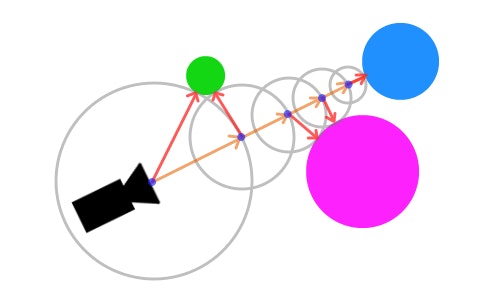
詳細はdoxasさんの記事を見るのが良いと思います。

※記事内で説明に利用されている画像。薄いオレンジの線がレイに当たる

getRayDir

vec3 getRayDir(vec3 viewDir, vec2 pixelPos) {
    vec3 camRight = normalize(cross(viewDir, vec3(0.0, 1.0, 0.0)));
    vec3 camUp = normalize(cross(camRight, viewDir));
    return normalize(pixelPos.x*camRight + pixelPos.y*camUp + CAM_FOV_FACTOR*viewDir);
}

rayの向きを計算しています。
こちらはcross（外積）の計算を行っています。

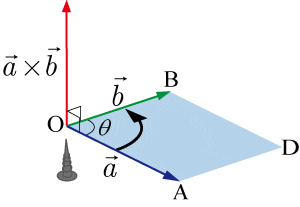
外積については下記の金沢工業大学の記事と掲載されている図がわかりやすいかと思います。

二つのベクトルがなす平行四辺形に垂直なベクトルを求めることができます。

viewDirはカメラの見ている方向のベクトルです。
原点からyを1.0だけずらした点(オブジェクトの中心にしたい点)とviewDirとの外積からカメラの右方向に伸びるベクトルを求められます。
その後カメラの右方向に伸びるベクトル(camRight)とviewDirの外積をとることでカメラの上方向のベクトルがわかります。
この二つがわかると、3次元ベクトルrayDirのx方向、y方向の値がわかります。
z方向に関してはcamRightとcamUp双方に対して垂直なviewDirがあるのでこちらと、定数で視野角を定義したCAM_FOV_FACTORを掛け合わせて作成します。

想定される計算

どのような値になりうるか想像してみましょう。
例えば

camRight = vec3(1.0, 0.0, 0.0)
camUp = vec3(0.0, 1.0, 0.0)
viewDir = vec3(0.0, 0.0, -1.0)
pixelPos = vec2(0.5, 0.5)

とすると、

pixelPos.x * camRight = 0.5 * vec3(1.0, 0.0, 0.0) = vec3(0.5, 0.0, 0.0)
pixelPos.y * camUp = 0.5 * vec3(0.0, 1.0, 0.0) = vec3(0.0, 0.5, 0.0)
CAM_FOV_FACTOR * viewDir = 4.0 * vec3(0.0, 0.0, -1.0) = vec3(0.0, 0.0, -4.0)

で、全て足し合わせて下記になります。

vec3(0.5, 0.0, 0.0) + vec3(0.0, 0.5, 0.0) + vec3(0.0, 0.0, -4.0) = vec3(0.5, 0.5, -4.0)

さらに正規化して下記になります

normalize(vec3(0.5, 0.5, -4.0)) = vec3(0.124, 0.124, -0.992)

render

vec3 color = render(camPos, rayDir)で、実際にレイマーチングを利用し、このピクセルに塗る色を確定しています。

vec3 render(in vec3 rayOrig, in vec3 rayDir) {
    vec3  lightDir = -rayDir; // miner's lamp
    vec3 resCol = vec3(0.0);
    float alpha = 1.0;
    for (float i = 0.0; i < MAX_RAY_BOUNCES; i++) {
        vec2 d = rayMarch(rayOrig, rayDir);
        float t = d.x;
        float mtlID = d.y;
        vec3 pos = rayOrig + t*rayDir;
        vec3 nrm = normal(pos);
        vec3 ref = reflect(rayDir, nrm);
        vec3 mtlDiffuse = getMaterialColor(mtlID);
        float diffuse = clamp(dot(nrm, lightDir), 0.0, 1.0);
        float specular = pow(clamp(dot(ref, lightDir), 0.0, 1.0), SPEC_POWER);
        diffuse *= shadow(pos, lightDir, DIST_EPSILON, MAX_SHADOW_DIST);
        vec3 col = mtlDiffuse*(AMBIENT_COLOR + LIGHT_COLOR*(diffuse + specular*SPEC_COLOR));
        col = applyFog(col, t);
        resCol += col*alpha; //  blend in (a possibly reflected) new color 
        if (mtlID <= MTL_BAUBLE || abs(dot(nrm, rayDir)) < 0.1) break;
        rayOrig = pos + ref*DIST_EPSILON;
        alpha *= BAUBLE_REFLECTIVITY;
        rayDir = ref;
    }
    return vec3(clamp(resCol, 0.0, 1.0));
}

この辺は特に言うことはないです

vec3  lightDir = -rayDir; // miner's lamp
vec3 resCol = vec3(0.0);
float alpha = 1.0;

ここが画面描画の主要部分になります。

for (float i = 0.0; i < MAX_RAY_BOUNCES; i++) {
    vec2 d = rayMarch(rayOrig, rayDir);
    float t = d.x;
    float mtlID = d.y;
    vec3 pos = rayOrig + t*rayDir;
    vec3 nrm = normal(pos);
    vec3 ref = reflect(rayDir, nrm);
    vec3 mtlDiffuse = getMaterialColor(mtlID);
    float diffuse = clamp(dot(nrm, lightDir), 0.0, 1.0);
    float specular = pow(clamp(dot(ref, lightDir), 0.0, 1.0), SPEC_POWER);
    diffuse *= shadow(pos, lightDir, DIST_EPSILON, MAX_SHADOW_DIST);
    vec3 col = mtlDiffuse*(AMBIENT_COLOR + LIGHT_COLOR*(diffuse + specular*SPEC_COLOR));
    col = applyFog(col, t);
    resCol += col*alpha; //  blend in (a possibly reflected) new color 
    if (mtlID <= MTL_BAUBLE || abs(dot(nrm, rayDir)) < 0.1) break;
    rayOrig = pos + ref*DIST_EPSILON;
    alpha *= BAUBLE_REFLECTIVITY;
    rayDir = ref;
}

MAX_RAY_BOUNCESはレイの最大反射回数で今回は3が入っているので、3回実行されます。
（3回まで光の反射を計算すると言う意味で、レイマーチングの光を進める処理とはまた違います。）

vec2 d = rayMarch(rayOrig, rayDir);

vec2 dはレイが進んだ距離（t）とマテリアルのID(mtlID)を格納する2次元ベクトルです。

vec3 posはレイの原点からレイの向きに距離tだけ進んだ結果です。原点を中心にしてどの方向にどれだけ移動した先に物体があるかを表す3次元ベクトルです。

vec3 nrmはposの法線ベクトルです。次の反射の計算に利用します。

vec3 refではglslのビルトイン関数であるreflectを利用しています。

引数に入力ベクトルとvec3 nrmで定義した法線ベクトルを渡すと反射面における反射ベクトルを返してくれます。

vec3 mtlDiffuseはマテリアルのカラーをマテリアルのIDから取得しています。
（なんでmtlDiffuseなのかはわからないです...実装的にはmtlColで良い気が）

float diffuseは光の拡散の計算を行っています。

float diffuse = clamp(dot(nrm, lightDir), 0.0, 1.0);
diffuse *= shadow(pos, lightDir, DIST_EPSILON, MAX_SHADOW_DIST);

diffuseの説明は下記です。

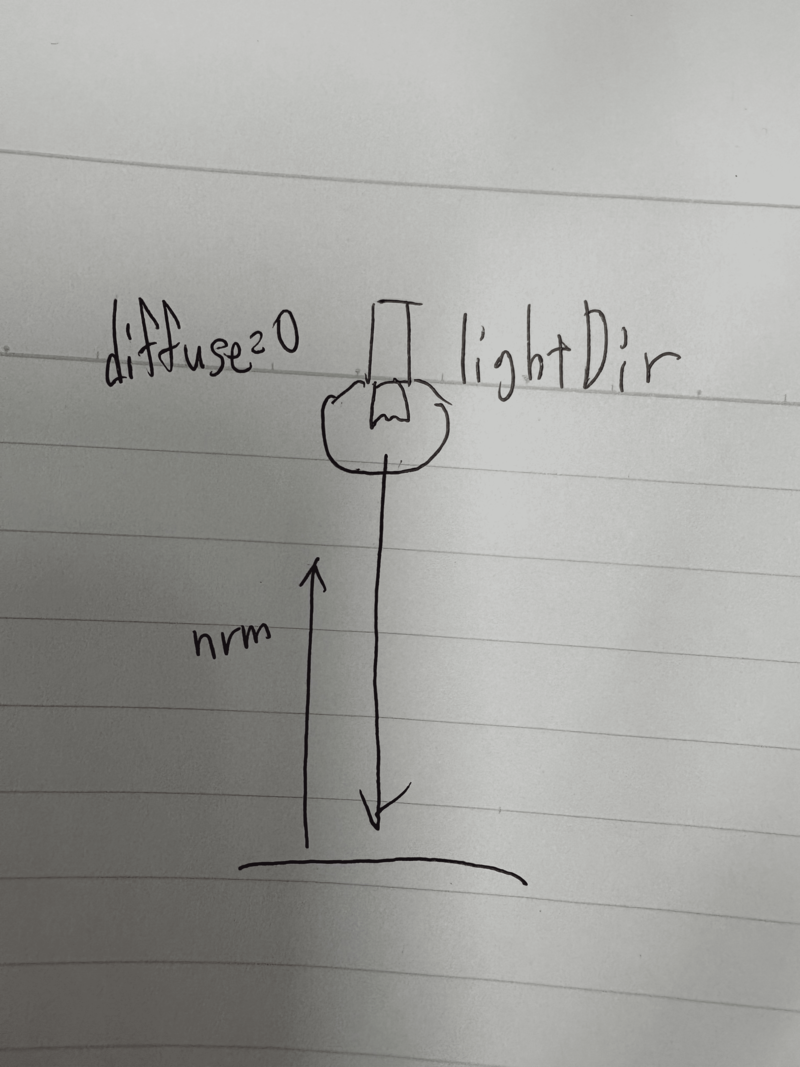
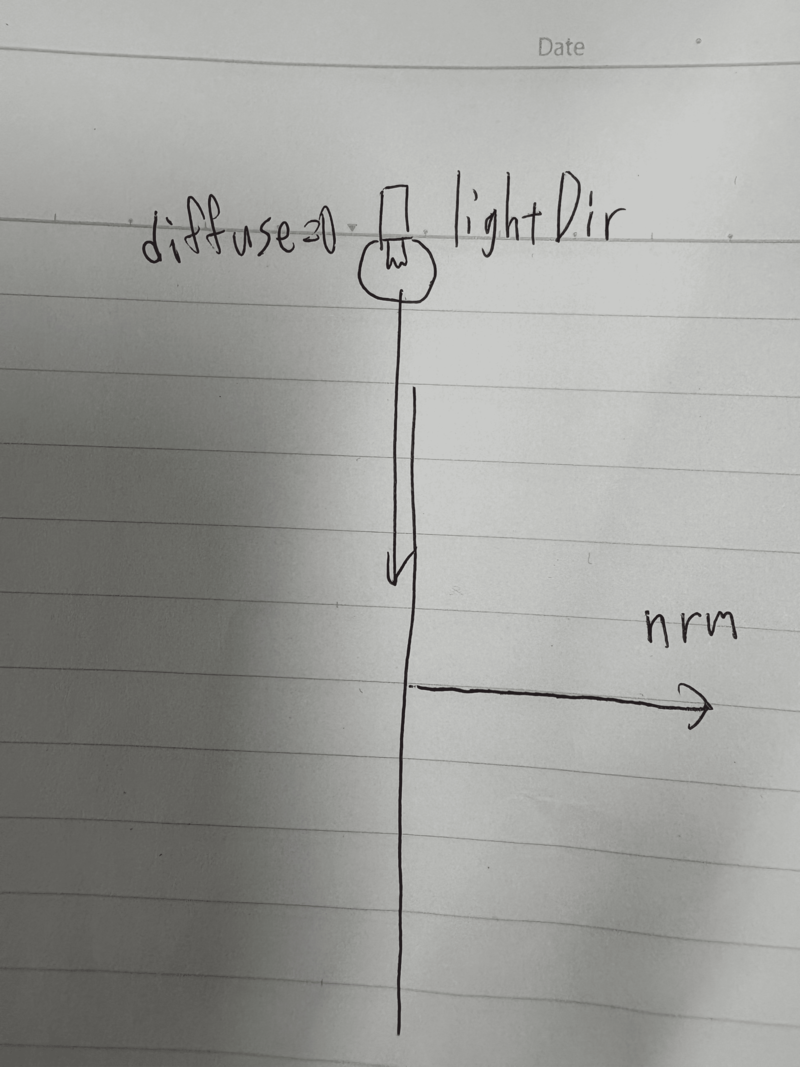
法線ベクトルと光の向きの内積を0~1の範囲に制限しています。
なぜ法線ベクトルと光の向きの内積で光の拡散が求められるのかの説明は下記を見ればわかるかと思います。

自分でメモった説明用の画像がこちらです。
拡散が発生しない角度 or 光が当たらない場合はdiffuseが0。そうでない場合はdiffuseが正になります。

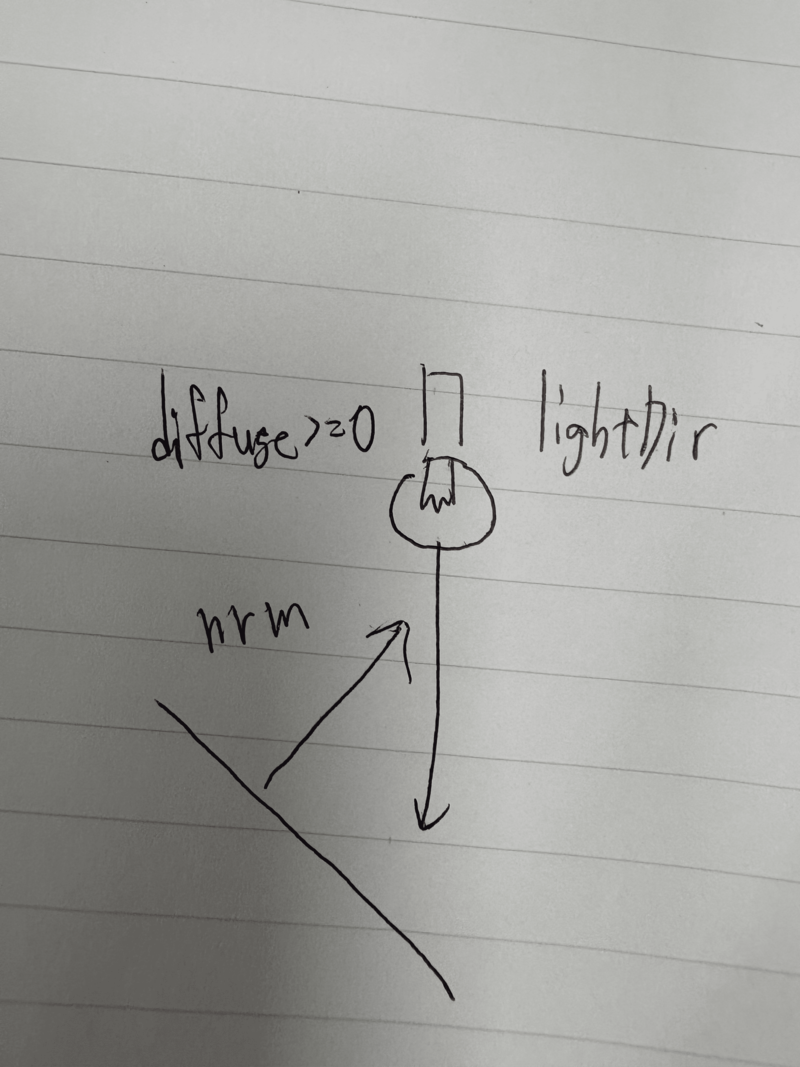
上記の処理を行った上で、光によって生まれる影の計算も掛け合わせています。

こちらはスペキュラと呼ばれるマテリアルに当たった光のうち、反対方向に反射する光を定義する処理です。

float specular = pow(clamp(dot(ref, lightDir), 0.0, 1.0), SPEC_POWER);

概要に関しては下記を参考にしてください。

やってることは先ほどのdiffuseに近いです。法線ベクトル（≒物体の向き）との内積ではなく、反射との内積を求めているのが違う部分です。
後、光の強さを調整するために求めた値をSPEC_POWER乗しています。

ここは色の決定を行う部分です。

vec3 col = mtlDiffuse*(AMBIENT_COLOR + LIGHT_COLOR*(diffuse + specular*SPEC_COLOR));
col = applyFog(col, t);

マテリアルの色、光の色、diffuse、specularをそれぞれ計算してピクセルに塗るべき色を作ります。
色とレイが進んだ距離から霧の量を決定して描画しています。

こちらはボブルのための分岐処理です。
ボブルの反射が強すぎると綺麗な見た目にならないので反射を弱めています。

if (mtlID <= MTL_BAUBLE || abs(dot(nrm, rayDir)) < 0.1) break;
rayOrig = pos + ref*DIST_EPSILON;
alpha *= BAUBLE_REFLECTIVITY;
rayDir = ref;

この処理を消すとこうなる

戻すとこう

rayMarch

次はレイマーチングで3d空間を擬似的に作っている部分のロジックを見ていきましょう。

vec2 rayMarch(in vec3 rayOrig, in vec3 rayDir) {
    float t = NEAR_CLIP_PLANE;
    float mtlID = MTL_BACKGROUND;
    for (int i = 0; i < MAX_RAYCAST_STEPS; i++) {
        vec2 d = distf(rayOrig + rayDir*t);
        if (d.x < DIST_EPSILON || t > FAR_CLIP_PLANE) break;
        t += d.x*STEP_DAMPING;
        mtlID = d.y;
    }

    if (t > FAR_CLIP_PLANE) mtlID = MTL_BACKGROUND;
    return vec2(t, mtlID);
}

float tはレイの始点からの距離を表します。今回は初期値1からスタートします。
float mtlIDは何にも衝突しなければ背景ということで初期値はMTL_BACKGROUNDになっています。

その後、MAX_RAYCAST_STEPSの回数分までレイを進行させながらマテリアルと交差するかどうかを確認していきます。

distfについては後ほど説明しますが、ここで物体とレイとの距離を出しています。
vec2 d = vec2(距離, mtlID)なので、距離を利用したい場合はd.xを呼び出し、マテリアルのIDが欲しい場合はd.yを呼び出します。

vec2 d = distf(rayOrig + rayDir*t);

ここはマテリアルとレイとの距離がすでに必要なだけ近い場合か遠すぎる場合に処理を終了するための分岐です。

if (d.x < DIST_EPSILON || t > FAR_CLIP_PLANE) break;

for文内の終わりの方でレイを前に進めて、交差しているmtlIDを設定しています。

t += d.x*STEP_DAMPING;
mtlID = d.y;

normal

名前の通り法線ベクトルを求めるための関数です。
ただ、処理が結構わかりづらいので、下記のサイトで法線ベクトルの公式の導出について学ぶと似たようなことをやっているとわかるかと思います。

vec3 normal(in vec3 p)
{
    # NORMAL_EPSは0.001
    vec2 d = vec2(NORMAL_EPS, 0.0);
    return normalize(vec3(
        distf(p + d.xyy).x - distf(p - d.xyy).x,
        distf(p + d.yxy).x - distf(p - d.yxy).x,
        distf(p + d.yyx).x - distf(p - d.yyx).x));
}

微小な変位を表すvec2 dを利用し、
x,y,z方向の微分をそれぞれ近似して正規化して法線ベクトルを求めています。

getMaterialColor

先ほどとは打ってかわってシンプルな関数です。

vec3 getMaterialColor(float matID) {
    vec3 col = CLR_BACKGROUND;
         if (matID <= MTL_GROUND) col = vec3(3.3, 3.3, 4.5);
    else if (matID <= MTL_NEEDLE) col = vec3(0.152,0.36,0.18);
    else if (matID <= MTL_STEM)   col = vec3(0.79,0.51,0.066);
    else if (matID <= MTL_TOPPER) col = vec3(1.6,1.0,0.6);
    else if (matID <= MTL_CAP)    col = vec3(1.2,1.0,0.8);
    else                          col = jollyColor(matID);
    return col;
}

マテリアルIDごとに色を決定しています。
BAUBLEに関しては色をそれぞれランダムに変更するためjollyColorにさらに渡して処理しています。

shadow

rayMarchと似た処理でマテリアルの影を計算します。
今まで説明してきた技術の組み合わせなので特に言うことはないです。

float shadow(in vec3 rayOrig, in vec3 rayDir, in float tmin, in float tmax) {
    float shadowAmt = 1.0;
    float t = tmin;
    for (int i = 0; i < MAX_RAYCAST_STEPS; i++) {
        float d = distf(rayOrig + rayDir*t).x*STEP_DAMPING;
        shadowAmt = min(shadowAmt, 16.0*d/t);
        t += clamp(d, 0.01, 0.25);
        if (d < DIST_EPSILON || t > tmax) break;
    }

    return clamp(shadowAmt, 0.0, 1.0);
}

applyFog

今塗ろうとしているピクセルの元々の色とカメラからの距離を計算して霧のような効果を演出する関数です。

vec3 applyFog(vec3 col, float dist) {
    return mix(col, CLR_BACKGROUND, 1.0 - exp(-FOG_DENSITY*dist*dist));
}

mix関数でcolと背景色を補間しています。
補間の条件(1.0 - exp(-FOG_DENSITY*dist*dist))は説明が難しいので省略しますが距離が離れるほど値が大きくなる（霧が濃くなる）と考えてもらえればと思います。

distf

前に表示されているものが画面に描画されるように、マテリアルとカメラとの距離を測って一番前にあるものを描画するための関数です。

vec2 distf(in vec3 pos) {
    vec2 res = ground(pos);
    
    vec2 tr = tree(pos);
    add(res, tr);
    
    vec2 top = topper(pos);
    add(res, top);
    
    vec2 b = baubles(pos);
    add(res, b);
    return res;
}

add(res, tr)などでresを上書きしています。

jollyColor

Baubleの色を決定するためにmatIDをもとにYIQの色空間で色を作成します。

vec3 jollyColor(float matID) {
    vec3 clr = cos(matID*BAUBLE_YIQ_MUL);
    clr= clr*vec3(0.1, BAUBLE_CLR_I, BAUBLE_CLR_Q) + vec3(BAUBLE_CLR_Y, 0.0, 0.0);
    return clamp(clr*YIQ_TO_RGB, 0.0, 1.0);
}

詳しい理由は作者本人でないとわかりませんが、YIQ色空間は元々テレビ放送で利用されており、視覚的に自然な色が利用されているのでオーナメントの色をランダムかつ違和感のないものにするためにちょうど良かったのではと考えています。

SDFのコードを理解する

ここからは各マテリアル（地面、ツリー、星、オーナメント）を作っていきます。
プリミティブな距離関数に関しては説明しませんが、下記を見ていただければと思います。

ground

地面の距離関数です。
複雑な凹凸を作るためにsin,cosを組み合わせています。

vec2 ground(in vec3 p) {
    p.y += (sin(sin(p.z*0.1253) - p.x*0.371)*0.31 + cos(p.z*0.553 + sin(p.x*0.127))*0.12)*1.7 + 0.2;
    return vec2(p.y, MTL_GROUND);
}

star

星の距離関数です。
平面のSDFを折りたたんで星を作っています。

float star(vec3 p) {
    p.xy = repeatAng(p.xy, 5.0);
    p.xz = abs(p.xz);
    return plane(p, vec3(0.5, 0.25, 0.8), -0.09);
}

p.xz = abs(p.xz);で負の値をなくして一定のタイミングで折りたたみ、
p.xy = repeatAng(p.xy, 5.0);で5回回転させながら繰り返しています。

tree

cone（円錐）を真ん中に配置し、周りに枝を配置してツリーを作成しています。

vec2 tree(vec3 p) {
    //  the first bunch of branches
    vec2 res = halfTree(p); 
    
    // the second bunch of branches (to hide the regularity)
    p.xz = rotate(p.xz, TREE2_ANGLE);
    p.y -= BRANCH_SPACING*TREE2_OFFSET;
    p /= TREE2_SCALE;
    vec2 t2 = halfTree(p);
    t2.x *= TREE2_SCALE;
    add(res, t2);

    // trunk    
    vec2 tr = vec2(cone(p.xyz, TRUNK_WIDTH, TREE_H*2.0), MTL_STEM);
    add(res, tr);

    res.x = intersect(res.x, sphere(p - vec3(0.0, TREE_H*0.5 + 1.0, 0.0), TREE_H + 1.0));    
    return res;
}

cone

halftree（一つ目）

halftree一つだと規則性が見えてしまうので、位置や大きさを調整してもう一つ追加しています。

こちらはツリーの形状を整えるために球体を作って枝が生える範囲を制限しています。

res.x = intersect(res.x, sphere(p - vec3(0.0, TREE_H*0.5 + 1.0, 0.0), TREE_H + 1.0)); 

ツリーの完成系

halftree(branch, needle)

針葉樹っぽい感じなので葉っぱ（針）と枝を作成しています。
回転させながら大量に配置してhalftreeを作っています。

float needles(in vec3 p) {
    p.xy = rotate(p.xy, -length(p.xz)*NEEDLE_TWIST);
    p.xy = repeatAng(p.xy, NEEDLES_RADIAL_NUM);
    p.yz = rotate(p.yz, -NEEDLE_BEND);
    p.y -= p.z*NEEDLE_GAIN;
    p.z = min(p.z, 0.0);
    p.z = repeat(p.z, NEEDLE_SPACING);
    return cone(p, NEEDLE_THICKNESS, NEEDLE_LENGTH);
}

vec2 branch(in vec3 p) {
    vec2 res = vec2(needles(p), MTL_NEEDLE);
    float s = cylinder(p.xzy + vec3(0.0, 100.0, 0.0), vec2(STEM_THICKNESS, 100.0));
    vec2 stem = vec2(s, MTL_STEM);
    add(res, stem);
    return res;
}

vec2 halfTree(vec3 p) {
    float section = floor(p.y/BRANCH_SPACING);
    float numBranches =  max(2.0, BRANCH_NUM_MAX - section*BRANCH_NUM_FADE);
    p.xz = repeatAng(p.xz, numBranches);
    p.z -= TREE_R*TREE_CURVATURE;
    p.yz = rotate(p.yz, BRANCH_ANGLE);
    p.y = repeat(p.y, BRANCH_SPACING);
    return branch(p);
}

needlesは円錐を回転させて曲げて繰り返して作成しています。
branchはcylinder（円柱）にneedlesを周辺に配置して作成しています。
その上でhalftreeはbranchを回転させながら位置を調整して配置する最終的な処理をしています。

bauble

オーナメントの距離関数です。

vec2 bauble(in vec3 pos, float matID) {
    float type = mod(matID, 5.0);
    float d = sphere(pos, BAUBLE_SIZE);
    if (type <= 1.0) {
        // bumped sphere
        d += cos(atan(pos.x, pos.z)*30.0)*0.01*(0.5 - pos.y) + sin(pos.y*60.0)*0.01;
    } else if (type <= 2.0) {
        // dented sphere
        d = diff(d, sphere(pos + vec3(0.0, 0.0, -0.9), 0.7));
    } else if (type <= 3.0) {
        // horisontally distorted sphere
        d  += cos(pos.y*28.0)*0.01;
    } else if (type <= 4.0) {
        // vertically distorted sphere
        d += cos(atan(pos.x, pos.z)*20.0)*0.01*(0.5 - pos.y);
    }

    vec2 res = vec2(d, matID);
    //  the cap 
    pos = translate(pos, vec3(0.0, BAUBLE_SIZE, 0.0));
    float cap = cylinder(pos, vec2(BAUBLE_SIZE*0.2, 0.1));
    //  the hook
    cap = add(cap, torus(pos.xzy - vec3(0.0, 0.0, 0.12), BAUBLE_SIZE*0.1, 0.015));
    vec2 b = vec2(cap, MTL_CAP);
    add(res, b);
    return res;
}

float type = mod(matID, 5.0);
float d = sphere(pos, BAUBLE_SIZE);
if (type <= 1.0) {
    // bumped sphere
    d += cos(atan(pos.x, pos.z)*30.0)*0.01*(0.5 - pos.y) + sin(pos.y*60.0)*0.01;
} else if (type <= 2.0) {
    // dented sphere
    d = diff(d, sphere(pos + vec3(0.0, 0.0, -0.9), 0.7));
} else if (type <= 3.0) {
    // horisontally distorted sphere
    d  += cos(pos.y*28.0)*0.01;
} else if (type <= 4.0) {
    // vertically distorted sphere
    d += cos(atan(pos.x, pos.z)*20.0)*0.01*(0.5 - pos.y);
}

タイプは5パターン用意して、通常の球と見た目の違うものが4パターンという形で作成しています。

vec2 res = vec2(d, matID);
//  the cap 
pos = translate(pos, vec3(0.0, BAUBLE_SIZE, 0.0));
float cap = cylinder(pos, vec2(BAUBLE_SIZE*0.2, 0.1));
//  the hook
cap = add(cap, torus(pos.xzy - vec3(0.0, 0.0, 0.12), BAUBLE_SIZE*0.1, 0.015));
vec2 b = vec2(cap, MTL_CAP);
add(res, b);

上についているキャップとフックをcylinder（円柱）とtorus（ドーナツ型）の距離関数で作成しています。

baubles

baubleを回転させながらツリーの形に合わせて配置する関数です。
halftree`と似た処理になっています。

vec2 baubles(in vec3 p) {
    vec3 pos = p;
    float h = abs(-floor(pos.y/BAUBLE_SPACING)/TREE_H + 1.0)*TREE_R;
    float nb = max(1.0, floor(BAUBLE_COUNT_FADE1*(h + BAUBLE_COUNT_FADE2)*h));
    vec3 rp = repeatAngS(pos.xz, nb);
    float matID = (h + rp.z + BAUBLE_MTL_SEED)*117.0;
    pos.xz = rp.xy;
    pos.y = repeat(pos.y, BAUBLE_SPACING);
    pos.y += mod(matID, 11.0)*BAUBLE_JITTER;
    pos.z += -h + BAUBLE_SPREAD;
    vec2 res = bauble(pos, matID);
    res.x = intersect(res.x, sphere(p - vec3(0.0, TREE_H*0.5 + 0.5, 0.0), TREE_H + 0.5));
    return res;
}

最後に

クリスマスツリーをレイマーチングで作成するコードの解説はこれで終わりです。
実装を全て説明するのは大変でしたが自分の理解度も深まって良かったです。

今回add, intersect, diffやアフィン変換（rotateなど）のロジックは説明しませんでしたが、これらはシェーダでレイマーチングをやる上での土台の部分なので自分と同じシェーダ初心者は頑張って覚えてみてください。

参考資料

今回記事内で紹介した資料