「機械学習の数理 Advent Calendar 2018」の六日目の記事です。またこれは機械学習工学 / MLSE Advent Calendar 2018に書いた「テンソル分解を用いた教師無し学習による変数選択」の続編でもあります。なので「はじめに」と「テンソル」のところはそっちで読んでから「問題設定」を読んでください。すみません。
[Springerから本をだしました!]
(https://www.springer.com/jp/book/9783030224554)読んでもらえると嬉しいです!
はじめに
テンソル
問題設定
ここでは$K$個の共通サンプルがあり、それに対して独立な$N,M$種類の測定が得られたとします。わかりやすい例としてはサンプルが時刻で、各時刻に2種類の静止画が紐づけられている場合などがあるでしょう。これらはそれぞれ$x_{ik} \in \mathbb{R}^{N \times K}$及び$x_{jk} \in \mathbb{R}^{M \times K}$の行列の形であるとしましょう。画像の例で言えば時刻$k$での$i$番目、または、$j$番目のピクセルの値、ということになると思います。さて、ここで次の様な問題を考えます。「実は$N$個と$M$個の変数には意味がある変数と意味がない変数が混じっている。意味がある変数のペアの場合、$x_{ik}$と$x_{jk}$には有意の相関があるがそうでない場合は相関していない。どの$i$と$j$が相関しているか(意味がある変数か)?」
では具体的に模擬データを使ってやってみましょう。
$$
x_{ik}\sim k+\mathcal{N}(\mu,\sigma), i \leq N_1 ;
$$
$$
x_{jk}\sim k+\mathcal{N}(\mu,\sigma), j \leq M_1 ;
$$
$$
x_{ik},x_{jk} \sim \mathcal{N}(\mu,\sigma), \mbox{otherwise}
$$
つまり、$i<N_1,j<M_1$の変数だけが$k$に対する単調性を共有することを介して相関していて($N_1 \times M_1$ペア)、あとは相関していない、という状況を考えるわけです。普通に考えたらここはペアワイズで相関係数を計算し、有意に相関しているペアを選ぶ、と考えるでしょう。では実際に、やってみます。$N=M=100,K=6,N_1=M_1=10,\mu=\sigma=1$とします。この設定だと全ペアは10000個あり、そのうち100ペアだけが相関しているという設定になります。
相関係数が有意にノンゼロであるかどうかは相関係数を$r$としたとき、$t=\frac{r(K-2)}{\sqrt{1-r^2}}$が自由度$K-2$のt分布に従うという性質をつかって$P$値を計算し、Benjamini-Hochberg法で多重比較補正してから補正$P$値が0.05以下の相関係数をもつペアを探すという方法をとります。
set.seed(0)
N<-100
N1<-10
M<-100
M1<-10
K<-6
x <- matrix(rnorm(K*N), K,N)
y <- matrix(rnorm(K*M), K,M)
x[,1:N1] <-x[,1:N1]+1:K
y[,1:M1] <-y[,1:M1]+1:K
COR <- cor(x,y)
tt <-COR*(K-2)/sqrt(1-COR^2)
P <-pt(tt,df=K-2,lower.tail=F)
label <- matrix(F,N,M)
label[1:10,1:10]<-T
table(label,p.adjust(P,"BH")<0.05)
label FALSE TRUE
FALSE 9860 40
TRUE 84 16
結果は
| 相関 | 無相関 | |
|---|---|---|
| $i \leq N_1$かつ$j \leq M_1$ | 16 | 84 |
| それ以外 | 40 | 9860 |
という感じです(行が正解、列が予測の混同行列)。勿論、統計的には十分有意な結果は出せています。ですが、決して、すごくいいかというと問題です(16というのが予測と正解が一致した数です)。なにより、40ペアも擬陽性が入ってしまっています(真陽性より多い!)。
テンソル分解を用いた教師無し学習による変数選択
じゃあ、これをテンソル分解でやってみましょう。このままだと行列なので強引にテンソルの格好に変更します。
$$
x_{ijk} = x_{ik}x_{jk}
$$
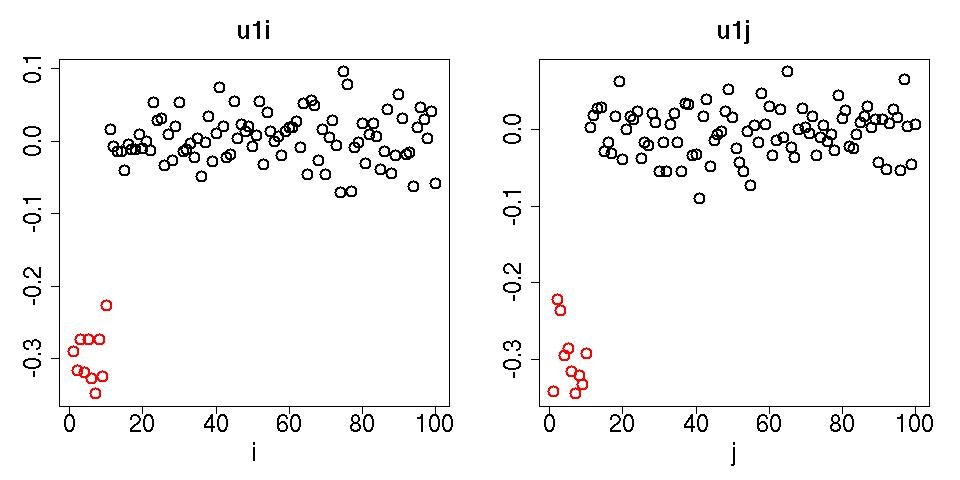
これにテンソル分解を適用し$u_{1i},u_{1j}$を見てみましょう。
Z <- array(NA,c(100,100,6))
for (i in c(1:6))
{
Z[,,i] <- data.matrix(outer(x[i,],y[i,],"*"))
}
require(rTensor)
HOSVD <- hosvd(as.tensor(Z))
jpeg(file="fig2.jpg",width=960,height=480)
par(mfrow=c(1,2))
plot(HOSVD$U[[1]][,1],col=c(rep(2,10),rep(1,90)),cex=2,lwd=2,xlab="i",cex.axis=2,ylab="",main="u1i",cex.main=2,cex.lab=2)
plot(HOSVD$U[[2]][,1],col=c(rep(2,10),rep(1,90)),cex=2,lwd=2,xlab="j",cex.axis=2,ylab="",main="u1j",cex.main=2,cex.lab=2)
par(mfrow=c(1,1))
dev.off()
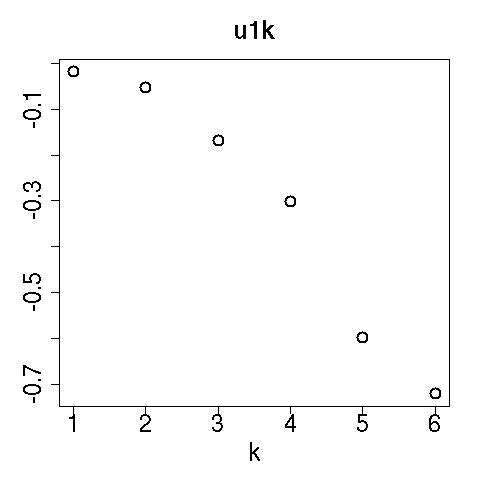
赤く描かれた$i\leq N_1,j\leq<M_1$の変数がきちっと区別されて大きな絶対値をとっていることがわかります。つまり、入れ込んだ相関がちゃんと検出されている。ペアワイズの相関係数による検出の時とは大違いです。なんでこんな都合よくいったかというとそれは$u_{1k}$を見るとわかります。
jpeg(file="fig3.jpg")
plot(HOSVD$U[[3]][,1],cex=2,lwd=2,xlab="k",cex.axis=2,ylab="",main="u1k",cex.main=2,cex.lab=2)
dev.off()
見ての通り$u_{1k}$はデータを作るときに入れ込んだ$k$依存性をちゃんと拾っています。そして$G(1,1,1)$は$G(1,\ell_2,\ell_3)$の中でもっとも絶対値が大きいのです。テンソル分解の式の右辺を見ると$G$は重みの役目をしています。$G(1,1,1)$の値が最大、ということは$\ell_1=\ell_2=\ell_3=1$を掛けた項がもっとも寄与が大きいということです。なので$k$依存性を表現している$u_{1k}$とペアになっている$u_{1i}$や$u_{1j}$を見ることで$k$依存性を共有している=相関しているペアが検出できる、というわけです。
いかがでしょうか?実に簡単でしょう?ペアワイズな比較を行うと、数が増えてしまい、多重比較補正を考えるとなかなか厳しいことになります。今回のパラメーター設定ではそういうことは起きなかったのですが、代わりに擬陽性がとても増えてしまいました。もともと、ペアの数は100×100=10000個もありますから、補正された$P$値を0.01に抑えても10000個の1%の100個程度の間違いは避けられません。実際、表にはそれくらいの数の擬陽性が出てしまっていますが、これは妥当な結果なのです。ペアワイズな検定はどうしても正例の数が負例の数に比べて少なくなりがちで、その結果擬陽性をさけるのが難しいです。ですが、テンソル分解を使うとペアワイズな比較をせずにペアを見つけることが可能な場合があるので、ぜひ、使ってみてほしいです。
以下の「参考文献」と記されたリンク先はこんな「テンソル分解を用いた教師無し学習による変数選択」を使って僕がバイオインフォの研究をした論文たちです。読んでもらえるとうれしいです。
参考文献
おまけ
別に論文じゃないのでここまでやらなくてもいいのですが、一応、100回繰り返して平均した場合の混同行列。
※ペアワイズな相関関数
| 相関 | 無相関 | |
|---|---|---|
| $i \leq N_1$かつ$j \leq M_1$ | 17.06 | 82.94 |
| それ以外 | 41.25 | 9858.75 |
というわけで一回やった時とあんまり変わりませんでした。擬陽性(41.257個)が真陽性(17.063個)よりずっと多いです。
※テンソル分解を用いた教師無し学習による変数選択
| 補正$P$値 | $P<0.1$ | $P \geq 0.1$ | 補正$P$値 | $P<0.1$ | $P \geq 0.1$ |
|---|---|---|---|---|---|
| $i \leq N_1$ | 5.98 | 4.02 | $j \leq M_1$ | 6.47 | 3.53 |
| それ以外 | 0.00 | 90.0 | それ以外 | 0.00 | 90.0 |
「テンソル分解を用いた教師無し学習による変数選択」の$P$値は$u_{1i},u_{1j}$が正規分布しているという帰無仮説の元にχ二乗分布を用いて
$$
P_i = P_{\chi^2} \left [ > \left( \frac{u_{1i}}{\sigma_{1i}}\right)^2\right]
$$
及び
$$
P_j = P_{\chi^2} \left [ > \left( \frac{u_{1j}}{\sigma_{1j}}\right)^2\right]
$$
で計算しました。ここで$\sigma_{1i},\sigma_{1j}$は$u_{1i},u_{1j}$の標準偏差、であり$u_{1i},u_{1j}$は平均がゼロになるように変換してから標準偏差を計算して上記の式に代入するものとしました。$P_{\chi^2}[>x]$は引数が$x$より大きい場合のχ二乗分布の累積確率です。
相関係数に比べてかなり良いように見えます。何より擬陽性が全くありません。これは上図に見るように、$i \leq N_1$と$j \leq M_1$の$P$値が、$i > N_1$と$j > M_1$の$P$値より必ず小さいからです。ただ、これは補正$P$値が0.1以下という基準で切っているのであれです。もっとも、ペアワイズな相関関数の時の様に$i \leq N_1, j \leq M_1$とそれ以外で$P$値が逆転しているわけじゃないので閾値の$P$値を大きくしていっても擬陽性は現れず、ある値で100%相関のある変数と無い変数を判別することができることは注意すべきでしょう。
N<-100
N1<-10
M<-100
M1<-10
K<-6
p1 <- NULL
p2 <- NULL
p3<- NULL
for (i in c(1:100))
{
cat(i, "\n")
x <- matrix(rnorm(K*N), K,N)
y <- matrix(rnorm(K*M), K,M)
x[,1:N1] <-x[,1:N1]+1:K
y[,1:M1] <-y[,1:M1]+1:K
COR <- cor(x,y)
tt <-COR*(K-2)/sqrt(1-COR^2)
P <-pt(tt,df=K-2,lower.tail=F)
p1 <- cbind(p1,p.adjust(P,"BH"))
Z <- array(NA,c(100,100,6))
for (i in c(1:6))
{
Z[,,i] <- data.matrix(outer(x[i,],y[i,],"*"))
}
HOSVD <- hosvd(as.tensor(Z))
P <- pchisq(scale(HOSVD$U[[1]][,1])^2,1,lower.tail=F)
p2 <- cbind(p2,p.adjust(P,"BH"))
P <- pchisq(scale(HOSVD$U[[2]][,1])^2,1,lower.tail=F)
p3<- cbind(p3,p.adjust(P,"BH"))
}
pic <- matrix(F,100,100)
pic[1:10,1:10] <- T
pic <- as.vector(pic)
t1 <- p1<0.05
TP <- sum(t1[pic])/100
FN <- 100-TP
FP <- sum(t1[!pic])/100
TN <- 9900-FP
matrix(c(TP,FP,FN,TN),2)
[,1] [,2]
[1,] 17.06 82.94
[2,] 41.25 9858.75
t2 <- p2<0.1
TP <- sum(rowSums(t2)[1:10])/100
FN <- 10-TP
FP <- sum(rowSums(t2)[11:90])/100
TN <- 90-FP
matrix(c(TP,FP,FN,TN),2)
[,1] [,2]
[1,] 5.98 4.02
[2,] 0.00 90.00
t3 <- p3<0.1
TP <- sum(rowSums(t3)[1:10])/100
FN <- 10-TP
FP <- sum(rowSums(t3)[11:90])/100
TN <- 90-FP
matrix(c(TP,FP,FN,TN),2)
[,1] [,2]
[1,] 6.47 3.53
[2,] 0.00 90.00