概要
以前、GoogleAppsScriptで緯度経度から距離計算するコードを書いた。
GoogleMapの距離測定と同じ結果が欲しかったので、何かの記事で見た「GoogleMapは地球を半径6378137mの球体として距離計算している」と言うのを参考にして定数を設定。
それらしい計算結果にはなるんだけど、GoogleMapの距離測定と比べて常に0.11%の誤差が出てしまう・・・もしかして地球の大きさが違う?
と言うわけで、GoogleMapの距離測定から地球の大きさを逆算してみた。
距離計算についてはコチラで解説。
Qiita記事:緯度経度からの距離計算 ヒュベニより航海算法の方が高精度説
判定方法
GoogleMapで距離測定して、同じ位置で距離を計算した時の誤差を評価する。
参考位置とGoogleMapでの距離測定。

計算に使う定数(地球の半径)を変えながら4つの距離を計算し、合算の13859.08kmに近いほどGoogleMapの地球の大きさに近づいていると考える。
1km刻み
地球の半径を1kmずつ変えながら計算。
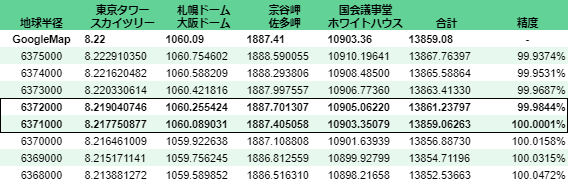
6371000m~6372000mの間に正解がありそう。「地球の半径」でググると6371kmと出るので良い感じかも^^
100m刻み
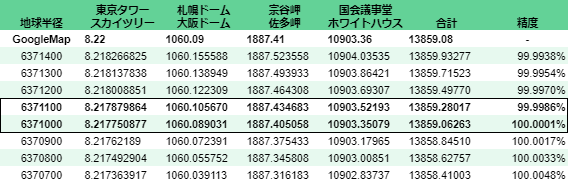
6371000mが強い!誤差の合算は約20m(0.0001%)。
もっと刻む。
10m刻み
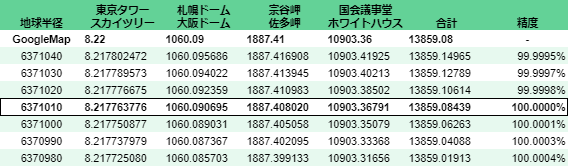
6371010mでほぼ誤差なし!でも、国会議事堂~ホワイトハウス間をGoogleMapの桁に揃えると、まだ10mの誤差がある。
更に刻もう。
1m刻み
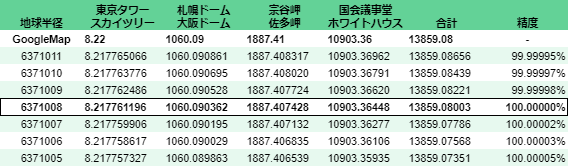
精度が100.0000%だらけになったので1桁増やしてみた。6371008mが一番近い。GoogleMapと桁を揃えた時の誤差もゼロ。
せっかくなので、もうちょっと刻んでみる。
10cm刻み
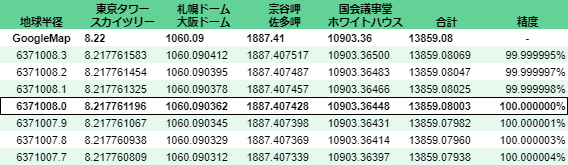
更に精度を1桁アップ。結果は変わらず、これはもう6371008mで良いんじゃないかな。
結論
GoogleMapは(たぶん)地球を半径6371008mの球体として距離計算している!
なのでGooglemapの距離測定と同じ結果を得るためのコードはこんな感じ。
function googleGeosail(LatA,LngA,LatB,LngB){
with(Math){
var i = PI/180;
var r = 6371.008;
var X = acos(sin(latA*i)*sin(latB*i)+cos(latA*i)*cos(latB*i)*cos(lngA*i-lngB*i))*r;
}
return X;
}
A地点の緯度,経度とB地点の緯度,経度を引数に、2点間の距離 X(km)を返す。
測地線航海算法の変形なんだけど、なぜこうなるかは下記の記事で解説。
Qiita記事:【ワンライナー】緯度経度から1行で距離計算
おまけ
「6371008m」の根拠を考察。
楕円体には平均半径と言う考え方があるらしく、たぶんそれだろうと当たりをつけてみた。
長半径(赤道半径)a と短半径(極半径)b から回転楕円体(地球)の体積を計算し、体積が同じ球体の半径が平均半径となるので、次の式から求められる。
\begin{eqnarray}
回転楕円体の体積&:& V = \frac{4}{3}\pi a^2b\\
体積Vの球体の半径&:& r(V) = \sqrt[3]{3V/4\pi}\\
回転楕円体の平均半径&:& r = \sqrt[3]{a^2b}\\
\end{eqnarray}
地球の最良推定値(国際天文学連合が採用する実測値)で計算すると約6371000.4m、GRS80楕円体(GPSや地図作成などに用いられる測地系)で計算してみても約6371000.8mと微妙に合わない。(参考:地球の大きさ@wikipedia)
6371008はどこから来たんだろう?と思って調べていたら、
回転楕円体の平均半径:r = (2a+b)/3
として近似値を求める式があるみたい。
こっちの式で最良推定値から計算すると約6371008.4m! GRS80では約6371008.7となった。どうやらGoogleMapの地球は実測値を元に、近似式で求めた平均半径を半径とする球体っぽいε=( ̄。 ̄;A フゥ
余談だけど、気象庁が採用している地球半径は6371009mなので、GRS80の近似平均半径なのかも。
当初参考にした「GoogleMapは地球を半径6378137mの球体として距離計算している」と言う記事も、「GoogleMapは赤道半径6378137mの楕円体から平均半径を求めた球体として距離計算している」だったのかもしれない。
※10cm刻みで検証した時に半径6371008.1mの方が誤差が大きかったので、楕円体から平均半径を求めて距離計算しているのではなく、最初から平均半径を定数として球体の距離計算をしているものと思われる。