概要
緯度経度から2点間の距離を求めるとき、地球は楕円体なので球体の扁平率(球と比べてどれくらい潰れているか)を計算する必要がある。
ただGoogleMapでは、地球を半径6371008(m)の真球としているため、扁平率はゼロ( ゚д゚)!
Qiita記事:
【GoogleMap】地球を半径6371008mの球体として距離計算していた
緯度経度からの距離計算 ヒュベニより航海算法の方が高精度説
上記の記事で「測地線航海算法」を使って緯度経度から2点間の距離を求めるコードを紹介したけど、扁平率を考慮しなくて良いならかなり計算を省略できるなぁと思い立ったのがこの記事。
「地図上の2点間の距離計算ワンライナー」スタート!
基本形
まずは楕円体で計算するコードから。
function geosailing(lA,LA,lB,LB) {
//緯度経度をラジアンに変換
var latA = lA * (Math.PI/180);
var lngA = LA * (Math.PI/180);
var latB = lB * (Math.PI/180);
var lngB = LB * (Math.PI/180);
//定数
var A = 6371008; //長半径
var B = 6371008; //短半径
//扁平率(F)
var F = (A-B)/A;
//化成緯度(Φ)
var phiA = Math.atan(B/A * Math.tan(latA));
var phiB = Math.atan(B/A * Math.tan(latB));
//球面上の距離(X)
var X = Math.acos(Math.sin(phiA) * Math.sin(phiB) + Math.cos(phiA) * Math.cos(phiB) * Math.cos(lngA-lngB));
//距離補正量(Δρ)
var f1 = (Math.sin(X)-X) * Math.pow(Math.sin(phiA)+Math.sin(phiB),2) / Math.pow(Math.cos(X/2),2);
var f2 = (Math.sin(X)+X) * Math.pow(Math.sin(phiA)-Math.sin(phiB),2) / Math.pow(Math.sin(X/2),2);
var drho = F/8 * (f1-f2);
//測地線長(ρ)
var rho = A*(X+drho); //距離(m)
var rhokm = rho/1000; //距離(km)
return rhokm;
}
測地線航海算法の公式通り。
コメントアウトと改行を除くと、16行647文字。
扁平率ゼロ
GoogleMapで採用されている定数を定義しているので、長半径と短半径が等しく扁平率Fはゼロ。そのため化成緯度ΦのB/Aが不要、F/8をかける距離補正量Δρも不要となり、公式を省略できる。
function geosailing(lA,LA,lB,LB) {
//緯度経度をラジアンに変換
var latA = lA * (Math.PI/180);
var lngA = LA * (Math.PI/180);
var latB = lB * (Math.PI/180);
var lngB = LB * (Math.PI/180);
//化成緯度(Φ)
var phiA = Math.atan(Math.tan(latA));
var phiB = Math.atan(Math.tan(latB));
//球面上の距離(X)
var X = Math.acos(Math.sin(phiA) * Math.sin(phiB) + Math.cos(phiA) * Math.cos(phiB) * Math.cos(lngA-lngB)) * 6371.008;
return X;
}
ついでにラジアン変換を数式に代入、後方の*A/1000も6371008/1000=6371.008なので*6371.008に省略。
function geosailing(latA,lngA,latB,lngB) {
//化成緯度(Φ)
var phiA = Math.atan(Math.tan(latA*(Math.PI/180)));
var phiB = Math.atan(Math.tan(latB*(Math.PI/180)));
//球面上の距離(X)
var X = Math.acos(Math.sin(phiA) * Math.sin(phiB) + Math.cos(phiA) * Math.cos(phiB) * Math.cos(lngA*(Math.PI/180) - lngB*(Math.PI/180))) * 6371.008;
return X;
}
これだけでもかなり短くなった印象。
更に化成緯度Φを求める式も代入すれば(長いけど)距離計算が1つの数式に収まった。
function geosailing(latA,lngA,latB,lngB) {
var X = Math.acos(
Math.sin(Math.atan(Math.tan(latA*(Math.PI/180))))
* Math.sin(Math.atan(Math.tan(latB*(Math.PI/180))))
+ Math.cos(Math.atan(Math.tan(latA*(Math.PI/180))))
* Math.cos(Math.atan(Math.tan(latB*(Math.PI/180))))
* Math.cos(lngA*(Math.PI/180)-lngB*(Math.PI/180)))
* 6371.008;
return X;
}
さあ、もっと短く!
with文
withを使ってMath.を省略。
function geosailing(latA,lngA,latB,lngB) {
with(Math){
var X = acos(
sin(atan(tan(latA*(PI/180))))
*sin(atan(tan(latB*(PI/180))))
+cos(atan(tan(latA*(PI/180))))
*cos(atan(tan(latB*(PI/180))))
*cos(lngA*(PI/180)-lngB*(PI/180)))
*6371.008;
}
return X;
}
まだまだ、もっと短く!!
arctan(tan x)=x
三角関数を変形して数式を整理(この辺でワンライナー意識)。
function geosailing(latA,lngA,latB,lngB) {
with(Math){var X = acos(sin(latA*(PI/180))*sin(latB*(PI/180))+cos(latA*(PI/180))*cos(latB*(PI/180))*cos(lngA*(PI/180)-lngB*(PI/180)))*6371.008;}
return X;
}
もっとだ、もっと短く!!!
そして1行に
仕上げに引数の文字数を減らし、余計な()を外し、1行なのでwith文の{}を省略、セミコロンも省略、最後にreturn Xをまとめて完成。
function geosailing(a,b,c,d){
with(Math)return acos(sin(a*PI/180)*sin(c*PI/180)+cos(a*PI/180)*cos(c*PI/180)*cos(b*PI/180-d*PI/180))*6371.008
}
1行、110文字(スペース込み)で書けた^^)b
三角関数の理解が甘いので、もしかしたらもっと省略できるのかも?
追記
@il9437 様よりアドバイスいただきました。
//この位置で代入すれば一応詰め込むことはできます。
function geosailing(a,b,c,d){
with(Math)return acos(sin(a*(i=PI/180))*sin(c*i)+cos(a*i)*cos(c*i)*cos(b*i-d*i))*6371.008
}
89文字!
このタイミングで変数定義できるのかぁ。めっちゃ勉強になります(-人-)
更に @amenboakainaaiueo 様より!
//全然本質的なところではありませんが、2文字短くなりました(可読性は悪いですが)。
function geosailing(a,b,c,d){
with(Math)return acos(sin(a*=(i=PI/180))*sin(c*=i)+cos(a)*cos(c)*cos(b*i-d*i)*6371.008
}
86文字!
知識不足につきググりました。乗算代入というテクニックφ(・ω・ )フムフム...
実際に計算
2点の緯度経度をGoogleMapの「この場所について」で取得。GoogleMap上での距離測定と、GASでの距離計算を比較してみる。
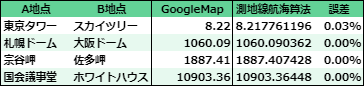
桁を揃えれば誤差なし╭( ・ㅂ・)و ̑̑ グッ !
結論
扁平率がゼロ(のGoogleMap)なら、緯度経度から2点間の距離を1行で求められる!