はじめに

こんにちは、やっしです。
この記事はTechCommit AdventCalendar2022の12日目の記事です。

概要

なにか物事を決める際などに、みなさんも１度はあみだくじを使ってことがあるかと思います。私もあみだくじはWebにあるやつを使ったりするのですが、自分好みに作ってみたいと思いあみだくじアプリを作成してみました。
本記事では、作成したあみだくじアプリを紹介するともに、そのシステム構成、そしてあみだくじを支える数学について述べます。

そもそもあみだくじって？
1. あみだくじのおさらい
2. あみだくじは非常によく出来ている
作成したアプリ
システム構成
数学の基礎
躓いたところ
1. nginxのウェルカムページが表示される
2. コンテナ間どうしの通信ができない
最後に
参考資料

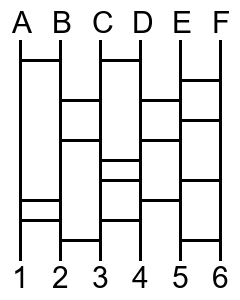
そもそもあみだくじって？

あみだくじのおさらい

数学的に言うなら、同じ数の入力データと出力データを一対一に対応させるもの、でしょうか。

念の為あみだくじについておさらいすると、
https://ja.wikipedia.org/wiki/%E3%81%82%E3%81%BF%E3%81%A0%E3%81%8F%E3%81%98

あみだくじ（阿弥陀籤）とは、線のはしに当たりはずれなどを書いて隠し、各自が引き当てるくじのこと。現在は、平行線の間に横線を入れ、はしご状にすることが多い。

こういうやつですね。あみだくじの良いところって、結局は運であるとわかっていながらも、くじ引きなどとは違い自分が引いた線で結果が良くも悪くも転がる可能性があって、ゲームに参加している感がより一層強くなるところだと思うんですよね。あとルールもシンプルですし、人数分の縦棒を書いたら、あとは適当に横線を引けば良いので準備もあっという間に終わります。

あみだくじは非常によく出来ている

そんなシンプルなあみだくじですが、とてもよくできていると思いませんか？
どのように横線を引いたとしても、入力はすべての出力に漏れなく重複無く対応する。
Aさん、Bさんの行き先が同じになることはないし、出力の「6」が誰にも対応しないということも起きないのです。
これがすごく重要な性質です。

作成したアプリ

URL（コスト削減により、一時的に非公開にしております。ご了承ください。）
http://ec2-13-231-247-107.ap-northeast-1.compute.amazonaws.com/amidakuji

デモ

システム構成

フロントエンド： React
バックエンド： Laravel

LaraveをAPIにして、Reactからaxiosでデータを送受信する形です。
ReactからLaravelに送信するデータは以下のような感じです。

{
    "amidas": [
        [
            false,
            false,
            false
        ],
        [
            true,
            false,
            false
        ],
        [
            false,
            false,
            false
        ],
        [
            false,
            false,
            false
        ]
    ]
}

trueは横線が入っていることを表し、amidasの第一階層目はあみだくじの行を表しており、第２階層目（booleanが入っているところ）は列を表します。この例の場合は、あみだくじの２行目の1列（１本目から2本目の間）に横線が入っていることを表しています。下記のamidasが、横線をクリックしたときや、本数を増減したときに更新されて、APIのパラメータとして送られます。

Amidakuji.jsx

    /**
     * あみだくじ
     */
    const [amidas, setAmidas] = useState(getInitialAmidas);

    /**
     * API通信
     */
    const updateResult = () => {
        axios
            .post('api/symmetric-group', {
                amidas: amidas,
            })
            .then(response => {
                setResults(response.data.data);
            })
            .catch(() => {
                console.log('通信に失敗しました');
            });
    }

バックエンド側の処理は、まずControllerに入り、バリデーションを行ってから、UseCaseの中に入ります。

SymmetricGroupController.php

<?php

namespace App\Http\Controllers;

use App\Http\Requests\SymmetricGroupRequest;
use App\Http\Response\SymmetricGroupResponse;
use App\Http\UseCase\AmidaUseCase;

class SymmetricGroupController extends Controller
{
    public function index(SymmetricGroupRequest $request): SymmetricGroupResponse
    {
        if ($request->isValidationFailed()) {
            return SymmetricGroupResponse::newInstanceFromInvalidRequest($request);
        }

        $amida_use_case = AmidaUseCase::newInstanceFromSymmetricGroupRequest($request);

        return SymmetricGroupResponse::newInstanceFromAmidaUseCase($amida_use_case);
    }
}

バリデーションの中身。
ちなみにLaravelでネストした配列データのバリデーションルールは以下のように書くことができます。

SymmetricGroupRequest.php

<?php

namespace App\Http\Requests;

class SymmetricGroupRequest extends ApiRequest
{
    /**
     * Determine if the user is authorized to make this request.
     *
     * @return bool
     */
    public function authorize()
    {
        return true;
    }

    /**
     * Get the validation rules that apply to the request.
     *
     * @return array<string, mixed>
     */
    public function rules(): array
    {
        return [
            'amidas' => [
                // amidas
                'required',
                'array',
            ],
            'amidas.*' => [
                // amidasの要素
                'required',
                'array',
            ],
            'amidas.*.*' => [
                // amidasの要素（配列）の要素
                'required',
                'bool',
            ],
        ];
    }

    /**
     * Get message when fail valiation
     *
     * @return array
     */
    public function messages(): array
    {
        return [
            'amidas.*' => 'amidasには配列を入れてください。',
            'amidas.*.*' => 'amidasの中は配列を入れてください。',
            'amidas.*.*.*' => 'amidasの中の配列の中にはbool値を入れてください。',
        ];
    }

    /**
     * バリデーションが失敗したかどうか
     *
     * @return boolean
     */
    public function isValidationFailed(): bool
    {
        return $this->validator->fails();
    }


    public function getValidationErrorMessages()
    {
        return $this->validator->errors()->messages();
    }
}

UseCaseの中身。
newInstanceFromSymmetricGroupRequestの中で、リクエストのbool値たちを「入力1を出力i_1に、入力2を出力i_2に、...」という情報に変換しています。

AmidaUseCase.php

<?php

namespace App\Http\UseCase;

use App\Http\Requests\SymmetricGroupRequest;
use App\Math\FundamentalTransposition;
use App\Math\SymmetricGroupMath;

class AmidaUseCase extends UseCase
{
    /**
     * constructor
     *
     * @param boolean $success
     */
    public function __construct(
        bool $successStatus = parent::SUCCESS,
        SymmetricGroupMath $responseData = null,
        string $errorMessage = ''
    )
    {
        parent::__construct(
            $successStatus,
            $responseData,
            $errorMessage
        );
    }

    /**
     * @param SymmetricGroupRequest $request
     * @return self
     */
    public static function newInstanceFromSymmetricGroupRequest(SymmetricGroupRequest $request): self
    {
        $dimension = count($request->amidas[0]) + 1;

        $accumulateSymmetricGroup = [];
        foreach ($request->amidas as $request_amida) {
            foreach ($request_amida as $index => $bool) {
                $accumulateSymmetricGroup[] = self::convertBoolToFundTrans($bool, $index, $dimension);
            }
        }

        return new self(
            parent::SUCCESS,
            SymmetricGroupMath::multiple_product(...$accumulateSymmetricGroup)
        );
    }

    /**
     * private
     */

    /**
     * @param boolean $bool
     * @return SymmetricGroupMath
     */
    private static function convertBoolToFundTrans(bool $bool, int $num, int $dimension): SymmetricGroupMath
    {
        return $bool
            ? new FundamentalTransposition($dimension, $num + 1)
            : SymmetricGroupMath::identity($dimension);
    }
}

もう少し詳しく見ていきましょう。convertBoolToFundTransは横線があれば（$boolがtrueなら）「*基本互換」を生成して、横線がなければ「*恒等写像」を返します。ちなみに先程から登場しているSymmetricGroupは「*置換群」という意味です。

基本互換、恒等写像などの数学用語が出てきました。これらは、あみだくじを支える「置換群」に関係するものです。ここで少し数学の基本的なことについて触れておきましょう。

数学の基礎

写像

ここまで登場してきたキーワードを理解するのに重要な概念が「写像」です。写像とは、入力に対して出力を1つ対応させる、そういったものです。写像を考える際、通常、入力が存在する集合と出力が存在する集合をセットで考えます。１つ例を考えてみましょう。
入力が存在する集合Xと出力が存在する集合Yがそれぞれ、1〜6までの自然数から成る集合で与えられるとします：

X = Y = \{1, 2, 3, 4, 5, 6\}

ここで、XからYへの写像fがXの元に対して、奇数なら1、偶数なら2を対応させるものである場合は

\begin{align}
f(1) &= f(3) = f(5) = 1 \\
f(2) &= f(4) = f(6) = 2
\end{align}

このようになります。次に紹介する「置換」は、写像にある制約を課したものになります。

置換

nを自然数としよう。1からnまでの数字からなる集合をA_nと置く：

A_n = \{1, 2, 3, \dots , n\}

ここで、A_nからそれ自身への写像σが漏れなくかつ重複なく対応する¹とき、その写像は （n文字の）置換 であるという。

\sigma : A_n \to A_n

例１）置換でない例
先程の「奇数を1、偶数を2に対応させる写像」

f : A_6 \to A_6

は、置換ではありません。

例２）置換である例
n = 5 として、次の3つ置換σ0、σ1、σ2を考えよう：

\begin{align}
\sigma_0(1) &= 2 \\
\sigma_0(2) &= 3 \\
\sigma_0(3) &= 4 \\
\sigma_0(4) &= 5 \\
\sigma_0(5) &= 1
\end{align}

\begin{align}
\sigma_1(1) &= 1 \\
\sigma_1(2) &= 3 \\
\sigma_1(3) &= 2 \\
\sigma_1(4) &= 4 \\
\sigma_1(5) &= 5
\end{align}

\begin{align}
\sigma_2(1) &= 1 \\
\sigma_2(2) &= 2 \\
\sigma_2(3) &= 3 \\
\sigma_2(4) &= 4 \\
\sigma_2(5) &= 5
\end{align}

σ0をあみだくじで表現すると次のとおりになる：

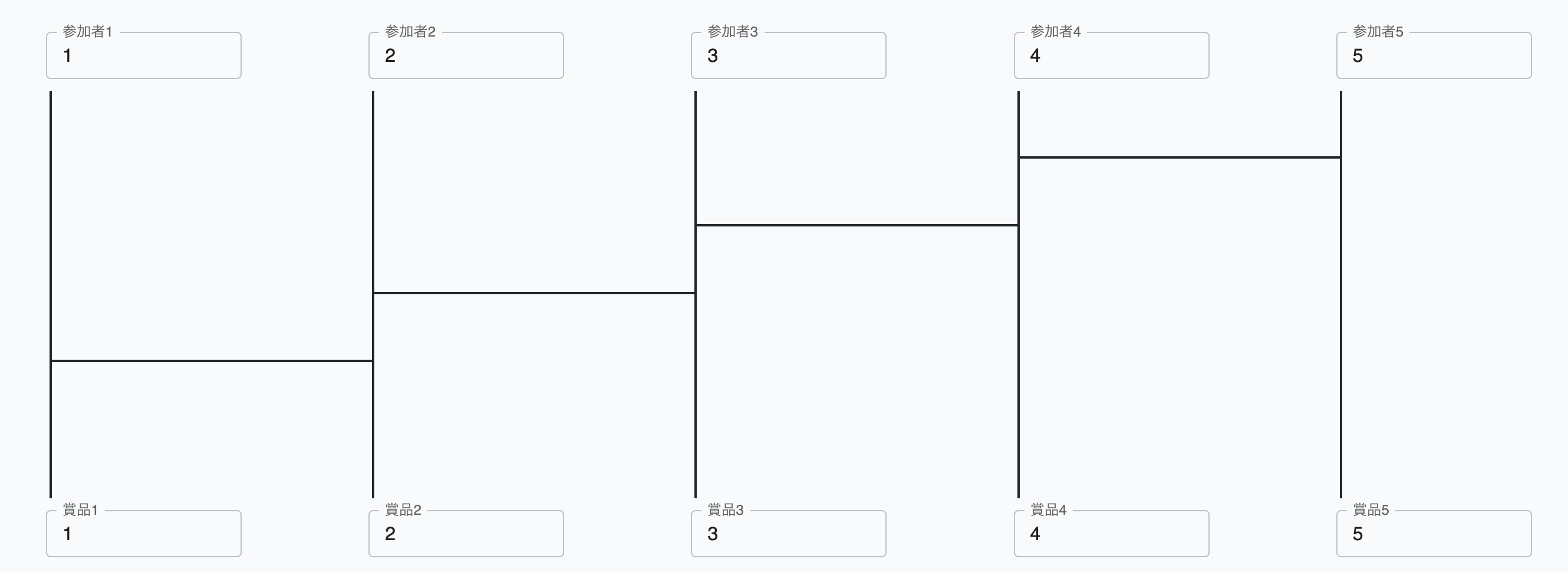
σ1のように、隣り合う数値を入れ替える置換を 「基本互換」 という。σ1をあみだくじで表現すると「2」と「3」の間に横線がただ1つ引かれたものである：

またσ2のように、入力と出力を変えないものを 「恒等写像」 という。

置換群（n次対称群）

「群」というのは、集合に積と呼ばれる２項演算が定義されていて、その演算の結果はまた集合に属するという性質を持ち、その積に関して結合法則が成り立ち、かつ単位元、逆元が存在するものである。

n文字の置換全体をS_nと置く：

S_n = \{ \sigma \: | \: \sigma : A_n \to A_n \text{ （全単射） } \}

このときS_nは合成写像を積として群となる。群であるから、置換同士の積もまた置換になるというのがとても扱いやすいポイントになっている。

例） n = 5 のとき上記のσ0とσ1の積を見てみよう。

\begin{align}
\sigma_0 \circ \sigma_1 : &\; A_n \xrightarrow{\sigma_1} A_n \xrightarrow{\sigma_0} A_n \\
&\; 1 \longrightarrow 1 \longrightarrow 2 \\
&\; 2 \longrightarrow 3 \longrightarrow 4 \\
&\; 3 \longrightarrow 2 \longrightarrow 3 \\
&\; 4 \longrightarrow 4 \longrightarrow 5 \\
&\; 5 \longrightarrow 4 \longrightarrow 1 \\
\end{align}

となって結局、積の結果は次のとおりになる。（前述の通りやはり置換（漏れなく、重複がない）である。）

\begin{align}
\sigma_0 \circ \sigma_1(1) &= 2 \\
\sigma_0 \circ \sigma_1(2) &= 4 \\
\sigma_0 \circ \sigma_1(3) &= 3 \\
\sigma_0 \circ \sigma_1(4) &= 5 \\
\sigma_0 \circ \sigma_1(5) &= 1
\end{align}

再掲

先程のコードの続きを見ていこう。

AmidaUseCase.php

<?php

namespace App\Http\UseCase;

use App\Http\Requests\SymmetricGroupRequest;
use App\Math\FundamentalTransposition;
use App\Math\SymmetricGroupMath;

class AmidaUseCase extends UseCase
{
...

    /**
     * @param SymmetricGroupRequest $request
     * @return self
     */
    public static function newInstanceFromSymmetricGroupRequest(SymmetricGroupRequest $request): self
    {
        $dimension = count($request->amidas[0]) + 1;

        $accumulateSymmetricGroup = [];
        foreach ($request->amidas as $request_amida) {
            foreach ($request_amida as $index => $bool) {
                $accumulateSymmetricGroup[] = self::convertBoolToFundTrans($bool, $index, $dimension);
            }
        }

        return new self(
            parent::SUCCESS,
            SymmetricGroupMath::multiple_product(...$accumulateSymmetricGroup)
        );
    }

    /**
     * private
     */

    /**
     * @param boolean $bool
     * @return SymmetricGroupMath
     */
    private static function convertBoolToFundTrans(bool $bool, int $num, int $dimension): SymmetricGroupMath
    {
        return $bool
            ? new FundamentalTransposition($dimension, $num + 1)
            : SymmetricGroupMath::identity($dimension);
    }
}

$accumulateSymmetricGroup で配列に集めているのは、基本互換である。そしてその基本互換たちをmultiple_productに入れてそれらの積を算出している。この積が、あみだくじを表現する置換になる。

おまけ（SymmetricGroupMathの中身）

SymmetricGroupMath.php

<?php

namespace App\Math;

use Exception;

class SymmetricGroupMath extends Math
{
    /**
     * 次元
     *
     * @var integer
     */
    protected int $dimension;

    /**
     * 置換を構成する写像
     *
     * @var array
     */
    protected array $map;

    /**
     * constructor
     */
    public function __construct(array $map)
    {
        $this->setDimension(count($map));
        $this->setMap($map);
    }

    /**
     * Getter
     */

    /**
     * get Dimension
     *
     * @return integer
     */
    public function getDimension(): int
    {
        return $this->dimension;
    }

    /**
     * get Map
     *
     * @return array
     */
    public function getMap(): array
    {
        return $this->map;
    }

    /**
     * Setter
     */

    /**
     * set Dimension
     *
     * @param int $dimension
     */
    protected function setDimension(int $dimension)
    {
        $this->dimension = $dimension;
    }

    /**
     * set Map
     *
     * @param array $map
     */
    public function setMap(array $map)
    {
        if (count(array_unique($map)) !== $this->dimension) {
            throw new Exception('置換のサイズが不適か、または重複した値が入っています。');
        }
        foreach ($map as $value) {
            if (!(is_int($value) && $value >= 1 && $value <= $this->dimension)) {
                throw new Exception('置換の文字は数字で、かつその数値は1からdimensionの間である必要があります。');
            }
        }
        $this->map = $this->key_inc($map);
    }

    /**
     * $perm_a * $perm_bを返す
     *
     * @param self $perm_a
     * @param self $perm_b
     * @return self
     */
    public static function product(self $perm_a, self $perm_b): self
    {
        if ($perm_a->dimension !== $perm_b->dimension) {
            throw new Exception('置換同士の積は、互いに同じ次元である必要があります。');
        }
        $map_a = $perm_a->map;
        $map_b = $perm_b->map;

        $producted_map = array_map(
            function($value) use($map_b) {
                return $map_b[$value];
            },
            $map_a
        );
        return new self($producted_map);
    }

    /**
     * 渡されたすべての置換の積を返す
     *
     * @param self ...$perms
     * @return self
     */
    public static function multiple_product(self ...$perms): self
    {
        return array_reduce(
            $perms,
            function ($accumulator, $element) {
                return self::product($accumulator, $element);
            },
            self::identity($perms[0]->dimension)
        );
    }

    /**
     * $permの逆元を返す
     *
     * @param self $perm
     * @return self
     */
    public function inverse(): self
    {
        $tmp_array =
        $invers_map = [];
        foreach ($this->map as $key => $value) {
            $tmp_array[$value] = $key;
        }
        for ($i = 1; $i <= count($this->map); $i++) {
            $invers_map[$i] = $tmp_array[$i];
        }
        return new self($invers_map);
    }

    /**
     * 恒等写像を返す
     *
     * @return self
     */
    public static function identity(int $dimension): self
    {
        $map = [];
        for ($i = 1; $i <= $dimension; $i++) {
            $map[$i] = $i;
        }

        return new self($map);
    }

    /**
     * private
     */

    /**
     * 配列のキーを1から振り直す
     *
     * @param array $map
     */
    private function key_inc(array $map)
    {
        $tmp_array = [];
        $count = 1;
        foreach ($map as $value) {
            $tmp_array[$count] = $value;
            $count++;
        }
        return $tmp_array;
    }
}

躓いたところ

ECSにデプロイするところでつまづきました。
デプロイの流れとしては、

ローカルでappコンテナ（php-fpm）とwebコンテナ（nginx）のDockerイメージを作成
ECRにそれぞれのDockerイメージをpush
ECSのタスク定義にそれぞれのコンテナを追加。
ECSサービス、クラスターを作成してタスクを起動（起動タイプはFargate、ネットワークモードはawsvpc）

nginxのウェルカムページが表示される

これ、さきに原因を言うと「Dockerイメージにソースコードが入っていない状態だった」んですよ。
ローカルではdocker-compose.ymlでマウント機能を使ってコンテナにホストのソースコードをコピーしていたので、Dockerコンテナにソースコードが入っている状態でした。
しかし、ECRにpushしたDockerイメージはDockerfileの記述に従って生成されるので、もしその中でホストのソースコードをコンテナにコピーする命令（COPYやADD）がなければDockerイメージは空の状態というわけです。（私の場合はnginxの設定ファイルのみCOPYしていたので、nginxのデフォルトページが表示されていたのだと思います。）

コンテナ間どうしの通信ができない

DockerイメージをECRにpushまで完了して、ECSタスクを起動したときすぐにタスクが落ちてしまいました。webコンテナのログを見ると

host not found in upstream "app" in /etc/nginx/conf.d/default.conf:23
[emerg] host not found in upstream "app" in /etc/nginx/conf.d/default.conf:23

appってホストが無い、とあります。nginxの中身をみると、

infra/nginx/default.conf

server {
    listen 80 default_server;
    root /data/public;

    add_header X-Frame-Options "SAMEORIGIN";
    add_header X-XSS-Protection "1; mode=block";
    add_header X-Content-Type-Options "nosniff";

    index index.php;

    charset utf-8;

    location / {
        try_files $uri $uri/ /index.php?$query_string;
    }

    location = /favicon.ico { access_log off; log_not_found off; }
    location = /robots.txt  { access_log off; log_not_found off; }

    error_page 404 /index.php;

    location ~ \.php$ {
        fastcgi_pass app:9000; # ← ここ
        fastcgi_param SCRIPT_FILENAME $realpath_root$fastcgi_script_name;
        include fastcgi_params;
    }

    location ~ /\.(?!well-known).* {
        deny all;
    }
}

該当の箇所では

fastcgi_pass app:9000;

となっています。ここでwebコンテナ（nginx）がappコンテナと通信する手段を記述しています。appはコンテナ名で、ちなみに9000はphp-fpmのデフォルトの待受ポートです。

$ man php-fpm

...（略）

DESCRIPTION

...（略）

       Most options are set in the configuration file. The configuration file is /usr/local/etc/php/7.4/php-fpm.conf.
       By default, php-fpm will respond to CGI requests listening on localhost  http  port  9000.  Therefore  php-fpm
       expects  your  webserver  to  forward all requests for '.php' files to port 9000 and you should edit your web-
       server configuration file appropriately.

ローカルでは各コンテナはコンテナ名を通じて通信できるのですが、なぜECSの中では認識できないのかめちゃくちゃハマりました。

単純に指定するhostの名称が間違っているか、起動順序（hostの名称はあっているが、appコンテナの前にwebコンテナが起動されてしまい、webコンテナがappコンテナを認識できていない）の問題か、この2つを考えました。

起動順序の問題が怪しそうだったので、ECSタスク定義内のwebコンテナのスタートアップ順序で、appコンテナがSTARTしたタイミングで起動するように設定して、再度ECSを起動してみました。

が、しかし表示されるログは変わりません。

1から設定を見直していると、ネットワークモードのawsvpcの考慮事項について、下記記事の中に次のような記述を見つけました：

awsvpc ネットワークモードを使用してタスクが開始されると、タスク定義内のコンテナが開始される前に、各タスクに Amazon ECS コンテナエージェントによって追加の pause コンテナが作成されます。次に、amazon-ecs-cni-plugins CNI プラグインを実行して pause コンテナのネットワーク名前空間が設定されます。その後、エージェントによってタスク内の残りのコンテナが開始されます。こうすることで pause コンテナのネットワークスタックが共有されます。つまり、タスク内のすべてのコンテナは ENI の IP アドレスによってアドレス可能であり、localhost インターフェイス経由で相互に通信できます。

「localhost インターフェイス経由で相互に通信できます。」
なので、該当の箇所を次のように修正して再度アップしました。

fastcgi_pass localhost:9000;

これでようやくECSが起動しました！

最後に

数学って面白いなと思ってもらえると、嬉しいです。
~~記事執筆中に、このアプリをデプロイ出来なかったのが残念ですが、でき次第アップしたいと思います！~~（追記：2022年12月18日、デプロイできましたー）
（追記：2023年1月1日、CIにも対応しました。インフラ周りの構成については、別の記事で書く予定です！）

それでは、13日目の記事もお楽しみに！

参考資料

このとき、その写像は「全単射」であるという。重複がないことを「単射」、漏れがないことを「全射」という。 ↩

あみだくじアプリを作ってみた