TL;DR
カルノー図(Karnaugh map)は論理回路の単純化などに用いる論理式の単純化方法です。
上手くいけば、こんな複雑なif文を
if ( is_admin and not is_correct_pw ) or ( not is_admin and not is_correct_pw ) or (not is_admin and is_correct_pw):
input_admin_pw()
こんなにシンプルで等価なif文に変換できます。
if not ( is_admin and is_correct_pw):
input_admin_pw()
使用できるのは基本的に4変数までです。
カルノー図
ざっくり行ってしまえば、式の出力を表にまとめたものです。
https://ja.wikipedia.org/wiki/カルノー図
変数の数によって、式の出力を入れる枡目の数が変わります。
| 変数の個数 | 枡目の数 |
|---|---|
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
変数が一つ増えれば、True or False の組み合わせの数も
2倍になる事を覚えておくと良いと思います。
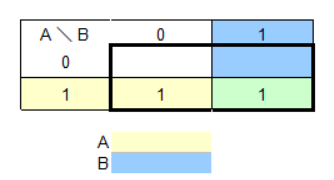
2変数
黄色の部分は変数AがTrueの部分、青色の部分は変数BがTrueの部分を示しています。
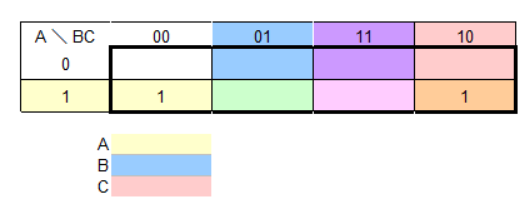
3変数
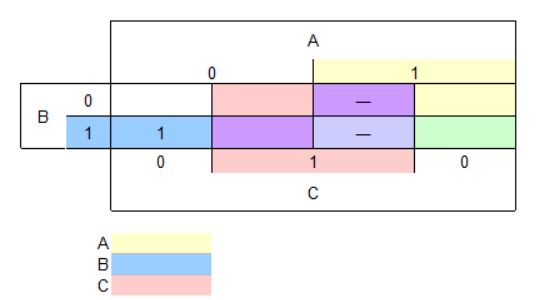
4変数
ベイチ図
基本はカルノー図と似たようなもので、書き方だけ違います。
2変数
3変数
Cが下に追加されます。
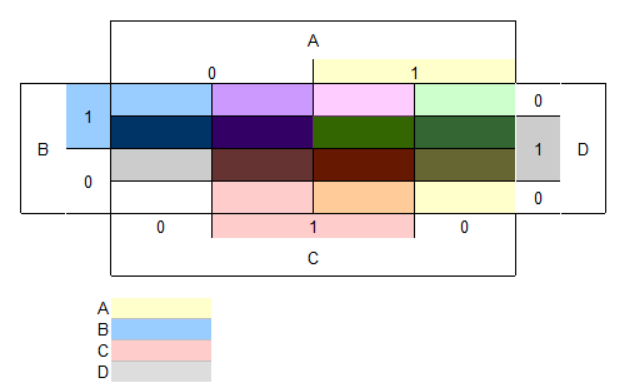
4変数
Dが右に追加されます。
使い方
@kawasima さんの エスイーが要件定義でやるべきたったひとつのこと(実践編) で
カルノー図を使用した方法が既に紹介されていますが、
こちらではもう少しかみ砕いて説明していきます。
また、ここではカルノー図ではなく代わりにベイチ図を使用します。
少し書き方は変わりますが、やることは変わりません。
基本的な使い方
以下の例を考えます。
if ( is_admin and not is_correct_pw ) or ( not is_admin and not is_correct_pw ) or (not is_admin and is_correct_pw):
input_admin_pw()
まずは、以下の様なベイチ図を作ります。
ここに、if文の条件がtrue となる箇所に順番に1を打っていきます。
先に真理値表の作成を行い、そこからベイチ図に書いても良いかもしれません。
まずは一つ目の括弧の中、 ( is_admin and not is_correct_pw ) に相当する箇所
続いて、or の後ろにある (not is_admin and not is_correct_pw) に相当する箇所
仕上げに、最後の括弧の (not is_admin and is_correct_pw) に相当する箇所
これにて、ベイチ図が示す条件はif文と同じになりました。
まずは、1がある箇所に着目してみます。
1がある領域は is_admin がFalse時の領域と is_correct_pw がFalseの時の領域の和になっています。
ここから、最初のコードは以下のコードと等価である事が分かります。
if ( not is_admin ) or ( not is_correct_pw ):
input_admin_pw()
もう一つ、0がある箇所に着目する方法があります。
is_admin と is_correct_pw が両方とも True の場合だけ 結果がFalseになるので、
こう置き換えられます。
if not ( is_admin and is_correct_pw):
input_admin_pw()
こちらについては、先ほどの条件からド・モルガンの法則で導き出せますね。
https://ja.wikipedia.org/wiki/ド・モルガンの法則
Early Returnがある場合
以下の様に、目的のif文の前にEarly Returnがある場合を考えます。
# Early Return
if is_ios and is_x86:
return
# ここのif文を単純化したい
if (is_chrome and is_x86) or (not is_chrome and is_x86 and not is_osx):
draw_warning()
何はともあれ、まずはベイチ図を作ります。
次に、以下のEarly Returnについて考えます。
if is_ios and is_x86:
return
これにより対象のif文に入ってこないため、"Don't care"を表す － をベイチ図に記します。
続いて対象のif文の最初の括弧 is_chrome and is_x86 の部分に1を打ちます。
なお、is_chrome, is_osx, is_x86全てTrueとなる箇所も該当しますが、
ここは既に － が入っており、1で上書きすると簡単化の障害になります。
そのため、 － のままにします。
そして、 or の後ろの括弧の中 not is_chrome and is_x86 and not is_osx の部分。
最後に、1の部分を括ります。このとき－ の箇所はどちらでも良いため
以下の様に領域を大きく取れます。
ここから、先ほどの処理は以下と同等だと言えます。
# Early Return (そのまま)
if is_ios and is_x86:
return
# 単純化したif文
if is_x86:
draw_warning()
5変数以上に使いたい場合
5変数の場合、平面のカルノー図/ベイチ図では表現しきれないため立体化します。
作図が難しいので、詳細は「カルノー図 5変数の場合」で検索してみてください。
また、クワイン・マクラスキー法を使う方法もあります。
https://ja.wikipedia.org/wiki/クワイン・マクラスキー法
・・・が、if文がなぜその条件になっているか
レビュー者に説明するのが大変という難点があります。
素直に判定関数を分割したり、Early Returnを行うことで、
そのif文で判定する変数を減らした方が良さそうです。