0. はじめに
抜取検査の統計的な意味を理解する上で確率分布の理解は欠かせません。品質管理の本にのってる計数値に関する確率分布を見ることで統計的な意味の理解はできますが、身近な検査事例について自分で確率分布を書きアウトプットしながら理解することはより効果的です。ただ、手書きで確率分布を描くことは大変ですしエクセルであっても少し面倒です。
Pythonの統計関数モジュールscipy.statsは簡単に確率分布を描画できるため、グラフをかく煩わしさがなく効率的に検査の意味を理解できます。この記事では、Python統計関数モジュールscipy.statsを使ったわかりやすい計数抜取検査の解説を目指します。
1. 抜取検査と二項分布
抜取検査は、保証すべき単位(母集団)から一定数のサンプル(標本)だけを抜き取り検査することです。検査結果に対してある判断基準で合格・不合格を決めるわけですが、全数検査ではないため同じ品質レベルであっても、サンプルによって合格になったり不合格になったりします。
統計を使えば、ある不良率の時にどのくらいの確率で合格になるのか、どれくらいのサンプル数が適切なのかを設計することができます。それを理解するために、まずは基本となる二項分布について考えてみましょう。
合格品のネジ90本と不良品のネジ10本が入った袋があったとします。この中から10本を取り出す際に、1本ずつ取り出し取り出した後にそれを戻しよく混ぜ直します(復元抽出)。これを10回反復します。袋の中には合格品のネジ90本と不良品のネジ10本が、常に混ざった状態で入っているため、1回の取り出しで不良品のネジを取り出す確率Pは、
\begin{align}
P &= 10/100 \\
&= 0.1
\end{align}
となります。よって、取り出した10本の中にk個の不良品が含まれる確率は、
\begin{align}
P(k) &= \frac{10!}{k!(10-k)!} (0.1)^k(0.9)^{10-k} \\
\end{align}
となります。(0 ≦ k ≦ 10)
一般的な形で表した場合、不良率をp、独立したサンプリングをn回行った時に不良品がk個含まれる確率は以下であらわせます。
\begin{align}
P(k) &= \frac{n!}{k!(n-k)!} (p)^k(1-p)^{n-k} \\
\end{align}
このような反復試行で得られる離散型確率変数は二項分布となります。これにより不良率p、サンプリング数n、サンプリングの中の不良数kの関係がわかります。
Pythonを使って、二項分布を書き3つの関係についてみていきましょう。二項分布の描画には、以下の記事を参考にさせていただきました。
まず、ライブラリーを読み込みます。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
!pip install japanize-matplotlib
import japanize_matplotlib
1-1 サンプルに含まれる不良の数・・・不良率pとサンプリング数n 固定
# 不良率
p = 0.1
# ネジを取り出す回数(サンプリング回数)
n = 10
# 取り出す不良数
k = np.arange(0, 10) # array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# pmfで成功回数ごとの確率を計算
binom_pmf = stats.binom.pmf(k, n, p) # 不良数=0~9, サンプリング回数=10, 不良率=0.1
# 可視化
plt.plot(k, binom_pmf, 'bo',ms=8)
plt.vlines(k, 0, binom_pmf, colors='b', lw=3, alpha=0.5)
plt.xticks(k) # x軸目盛
plt.xlabel("不良の数", fontsize=13)
plt.ylabel("確率質量関数", fontsize=13)
plt.show()
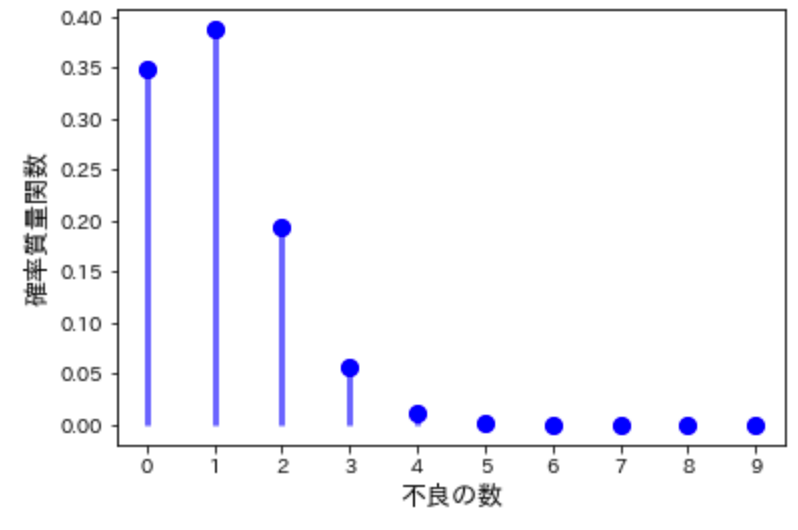
# 不良率P、サンプリングn回の時に、不良品がk個含まれる確率
stats.binom.pmf(k, n, p)
取り出した10本のネジの中に含まれる不良数の確率分布を描くことができました。約73.6%は0本もしくは1本であることがわかります。3本出る確率はグッと減って5.7%です。
1-2 不良率の確率密度関数・・・不良数kとサンプリング数n 固定
# x軸の等差数列を生成
p = np.linspace(start=0, stop=1, num=100)
# pmfで生存関数を生成
binom_sf = stats.binom.pmf(k=1, n=10, p=p)
# 可視化
plt.plot(p, binom_sf)
plt.xlabel("不良率P", fontsize=13)
plt.ylabel("確率密度関数", fontsize=13)
plt.show()

ここでは、サンプル数を10個それに含まれる不良数を1個と固定し、不良率pを変化させたときの確率を描いています。不良率0.1のあたりでピークとなっていることがわかります。それぞれの不良率で、サンプル数10個不良率1個が発生する確率をつかむことができます。
2. OC曲線
抜取検査では、保証すべき単位(以下ロット)からのサンプリング結果をもとにロットの合否を判定します。合否判定には、不良がc個以下の時に合格、c+1個以上の時に不合格といった判定基準を設定することとなります。
合格基準である不良c個以下の確率は、0個の時の確率、1個の時の確率とc個までの確率を累積していけばもとまります。式で書くと次のようになります。
\begin{align}
&P(≦c) = P(0)+P(1)+・・・ +P(c)&
\end{align}
では、この式を横軸を不良率、縦軸をロット合格率としてプロットしてみます。
2-1 不良率の累積分布関数・・・不良数kとサンプリング数n 固定
# x軸の等差数列を生成
p = np.linspace(start=0, stop=0.5, num=50)
# cdfで累積分布関数を生成
binom_sf = stats.binom.cdf(k=1, n=10, p=p, loc=0)
# 可視化
plt.plot(P, binom_sf)
plt.xlabel("不良率P", fontsize=13)
plt.ylabel("累積分布関数", fontsize=13)
plt.show()
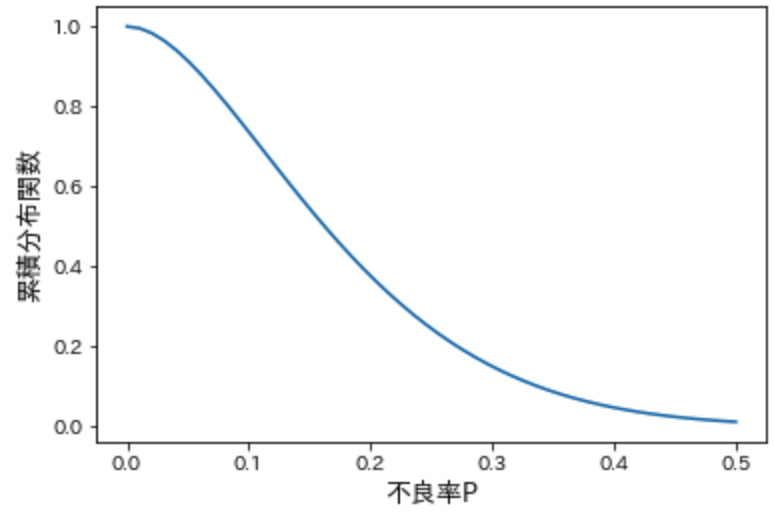
このようにロットの不良率に対してロットの合格確率をプロットした累積確率曲線をOC曲線(operating characteristic curve)といいます。上に示したOC曲線の場合、合格基準をサンプル10個中不良数1個以下とした時に、不良率によってどのくらい合格するかを表しています。具体的に不良率0.1の時の合格率をみてみます。下記の図では、わかりやすいように不良率0.1に垂直線と水平線を引きました。
2-2 OC曲線・・・不良数kとサンプリング数n 固定 垂直線・水平線・合格率表記あり
# x軸の等差数列を生成
p = np.linspace(start=0, stop=0.5, num=50)
# cdfで累積分布関数を生成
binom_sf = stats.binom.cdf(k=1, n=10, p=p, loc=0)
# 可視化
plt.plot(p, binom_sf)
# cdfで、k=1, n=10 確率を求める
pass_rate = stats.binom.cdf(k=1, n=10, p=0.1)
plt.plot(0.1, pass_rate, 'bo') # 青色ドット
plt.vlines(0.1, 0.0, pass_rate, lw=2, linestyles='dashed') # 垂直線
plt.hlines(pass_rate, 0, 0.1, lw=2, linestyles='dashed') # 水平線
plt.xlabel("不良率P", fontsize=13)
plt.ylabel("累積分布関数", fontsize=13)
plt.show()
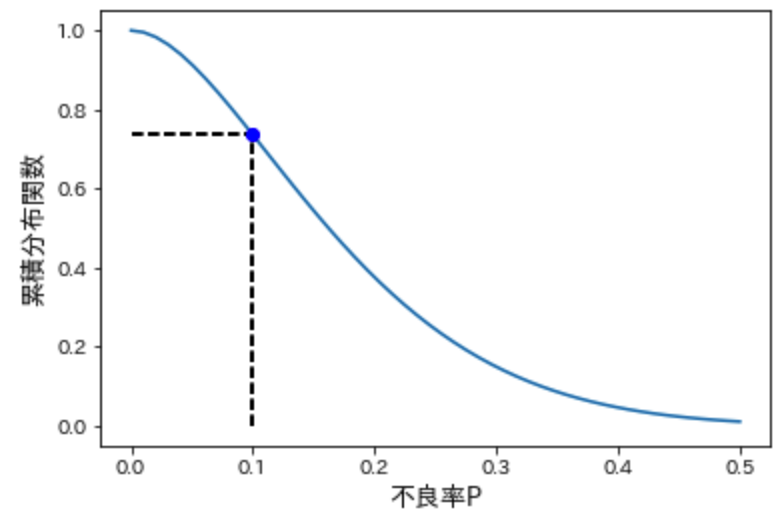
このように、不良率0.1の時の合格率は73.6%であることがわかります。
2-3 OC曲線・・・サンプリング数によるOC曲線の変化 n= 10, 15, 20, 25
サンプル数によってOC曲線はどう変わるかをみてみましょう。合格基準をサンプルn個中不良数1個以下とし、nを10, 15, 20, 25と変化させてみます。
# x軸の等差数列を生成
p = np.linspace(start=0, stop=0.6, num=50)
# cdfで累積分布関数を生成
for i in range(10, 30, 5):
binom_sf = stats.binom.cdf(k=1, n=i, p=p, loc=0)
plt.plot(P, binom_sf, label=f"n={i}")
plt.legend()
plt.xlabel("不良率P", fontsize=13)
plt.ylabel("累積分布関数", fontsize=13)
plt.show()
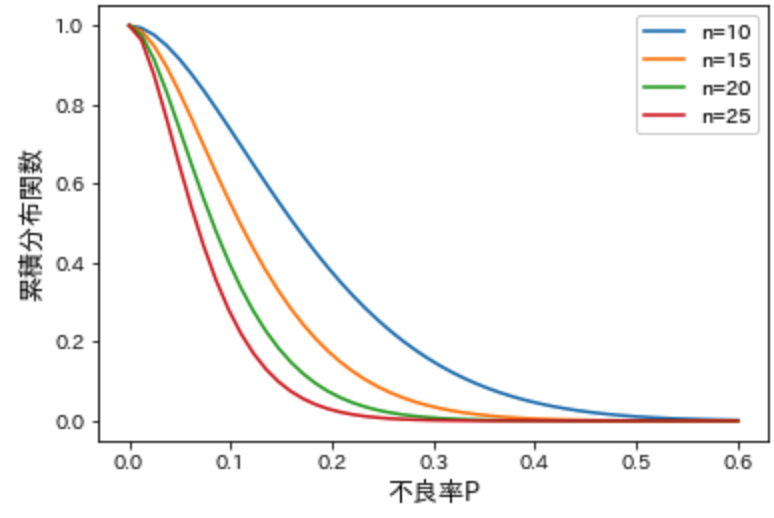
グラフからわかるように、nが増えるにつれて曲線が左へ移動していくことがわかります。不良率0.1の場合、n=10の時の合格率は73.6%でしたが、n=25では27.1%となります。サンプル数が増えたことでより正確に判定を行えるようになってくることがわかります。
3. 生産者危険と消費者危険
2-3で確認したように、サンプル数が増えると正確な検査を行うことができます。サンプル数をどんどん増やせば、最終的には全数検査となりサンプリングに起因する見逃しはなくなります。全数検査は確実な検査を行えますが、それだけ時間、人手、設備などが必要となってしまいます。製造現場では、抜取検査と全数検査を組み合わせて必要な品質を確保することとなります。
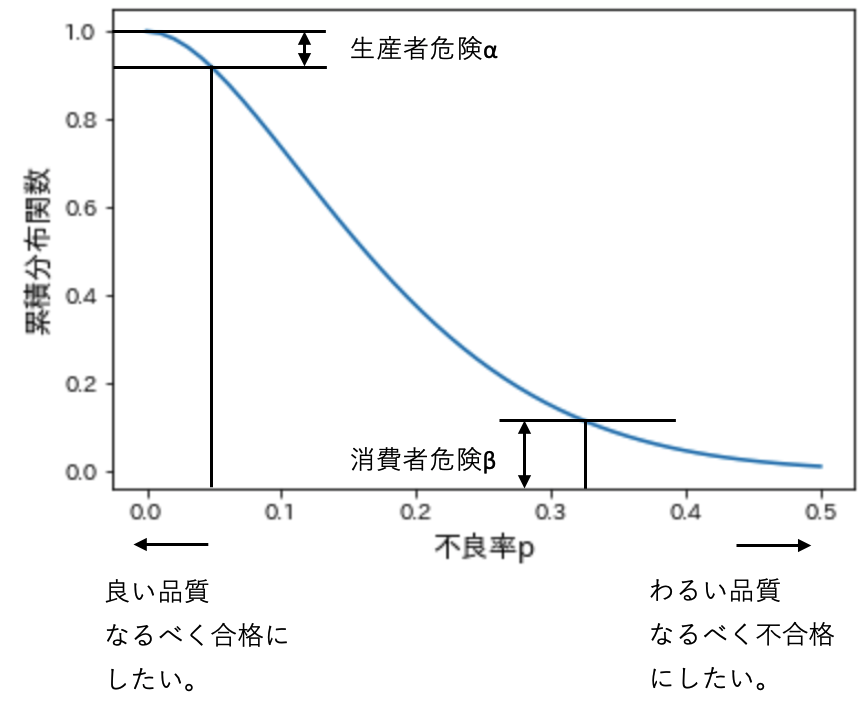
抜取検査をするさいに、サンプル数はどのように決めればいいのでしょうか。OC曲線では、曲線上の2点を決めることで生産者と消費者の両者に対しての品質保証状の取り決めをすることができます。下記の図において、αのロットの不良率は0に近く品質としては良いです。しかし、α分は不合格となってしまいます。このαを第1種の誤りといい、αが大きいと生産者が不利になるので生産者危険と言います。βのロットの不良率は高く品質としては悪いです。しかし、β分は合格となってしまいます。このベータを第2種の誤りと言い、βが大きいと消費者が不利になるので消費者危険と言います。一般的には、α = 5%、β = 10%でサンプル数を設計します。
4. おわりに
ここまで統計関数モジュールscipy.statsで描画したグラフを用いて説明してきました。計数抜取検査の統計的な感覚をつかむには、身近な抜取検査の条件を想定してグラフを書くと感覚が掴みやすいです。Pythonを使うと簡単にグラフ描画ができますので、計数抜取検査を理解する際には試してみてください。
参考文献
谷津 進、宮川 雅巳 著 (1988) 経営工学ライブラリー6 品質管理、朝倉書店
参考サイト
抜取検査とOC曲線