Cutmix はテーブルデータに対しても有効か？

初めに

通常，教師あり学習は，高精度を達成するため，十分な量のラベル付きデータを必要とします．しかし，人手による注釈は，非常に多くの時間と労力を要します．これを解決する方法の一つとして，人工的にデータをかさ増しするデータ拡張（data augmentation）があります．

しかし，データ拡張は，画像ありきに語られることがほとんどで，テーブルデータに適用できる手法は，そう多くありません．そこで，本記事は，テーブルデータに適用できるデータ拡張を紹介し，実験を行い，それらの性能を検証します．

Mixup

mixup: Beyond Empirical Risk Minimization

Mixup は，2017 年に提案された手法で，ICLR に採択されました．二つの入力を混ぜ合わせることで，新たな入力を生成します．

import random as rn

from sklearn.utils import check_random_state


def mixup(x, y=None, alpha=0.2, p=1.0, random_state=None):
    n, _ = x.shape

    if n is not None and rn.random() < p:
        random_state = check_random_state(random_state)
        l = random_state.beta(alpha, alpha)
        shuffle = random_state.choice(n, n, replace=False)

        x = l * x + (1.0 - l) * x[shuffle]

        if y is not None:
            y = l * y + (1.0 - l) * y[shuffle]

    return x, y

画像の他に，音声やテーブルデータに対して Mixup を適用しても性能が向上したことが論文中で報告されています．

Cutmix

CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features

Cutmix は，2019 年に提案された手法で，ICCV に採択されました．入力の一部分をもう一方の入力で置き換えることで，新たな入力を生成します．

import random as rn

import numpy as np
from sklearn.utils import check_random_state


def cutmix(x, y=None, alpha=1.0, p=1.0, random_state=None):
    n, h, w, _ = x.shape

    if n is not None and rn.random() < p:
        random_state = check_random_state(random_state)
        l = np.random.beta(alpha, alpha)
        r_h = int(h * np.sqrt(1.0 - l))
        r_w = int(w * np.sqrt(1.0 - l))
        x1 = np.random.randint(h - r_h)
        y1 = np.random.randint(w - r_w)
        x2 = x1 + r_h
        y2 = y1 + r_w
        shuffle = random_state.choice(n, n, replace=False)

        x[:, x1:x2, y1:y2] = x[shuffle, x1:x2, y1:y2]

        if y is not None:
            y = l * y + (1.0 - l) * y[shuffle]

    return x, y

Cutmix は，画像に対して適用した結果しか論文中で報告されていません．これを，テーブルデータに対して適用するとどうなるのでしょうか．

テーブルデータは，特徴（年齢や国籍等）の順序に意味がありません．そこで，もう一方の入力で置き換える部分を無作為に選ぶことにします．

import random as rn

import numpy as np
from sklearn.utils import check_random_state


def cutmix_for_tabular(x, y=None, alpha=1.0, p=1.0, random_state=None):
    n, d = x.shape

    if n is not None and rn.random() < p:
        random_state = check_random_state(random_state)
        l = random_state.beta(alpha, alpha)
        mask = random_state.choice([False, True], size=d, p=[l, 1.0 - l])
        mask = np.where(mask)[0]
        shuffle = random_state.choice(n, n, replace=False)

        x[:, mask] = x[shuffle, mask]

        if y is not None:
            y = l * y + (1.0 - l) * y[shuffle]

    return x, y

実験

今回は，次のデータセットを使って実験を行います．これは，遺伝子発現パターンから化合物の作用機序を予測するマルチラベル分類問題です．

Mechanisms of Action (MoA) Prediction | Kaggle

実験の詳細は，以下のコードを確認して下さい．

• moa-baseline | Kaggle
• moa-mixup | Kaggle
• moa-cutmix | Kaggle

Logloss は，次のようになりました.

	Local	Public	Private
Baseline	0.01604	0.01906	0.01666
Mixup	0.01605	0.01905	0.01668
Cutmix	0.01604	0.01901	0.01663

Public, Private 共に Cutmix でスコアが向上することを確認できました．

終わりに

Cutmix は，テーブルデータに対しても有効な手法です．

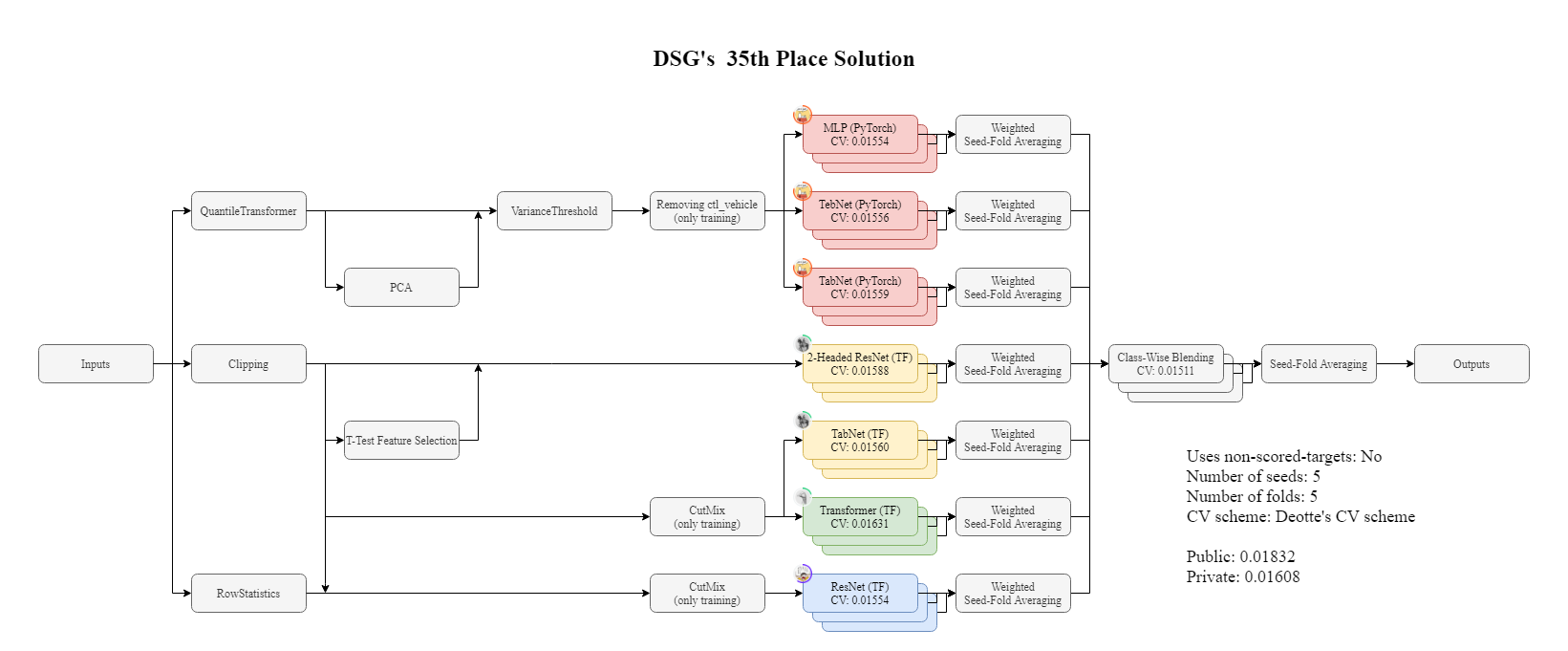
最後に，上記大会で Cutmix を用いて 35 位になった解法を公開しているので，興味のある方は，ご覧下さい．

Mechanisms of Action (MoA) Prediction | Kaggle