概要
ハフ(Hough)変換は、画像の中から直線や円などの図形を検出したい際によく用いられる手法の一つです。検出精度は高いですが、その分演算負荷が高く、またメモリも多く消費するなどの欠点があります。
しかし、理論が美しいことから、ぜひ覚えておきたい画像処理アルゴリズムの一つだと私は思いました。以下の記述は、次の記事を参考にしています。
Hough変換による画像からの直線や円の検出:CodeZine(コードジン)
そもそもハフ変換って何を変換してるの?
端的に言えば、座標系を変換しています。これだけでは何を言っているのかが分かりづらいと思いますので、2つの例で説明しましょう。
直線を検出したい場合
直線はパラメータが2つあれば表すことができます。数学の教科書での直線は「$y=ax+b$」とか「$ax+by+c=0$」とかが有名ですが、Hough変換的には「$ρ=xcosθ+ysinθ$」としてρとθで表すのが一般的です(aとbの組だと垂直・水平線が扱いづらいため)。図にするとこんな感じですね。
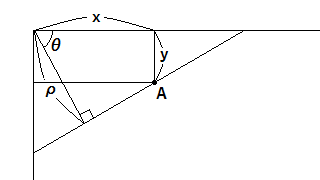
ここでA点は、ハフ変換する前の点でその座標は(x, y)と表されます。その点を通る直線は、図のようにρとθで表されます。ここで気づかれた方も多いと思いますが、A点を通るρとθの組は無数にあります。
……まぁ落ち付け。銃を突き付けられてはビビって話もできやしねぇ。A点という基準が1つ定まっているお陰で、「無数にある」と言っても1次元分だけ考えれば済みます。なぜなら、ρとθのどちらかを定めるともう一方は計算で出てきますから。図形の対称性からθは0≦θ<πの範囲だけ考えればいいですし、ρは元画像の対角線より長くなることはありませんので、ρとθの組は次の図のように平面上に曲線としてプロットできます。
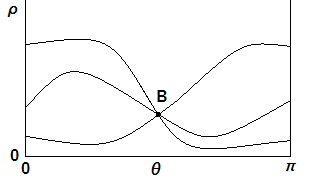
この曲線は当然、元画像に存在する点の数(ハフ変換で取り上げられる数)だけ存在します。それが多く交差した点(図における点B)とはつまり、元画像の複数点から強く予測されるρとθの組=求めたい直線に他なりません。交差点が複数存在する場合もありますが、それはつまり元画像に複数の直線が存在する(可能性が高い)ということですので問題ありません。かくして、元画像に潜む直線を見つけ出すことができました。
円を検出したい場合
円はパラメータが3つあれば表すことができます。ここは、数学の教科書に載っている「$(x-p)^2+(y-q)^2=r^2$」を使用することにします。中心が(p, q)で半径がrの円を考えるわけですね。下の図では、C点が(x, y)でD点が(p, q)となります。
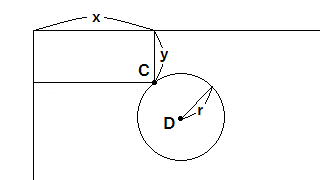
直線の場合はθを変化させたわけですが、今度はpとqを変化させることにします。三平方の定理からrを逆算できますので、直線の場合と同じく、元画像の全ての点に対して同じ作業を行うことで、多く交差した点(p, q, r)=求めたい円ということになります。この書き方でお分かりの通り、パラメータが3つあるとハフ変換後の空間は3次元になります。n個のパラメータで表せる図形ならn次元空間になりますね。
ハフ変換した後に何をするべきか
以上をプログラムとして記述すると、次のようになるでしょう。
- 元画像を読み込む
- 前処理を行う。基本的には、二値化した後にゴミを除去し、細線化処理を行うことが多い
- ハフ変換を行い、結果を配列などで取得する。パラメータ数が多いほど計算時間が加速度的に増加するので注意
- 多く交差した点を検索して取得する。そういった点は複数得られることもある
**「ね、簡単でしょう?」**と言いたいところですが、そんなわけないんですよね……。注意すべきポイントもまとめてみました。
- ハフ変換する範囲をよく考えること。計算量をケチりつつ精度の高い結果を得たいので、例えば直線ではθの範囲やその分割数、円では中心の座標(p, q)や半径rの範囲について事前に条件を確認しましょう。
- 量子化誤差を考慮すること。理論上は上記のように交点が綺麗に出てくるはずですが、実際には量子化誤差のせいである程度点がブレてしまいます。詳しくは後ほど解説しますが、そのせいで既に発見した交点の周りを無視するといった処理が必要になります。ただそうなると、似た感じの図形が並んでいた場合に検出できなくなったりするのでジレンマですが。
- 幾つまで取得するかを考えること。量子化誤差の話題にも繋がりますが、「上位10種類」や「しきい値未満なら無視する」などで篩に掛けないと大量の候補が検出されてしまいます。
実際のプログラム例
とりあえずJavaで実装しました。実行結果は次の画像をご覧ください。
処理前(640x360):http://i.imgur.com/0g3vWFT.png
ハフ変換後の領域(横軸がθ、縦軸がρ):http://i.imgur.com/TQbnDL7.png
ハフ変換後の領域(横軸がp、縦軸がq):http://i.imgur.com/VcgM9Y4.png
処理後(検出した図形を色付け):http://i.imgur.com/65QtNLJ.png
i7-4790K・Win10で実行したところ、画像出力時間を含めて2.4秒ほど掛かりました。まあ大部分が円を検出する際のハフ変換処理なので、パラメータが1つ増えるだけでいかに面倒かが分かりますね。
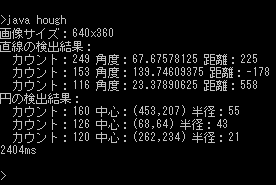
また、ハフ変換後の領域を見れば分かるように、明るい点の周りにモヤのようにほんのりと明るい点が続いていることが分かります。その明るい点すらも、隣接ピクセルは同じぐらい明るかったりするので前述のような篩掛けをしないと上手く検出できないと分かるでしょう。
以下にコードを載せますが、勉強する際はそのままコピペなんてせず自力で実装してみてください。より多くのパラメータを必要とする図形を検出してみても面白いかもしれません。
/* Hough変換のサンプル
* Hough変換した際は、
* 直線→横×縦が角度分割数×(2 * 対角線長)に対応する
* (ここで対角線長を2倍しているのは負数を想定している)
* 円→横×縦が横×縦×半径に対応する
*/
/* 引数の1つ目が「put」だったなら、counter*.pngを出力する */
import java.awt.Color;
import java.awt.Graphics2D;
import java.awt.image.BufferedImage;
import java.io.File;
import java.util.ArrayList;
import javax.imageio.ImageIO;
public class hough{
// 定数
static final int kAngleSplits = 1024; //0~πをこの数だけ分割する
static final int kMinCount = 100; //カウントがこの数未満なら無視する
static final int kMaxCircleR = 100; //円がこれ以上の大きさなら無視する
static final double kTableConst = Math.PI / kAngleSplits; //計算用定数
static final double kDegRad = 180 / Math.PI; //変換用定数
// 変数
static int w, h, diagonal, d2;
static ArrayList<Double> sin_table, cos_table;
static ArrayList<Integer> dgl_table;
// main関数
public static void main(String args[]){
boolean save_flg = false;
if(args.length > 0 && args[0].equals("put")) save_flg = true;
// 画像を読み込み
BufferedImage load_image;
try{
load_image = ImageIO.read(new File("sample.png"));
}
catch(Exception error){
error.printStackTrace();
return;
}
w = load_image.getWidth();
h = load_image.getHeight();
System.out.println("画像サイズ:" + w + "x" + h);
long start = System.nanoTime();
// 書き込み用画像を用意する
BufferedImage save_image = new BufferedImage(w, h, BufferedImage.TYPE_INT_BGR);
Graphics2D g2d = (Graphics2D)save_image.getGraphics();
g2d.drawImage(load_image, 0, 0, null);
// 二値化
ArrayList<Integer> binary_image = toBinaryImage(load_image);
// 数値計算用のテーブルを事前に用意する
sin_table = new ArrayList<Double>(kAngleSplits);
cos_table = new ArrayList<Double>(kAngleSplits);
for(int t = 0; t < kAngleSplits; t++){
sin_table.add(Math.sin(kTableConst * t));
cos_table.add(Math.cos(kTableConst * t));
}
dgl_table = new ArrayList<Integer>(w * h);
for(int y = 0; y < h; y++){
for(int x = 0; x < w; x++){
dgl_table.add((int)(Math.sqrt(x * x + y * y) + 0.5));
}
}
// 直線を検出する
ArrayList<Tuple2> line_list = calcHoughLine(binary_image, save_flg);
drawHoughLine(save_image, line_list);
// 円を検出する
ArrayList<Tuple3> circle_list = calcHoughCircle(binary_image, save_flg);
drawHoughCircle(save_image, circle_list);
// 結果を書き出し
long stop = System.nanoTime();
System.out.println((stop - start) / 1000 / 1000 + "ms");
try{
ImageIO.write(save_image, "png", new File("result.png"));
}
catch(Exception error){
error.printStackTrace();
return;
}
}
// 画像を二値化して返す
private static ArrayList<Integer> toBinaryImage(BufferedImage src_image){
ArrayList<Integer> dst_image = new ArrayList<Integer>(w * h);
for(int y = 0; y < h; y++){
for(int x = 0; x < w; x++){
int color = src_image.getRGB(x, y);
int r = (color & 0xff0000) >> 16;
int g = (color & 0xff00) >> 8;
int b = color & 0xff;
double Y = 0.299 * r + 0.587 * g + 0.114 * b; //YCbCr
if(Y > 127.5)
dst_image.add(0);
else
dst_image.add(1);
}
}
return dst_image;
}
// 画像をHough変換する(直線偏)
private static ArrayList<Integer> getHoughLine(ArrayList<Integer> src_image){
diagonal = (int)Math.sqrt(w * w + h * h);
d2 = diagonal * 2;
ArrayList<Integer> dst_image = new ArrayList<Integer>(kAngleSplits * d2);
for(int r = 0; r < d2; r++){
for(int t = 0; t < kAngleSplits; t++){
dst_image.add(0);
}
}
// 座標変換を行い、結果に加算しておく
for(int y = 0; y < h; y++){
for(int x = 0; x < w; x++){
if(src_image.get(y * w + x) == 0) continue;
for(int t = 0; t < kAngleSplits; t++){
int r = (int)(x * cos_table.get(t) + y * sin_table.get(t) + 0.5);
int p = (r + diagonal) * kAngleSplits + t;
dst_image.set(p, dst_image.get(p) + 1);
}
}
}
return dst_image;
}
// 直線を検出する
private static ArrayList<Tuple2> calcHoughLine(ArrayList<Integer> src_image, boolean save_flg){
ArrayList<Integer> counter = getHoughLine(src_image);
// カウントを画像化する
int max_count = 0;
if(save_flg){
BufferedImage counter_image = new BufferedImage(kAngleSplits, d2, BufferedImage.TYPE_INT_BGR);
for(int r = 0; r < d2; r++){
for(int t = 0; t < kAngleSplits; t++){
int cnt = counter.get(r * kAngleSplits + t);
if(max_count < cnt) max_count = cnt;
}
}
for(int r = 0; r < d2; r++){
for(int t = 0; t < kAngleSplits; t++){
int cnt = counter.get(r * kAngleSplits + t);
int color = (int)(255.0 * cnt / max_count);
counter_image.setRGB(t, r, color * 0x010101);
}
}
try{
ImageIO.write(counter_image, "png", new File("counter.png"));
}
catch(Exception error){
error.printStackTrace();
return null;
}
}
// 最もカウントが多いものから、直線として表示する
ArrayList<Tuple2> result = new ArrayList<Tuple2>();
System.out.println("直線の検出結果:");
while(true){
// 最もカウントが多いものを検索する
max_count = 0;
int t_max = 0, r_max = 0;
for(int r = 0; r < d2; r++){
for(int t = 0; t < kAngleSplits; t++){
int cnt = counter.get(r * kAngleSplits + t);
if(max_count < cnt){
max_count = cnt;
t_max = t;
r_max = r;
}
}
}
if(max_count < kMinCount) break;
result.add(new Tuple2<Integer, Integer>(t_max, r_max));
System.out.println(" カウント:" + max_count + " 角度:" + (t_max * kTableConst * kDegRad) + " 距離:" + (r_max - diagonal));
// 類似した周辺のカウントを消去する
for(int r = -10; r <= 10; r++){
for(int t = -30; t <= 30; t++){
int t2 = t_max + t, r2 = r_max + r;
if(t2 < 0){
t2 += kAngleSplits;
r2 = -r2;
}
if(t2 >= kAngleSplits){
t2 -= kAngleSplits;
r2 = -r2;
}
if(r2 < 0 || r2 >= d2) continue;
counter.set(r2 * kAngleSplits + t2, 0);
}
}
}
return result;
}
// 直線を書き出す
private static void drawHoughLine(BufferedImage image, ArrayList<Tuple2> list){
Graphics2D g2d = (Graphics2D)image.getGraphics();
g2d.setColor(Color.BLUE);
for(Tuple2<Integer, Integer> temp : list){
int t = temp.t1, r = temp.t2 - diagonal;
if(t != 0){
for(int x = 0; x < w; x++){
int y = (int)((r - x * cos_table.get(t)) / sin_table.get(t));
if(y < 0 || y >= h) continue;
g2d.drawRect(x, y, 0, 0);
}
}
if(t != kAngleSplits / 2){
for(int y = 0; y < h; y++){
int x = (int)((r - y * sin_table.get(t)) / cos_table.get(t));
if(x < 0 || x >= w) continue;
g2d.drawRect(x, y, 0, 0);
}
}
}
}
// 画像をHough変換する(円弧偏)
private static ArrayList<Integer> getHoughCircle(ArrayList<Integer> src_image){
ArrayList<Integer> dst_image = new ArrayList<Integer>(w * h * kMaxCircleR);
for(int x = 0; x < w; x++){
for(int y = 0; y < h; y++){
for(int r = 0; r < kMaxCircleR; r++){
dst_image.add(0);
}
}
}
// 座標変換を行い、結果に加算しておく
for(int y = 0; y < h; y++){
for(int x = 0; x < w; x++){
if(src_image.get(y * w + x) == 0) continue;
for(int cy = Math.max(y - kMaxCircleR, 0); cy <= Math.min(y + kMaxCircleR, h - 1); cy++){
int dy = Math.abs(cy - y);
for(int cx = Math.max(x - kMaxCircleR, 0); cx <= Math.min(x + kMaxCircleR, w - 1); cx++){
int dx = Math.abs(cx - x);
int r = dgl_table.get(dy * w + dx);
if(r >= kMaxCircleR) continue;
int p = (cy * w + cx) * kMaxCircleR + r;
dst_image.set(p, dst_image.get(p) + 1);
}
}
}
}
return dst_image;
}
// 円を検出する
private static ArrayList<Tuple3> calcHoughCircle(ArrayList<Integer> src_image, boolean save_flg){
ArrayList<Integer> counter = getHoughCircle(src_image);
// カウントを画像化する
int max_count = 0;
if(save_flg){
BufferedImage counter_image_c = new BufferedImage(w, h, BufferedImage.TYPE_INT_BGR);
BufferedImage counter_image_r = new BufferedImage(w, h, BufferedImage.TYPE_INT_BGR);
for(int y = 0; y < h; y++){
for(int x = 0; x < w; x++){
for(int r = 0; r < kMaxCircleR; r++){
int cnt = counter.get((y * w + x) * kMaxCircleR + r);
if(max_count < cnt) max_count = cnt;
}
}
}
for(int y = 0; y < h; y++){
for(int x = 0; x < w; x++){
int max_count_2 = 0, max_r = 0;
for(int r = 0; r < kMaxCircleR; r++){
int cnt = counter.get((y * w + x) * kMaxCircleR + r);
if(max_count_2 < cnt){
max_count_2 = cnt;
max_r = r;
}
}
counter_image_c.setRGB(x, y, 0x010101 * (int)(0xff * max_count_2 / max_count));
counter_image_r.setRGB(x, y, 0x010101 * (int)(0xff * max_r / kMaxCircleR));
}
}
try{
ImageIO.write(counter_image_c, "png", new File("counter2_c.png"));
ImageIO.write(counter_image_r, "png", new File("counter2_r.png"));
}
catch(Exception error){
error.printStackTrace();
return null;
}
}
// 最もカウントが多いものから、円として表示する
ArrayList<Tuple3> result = new ArrayList<Tuple3>();
System.out.println("円の検出結果:");
while(true){
// 最もカウントが多いものを検索する
max_count = 0;
int x_max = 0, y_max = 0, r_max = 0;
for(int y = 0; y < h; y++){
for(int x = 0; x < w; x++){
for(int r = 0; r < kMaxCircleR; r++){
int cnt = counter.get((y * w + x) * kMaxCircleR + r);
if(max_count < cnt){
max_count = cnt;
x_max = x;
y_max = y;
r_max = r;
}
}
}
}
if(max_count < kMinCount) break;
Tuple3 t3 = new Tuple3<Integer, Integer, Integer>(x_max, y_max, r_max);
result.add(t3);
System.out.println(" カウント:" + max_count + " 中心:(" + x_max + "," + y_max + ") 半径:" + r_max);
// 類似した周辺のカウントを消去する
for(int y = -5; y <= 5; y++){
int y2 = y_max + y;
if(y2 < 0 || y2 >= h) continue;
for(int x = -5; x <= 5; x++){
int x2 = x_max + x;
if(x2 < 0 || x2 >= w) continue;
for(int r = -5; r <= 5; r++){
int r2 = r_max + r;
if(r2 < 0) continue;
counter.set((y2 * w + x2) * kMaxCircleR + r2, 0);
}
}
}
}
return result;
}
// 円を書き出す
private static void drawHoughCircle(BufferedImage image, ArrayList<Tuple3> list){
Graphics2D g2d = (Graphics2D)image.getGraphics();
g2d.setColor(Color.RED);
for(Tuple3<Integer, Integer, Integer> temp : list){
int x = temp.t1, y = temp.t2, r = temp.t3;
g2d.drawOval(x - r, y - r, r * 2, r * 2);
}
}
}
// タプル
class Tuple2<T1, T2>{
public T1 t1;
public T2 t2;
public Tuple2(){}
public Tuple2(T1 t1, T2 t2){
this.t1 = t1;
this.t2 = t2;
}
}
class Tuple3<T1, T2, T3>{
public T1 t1;
public T2 t2;
public T3 t3;
public Tuple3(){}
public Tuple3(T1 t1, T2 t2, T3 t3){
this.t1 = t1;
this.t2 = t2;
this.t3 = t3;
}
}