目次
- 第1章では、線形計画問題や整数計画問題についての簡単な説明を行います
- 第2章では、線形計画問題の代表的な解法であるシンプレックス法についての解説を行います
- 第3章では、整数計画問題の代表的な解法である分枝限定法についての解説を行います
- 第4章では、それらの記述のまとめと、おまけテキストについて記述します
なお、今回制作したMIPソルバーは、次のURLに置いてあります。
SMIPS(The Smallest MIP Solver)
第1章 概要
何かを最適化したい、と思ったことはありませんか?
『最短ルートを探したい』『物をうまく詰め込みたい』『誰もが納得するスケジュールを組みたい』……。昔は人間が試行錯誤して決めていた問題も、今ではコンピューター任せで解くことができます。ですがその裏には、多くの科学者や技術者の血と汗と涙がありました。
この記事では、最適化問題の一種である、整数計画問題を解くためのソルバーを作ります。
分かりやすく書いたつもりですが、とても小じんまりした実装なので性能は察してください。
※説明の都合上、かなりの長文となります。
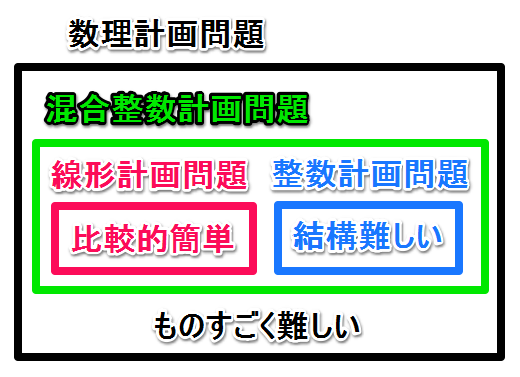
整数計画問題とは?
まずは数理計画問題から説明しましょう。これは、制約式を設定した上で、目的関数を最大化 or 最小化させる問題全てを指します。
これには、『$X^2+Y^2\leq1$ かつ $Y\geq X^3$の範囲内で、$XY$の最大値を求めよ』のような複雑な問題も含まれます。
それを少し簡単にして、目的関数や制約式が一次式で表される数理計画問題を混合整数計画問題と呼びます。
つまり、『$3X+Y\leq10$かつ$X+2Y\leq7$の範囲内で、$5X+4Y$の最大値を求めよ(ただしYは整数)』のような問題です。
ここで名前に『混合』と付いているのは、『各変数が整数の範囲か、それとも実数の範囲か』といった条件を考慮する必要があるからです。理由は後述しますが、一般に整数変数が多いほど難しい問題になります。
なお、全ての変数が整数であるものを整数計画問題、全ての変数が実数であるものを線形計画問題と呼びます。
……以上の問題の関係性について、図にしてみるとこんな感じです。
線形計画問題の解き方について
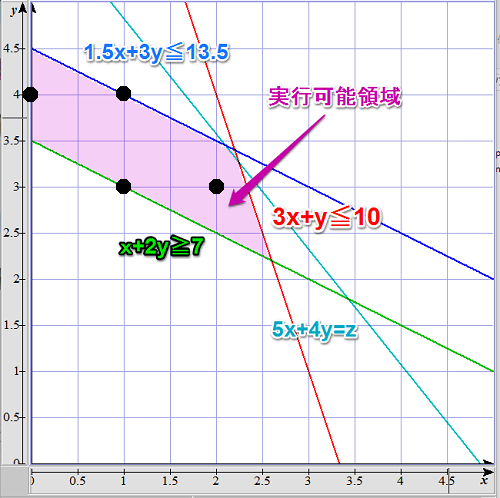
まずはサンプル問題をご覧ください(以下、XとYは0以上の数であるものとします)。
グラフにおける3つの不等式『$3x+y\leq10$』『$1.5x+3y\leq13.5$』『$x+2y\geq7$』に囲まれた紫の領域が、制約式を満たす範囲である実行可能領域です。この範囲の中で、目的関数『$5x+4y$』が最大になる$(x, y)$の値を求めることを考えます。
整数計画問題だと、実行可能領域の中で変数が整数値を取るもの限定で探すことになりますが、まずは整数条件を無視した場合……つまり緩和問題の解き方について考えてみましょう。
注目したいポイントは、制約式が一次式なので、実行可能領域は凸包体であるということです。三次元の物体で例えると、『皮を剥いた後のジャガイモ』がイメージとして一番近いでしょうか。
説明は省略しますが、凸包体であることにより、その頂点の何処かに求めたい解があることが保証されます。頂点の座標は連立方程式を解けば簡単に出せますので、愚直に考えますと、全ての頂点を調べれば必ず最適な解が出せます。
……ただ、制約式をM本、変数をN個とすると頂点は$\frac{(M+N)!}{M!N!}$個もありますので、虱潰ししていると計算時間が掛かりすぎてしまいます。そこで、『どこか適当な頂点(実行可能解)からスタートして、辺伝いに進むことで最適な頂点を見つける』といった手法が開発されました。ジョージ・ダンツィク氏が1947年に発見したその手法のことを**シンプレックス法(単体法)**と呼びます。その手順については後述しますが、計算がとても高速で、しかも実装が簡単なのが特徴です。
※実は『内点法』と総称される特殊な手段を用いれば、最悪のケースでも計算時間が多項式時間で抑えられることが分かっていますが、今回はその説明を省略します。
整数計画問題の解き方について
先ほどの図の黒い点に注目してください。あの点は、実行可能領域内における格子点……つまり『変数の値が全て整数となる点』を表してます。
緩和問題の解(緩和解)がそのまま格子点なら理想ですが、実際はそう上手くいくとは限りません。
そこで、緩和問題に処理を施すことによって、『どうすれば緩和解が格子点の上に乗るのか』を考えることにしました。
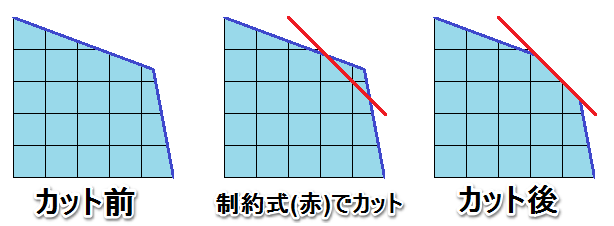
最初に考え出されたのは、緩和解が整数条件を満たさなければ、その緩和解だけを上手く削るように新たな制約式を追加するといった作戦でした(切除平面法)。上手く削っていくと、最終的には緩和解が整数条件を満たすようになります。
……ただ、切除平面法だけでは、実用上使い物にならない(結果が出るまでの速度が遅すぎる)といった問題がありました。
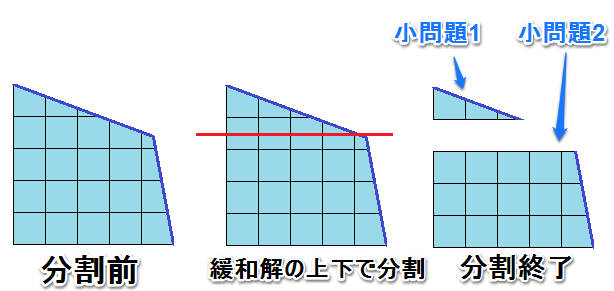
そこで、今度は問題を分割し、小問題の解を探索するといった作戦が考え出されました(分枝限定法)。
分枝限定法では、緩和解が整数条件を満たさない場合、満たさない変数を1つ選んで問題を分割します。
例えば、「$X=2,Y=3.5$」といった結果が出た場合、次の2つの小問題に分割した上で計算を行います。
最終的には両方計算して、より良い結果が出た方の解を採用するということですね。
- 元の問題に「$Y\leq3$」を付け足した問題
- 元の問題に「$Y\geq4$」を付け足した問題
見ための問題数が増えるため、時間の無駄に見えますがさにあらず。分割を上手く利用すれば、緩和問題を解いた段階で無駄な探索を省ける場合があるのです。
例えばある小問題の緩和解を求めた際、結果が『解なし』となったとします。『緩和問題の解は元の問題の解より悪くならない』といった性質がありますので、その小問題については分枝するまでもなく駄目だと判明します。
また、ある小問題でとりあえず整数解(許容解)が出ていたとします。『許容解は元の問題の解より悪くならない』といった性質がありますので、許容解よりも悪い緩和解を出した小問題については分枝するまでもなく駄目だと判明します。
こうして無駄な小問題を切っていくと、計算量が大幅に節約できます。先に説明した切除平面法よりも分かりやすく速くなるので、数理計画法について学ぶ際は是非マスターしておきたいところです。
第2章 シンプレックス法の実装
MIPソルバーへの足がかりとして、まずは線形計画問題(Linear Problem)を解けるようになりましょう。
そのための一番手っ取り早い方法としては、いかに説明するシンプレックス法があります。
ただ、ググって出てくるテキストが間違っていることが珍しくありませんので、学ぶのに結構苦労しました……。
データ構造
実装しやすければ何でも構わないのですが、例えば次のような実装となります。
// 比較演算子(順に「≦」「=」「≧」を表す)
enum class Compare {
Less,
Equal,
Greater,
};
class MIP {
size_t v_cnt; //! 変数の数
size_t e_cnt; //! 制約式の数
vector<double> obj; //! 目的関数の係数 obj[v_cnt]
vector<vector<double>> e_left; //! 制約式の左辺係数 e_left[e_cnt][v_cnt]
vector<Compare> e_compare; //! 制約式の比較演算子 e_compare[e_cnt]
vector<double> e_right; //! 制約式の右辺係数 e_right[e_cnt]
deque<bool> integer_flg; //! 整数変数ならtrue integer_flg[v_cnt]
};
C++はクラスベースのオブジェクト指向言語ですので、問題をクラスとして定義するのが妥当でしょう。
もちろん、制約式部分は「vector<Equation> constraint;」などとして、別途クラスにしてしまう手もあります。
上記のクラスで、第1章のサンプル問題を数値化すると次のように書けます。
MIP query = {
2, 3, {5, 4}, {
{1.5, 3},
{3, 1},
{1, 2}
},
{Compare::Less, Compare::Less, Compare::Greater},
{13.5, 10, 7}, {true, true}
};
シンプレックス法
いよいよシンプレックス法に移りますが、その手順は大きく分けて3ステップ。
- 問題から単体表を作成する
- 単体表から列(変数)・行(制約式)をピポッド選択して、そこを基準に掃き出す
- 終了条件を満たせば終了。そうでない場合は、ピポッド選択と掃き出しを繰り返す
この『選択と掃き出し』が結構曲者で、順番を間違えると永遠に最適解に辿り着けないことがあります。
とはいえ、正しい順番で掃き出しすれば『いつか必ず最適解に辿り着く』ことも保証されてます。
以下、シンプレックス法の解説のため、第1章のサンプル問題から3番目の制約式を省いた形で解いてみます。
単体表の作成
解きたい問題は次のように表されます。
- 最大化する目的関数:$5X+4Y$
- 制約式1:$1.5X+3Y\leq13.5$
- 制約式2:$3X+Y\leq10$
- 変数の範囲:$X\geq0$, $Y\geq0$
まず、制約式の不等号が「≦」となっているものについて、別途変数を追加します。
この、『等号に持っていくためにワザと追加する変数』のことをスラック変数と呼びます。
- 最大化する目的関数:$Z=5X+4Y$
- 制約式1:$1.5X+3Y+s1=13.5$
- 制約式2:$3X+Y+s2=10$
- 変数の範囲:$X\geq0$, $Y\geq0$, $s1\geq0$, $s2\geq0$
次に、そうしたスラック変数を加えた問題から単体表を初期化します。
ただしここでは、説明しやすいようにX・Y・s1・s2をP1・P2・P3・P4と表記してます。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 |
|---|---|---|---|---|---|
| P3 | 13.5 | 1.5 | 3 | 1 | 0 |
| P4 | 10 | 3 | 1 | 0 | 1 |
| z | 0 | -5 | -4 | 0 | 0 |
見ての通り、基底変数がzの行以外は、そのまま係数を入力すればOKです。
また、zの行では、最大化する目的関数の係数を-1倍して入力します。
なお、ここでは『スラック変数の数が制約式の数と同じである』ことを暗黙の了解としています。
基底変数の欄に、何の説明もなくスラック変数の名前が順番に書いてあるのはそのためです。
『不等号が≧だったり=だったりしたらどうするのか』というのは当然の疑問ですが、その場合は後述します。
ピポッド選択
ここで単体表のzの行を見てみましょう。(最初の段階だと当然ですが)P1以降の列には、値がマイナスな列がありますね?
列選択の際は、『zの行で、値がマイナスな列(複数ある場合はなるべく変数の添字が小さいもの)』を選択します。
ここで選択できる列が存在しない=シンプレックス法の反復処理終了の合図です。
この問題の場合、zの行の中で値が-5であるP1の列が選択されます。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 |
|---|---|---|---|---|---|
| P3 | 13.5 | 1.5 | 3 | 1 | 0 |
| P4 | 10 | 3 | 1 | 0 | 1 |
| z | 0 | -5 | -4 | 0 | 0 |
| 【選択1】 | ― | ☆ |
また、今度は選択した列を縦に見ていきます。各行について、『右辺係数÷選択した列の値』の値を見ていき、その値が最小の行を選択します。
ただし、選択した列の値が0なら無条件で飛ばします。また、『右辺係数÷選択した列の値』の値が同じなら、基底変数の添字が小さいものを優先させます。ここで選択できなかった場合は反復終了……というよりは解なしの合図です。
この問題の場合、『右辺係数÷選択した列の値』の値が3.33...であるP4の行が選択されます。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 | 右辺÷選択列 | 【選択2】 |
|---|---|---|---|---|---|---|---|
| P3 | 13.5 | 1.5 | 3 | 1 | 0 | 9 | |
| P4 | 10 | 3 | 1 | 0 | 1 | 3.33 | ☆ |
| z | 0 | -5 | -4 | 0 | 0 | ― | ― |
| 【選択1】 | ― | ☆ | ― | ― |
掃き出し
ここの処理は、ガウスの消去法などを知っている方にとっては馴染み深いものではないかと思われます。
つまり、【選択2】で選択した行を、【選択1】の列の係数で割り算した後、他の行に対して積和すればOKです。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 |
|---|---|---|---|---|---|
| P3 | 8.5 | 0 | 2.5 | 1 | -0.5 |
| P1 | 3.33 | 1 | 0.33 | 0 | 0.33 |
| z | 16.67 | 0 | -2.33 | 0 | 1.67 |
ここで、【選択2】で選択した行について、基底変数の表記が変わっていることに気づかれたかと思います。
シンプレックス法の場合は、掃き出し処理を行った後、基底変数の添字が【選択1】で選択した列の変数に変更されます。
反復処理
後は、ピポッド選択の項でも書きましたように、zの行から負の数が消えるまで反復計算します。
ちなみに、前述のようなピポッド選択の基準をBland の最小添え字規則と呼びます。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 | 右辺÷選択列 | 【選択2】 |
|---|---|---|---|---|---|---|---|
| P3 | 8.5 | 0 | 2.5 | 1 | -0.5 | 3.4 | ☆ |
| P1 | 3.33 | 1 | 0.33 | 0 | 0.33 | 10 | |
| z | 16.67 | 0 | -2.33 | 0 | 1.67 | ― | ― |
| 【選択1】 | ― | ☆ | ― | ― |
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 |
|---|---|---|---|---|---|
| P2 | 3.4 | 0 | 1 | 0.4 | -0.2 |
| P1 | 2.2 | 1 | 0 | -0.13 | 0.4 |
| z | 24.6 | 0 | 0 | 0.93 | 1.2 |
そして、反復計算が終了した際、『右辺係数』の列に最適解が現れます。
zの行にその際の目的関数の値、他の行にその際の各変数の値が現れます(出てこない変数の値は0)。
この場合は、P1(つまりX)が2.2、P2(つまりY)が3.4ならば、目的関数5X+4Yの最適値が24.6になるということです。
2段階法
○シンプレックス法の問題点
さて、シンプレックス法の解説の際、第1章のサンプル問題から3番目の制約式を抜きました。
これは、不等号が≦以外の場合についての処理方法を記述する必要があるからです。
より正確に言えば、『右辺が負なら正になるように正規化し、その上で不等号が≦でない場合の処理』ということになります。
実は、シンプレックス法はその性質上、何らかの実行可能解(頂点)伝いにしか探索できません。
つまり、何でもいいので実行可能解を用意する必要があるのです。
先の条件(右辺が負でない&不等号が≦)の際は、とりあえずスラック変数=右辺の値にするだけで実行可能解になります。
- $1.5X+3Y\leq13.5\Rightarrow1.5X+3Y+s1=13.5\Rightarrow X=Y=0,s1=13.5$は実行可能解の1つ
- $3X+Y\leq10\Rightarrow3X+Y+s2=10\Rightarrow X=Y=0,s2=10$は実行可能解の1つ
一方、≧が含まれている場合、単に符号を反転させると、『(スラック変数含めて)変数が負の値を取らない』仮定と矛盾します。
- $X+2Y\geq7\Rightarrow -X-2Y\leq-7\Rightarrow -X-2Y+s3=-7\Rightarrow X=Y=0,s3=-7$は実行可能解の1つにならない!
また、=が含まれる式の場合にも対処する必要があります(≧と≦を同時に指定する方法でもいいが、前述の理由により矛盾が生じる)。
つまり、単にシンプレックス法だけ実装したのでは片手落ちということです。
○人為変数の登場
そこで導入されるのが人為変数と呼ばれるものです。どこに投入されるかは次のソースコードをご覧ください。
size_t a_cnt = 0; // 人為変数の数
for (size_t i = 0; i < e_cnt; ++i) { // 制約式の数だけループ
//! 各制約式を見て判断する
if (e_compare[i] == Compare::Equal) {
//! 等号なら人為変数+1
++a_cnt;
}
else {
//! 不等号ならスラック変数+1
++s_cnt;
/**
* 基底可能解を求めるために、人為変数が必要な場合に+1
* つまり、『右辺が負で不等号が≦』『右辺が正で不等号が≧』
* の場合に+1される
*/
if(e_right[i] < 0.0 && e_compare[i] == Compare::Less
|| e_right[i] >= 0.0 && e_compare[i] == Compare::Greater) {
++a_cnt;
}
}
}
つまり、制約式は次の3つに場合分けされます。
| 右辺を正にした際の不等号 | スラック変数 | 人為変数 | 備考 |
|---|---|---|---|
| ≦ | ○ | × | スラック変数の係数が+1 |
| = | × | ○ | スラック変数の係数が0 |
| ≧ | ○ | ○ | スラック変数の係数が-1 |
また、これにより、サンプル問題は次のように変形されます。s1~s3がスラック変数、a1が人為変数です。
- 最大化する目的関数:$Z=5X+4Y$
- 制約式1:$1.5X+3Y+s1=13.5$
- 制約式2:$3X+Y+s2=10$
- 制約式3:$X+2Y-s3+a1=7$
- 変数の範囲:$X\geq0$, $Y\geq0$, $s1\geq0$, $s2\geq0$, $s3\geq0$, $a1\geq0$
- 以下の単体表では、XとYはP1とP2、s1~s3はP3~P5、a1はP6とする
○1段階目の目標:実行可能解を見つける
1段階目で重要なのは、とにかく元の問題における実行可能解を見つけるということです。
そのため、目的関数を『人為変数の和が最小化する』ように変更します。
- 最大化する目的関数:$Z=-a1$
これにより、最適化が終了すると、人為変数が全て0になっているはずです(ならない場合は解なし)。
ただ、これをそのまま実行しようと単体表を記述しても、zの行に負数が無いので最適化されないといった問題があります。
(人為変数がある行の添字は、人為変数の添字となることに注意。詳しくはソースコードを読むべし)
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|---|
| P3 | 13.5 | 1.5 | 3 | 1 | 0 | 0 | 0 |
| P4 | 10 | 3 | 1 | 0 | 1 | 0 | 0 |
| P6 | 7 | 1 | 2 | 0 | 0 | -1 | 1 |
| z | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
そこで、zの行は最初にオール0で初期化した後、人為変数を含むすべての行で引き算します。
今回は人為変数を含む制約式が1つしかないため、P6の行の数値を反転させただけに見えますが……。
(細かい話ですが、引き算する列は通常変数・スラック変数の列のみです)
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|---|
| P3 | 13.5 | 1.5 | 3 | 1 | 0 | 0 | 0 |
| P4 | 10 | 3 | 1 | 0 | 1 | 0 | 0 |
| P6 | 7 | 1 | 2 | 0 | 0 | -1 | 1 |
| z | -7 | -1 | -2 | 0 | 0 | 1 | 0 |
後は普通に単体表の処理を行います。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|---|
| P3 | 3 | 0 | 0 | 1 | 0 | 1.5 | -1.5 |
| P1 | 2.6 | 1 | 0 | 0 | 0.4 | 0.2 | -0.2 |
| P2 | 2.2 | 0 | 1 | 0 | -0.2 | -0.6 | 0.6 |
| z | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
○2段階目の目標:通常の最適化処理を行う
こうして実行可能解が1つ見つかりました。後は、普通にシンプレックス法をもう一度実行すれば最適解が求まります。
ただし、どのようにzの値を書き換えるかが最大のネックとなります。
事前に調べた際は、複数の大学のWebページの記述が誤っているという悲惨な状況でした。
(詳細はGitHubのSMIPSのページにあるReadme.mdを参照してください)
そこで、正しく動いた、参考文献にある『PHPSimplex』のサイトの手法をそのまま採用します。
//! 単体表のzの行における、人為変数以外の列を0クリアする
for (size_t j = 0; j <= v_cnt + s_cnt; ++j) {
sm.table[e_cnt][j] = 0.0;
}
//! 単体表のzの行から、本来の目的関数の係数を引く
for (size_t j = 1; j <= v_cnt; ++j) {
sm.table[e_cnt][j] = -obj[j - 1];
}
//! 単体表のzの行から、単体表の他の行×係数を引く
//! 係数は、単体表の他の行における添え字によって変化する
for (size_t j = 0; j <= v_cnt + s_cnt; ++j) {
for (size_t i = 0; i < e_cnt; ++i) {
if (sm.v_idx[i] < v_cnt) {
//! 本来の変数の範囲内だと、係数=目的関数の係数
sm.table[e_cnt][j] += obj[sm.v_idx[i]] * sm.table[i][j];
}
else if (sm.v_idx[i] < v_cnt + s_cnt) {
//! スラック変数の範囲内だと、係数=0
}
else {
//! 人為変数の範囲内だと、係数=-1
sm.table[e_cnt][j] += (-1.0) * sm.table[i][j];
}
}
}
これにより、2段階目の計算開始時の単体表は次のようになります。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 | P5 |
|---|---|---|---|---|---|---|
| P3 | 3 | 0 | 0 | 1 | 0 | 1.5 |
| P1 | 2.6 | 1 | 0 | 0 | 0.4 | 0.2 |
| P2 | 2.2 | 0 | 1 | 0 | -0.2 | -0.6 |
| z | 21.8 | 0 | 0 | 0 | 1.2 | -1.4 |
ここから改めてシンプレックス法を施せば、求める最適解が導き出せます。
| 基底変数 | 右辺係数 | P1 | P2 | P3 | P4 | P5 |
|---|---|---|---|---|---|---|
| P5 | 2 | 0 | 0 | 0.67 | 0 | 1 |
| P1 | 2.2 | 1 | 0 | -0.13 | 0.4 | 0 |
| P2 | 3.4 | 0 | 1 | 0.4 | -0.2 | 0 |
| z | 24.6 | 0 | 0 | 0.93 | 1.2 | 0 |
第3章 分枝限定法の実装
分枝限定法を擬似言語で書き下すと次の通りです。
AnswerMIP branch_bound(const AnswerMIP provisional){
//! 緩和問題の解を求める
AnswerLP answer_lp = this->simplex_method();
//! 緩和解が実行不可能解 or 非有界なら弾く(限定操作)
if(answer_lp == INFEASIBLE){
return provisional;
}
//! 緩和解が暫定解より悪ければ弾く(限定操作)
if(answer_lp <= provisional){
return provisional;
}
//! 整数条件を満たしていれば、暫定解として出力する
if(isIntegerCondition(answer_lp)){
return (AnswerMIP)answer_lp;
}
/**
* 分枝操作
* 「右」の枝で計算した後に、「左」の枝で計算する
* 「右」の枝で計算した暫定解が「左」の枝に使われるのがポイント
*/
MIP branch_right = this->make_branch(RIGHT);
AnswerMIP answer_right = branch_right.branch_bound(provisional);
MIP branch_left = this->make_branch(LEFT);
return branch_left.branch_bound(answer_right);
}
MIP problem("problem.txt");
AnswerMIP answer = problem.branch(INFEASIBLE);
これだけだとシンプルに見えますが、『どの変数から分割するか』はソルバーにとって重大なノウハウです。
なぜなら、どの変数から分枝するかによって、効率よく小問題を振り落とせるか……つまり速くなるかが決まるからです。
冒頭で紹介した自作ソルバー(SMIPS)では単に「添字が小さい方」から分枝させていますが、単に実装が面倒だったからですね。
第4章 まとめ
以上の手順を踏めば、誰でもMIP(混合整数計画問題)ソルバーを作ることが可能だと思われます。
より高速にしたい場合は、GLPKやSCIPなど、既存のソフトウェアのソースコードを読んでみると良いでしょう。
参考文献も参照くださいませ。
よくある質問
○問題中の変数がマイナスの値を取れるようにしたい
元の変数を$X$とします。すると、これは2つの変数を用いて$(W_1-W_2)$と置き換えられます。
ここで$W_1\geq0$かつ$W_2\geq0$とすれば、$X$はマイナスの値を取れますので、問題なく計算できます。
○問題文中の変数に範囲指定を付けたい
仮に$A\leq X\leq B$とします。タダの範囲指定なら制約式内に『$X\geq A$』『$X\leq B$』などと掛けばOKです。
Xが負の値もとり得る場合は、前述のように$(W_1-W_2)$と置き換えます。
つまり、『$-3\leq X\leq 5$』とあれば、『$(W_1-W_2)\geq-3$』『$(W_1-W_2)\leq5$』と書くことになります。
○最小化問題を解きたい・目的関数無しで解きたい
前者の場合、目的関数の係数の符号を逆にすればOKです。
後者の場合、係数はデタラメでもいいので適当な目的関数をでっち上げてください。
これはプログラム上の都合というよりも、目的関数が無いと探索が遅くなるというソルバ共通の悩みのためです。