【E資格対策04】02_機械学習

はじめに

今回記事作成者のE資格受験勉強のために記事を作成しています
間違いなどありましたらコメントにてご指摘いただけると幸いです。

目的

E資格のシラバスの内容の用語について理解を深める。

E資格のシラバスの内容

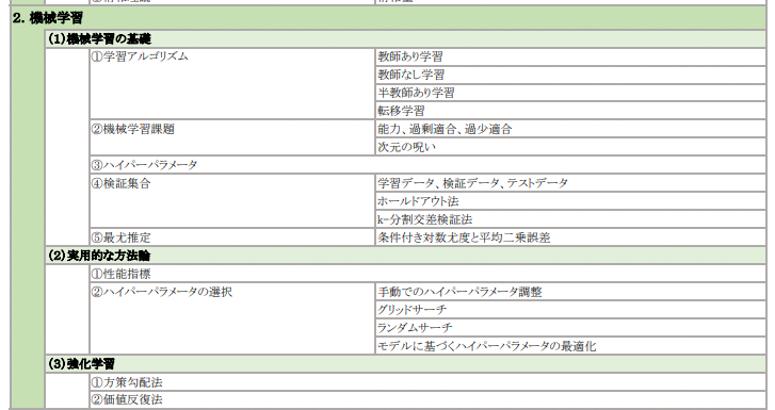
2. 機械学習

(1) 機械学習の基礎

①　学習アルゴリズム

教師あり学習

教師あり学習では、人間があらかじめ付けた正解のラベルに基づき、機械が学習を行い、データセットに対する応答値の予測を行うモデルを構築します。

教師なし学習

教師なし学習では、入力データのみがあり、ペアとなる正解のデータは存在しません。
ゴールは、データに対する理解を深めるためにデータの基本的な構造や分布をモデル化することです。

参考URL：

半教師あり学習

半教師あり学習は、入力データが多く、一部のみ人間などの手でラベル付けされているものを言います。
これは教師あり学習と教師なし学習の間に位置します。

転移学習

・転移学習とは、効果的な仮説を効率的に見つけ出すために、別のタスクで学習された知識を転移する機械学習の手法である。
・転移学習に学習済みモデルを転用することで、大量のデータと学習にかかる時間を削減することができる。

参考URL：

②　機械学習課題

能力

過剰適合

過小適合

過剰適合や過適合や過学習とは、統計学や機械学習において、訓練データに対して学習されているが、未知データに対しては適合できていない、汎化できていない状態を指す。汎化能力の不足に起因する。
その原因の一つとして、統計モデルへの適合の媒介変数が多すぎる等、訓練データの個数に比べて、モデルが複雑で自由度が高すぎることがある。不合理で誤ったモデルは、入手可能なデータに比較して複雑すぎる場合、完全に適合することがある。
対義語は過少適合や過小学習。

参考URL：

次元の呪い

次元の呪いとは、機械学習に用いるデータの属性数（＝次元）が大きくなった時に発生する問題
それは大きく2つの問題に大別することが可能で、その2つとはData sparsity（データの希薄性）とDistance concentration（距離集中）です。

参考URL:

③　ハイパーパラメーター

ハイパーパラメータでのベイズ探索
ベイズ探索で使われるベイス最適化とは、ガウス家庭によって予測した平均、分散から獲得関数を最適化して探索点を取得し、評価しながらガウス家庭を更新するアルゴリズムである。
ベイズ探索では、探索されていない範囲と既知の最大値（最小値）に近い範囲をうまく選択しながら探索するため、グリッドサーチに比べ、計算時間が短い
ベイズ最適化では、平均が大きくなると局所解になる恐れがあり、分散が大きいと周りが探索されていないため、どういった値になるかわからない点も調べなくてはいけない。

④ 検証集合

学習データ

モデルが賢くなるために使うデータ
モデルを学習するために使うデータ

検証データ

ハイパーパラメータを調整するために使うデータ

テストデータ

学習済モデルの汎用性を評価するために使うデータ

k-分割交差検証法

K分割交差検証法は、元のデータをk個にランダムに分割します。k個のデータはそれぞれ順番に検証セットとして使われ、残りのデータセットは学習セットとしてモデルをあてはめるのに使用されます。合計で、k個のモデルがあてはめられ、k個の検証結果が得られます。検証セットから計算された統計量が最良のものが、最終的なモデルとして選ばれます。この方法は、少ないデータを効率的に利用するので、小規模なデータセットに適しています。

参考URL：

ホールドアウト法

ホールドアウト法（hold-out）とは、データを学習データと検証用のデータに分割してモデル評価を行う方法です。
ホールドアウト法は、モデルを作る学習データ（x_train,y_train）と、モデルを評価するテストデータ（x_test,y_test）に分割して評価します。
学習したモデルで予測する際に、学習に使っていない未知のデータで予測します。
よってデータを分けることで、汎化性能（未知のデータに対する性能）を向上させることができます。
ホールドアウト法は大量のデータセットがあり、モデルの推論に時間がかかる場合などに利用されます。

参考URL:

⑤　最尤推定

条件付き対数尤度（尤度：ゆうど）

対数尤度関数尤度関数の対数をとる
(条件つき確率の）対数尤度関数という。
○ log は単調増大関数だから対数尤度関数を
最大にするパラメータが最尤推定量
○ H(w) = -(1/n) log L(w) と書けば L(w)= exp(-nH(w))
○ 尤度関数と対数尤度関数はどちらを考えても同じだが
計算上対数尤度関数のほうが便利なことが多い。

参考URL：条件付き対数尤度と平均二乗誤差

平均二乗誤差

誤差の 2 乗を全て足し合わせた量を、平均二乗誤差
(MSE: mean squared error) と呼びます。最小二乗法は、この平均二乗誤差が最も小さくなる
ようにパラメータ θ0、θ1 の値を決定する方法です。

参考URL：条件付き対数尤度と平均二乗誤差

(2) 実用的な方法論

① 性能指標

機械学習のモデルを作成した際に、そのモデルがどれくらい「良い」モデルなのかを判断するためには、評価指標を確認する

参考URL：

② ハイパーパラメータの選択

手動でのハイパーパラメーター調整

ハイパーパラメータ（英語：Hyperparameter）とは機械学習アルゴリズムの挙動を設定するパラメータをさします。少し乱暴な言い方をすると機械学習のアルゴリズムの「設定」です。

参考URL：

グリッドサーチ

グリッドサーチとは与えられたハイパーパラメータの候補の値の全パターンのモデル構築を行う手法です。
グリッドサーチは調整するハイパーパラメータの数が少ない場合やある程度の「あたり」がついている場合に使用することが多い手法です。全組み合わせのモデル訓練を行うので、大規模データなど訓練時間が長い場合はグリッドサーチを使うことは滅多にありません。

【メリット】
調整する値の「あたり」が付いている場合は◎
調整する値の数が少ない場合は◎

【デメリット】
モデル訓練回数が増えるので時間が掛かる
計算コストが非常に高い

ランダムサーチ

前項のグリッドサーチは候補の値の全パターンのモデル訓練を行いました。対してランダムサーチは候補の値をランダムに組み合わせたモデル訓練を行いハイパーパラメータを検証する手法です。
ランダムサーチの場合は検証するためのモデル訓練の回数を指定します。

【メリット】
調整する値が多くても対応することが可能

【デメリット】
ランダムに検証するので「運任せ」の要素あり

モデルに基づくハイパーパラメータの最適化

(3) 強化学習

① 方策勾配法

方策ベースは、価値を最大化する方策を得るために、方策勾配法を利用し、方策を改善する方法のカテゴリです。
REINFORCEやVanillaは、方策ベースに分類されます。

方策ベース：明示的な方策があり、現在の方策を改善するアルゴリズム。価値関数は内部的に有するが、行動選択に影響を与えない。まず「方策」を決めてからその「方策」の「価値」を高めるように「方策」を改善していく。
価値ベース：明示的な方策はなく、サンプルから学習し、最適な価値関数の値を逐次推定するアルゴリズム。「価値」を求めたうえでその「価値」を高めるような「方策」を選択する。（厳密には方策自身はあるが、価値関数が最大の方策を常に選択する）

方策反復法
方策をモデル化して直接最適化する
AlphaGOのアプローチ

参考URL：

② 価値反復法

方策を価値で記述して価値の推定を頑張る。
DQNのアプローチ

DQNとは、Deep Q-Networkの略です。
Q学習ではQ値を学習し、Qテーブルを完成させることに重きが置かれていましたが、DQNではQ学習にニューラルネットワークの考え方を含めています。
最適行動価値関数をニューラルネットを使った近似関数で求め、ある状態”_”のときに行動ごとのQ値を推定できれば、一番いいQ値の行動=取るべき最善の行動がわかるという仕組みです。
ある状態”sₜ”を入力し、行動”a”が出力層のノードとなるようなニューラルネットワークを使用して”Q(sₜ, aₜ)”の値を計算します。

Q学習とは、ある状態のときにとったある行動の価値を、Qテーブルと呼ばれるテーブルで管理し、行動する毎にQ値を更新していく手法です。

参考URL：

参考書籍

徹底攻略ディープラーニングE資格エンジニア問題集 第2版 [ スキルアップAI株式会社　小縣 信也 ]