JPL Solar System Dynamics(SSD)が供給しているAPIの使い方を記しておきます。今回は3体問題の軌道の初期解(JPL Three-Body Periodic Orbit Catalog)のデータベース(i.e., $[x_0,y_0,z_0,v_{x0}, v_{y0}, v_{z0}, C, \tau, \lambda]$, $C$: Javobi constant, $\tau$: period, $\lambda$: stability)をJSONファイルに持っていくことがゴールです。
- System (e.g., Sun-Earth)
- Orbit Family (e.g., Halo, North)
- Liberation Point
- Jacobi Constant (range)
- Period (range)
- Stability index (range)
を入力すれば対応する軌道のデータベースを返してくれる便利なGUIもあるのですが、毎回手動でデータを回収するのは少し面倒なので...
Pythonでの呼び出し方
例として、Earth-Moon, L1 Halo 軌道(North)のデータを取っていきます。
import requests
import json
r = requests.get("https://ssd-api.jpl.nasa.gov/periodic_orbits.api?sys=earth-moon&family=halo&libr=1&branch=N")
r = r.json()
# write the json file
with open('filename.json', 'w') as f:
json.dump(r, f)
(参考) Juliaでの呼び出し方
using HTTP
using JSON
r = HTTP.get("https://ssd-api.jpl.nasa.gov/periodic_orbits.api?sys=earth-moon&family=halo&libr=1&branch=N")
s = String(r.body)
# save the json file
open("filename.json", "w") do f
write(f, json_string)
end
これで得た初期値を、試しに手元にあるPythonのCR3BP (synodic frame) propagatorで積分してみます。
# load json file
f = open('data.json',)
data = json.load(f)
tof = 3.1 # TU, 今回は適当に値を決めました。
df = pd.DataFrame(data["data"])
# find the closest initial solution. df.iloc[:,7] is a column for period.
row = df.loc[(df.iloc[:,7]-tof).abs().argsort()[0]]
s0 = row[0:6]
mu = float(data["system"]["mass_ratio"])
pos, _ = propagate_cr3bp(s0, mu, tof) # 手元にあるCR3BPのintegrator
# Plot the orbits
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot(pos[:,0], pos[:,1], pos[:,2])
# find the fixed points
l1, _, _, _, _ = find_lagrangian_pts(mu) # ラグランジュ点を見つけてくれる関数
ax.scatter(l1[0], l1[1], l1[2], marker='D', s=25.0, facecolors="none", color='black', label='L1')
ax.scatter(1-mu, 0.0, 0.0, marker='*', s=25.0, color='orange', label='L1')
plt.show()
結果
(Differential Correction無しでも)良い感じにHalo軌道が出てきました。
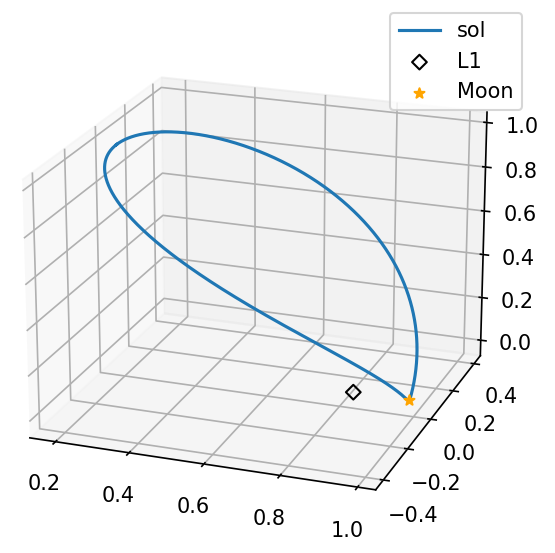
因みに、初期値が
[1.879665e-01, 0.000000e+00, 9.752153e-01, -2.824989e-12, 8.038017e-01, 2.179037e-12]
なので、データベースの値はapoapsisの値(画像左上端)であることが分かります。