この記事はレイトレ Advent Calendar 2017の記事として執筆しました。
遅刻しちゃってすみません。。。ゼノブレイド2が面白すぎたのです。。。
円錐台
ちょっとお仕事のほうで珍しくレイと円錐台との衝突判定が必要になりまして、
わざわざピンポイントでこの図形をレンダリングしようとする人も少ないと思いますし、せっかくなので、備忘録的にまとめておこうと思います。
今回レンダリングするのは以下の形状です。
円錐の方程式
Web上で良さそうなのを色々調べた結果、結局PBRT v3に普通に使い勝手の良いものが載っており、だいぶ時間を浪費してしまいました。いくつか違う表現も見つかりましたが、今回はPBRTのものを紹介します。
{ \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ \left( y-h \right) }^{ 2 }=0
イメージを掴むためにいくつか特殊なケースを考えてみます。
$ y = 0 $ の場合、
{ \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ \left( y-h \right) }^{ 2 }=0\\ { \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ \left( 0-h \right) }^{ 2 }=0\\ { \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ h }^{ 2 }=0\\ { \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ h }^{ 2 }=0\\ \frac { { h }^{ 2 } }{ { r }^{ 2 } } { x }^{ 2 }+\frac { { h }^{ 2 } }{ { r }^{ 2 } } { z }^{ 2 }-{ h }^{ 2 }=0\\ \frac { 1 }{ { r }^{ 2 } } { x }^{ 2 }+\frac { 1 }{ { r }^{ 2 } } { z }^{ 2 }-1=0\\ { x }^{ 2 }+{ z }^{ 2 }-{ r }^{ 2 }=0\\ { x }^{ 2 }+{ z }^{ 2 }={ r }^{ 2 }
おお、x, z の座標系で半径 $ r $ の円の方程式になりました。
しかしながらよくよく考えてみるとyを0にしなくても似たような式変形により、
{ \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ \left( y-h \right) }^{ 2 }=0\\ \frac { { h }^{ 2 } }{ { r }^{ 2 } } { x }^{ 2 }+\frac { { h }^{ 2 } }{ { r }^{ 2 } } { z }^{ 2 }-{ \left( y-h \right) }^{ 2 }=0\\ \frac { 1 }{ { r }^{ 2 } } { x }^{ 2 }+\frac { 1 }{ { r }^{ 2 } } { z }^{ 2 }-\frac { { \left( y-h \right) }^{ 2 } }{ { h }^{ 2 } } =0\\ { x }^{ 2 }+{ z }^{ 2 }-{ r }^{ 2 }\frac { { \left( y-h \right) }^{ 2 } }{ { h }^{ 2 } } =0\\ { x }^{ 2 }+{ z }^{ 2 }={ r }^{ 2 }\frac { { \left( y-h \right) }^{ 2 } }{ { h }^{ 2 } } \\ { x }^{ 2 }+{ z }^{ 2 }={ \left( { r }\frac { y-h }{ { h } } \right) }^{ 2 }\\ { x }^{ 2 }+{ z }^{ 2 }={ \left( \frac { ry-rh }{ { h } } \right) }^{ 2 }\\ { x }^{ 2 }+{ z }^{ 2 }={ \left( \frac { r }{ h } y-r \right) }^{ 2 }\\ { x }^{ 2 }+{ z }^{ 2 }={ \left( -\frac { r }{ h } y+r \right) }^{ 2 }\\
これは結局、高さ y と 半径 r の関係性を表しており、大げさに関数Rで表すと、
R\left( y \right) =-\frac { r }{ h } y+r
結局これの意味する所は、
R\left( 0 \right) =-\frac { r }{ h } 0+r=r\\ R\left( h \right) =-\frac { r }{ h } h+r=0
と半径Rは、yが0のときに底面のrになり、y=hのとき0になり、なおかつ増加は線形であることを示しています。
確かにこれは高さ h, 底面の半径 r の 円錐の方程式だと言えます。
陰関数等位面の可視化
先の式変形によって式の意味は把握することができました。
ただ上記の円錐の方程式は、陰関数表現になっていますので、それをさくっとマーチングキューブ法などの方法で等位面をメッシュ化できれば便利そうです。
そこで最近ちょくちょく触り始めた Houdiniを使ってみます。
Houdiniはノードベースのプロシージャルな編集を得意とするCGソフトウェアです。最近結構流行ってきているみたいですね。Houdiniにも陰関数からメッシュを作成できるIsoSurfaceノードが使えるのでそれを試してみましょう。非商用利用版でも扱うことが可能です!
無料でもすぐに始めることができます。(回し者)
https://www.sidefx.com/ja/download/
デフォルトで配置されるfile1を削除しつつ、IsoSurfaceを選択して出します。
すると、すでにImplicit Functionに球の方程式が入力され、メッシュ化された状態で出現します!
方程式自体は、HScript、またはPythonで記述することができるそうです。
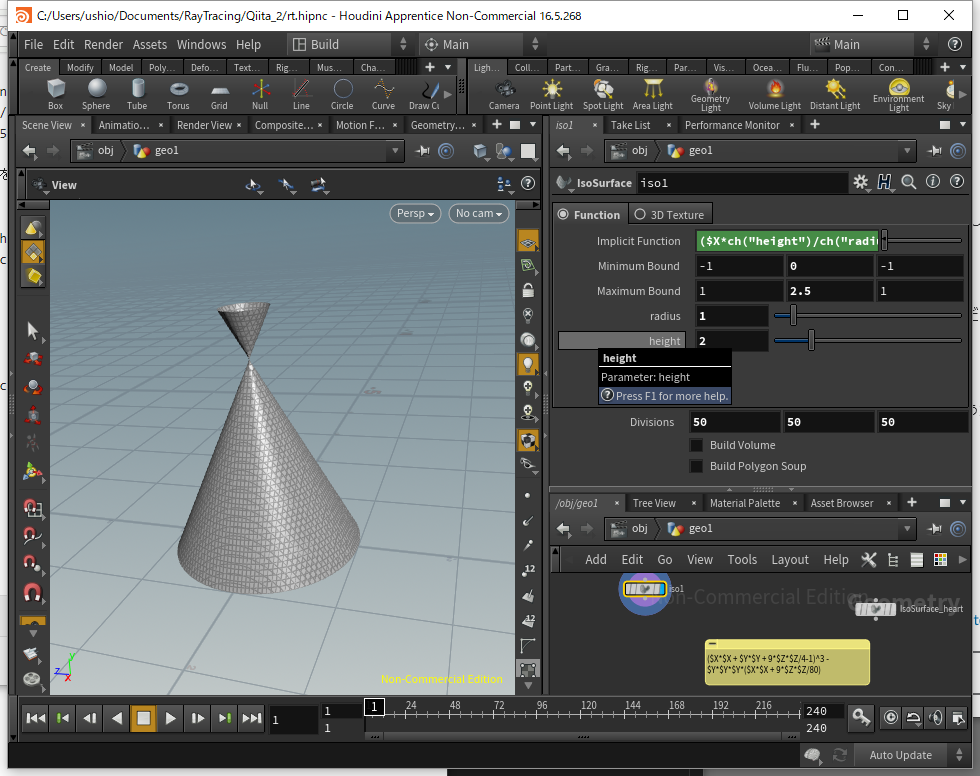
早速 r = 1, h = 2 の円錐を作ってみましょう。
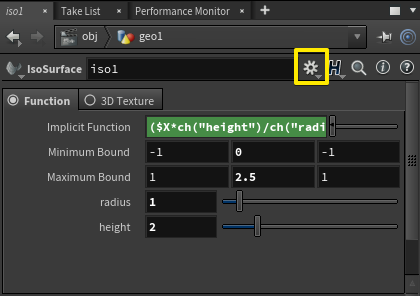
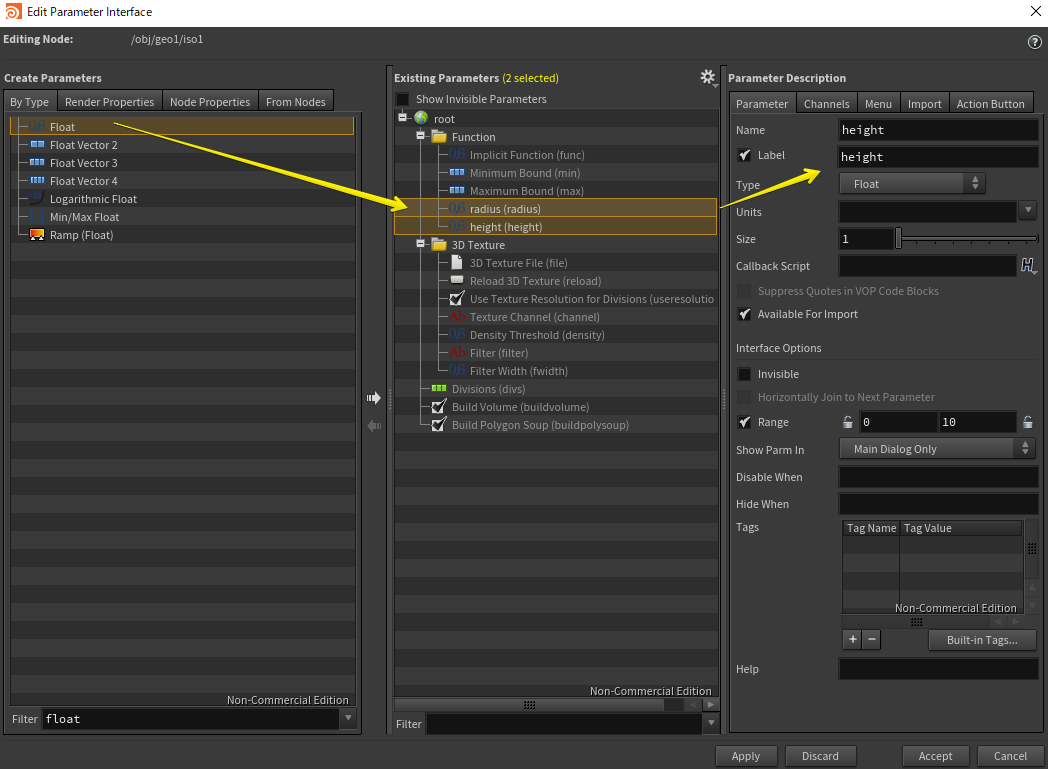
パラメータを指定するのに、インスペクタのギアアイコンから、Edit Parameter Interfaceを選ぶと、
また、パラメータ編集画面がでてきて、そこでheightとradiusを追加しておくと、Implicit Functionで参照できて大変便利です。
あとは式をそのままささっと書いてしまいます。
($X*ch("height")/ch("radius"))^2 + ($Z*ch("height")/ch("radius"))^2 - ($Y-ch("height"))^2
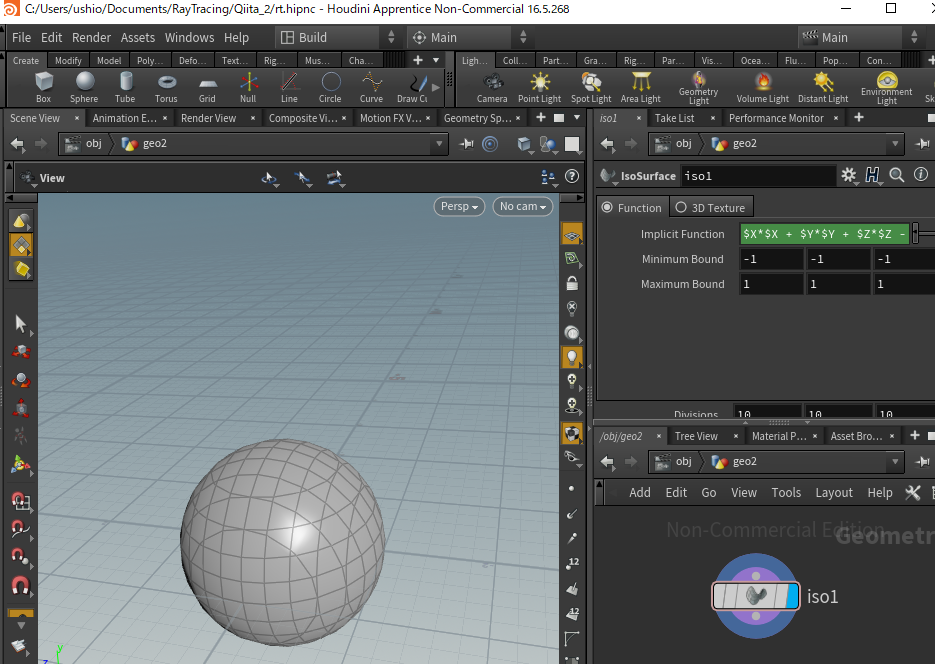
最後に座標の範囲を適当に決めて、分割数などを決めてあげれば、以下のように簡単にメッシュを作成できました!
おっと、可視化するとyがh以上の部分にも逆向きの円錐ができていることが見て取れます。この円錐の方程式が $ 0 <= y <= h $ でのみ定義されるというわけではないためですね。 不要な場合は実装のときにカットする必要がありそうです。
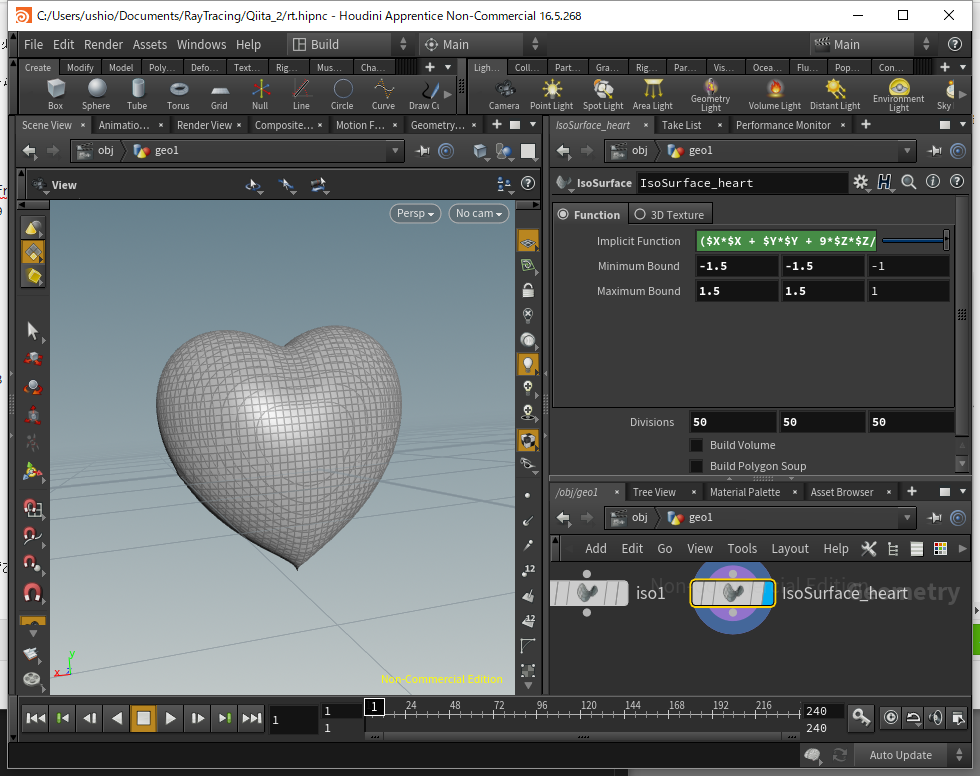
この方法は陰関数で定義できる表面なら簡単にビジュアライズできるため、例えば有名なハートの方程式
{ \left( { x }^{ 2 }+y^{ 2 }+\frac { 9 }{ 4 } z^{ 2 }-1 \right) }^{ 3 }-y^{ 3 }\left( { x }^{ 2 }+\frac { 9 }{ 80 } z^{ 2 } \right) = 0
も、
($X*$X + $Y*$Y + 9*$Z*$Z/4-1)^3 - $Y*$Y*$Y*($X*$X + 9*$Z*$Z/80)
と落とし込んでしまえば、
すぐビジュアライズすることができ、陰関数を対象に作業するとき、非常に強力な道具となってくれるでしょう。
光線との衝突判定
円錐と光線との衝突は、定番の方法である、図形の方程式に光線の方程式を代入してtについて解く方法で可能です。
{ \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ \left( y-h \right) }^{ 2 }=0\\ ray\left( t \right) =\left( o_{ x }+d_{ x }t,o_{ y }+d_{ y }t,o_{ z }+d_{ z }t \right) \\ \\ { \left( \frac { h\left( o_{ x }+d_{ x }t \right) }{ r } \right) }^{ 2 }+{ \left( \frac { h\left( o_{ z }+d_{ z }t \right) }{ r } \right) }^{ 2 }-{ \left( \left( o_{ y }+d_{ y }t \right) -h \right) }^{ 2 }=0\\ { \left( \frac { ho_{ x }+hd_{ x }t }{ r } \right) }^{ 2 }+{ \left( \frac { ho_{ z }+hd_{ z }t }{ r } \right) }^{ 2 }-{ \left( o_{ y }-h+d_{ y }t \right) }^{ 2 }=0\\ \frac { { \left( ho_{ x } \right) }^{ 2 }+2\left( ho_{ x }hd_{ x } \right) t+{ \left( hd_{ x } \right) }^{ 2 }{ t }^{ 2 } }{ { r }^{ 2 } } +\frac { { \left( ho_{ z } \right) }^{ 2 }+2\left( ho_{ z }hd_{ z } \right) t+{ \left( hd_{ z } \right) }^{ 2 }{ t }^{ 2 } }{ { r }^{ 2 } } -{ \left( o_{ y }-h \right) }^{ 2 }-2\left( o_{ y }-h \right) d_{ y }t-{ d_{ y } }^{ 2 }{ t }^{ 2 }=0\\ \frac { 1 }{ { r }^{ 2 } } \left( { \left( ho_{ x } \right) }^{ 2 }+2\left( ho_{ x }hd_{ x } \right) t+{ \left( hd_{ x } \right) }^{ 2 }{ t }^{ 2 }+{ \left( ho_{ z } \right) }^{ 2 }+2\left( ho_{ z }hd_{ z } \right) t+{ \left( hd_{ z } \right) }^{ 2 }{ t }^{ 2 } \right) -{ \left( o_{ y }-h \right) }^{ 2 }-2\left( o_{ y }-h \right) d_{ y }t-{ d_{ y } }^{ 2 }{ t }^{ 2 }=0\\ \frac { 1 }{ { r }^{ 2 } } \left( { \left( ho_{ x } \right) }^{ 2 }+{ \left( ho_{ z } \right) }^{ 2 }+2\left( ho_{ x }hd_{ x } \right) t+2\left( ho_{ z }hd_{ z } \right) t+{ \left( hd_{ x } \right) }^{ 2 }{ t }^{ 2 }+{ \left( hd_{ z } \right) }^{ 2 }{ t }^{ 2 } \right) -{ \left( o_{ y }-h \right) }^{ 2 }-2\left( o_{ y }-h \right) d_{ y }t-{ d_{ y } }^{ 2 }{ t }^{ 2 }=0\\ \frac { 1 }{ { r }^{ 2 } } \left( { { h }^{ 2 }\left( { o_{ x } }^{ 2 }+{ o_{ z } }^{ 2 } \right) }+2{ h }^{ 2 }\left( o_{ x }d_{ x }+o_{ z }d_{ z } \right) t+\left( \left( { hd_{ x } } \right) ^{ 2 }+{ \left( hd_{ z } \right) }^{ 2 } \right) { t }^{ 2 } \right) -{ \left( o_{ y }-h \right) }^{ 2 }-2\left( o_{ y }-h \right) d_{ y }t-{ d_{ y } }^{ 2 }{ t }^{ 2 }=0\\ \frac { { h }^{ 2 }\left( { o_{ x } }^{ 2 }+{ o_{ z } }^{ 2 } \right) }{ { r }^{ 2 } } +\frac { 2{ h }^{ 2 }\left( o_{ x }d_{ x }+o_{ z }d_{ z } \right) }{ { r }^{ 2 } } t+\frac { \left( { hd_{ x } } \right) ^{ 2 }+{ \left( hd_{ z } \right) }^{ 2 } }{ { r }^{ 2 } } { t }^{ 2 }-{ \left( o_{ y }-h \right) }^{ 2 }-2\left( o_{ y }-h \right) d_{ y }t-{ d_{ y } }^{ 2 }{ t }^{ 2 }=0\\ \left( \frac { { h }^{ 2 }\left( { o_{ x } }^{ 2 }+{ o_{ z } }^{ 2 } \right) }{ { r }^{ 2 } } -{ \left( o_{ y }-h \right) }^{ 2 } \right) +\left( \frac { 2{ h }^{ 2 }\left( o_{ x }d_{ x }+o_{ z }d_{ z } \right) }{ { r }^{ 2 } } -2\left( o_{ y }-h \right) d_{ y } \right) t+\left( \frac { { h }^{ 2 }\left( d_{ x }^{ 2 }+{ d_{ z } }^{ 2 } \right) }{ { r }^{ 2 } } -{ d_{ y } }^{ 2 } \right) { t }^{ 2 }=0
tの二次式になるので、あとは素直に解の公式を使って解けますね。
ちょっと長いので、
k=\frac { { h }^{ 2 } }{ { r }^{ 2 } }
とおくと、
\left( k\left( { o_{ x } }^{ 2 }+{ o_{ z } }^{ 2 } \right) -{ \left( o_{ y }-h \right) }^{ 2 } \right) +\left( 2k\left( o_{ x }d_{ x }+o_{ z }d_{ z } \right) -2\left( o_{ y }-h \right) d_{ y } \right) t+\left( k\left( d_{ x }^{ 2 }+{ d_{ z } }^{ 2 } \right) -{ d_{ y } }^{ 2 } \right) { t }^{ 2 }=0
ちょっとだけキレイになりました。
光線と円錐の衝突判定が、二次方程式の解に帰着するのは、交点が2点発生することから考えても自然ですね。
というわけでtminの扱いにだけ注意しつつ実装に落とし込むと、以下のような感じになるかとおもいます。円錐の上下を切れば、円錐台も表現可能です。
struct Cone {
double h = 1.0;
double r = 1.0;
double min_h = 0.0;
double max_h = 1.0;
};
inline double Sqr(double x) {
return x * x;
}
inline bool intersect_cone(Vec3 o, Vec3 d, Cone cone, double *tmin) {
double h = cone.h;
double r = cone.r;
double k = Sqr(h) / Sqr(r);
double a = k * (d.x * d.x + d.z * d.z) - d.y * d.y;
double b = 2.0 * k * (o.x * d.x + o.z * d.z) - 2.0 * (o.y - h) * d.y;
double c = k * (o.x * o.x + o.z * o.z) - Sqr(o.y - h);
double D = b * b - 4.0 * a * c;
if (D < 0.0) {
return false;
}
double t;
bool isect = false;
double sqrt_D = std::sqrt(D);
t = (-b + sqrt_D) / (2.0 * a);
if (0.0 < t && t < *tmin) {
double y = o.y + d.y * t;
if (cone.min_h <= y && y <= cone.max_h) {
*tmin = t;
isect = true;
}
}
t = (-b - sqrt_D) / (2.0 * a);
if (0.0 < t && t < *tmin) {
double y = o.y + d.y * t;
if (cone.min_h <= y && y <= cone.max_h) {
*tmin = t;
isect = true;
}
}
return isect;
}
あとは回転させたり、移動させたりする処理は光線の前処理として実装すれば良いです。
ただ制御点2点と、そのそれぞれの半径で指定するような実装をしたい場合、ちょっとだけ工夫が必要で、rの差が2点で非常に近い場合は円錐でなく円筒で別途計算しないと、hが無限に大きくなってしまう関係上、うまくいきませんので、注意が必要です。
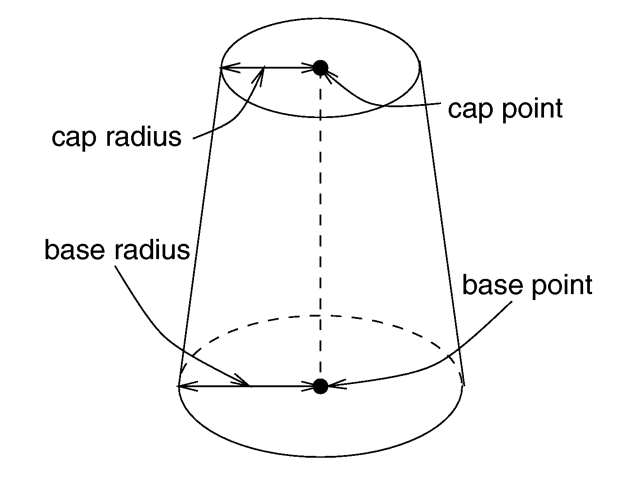
http://www.povray.org/documentation/view/3.7.0/277/
より
円筒の場合も同様に、
{ \left( x \right) }^{ 2 }+{ \left( z \right) }^{ 2 }-{ r }^{ 2 }=0\\ { \left( o_{ x }+d_{ x }t \right) }^{ 2 }+{ \left( o_{ z }+d_{ z }t \right) }^{ 2 }-r^{ 2 }=0\\ { o_{ x } }^{ 2 }+2o_{ x }d_{ x }t+{ d_{ x } }^{ 2 }{ t }^{ 2 }+{ o_{ z } }^{ 2 }+2o_{ z }d_{ z }t+d_{ z }^{ 2 }{ t }^{ 2 }-r^{ 2 }=0\\ \left( { o_{ x } }^{ 2 }+{ o_{ z } }^{ 2 }-r^{ 2 } \right) +\left( 2o_{ x }d_{ x }+2o_{ z }d_{ z } \right) t+\left( { d_{ x } }^{ 2 }+{ d_{ z } }^{ 2 } \right) { t }^{ 2 }=0
とすれば良いでしょう。
POV-Rayの実装も参考になります。
https://github.com/POV-Ray/povray/blob/master/source/core/shape/cone.cpp
法線
衝突点の他に法線もやはり必要になります。なのでそれを求めます。
上記の円錐の陰関数は、スカラー場を表しますので、等位面の法線は勾配によりもとめることができます。
f\left( x,y,z \right) ={ \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ \left( y-h \right) }^{ 2 }\\ n=normalize\left( \left\{ \frac { \partial }{ \partial x } f\left( x,y,z \right) ,\frac { \partial }{ \partial y } f\left( x,y,z \right) ,\frac { \partial }{ \partial z } f\left( x,y,z \right) \right\} \right) \\ n=normalize\left( grad\quad f\left( x,y,z \right) \right)
ところでこのことは、ベクトル解析の初歩のところで書いてあるのをよく見かけますが、これは何故でしょうか?
これは例えば丁度円錐上の点を1点考えて、その時点で $ f \left( x,y,z \right)=0 $ だったとします。そこで、ちょっとだけ移動する、つまり $ \left(\Delta x, \Delta y, \Delta z \right) $ だけ移動させることを考えます。すると、どのくらい $ f \left( x,y,z \right) $ の値が変化するかといえば、
\frac { \partial f\left( x,y,z \right) }{ \partial x } \Delta x+\frac { \partial f\left( x,y,z \right) }{ \partial y } \Delta y+\frac { \partial f\left( x,y,z \right) }{ \partial z } \Delta z
の分だけ変化します。このような考え方は全微分というのでした。
ところでこの "ちょっとだけの移動" が、円錐表面上の移動だったとしたら、このfの変化量はゼロになるはずです。
\frac { \partial f\left( x,y,z \right) }{ \partial x } \Delta x+\frac { \partial f\left( x,y,z \right) }{ \partial y } \Delta y+\frac { \partial f\left( x,y,z \right) }{ \partial z } \Delta z=0
ここで式をよく見ると、これはベクトル同士の内積とも解釈することができます。
\left( \frac { \partial }{ \partial x } f\left( x,y,z \right) ,\frac { \partial }{ \partial y } f\left( x,y,z \right) ,\frac { \partial }{ \partial z } f\left( x,y,z \right) \right) \cdot \left( \Delta x,\Delta y,\Delta z \right) =0
先程"ちょっとだけの移動" が、円錐表面上の移動を仮定しました。そして内積が0になるのは2つのベクトルが直交している場合です。したがって、$ \left( \frac { \partial }{ \partial x } f\left( x,y,z \right) ,\frac { \partial }{ \partial y } f\left( x,y,z \right) ,\frac { \partial }{ \partial z } f\left( x,y,z \right) \right) $ というベクトルは表面の移動と直交するベクトルであることがわかり、そしてそれは常に法線である、というわけです。ただこの場合向きについては考慮していないことには注意しましょう。
よくレイマーチングの手法でも偏微分で法線を求める方法が紹介されていますが、距離関数による図形もやはりスカラー場の等位面であり、同様の考え方であるといえます。
では実際に偏微分を求めてみます。
f\left( x,y,z \right) ={ \left( \frac { hx }{ r } \right) }^{ 2 }+{ \left( \frac { hz }{ r } \right) }^{ 2 }-{ \left( y-h \right) }^{ 2 }\\ f\left( x,y,z \right) =\frac { { h }^{ 2 } }{ { r }^{ 2 } } { x }^{ 2 }+\frac { { h }^{ 2 } }{ { r }^{ 2 } } { z }^{ 2 }-{ \left( y-h \right) }^{ 2 }\\ \\ \frac { \partial f\left( x,y,z \right) }{ \partial x } =2\frac { { h }^{ 2 } }{ { r }^{ 2 } } x\\ \frac { \partial f\left( x,y,z \right) }{ \partial z } =2\frac { { h }^{ 2 } }{ { r }^{ 2 } } z\\ \frac { \partial f\left( x,y,z \right) }{ \partial y } =2\left( y-h \right)
実装は例えば以下のようになります。
inline Vec3 gradient_cone(Vec3 p, Cone cone) {
double hh_over_rr = cone.h * cone.h / (cone.r * cone.r);
double dfdx = 2.0 * hh_over_rr * p.x;
double dfdy = 2.0 * (cone.h - p.y);
double dfdz = 2.0 * hh_over_rr * p.z;
return Vec3(dfdx, dfdy, dfdz);
}
ただ定数の部分はどうせ後でベクトルの正規化が走るため、2倍する部分は削った実装もありだと思います。
法線のビジュアライズ
先の陰関数等位面の可視化のパートでhoudiniを使って可視化する方法を紹介しましたが、法線も結構簡単にビジュアライズすることができます。
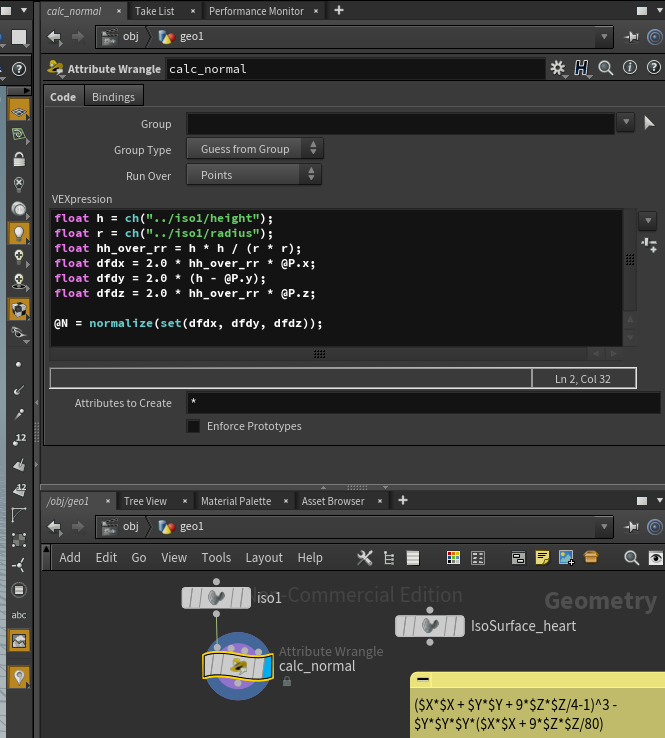
それには、先に作成したIsoSurfaceノードから、RunOverをPointsにしたAttribute Wrangleを記述します。
こちらはVEXという言語です。
結構C系列にシンタックスが似ているので、書くのにさほど苦労はないでしょう。
float h = ch("../iso1/height");
float r = ch("../iso1/radius");
float hh_over_rr = h * h / (r * r);
float dfdx = 2.0 * hh_over_rr * @P.x;
float dfdy = 2.0 * (h - @P.y);
float dfdz = 2.0 * hh_over_rr * @P.z;
@N = normalize(set(dfdx, dfdy, dfdz));
ch("../iso1/height"); のように記述すれば、ディレクトリをたどるようにパラメータにアクセス可能で便利です。
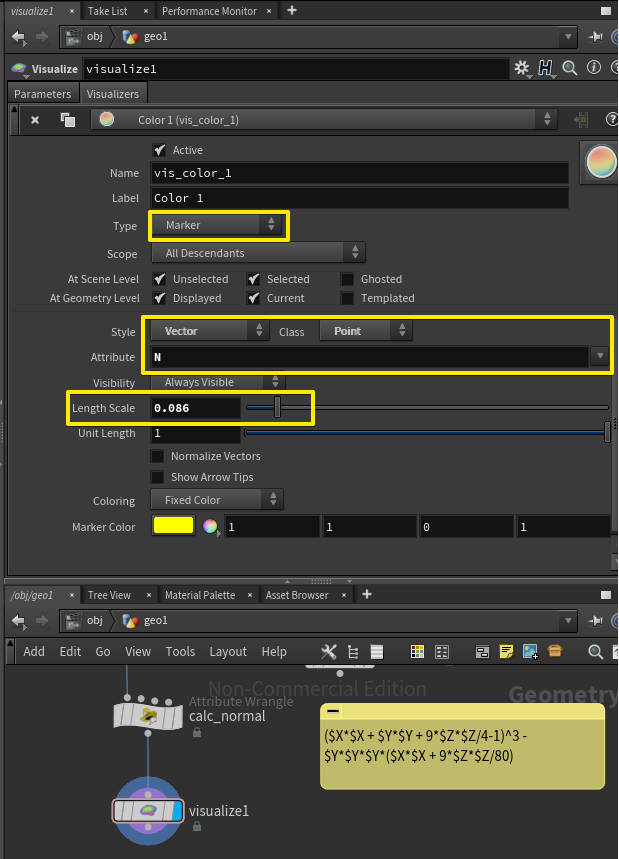
そしてVisualizeというその名もずばりなパッチをその後続につなぎます。
そしてTypeをMarker、StyleをVectorに、AttributeをNにすれば、法線を可視化することが可能です。
どうやら結構うまく計算できているようです。
まとめ
今回はちょっとマイナーな図形に対するTipsでしたが、Houdiniを使うことで本質的な部分のプログラミングにだけ集中しよう、というミニテーマをかかげつつ書いてみました。
すべてプログラミングで解决しようとするとそこそこ面倒なコードを書かなければならないところを、結構労力を節約できたのではないでしょうか。こういうったツールもうまく活用しつつ、思考を加速させていきたいものです。
Houdiniでプログラミングをしてみたい方におすすめです
理論と実践で学ぶHoudini -SOP&VEX編
https://www.amazon.co.jp/o/ASIN/4862463592/bdbooks-22
※今回使用したHoudiniのバージョンは、16.5.268になります