弦の運動を考える
今回は手始めに弦の運動を考えます。
いきなり空間的な運動を考えるのは大変なので、この弦は上下にしか運動しないことにします。
それを踏まえて、もろもろ現実との対応を考えます。
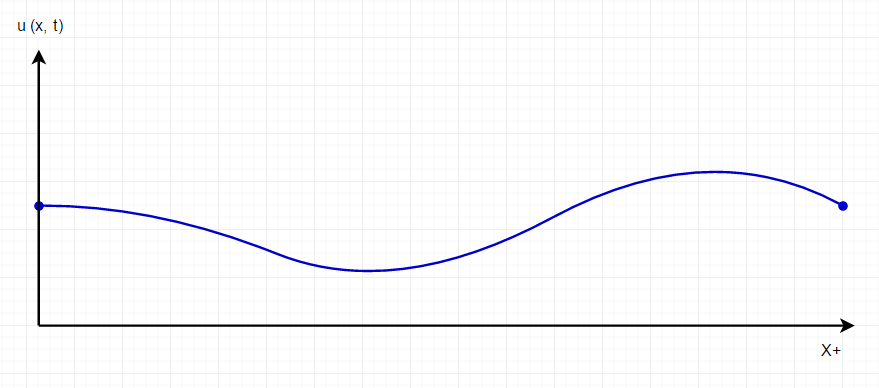
図のように弦が左から右に貼られている状況で、ある時間 (t) におけるある位置 (x) における弦の高さを **u(x, t)**と関数として捉えることにします。
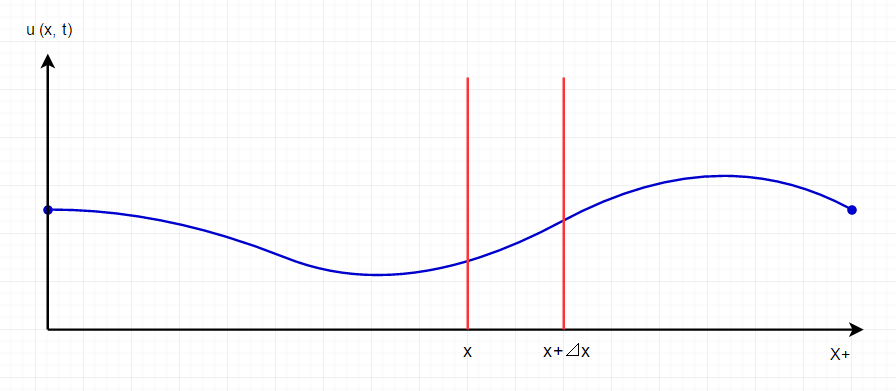
さて、次にこの弦の空間を細切れにして、ある地点xとそこから微小な距離⊿xだけ離れた x+⊿xに挟まれる弦について考えます。
また、弦にはわずかながら質量がありますので、質量を考えたいですが、細切れにすることを考えると、密度を考えたほうが都合が良さそうです。そこで今回は弦の長さあたりの質量をρとおきます。
とすると、この⊿xの長さの弦の質量は、ρ⊿xとして扱う事ができます。
次にこの微小弦に働く力を考えます。
まず重力が考えられますが、今回は真上から弦を観察することにして、重力を無視します。あしからず。
重力を考えないとなると、次は張力を考えます。
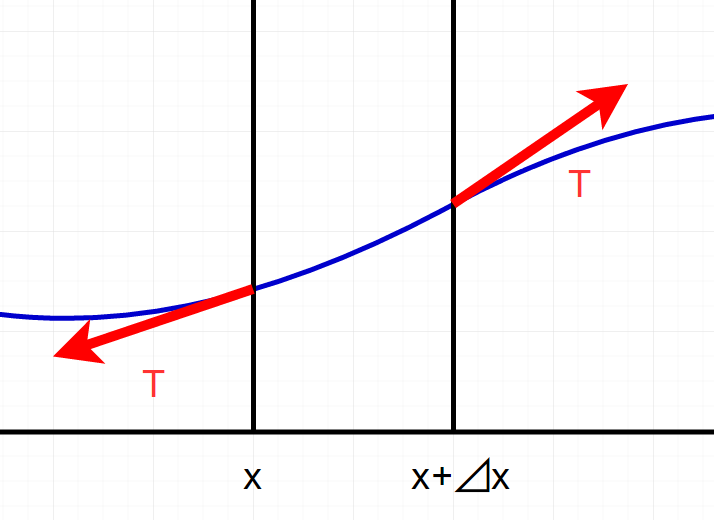
微小弦は左端と右端で、共にある張力(T)で常に引っ張られていると考えます。
今回弦は上下にしか運動しないことにしました。
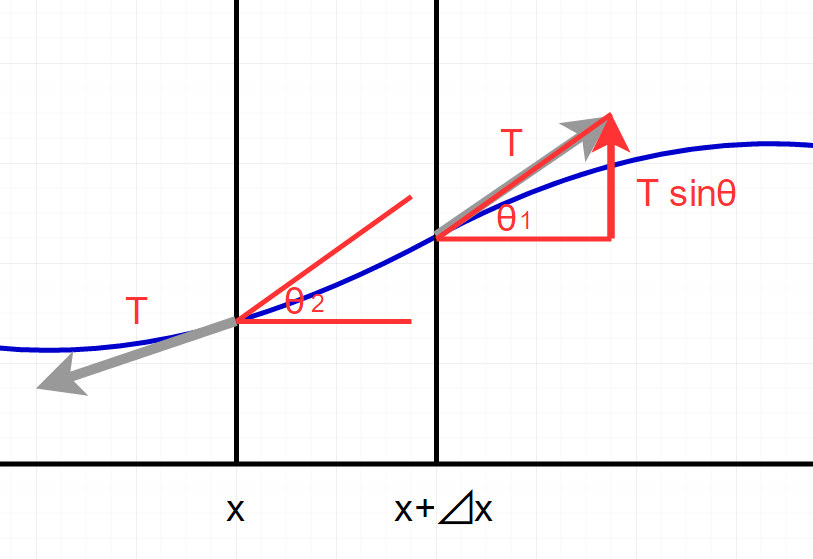
弦の角度を右をθ1、左がθ2、としておいたとき、張力Tがu(x, t)に影響する成分は図を参考に、
右側(x+⊿x) = T\sin{\theta_1}\\
左側(x) = -T\sin{\theta_2}\\
となります。
したがって、ここまでの考察をもとに、弦の運動方程式ma=Fを以下のように立てます。
ρ⊿x\frac { { \partial }^{ 2 }u\left( x,t \right) }{ { \partial }{ t }^{ 2 } } =T\sin { \theta _{ 1 } } -T\sin { \theta _{ 2 } }
さて、ここでそれぞれの角度がとても小さいと仮定します。なので、
\sin \theta =\frac { \sin { \theta } }{ \cos { \theta } } \cos { \theta } =\tan { \theta } \cos { \theta } =\frac { \partial u(x,t) }{ \partial x } \cos { \theta } \cong \frac { \partial u(x,t) }{ \partial x }
のように考えることができます。
それを元に、
ρ⊿x\frac { { \partial }^{ 2 }u\left( x,t \right) }{ { \partial }{ t }^{ 2 } } =T(\sin { \theta _{ 1 } } -\sin { \theta _{ 2 } } )\\ ρ⊿x\frac { { \partial }^{ 2 }u\left( x,t \right) }{ { \partial }{ t }^{ 2 } } =T(\frac { \partial u(x+⊿x,t) }{ \partial x } -\frac { \partial u(x,t) }{ \partial x } )\\ \frac { { \partial }^{ 2 }u\left( x,t \right) }{ { \partial }{ t }^{ 2 } } =\frac { T }{ ρ } (\frac { \frac { \partial u(x+⊿x,t) }{ \partial x } -\frac { \partial u(x,t) }{ \partial x } }{ ⊿x } )\\ \frac { { \partial }^{ 2 }u\left( x,t \right) }{ { \partial }{ t }^{ 2 } } =\frac { T }{ ρ } \frac { { \partial }^{ 2 }u(x,t) }{ { \partial }{ x }^{ 2 } }
と一般的な波動方程式の形まで持っていく事ができました。
コンピュータでの数値解法についてはこちら
http://qiita.com/Ushio@github/items/0249fd7a5363ccd914dd