懸垂線(カテナリー曲線)
懸垂線とはあまり伸びないロープやチェーンなどの端を、2点固定してぶら下げてできる曲線です。
これの何が面白いかというと、この曲線が大変シンプルな数式で表せる所にあります。
結論から述べてしまうと以下の式がこの曲線を表現しているというのです。
f\left( x \right) =a\cosh { \left( \frac { x }{ a } \right) }
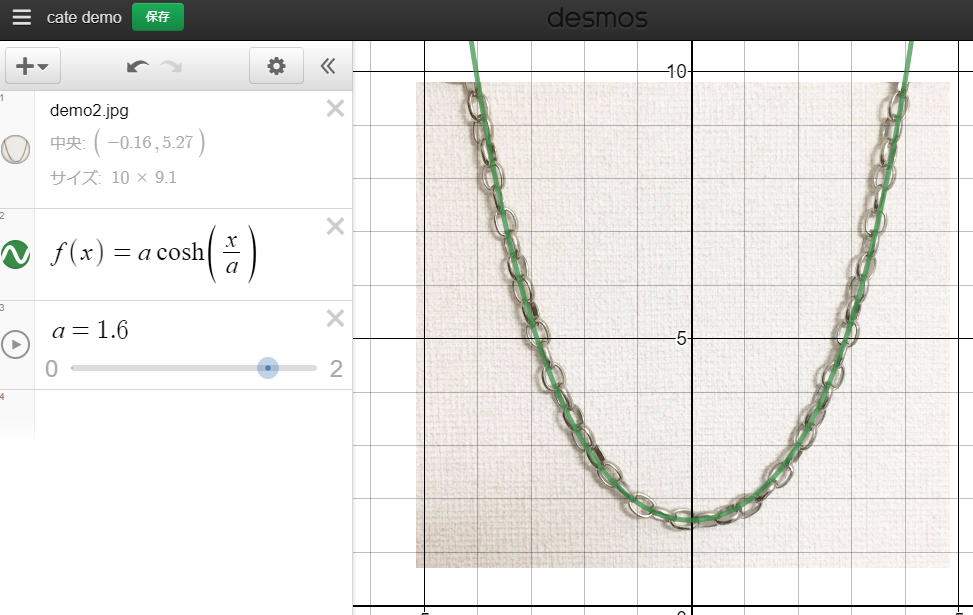
実際に写真に重ねてみると(desmosは便利ですね!)、
おお、たしかに現実の物理現象と大変よくマッチしています。
実際のところわりとこのトピックは語り尽くされた内容ではありますが、
この記事では、
- 一体どこからこの関数がやってきたのか?
- コンピュータグラフィックスで懸垂線を扱うには?
というのを個人的に興味がある数学と一緒に学んでみたいと思います。
プログラミングにはC++を使うことにします。
この関数はどこから来るの?
実のところ、この懸垂線の関数の導出には調べてみるとたくさんアプローチがあります。今回はそのうち自分の好きなやり方を一つ紹介します。
まず紐全体の力学的エネルギー $ E $を考えます。
E=\frac { 1 }{ 2 } m{ v }^{ 2 }+mgh
※h は高さ、m が質量、vが速度です。
しかしながら今回はひもは運動しておらず、速度は常にゼロであります。
これで力学的エネルギーはかなりシンプルになります。
E=mgh
ここでひもの質量の表現として、長さあたりの質量として、$ \rho $ を一応定義しておきます。
例えば$ \rho $がすべての場所で同じ紐の場合、長さsメートルの紐の質量wは、
w=s\rho
となるような量です。
ここで紐の長さについても考えておきましょう。
ある地点 $ x $ における紐の高さを関数 $ y\left( x \right) $ で考えることにして、長さを求めるにはやはり細かく区間を区切って合計する必要がありそうです。
微小な長さは、
と三平方の定理で求めることができるため、微小な長さ $ \Delta s $ は、
\Delta s=\sqrt { \left( \Delta x \right) ^{ 2 }+\left( \Delta y \right) ^{ 2 } } \\ =\sqrt { \left( \Delta x \right) ^{ 2 }+\left( \Delta x\dot { y } \left( x \right) \right) ^{ 2 } } \\ =\sqrt { \left( \Delta x \right) ^{ 2 }+\left( \Delta x \right) ^{ 2 }\left( \dot { y } \left( x \right) \right) ^{ 2 } } \\ =\sqrt { \left( \Delta x \right) ^{ 2 }\left( 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } \right) } \\ =\sqrt { 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } } \Delta x
と考えることができるため、あとはこれをxを細かくしていって、足し合わせます。
すると長さsは、
s=\sum _{ i=1 }^{ n }{ \sqrt { 1+\left( \dot { y } \left( x_{ i } \right) \right) ^{ 2 } } \Delta x_{ i } } \\ s=\int _{ a }^{ b }{ \sqrt { 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } } dx }
と記述することができます。
さて、長さが求め方がわかれば、あとは微小な部分の位置エネルギーを合計して全体の位置エネルギーにすれば良いですね
E=\int _{ a }^{ b }{ mgh } dx\\ E=\int _{ a }^{ b }{ \rho \sqrt { 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } } gy\left( x \right) dx } \\ E=\int _{ a }^{ b }{ \rho gy\left( x \right) \sqrt { 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } } dx }
ところで、先に"紐は運動していない"ことにしました。その為紐のもつ力学的エネルギーは、すべて位置エネルギーであり、例えばもしちょっと紐に余裕があり、運動エネルギーに変換されてしまう余地があったとしたら、きっと運動が始まってしまうでしょう。したがって、安定した紐においては、この $ E $ が最小化されるような $ y\left( x \right) $ がきっと懸垂線を表しているのではないでしょうか
E を最小化する関数
しかし最小化する、と簡単に言ってもEの積分方程式の中には$ y\left( x \right) $ や $ \dot { y } \left( x \right) $ が複雑に絡み合っていて、一筋縄ではいかなそうです。
しかしこれをなんとも不思議に解いてしまう方法がとうの昔(1696年?)に発見されており、それは変分法というものらしいです。
ともかくそれにならって考えてみます。
先のEの具体的な形を作り出したものの、いったん抽象化して考えてみると、Eの値というのは関数を受け取って数値が確定する関数だと考える事ができます。
※$ \rho g $が鬱陶しいのでそれを消去するIを代わりに考えます。低数倍なので全体の最小化を考えるときにはなんら問題無いでしょう。ここからは代わりにIの最小化を考えます。
E=\rho g\int _{ a }^{ b }{ y\left( x \right) \sqrt { 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } } dx } \\ \frac { E }{ \rho g } =\int _{ a }^{ b }{ y\left( x \right) \sqrt { 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } } dx } \\ I=\frac { E }{ \rho g } \\ I=\int _{ a }^{ b }{ f\left( x,y,\dot { y } \right) dx } \\ f\left( x,y,\dot { y } \right) =y\left( x \right) \sqrt { 1+\left( \dot { y } \left( x \right) \right) ^{ 2 } }
Iはもはや関数を受け取る関数と捉えることもでき、こういった関数を汎関数と呼びます。
いやいや、$ y \left( x \right) $ と $ \dot { y } \left( x \right) $ には関数と導関数の関係があるのだから、受け取る関数など一つではないか!と怒られそうですが、$ f $ の中にそういった操作を入れ込むよりも、割り切って分けておいたほうが後々楽になるのです。
ところでこのような関数を受け取る関数、プログラミングの文脈で考えるとなにも特別な話でもなく、例えばC++での擬似コードで、
# include <functional>
double I(double a, double b, std::function<double(double)> y, std::function<double(double)> dydx) {
int N = 100;
double dx = (b - a) / N;
double sum = 0;
for (int i = 0; i < N; ++i) {
double x = a + dx * i;
double dydx_value = dydx(x);
sum += y(x) * std::sqrt(1.0 + dydx_value * dydx_value) * dx;
}
return sum;
}
といったのをイメージすると、コードの方が慣れている方にとってはとっつきやすいかもしれません。
ここでIが最小となるような $ y\left( x \right) $ をどこかから引き当てたとしてその時状況を想像します。
そして、対象範囲でちょっとこの関数に"パテ盛り"をして若干ずらす分 $ \delta y \left(x \right) $ を考えます。
ただし、
\delta y\left( a \right) =0\\ \delta y\left( b \right) =0
ようは端っこではパテ盛りしない、ということにします。
そんなわけでパテ盛りした $ I $ というのを考えますと、
I+\delta I=\int _{ a }^{ b }{ f\left( x,y+\delta y,\dot { y } +\delta \dot { y } \right) dx }
と表現できます。
ただ、数式では最初はちょっとイメージしずらいので、擬似コードを考えてみると、
double E = I(0, 10, function_y, function_dydx);
double E_plus_deltaE = I(0, 10, [](double x) {
return function_y(x) + function_delta_y(x);
}, [](double x) {
return function_dydx(x) + function_delta_dydx(x);
});
という操作です。
おっと、 $ \delta y \left(x \right) $ を増やしただけなのに、微分の部分にも変化が起きています。これはなぜかといえば、元の $ y\left( a \right) $ に増分が発生しているので、当然その勾配にも変化が発生し、その勾配の増分というもやはり積み上がるものだからです。
イメージは以下のようなかんじです。
あれ、でもこれって落ち着いてみると、"微分の和は、和の微分"、ということですね。
とにかくこれで関数をちょっと変化させたときの量を考えることができるようになってきました。
ただ実際のところこの"微小なパテ盛り"は思考実験であり、後に0にすることを考えます。
次は $ I+\delta I $ という量をもうちょっとスマートにしてしまいましょう。
I+\delta I=\int _{ a }^{ b }{ f\left( x,y+\delta y,\dot { y } +\dot { \delta y } \right) dx } \\ \delta I=\int _{ a }^{ b }{ f\left( x,y+\delta y,\dot { y } +\dot { \delta y } \right) dx } -I\\ \delta I=\int _{ a }^{ b }{ f\left( x,y+\delta y,\dot { y } +\dot { \delta y } \right) dx } -\int _{ a }^{ b }{ f\left( x,y,\dot { y } \right) dx } \\ \delta I=\int _{ a }^{ b }{ \left\{ f\left( x,y+\delta y,\dot { y } +\dot { \delta y } \right) -f\left( x,y,\dot { y } \right) \right\} dx }
ここで、
f\left( x,y+\delta y,\dot { y } +\delta \dot { y } \right) -f\left( x,y,\dot { y } \right)
というのはどんな量なのでしょうか?
実際のところ、具体的な $ y\left( x \right), \dot { y } \left( x \right), \delta y,\dot { \delta y } \left( x \right) $ 達が決まれば、これは単なる数値でしかありません。関数を受け取る関数、というとなんだか混乱してしまいますが、多変数関数のテイラー展開を思い出して、
f\left( x+\Delta x,y+\Delta y \right) -f\left( x,y \right) =\frac { \partial f\left( x,y \right) }{ \partial x } \Delta x+\frac { \partial f\left( x,y \right) }{ \partial y } \Delta y+...
受け取る関数の返す数値がどれだけ増えるのか?減るのか?を考えてあげれば良く、これはまさに $ y\left( x \right) $ などをただの変数かのごとく微分操作をすれば良いということです。
というわけで、
f\left( x,y+\delta y,\dot { y } +\delta \dot { y } \right) -f\left( x,y,\dot { y } \right) =\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta y+\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \dot { \delta y }
になるため、先の$ \delta I $ は、
\delta I=\int _{ a }^{ b }{ \left\{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta y+\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \dot { \delta y } \right\} dx }
となります。
ちょっと抽象的になってしまったので、感覚を取り戻すために、試しに具体的な形を一応思い出してみます。$ f $ は、
f\left( x,y,\dot { y } \right) =y\left( x \right) \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } }
だったので、
\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } =\sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } \\ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } =\frac { \partial }{ \partial \dot { y } } \left\{ y\left( x \right) { \left( 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } \right) }^{ \frac { 1 }{ 2 } } \right\} \\ =y\left( x \right) \frac { 1 }{ 2 } { \left( 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } \right) }^{ -\frac { 1 }{ 2 } }\frac { \partial }{ \partial \dot { y } } \left( 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } \right) \\ =y\left( x \right) \frac { 1 }{ 2 } { \left( 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } \right) }^{ -\frac { 1 }{ 2 } }2\dot { y } \left( x \right) \\ =y\left( x \right) { \left( 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } \right) }^{ -\frac { 1 }{ 2 } }\dot { y } \left( x \right) \\ =\frac { y\left( x \right) \dot { y } \left( x \right) }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } }
$ \dot { y } \left( x \right) $ と微分がついている関数に対してこんな操作をするのは最初は戸惑ってしまうかもしれませんが、関数を受け取る時点でfの内部としては別な関数として扱っていることを思い出しますと、fの立場的にはそれの中身はなんでもよく、$ \dot { y } \left( x \right) $ だろうが、$ y \left( x \right) $ のように微分と積分の関係があろうがなかろうがどうでも良い、と考えると良いかもしれません。
話を戻しまして、 $ \delta I $ をもうちょっと操作してみましょう
\delta I=\int _{ a }^{ b }{ \left[ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta y+\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \dot { \delta y } \right] dx } \\ \delta I=\int _{ a }^{ b }{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta ydx } +\int _{ a }^{ b }{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \dot { \delta y } dx }
ここで部分積分を適用します。
\delta I=\int _{ a }^{ b }{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta ydx } +\left[ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \delta y \right] _{ a }^{ b }-\int _{ a }^{ b }{ \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \delta ydx }
次に
\delta y\left( a \right) =0\\ \delta y\left( b \right) =0
と約束したのを思い出すと、真ん中の項は0になることがわかります
\delta I=\int _{ a }^{ b }{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta ydx } +\left[ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \delta y \right] _{ a }^{ b }-\int _{ a }^{ b }{ \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \delta ydx } \\ \delta I=\int _{ a }^{ b }{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta ydx } +\left( \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \left( b \right) \cdot \delta y\left( b \right) -\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \left( a \right) \cdot \delta y\left( a \right) \right) -\int _{ a }^{ b }{ \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \delta ydx } \\ \delta I=\int _{ a }^{ b }{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta ydx } +\left( \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \left( b \right) \cdot 0-\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \left( a \right) \cdot 0 \right) -\int _{ a }^{ b }{ \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \delta ydx } \\ \delta I=\int _{ a }^{ b }{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta y\left( x \right) dx } -\int _{ a }^{ b }{ \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \delta y\left( x \right) dx } \\ \delta I=\int _{ a }^{ b }{ \left\{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \delta y\left( x \right) -\left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \delta y\left( x \right) \right\} dx } \\ \delta I=\int _{ a }^{ b }{ \left\{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } -\left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \right\} \delta y\left( x \right) dx }
そして、この$ \delta I $ を 0とおきます。
\delta I=\int _{ a }^{ b }{ \left\{ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } -\left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \right\} \delta y\left( x \right) dx }=0
ちょっと"パテ盛り"したときの変化がゼロ、 $ y\left( x \right) $ をどっちにパテ盛りしても値が変化しない、これは局所的かもしれないが、その付近では $ I $が極大か極小になっていることを意味します。
これは関数の微分をゼロとおいて極大極小点を見つけるのと同様の考え方になります。
すると更に、任意の"パテ盛り"に対して、$ \delta I = 0 $ となるためには、範囲すべての $ x $で、
\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } -\left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) =0
が成り立たなければならないことがわかります。
もうちょっと短く書いて、
\frac { \partial f }{ \partial y } -\frac { d }{ dx } \frac { \partial f }{ \partial \dot { y } } =0
を **オイラー・ラグランジュ方程式 (Euler - Lagrange equation)**と呼びます。
つまり$ I $ を極小にするような $ y\left( x \right) $ を見つけるということは、この方程式を満たす$ y\left( x \right) $ を探すことと言い換えることができます。※極小か極大かの議論は必要ですが・・
懸垂線の式を求めようとしてはいましたが、オイラー・ラグランジュ方程式は、懸垂線だけでなく幅広い問題に対して適用することのできる非常に汎用的な方程式です。(自分はたいして使い倒したことも無いので、実はあまり大きなことは言えないのですが・・・)
解析力学やら、量子力学には数多く応用されていると聞きます。
ベルトラミの公式
さて、いきなりオイラー・ラグランジュ方程式に先のfをぶち込んでみてもいいのですが、あらかじめちょっと変形しておくと後の式変形が楽になる場合があります。
例えば今回の場合、元のfがどういうものだったかというと、
f\left( x,y,\dot { y } \right) =y\left( x \right) \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } }
よくよく見ると、$ x $ の値は直接的に使われておらず、かならず 引数である関数を経由しています。このことを利用するとオイラー・ラグランジュ方程式がもうちょっと簡単になります。
まずオイラー・ラグランジュ方程式の両辺に $\dot { y } $ をかけます。
\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } =\left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \\ \dot { y } \cdot \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } =\dot { y } \cdot \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \cdots \left( A \right)
次に、$ f $ の $ x $ 微分について考えてみると、繰り返しになりますが、$ x $ の値は直接的に使われておらず、かならず引数である $ y,\dot { y } $ を経由します。
これを利用すると、これは多変数関数の微分のチェーンルールを適用できます。
\frac { d }{ dx } f\left( x,y,\dot { y } \right) =\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \cdot \frac { dy }{ dx } +\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \frac { d\dot { y } }{ dx } \\ \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } \cdot \frac { dy }{ dx } =\frac { d }{ dx } f\left( x,y,\dot { y } \right) -\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \frac { d\dot { y } }{ dx } \\ \dot { y } \cdot \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial y } =\frac { d }{ dx } f\left( x,y,\dot { y } \right) -\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \frac { d\dot { y } }{ dx } \cdots \left( B \right)
ここで (B) - (A) を考えてみると、
0=\frac { d }{ dx } f\left( x,y,\dot { y } \right) -\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \frac { d\dot { y } }{ dx } -\dot { y } \cdot \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \\ \frac { d }{ dx } f\left( x,y,\dot { y } \right) =\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \frac { d\dot { y } }{ dx } +\dot { y } \cdot \left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \\ \frac { d }{ dx } f\left( x,y,\dot { y } \right) =\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \frac { d\dot { y } }{ dx } +\left( \frac { d }{ dx } \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) \cdot \dot { y }
おっと、よくよく見ると、右辺は積の微分公式の形をしています。なので、
\frac { d }{ dx } f\left( x,y,\dot { y } \right) =\frac { d }{ dx } \left( \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \dot { y } \right) \\ \frac { d }{ dx } f\left( x,y,\dot { y } \right) -\frac { d }{ dx } \left( \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \dot { y } \right) =0\\ \frac { d }{ dx } \left( f\left( x,y,\dot { y } \right) -\frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \cdot \dot { y } \right) =0\\ \frac { d }{ dx } \left( f\left( x,y,\dot { y } \right) -\dot { y } \cdot \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } \right) =0
あとは両辺を $ x $ で積分すれば、
f\left( x,y,\dot { y } \right) -\dot { y } \cdot \frac { \partial f\left( x,y,\dot { y } \right) }{ \partial \dot { y } } =C
と、この方程式をベルトラミの公式と呼びます。
いくつか場面に応じて変形パターンがたくさんあるようですが、全部やるのは骨が折れるので、今回はベルトラミの公式だけです。。興味のある方は以下のリンクを参照のこと・・・
"物理のかぎしっぽ 変分法2"
http://hooktail.sub.jp/mathInPhys/variations2/
懸垂線を求める
では先程得られたベルトラミの公式を使って、懸垂線に迫っていきます
先に偏微分を整理しておきましょう
f\left( x,y,\dot { y } \right) =y\left( x \right) \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } \\ \frac { \partial f }{ \partial y } =\sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } \\ \frac { \partial f }{ \partial \dot { y } } =\frac { y\left( x \right) \dot { y } \left( x \right) }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } }
一気に代入していくと、
f\left( y,\dot { y } \right) -\dot { y } \frac { \partial f }{ \partial \dot { y } } =constant\\ \\ y\left( x \right) \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } -\dot { y } \frac { y\left( x \right) \dot { y } \left( x \right) }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } =a\\ y\left( x \right) \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } -\frac { { y\left( x \right) { \left( \dot { y } \left( x \right) \right) }^{ 2 } } }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } =a\\ y\left( x \right) \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } \frac { \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } -\frac { { y\left( x \right) { \left( \dot { y } \left( x \right) \right) }^{ 2 } } }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } =a\\ \frac { y\left( x \right) \left( 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } \right) }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } -\frac { { y\left( x \right) { \left( \dot { y } \left( x \right) \right) }^{ 2 } } }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } =a\\ \frac { y\left( x \right) +{ y\left( x \right) \left( \dot { y } \left( x \right) \right) }^{ 2 } }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } -\frac { { y\left( x \right) { \left( \dot { y } \left( x \right) \right) }^{ 2 } } }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } =a\\ \frac { y\left( x \right) }{ \sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } } =a\\ y\left( x \right) =a\sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } \\ \frac { y\left( x \right) }{ a } =\sqrt { 1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 } } \\ { \left( \frac { y\left( x \right) }{ a } \right) }^{ 2 }=1+{ \left( \dot { y } \left( x \right) \right) }^{ 2 }\\ { \left( \frac { y\left( x \right) }{ a } \right) }^{ 2 }-{ \left( \dot { y } \left( x \right) \right) }^{ 2 }=1
で、微分方程式を解くような状態になってきました。微分方程式を解くとは平たくいえば、上の方程式を満たす関数 $ y \left(x \right) $ は何か?を考えることなので、関数を推察してみるのはどうでしょうか。
最後の式の形、
\cosh ^{ 2 }{ x } -\sinh ^{ 2 }{ x } =1
の形にとても良く似ています。
そこで、やや天下り的ではありますが、ちょっとしたトリックで、
y\left( x \right) =a\cosh { \left( bx \right) } \\ \dot { y } \left( x \right) =ab\sinh { \left( bx \right) }
とおいてみます。
すると、
{ \left( \frac { a\cosh { \left( bx \right) } }{ a } \right) }^{ 2 }-{ \left( ab\sinh { \left( bx \right) } \right) }^{ 2 }=1\\ { \left( \cosh { \left( bx \right) } \right) }^{ 2 }-{ \left( ab\sinh { \left( bx \right) } \right) }^{ 2 }=1\\ ab\sinh { \left( bx \right) } =\sinh { \left( bx \right) } \\ ab=1\\ b=\frac { 1 }{ a }
したがって、
y\left( x \right) =a\cosh { \left( \frac { x }{ a } \right) }
確かに解を見つけることができました。
ちょっとずるくない?
ふえぇ・・・すみません、ではもうちょっとだけ真面目に解くことを考えてみます。
{ \left( \dot { y } \left( x \right) \right) }^{ 2 }+1={ \left( \frac { y\left( x \right) }{ a } \right) }^{ 2 }\\ { \left( \dot { y } \left( x \right) \right) }^{ 2 }={ \left( \frac { y\left( x \right) }{ a } \right) }^{ 2 }-1\\ \dot { y } \left( x \right) =\pm \sqrt { { \left( \frac { y\left( x \right) }{ a } \right) }^{ 2 }-1 } \\ \pm \frac { \dot { y } \left( x \right) }{ \sqrt { { \left( \frac { y\left( x \right) }{ a } \right) }^{ 2 }-1 } } =1
ここで $ y \left( x \right) = y $ の置換積分の形になっておりますので、
\pm \int { \frac { 1 }{ \sqrt { { \left( \frac { y }{ a } \right) }^{ 2 }-1 } } dy } =x
さらに変数変換を実行して、
\frac { y }{ a } =t\\ \frac { dt }{ dy } =\frac { 1 }{ a } \\ \frac { dy }{ dt } =a\\ dy=adt\\ \pm \int { \frac { a }{ \sqrt { { t }^{ 2 }-1 } } dt } =x\\ \pm \int { \frac { 1 }{ \sqrt { { t }^{ 2 }-1 } } dt } =\frac { x }{ a }
さらにさらに $ t=\cosh { \left( u \right) } $ で置換積分を実行して、
t=\cosh { \left( u \right) } \\ \frac { dt }{ du } =\sinh { \left( u \right) } \\ dt=\sinh { \left( t \right) } du\\ \pm \int { \frac { 1 }{ \sqrt { { \left( \cosh { \left( u \right) } \right) }^{ 2 }-1 } } \sinh { \left( u \right) } du } =\frac { x }{ a } \\ \pm \int { \frac { 1 }{ \sqrt { { \left( \sinh { \left( u \right) } \right) }^{ 2 } } } \sinh { \left( u \right) } du } =\frac { x }{ a } \\ \pm \int { \frac { 1 }{ \sinh { \left( u \right) } } \sinh { \left( u \right) } du } =\frac { x }{ a } \\ \pm \int { 1du } =\frac { x }{ a } \\ \pm u+C=\frac { x }{ a }
ここから変数を元に戻していきますと、
\pm \cosh ^{ -1 }{ \left( t \right) } +C=\frac { x }{ a } \\ \pm \cosh ^{ -1 }{ \left( \frac { y }{ a } \right) } +C=\frac { x }{ a } \\ \pm \cosh ^{ -1 }{ \left( \frac { y }{ a } \right) } =\frac { x }{ a } -C\\ \cosh { \left( \pm \cosh ^{ -1 }{ \left( \frac { y }{ a } \right) } \right) } =\cosh { \left( \frac { x }{ a } -C \right) } \\ \frac { y }{ a } =\cosh { \left( \frac { x }{ a } -C \right) } \\ y=a\cosh { \left( \frac { x }{ a } -C \right) } \\ y=a\cosh { \left( \frac { x-aC }{ a } \right) } \\ y=a\cosh { \left( \frac { x+S }{ a } \right) } \\ y\left( x \right) =a\cosh { \left( \frac { x+S }{ a } \right) }
大変長くなってしまいましたが、$ S $ は平行移動ですので、たしかに解にたどり着くことができました。
これでめでたしめでたし、ではなく折り返し地点です。ここからは得られた式をベースにコンピュータで遊んでみましょう!
パラメータ化
一つの応用として、コンピュータ上で懸垂線を自由に描画できたら、きっと楽しいことでしょう!
確かに自由なパラメータ $a$ を使っていろんな懸垂線を描画してみることは簡単です。ただ自然と湧いてくる欲求としては、現実世界のように、2点と、その長さを使って描画したい場合、どのように扱えばよいでしょうか?
これを整理すると、
\left( X_{ 1 },Y_{ 1 } \right) ,\left( X_{ 2 },Y_{ 2 } \right)
の2点を通り、そして $ X_{ 1 }~ X_{ 2 } $ の間の長さが $ s $ の場合に、
先の一般懸垂線を平行移動した式
y\left( x \right) =a\cosh { \left( \frac { x+S }{ a } \right) } +T
のパラメータ、$ a, S, T $ を算出するというようにしてはどうでしょうか?
aを求める
いきなり全部一気に考えるのは大変です。なので一番大変そうな $a$から考えてみます。
ただ$a$を考える時、先の $S,T$ については、式の平行移動のみのため、
y\left( x \right) =a\cosh { \left( \frac { x }{ a } \right) }
この状態で $ a $ を先に算出してみます。
平行移動を無視するために、ちょっとしたトリックで2点の水平距離と垂直距離を考えます。
水平距離を $h$ , 垂直距離を $v$ とおきます。この量は方程式を平行移動しても変化しない量というのがポイントです。
平行移動を無視した世界でみた2点を仮に、
\left( x_{ 1 },y_{ 1 } \right) ,\left( x_{ 2 },y_{ 2 } \right)
とすれば、まず $ v $ については、
v=a\cosh { \left( \frac { x_{ 2 } }{ a } \right) } -a\cosh { \left( \frac { x_{ 1 } }{ a } \right) }
となります。※後に使うのが $ v^2 $ の量であるため、負の値は気にしないことにします。
次に、パラメータとして与えること前提ではありますが、いったん $ s $ を考えます。
s=\int _{ x_{ 1 } }^{ x_{ 2 } }{ \sqrt { 1+{ \left( \frac { d }{ dx } y\left( x \right) \right) }^{ 2 } } dx } \\ y\left( x \right) =a\cosh { \left( \frac { x }{ a } \right) } \\ \frac { d }{ dx } y\left( x \right) =a\sinh { \left( \frac { x }{ a } \right) } \frac { 1 }{ a } =\sinh { \left( \frac { x }{ a } \right) } \\ \int _{ x_{ 1 } }^{ x_{ 2 } }{ \sqrt { 1+{ \left( \frac { d }{ dx } y\left( x \right) \right) }^{ 2 } } dx } \\ =\int _{ x_{ 1 } }^{ x_{ 2 } }{ \sqrt { 1+{ \left( \sinh { \left( \frac { x }{ a } \right) } \right) }^{ 2 } } dx } \\ =\int _{ x_{ 1 } }^{ x_{ 2 } }{ \cosh { \left( \frac { x }{ a } \right) } dx } \\ \frac { x }{ a } =t\\ \frac { dt }{ dx } =\frac { 1 }{ a } \\ \frac { dx }{ dt } =a\\ dx=adt\\ =\int _{ \frac { x_{ 1 } }{ a } }^{ \frac { x_{ 2 } }{ a } }{ a\cosh { \left( t \right) } dt } \\ =\left[ a\sinh { \left( t \right) } \right] ^{ \frac { x_{ 2 } }{ a } }_{ \frac { x_{ 1 } }{ a } }\\ s=a\sinh { \left( \frac { x_{ 2 } }{ a } \right) } -a\sinh { \left( \frac { x_{ 1 } }{ a } \right) } \\
最後に $ { s }^{ 2 }-{ v }^{ 2 } $ という量を考えます
はじめに積和の公式を適用しておくと、式の展開が楽になります。
\\ \sinh { \left( A \right) } -\sinh { \left( B \right) } =2\sinh { \left( \frac { A+B }{ 2 } \right) } \cosh { \left( \frac { A-B }{ 2 } \right) } \\ \cosh { \left( A \right) } -\cosh { \left( B \right) } =2\sinh { \left( \frac { A+B }{ 2 } \right) } \sinh { \left( \frac { A-B }{ 2 } \right) }
これを使って、$ { s }^{ 2 }-{ v }^{ 2 } $ を計算してみると、
s=a\sinh { \left( \frac { x_{ 2 } }{ a } \right) } -a\sinh { \left( \frac { x_{ 1 } }{ a } \right) } \\ =a\left( \sinh { \left( \frac { x_{ 2 } }{ a } \right) } -\sinh { \left( \frac { x_{ 1 } }{ a } \right) } \right) \\ =a2\cosh { \left( \frac { x_{ 2 }+x_{ 1 } }{ 2a } \right) } \sinh { \left( \frac { x_{ 2 }-x_{ 1 } }{ 2a } \right) } \\ v=a\cosh { \left( \frac { x_{ 2 } }{ a } \right) } -a\cosh { \left( \frac { x_{ 1 } }{ a } \right) } \\ =a\left( \cosh { \left( \frac { x_{ 2 } }{ a } \right) } -\cosh { \left( \frac { x_{ 1 } }{ a } \right) } \right) \\ =a2\sinh { \left( \frac { x_{ 2 }+x_{ 1 } }{ 2a } \right) } \sinh { \left( \frac { x_{ 2 }-x_{ 1 } }{ 2a } \right) } \\ { s }^{ 2 }-{ v }^{ 2 }={ a }^{ 2 }4{ \cosh ^{ 2 }{ \left( \frac { x_{ 2 }+x_{ 1 } }{ 2a } \right) } }\sinh ^{ 2 }{ \left( \frac { x_{ 2 }-x_{ 1 } }{ 2a } \right) } -{ a }^{ 2 }4\sinh ^{ 2 }{ \left( \frac { x_{ 2 }+x_{ 1 } }{ 2a } \right) } \sinh ^{ 2 }{ \left( \frac { x_{ 2 }-x_{ 1 } }{ 2a } \right) } \\ ={ a }^{ 2 }4\sinh ^{ 2 }{ \left( \frac { x_{ 2 }-x_{ 1 } }{ 2a } \right) } \left\{ \cosh ^{ 2 }{ \left( \frac { x_{ 2 }+x_{ 1 } }{ 2a } \right) } -{ \sinh ^{ 2 }{ \left( \frac { x_{ 2 }+x_{ 1 } }{ 2a } \right) } } \right\} \\ ={ a }^{ 2 }4\sinh ^{ 2 }{ \left( \frac { x_{ 2 }-x_{ 1 } }{ 2a } \right) } \\ { s }^{ 2 }-{ v }^{ 2 }={ a }^{ 2 }4\sinh ^{ 2 }{ \left( \frac { h }{ 2a } \right) } \\ \sqrt { { s }^{ 2 }-{ v }^{ 2 } } =a2\sinh { \left( \frac { h }{ a2 } \right) } \\ a2\sinh { \left( \frac { h }{ a2 } \right) } -\sqrt { { s }^{ 2 }-{ v }^{ 2 } } =0
なんと未知の $a$ だけの方程式が導かれました。あとはこの $a$ を求めるわけですが、残念ながらこれは解析的な解がなく、数値的な解法が必要のようです。
数値解法
最後の方程式は $a$ が正のときには単調減少のため、正のときだけを考える今回のケースでは素直な解き方でも局所解に陥る心配はなさそうです。ただニュートン法を適用する際に、初期値にはかなり近い値を選びたいところです。そこで元の方程式のテイラー展開の逆関数を使うことにします。
今回はこのあたりはwolframalphaに投げてしまうと、
f\left( a \right) =2a\sinh \left( \frac { h }{ 2a } \right) +T\\ f\left( a \right) =T+h+\frac { h^{ 3 } }{ 24a^{ 2 } } +\frac { h^{ 5 } }{ 1920a^{ 4 } } +...
https://www.wolframalpha.com/input/?i=taylor+series+2a*sinh(h%2F(2a))+%2B+T
これはdesmosで確認するとなかなか良い近似になっています。
これの逆関数は、
f^{ -1 }\left( x \right) =\frac { \sqrt { -\frac { \sqrt { 5 } \sqrt { -h^{ 5 }\left( h+6T-6x \right) +5h^{ 3 } } }{ h+T-x } } }{ 4\sqrt { 15 } }
となります。desmosで見てみると、
確かにいい感じです。
ニュートン法の漸化式は、
x_{ n+1 }=x_{ n }-\frac { f\left( x_{ n } \right) }{ f^{ ' }\left( x_{ n } \right) }
であり、fの微分は、
\frac { d }{ da } \left( 2a\sinh \left( \frac { h }{ 2a } \right) +T \right) =2\sinh \left( \frac { h }{ 2a } \right) -\frac { h\cosh \left( \frac { h }{ 2a } \right) }{ a }
以上でもって、ニュートン法の実装は以下のようになります。
template <int n>
static double Pow(double v) {
static_assert(n > 0, "Power can’t be negative");
double n2 = Pow<n / 2>(v);
return n2 * n2 * Pow<n & 1>(v);
}
template <> double Pow<1>(double v) { return v; }
template <> double Pow<0>(double v) { return 1.0; }
// important
// h: holizontal distance
// v: vertical distance
// T = - Sqrt(s^2 - v^2)
// f(a) = 2*a*sinh(h/(a2)) + T
// for finding a, f(a) == 0
inline double f(double a, double h, double sqrt_s2_minus_v2) {
double T = -sqrt_s2_minus_v2;
return 2.0 * a * std::sinh(h / (a * 2.0)) + T;
}
// f'(a)
// D[2*a*sinh(h/(2a)) + T, a]
inline double dfdx(double a, double h) {
return 2.0 * std::sinh(h / (2.0 * a)) - (h * std::cosh(h / (2.0 * a)) / a);
}
// f(a) = y
// f^(-1)(y) = a
inline double f_inverse_taylor(double y, double h, double sqrt_s2_minus_v2) {
double T = -sqrt_s2_minus_v2;
// constant
static const double k_one_over_4_sqrt_15 = 1.0 / (4.0 * std::sqrt(15.0));
static const double k_sqrt_5 = std::sqrt(5.0);
// Solve[T+h + h^3/(24 a^2) + h^5/(1920 a^4)==x, a]
// CForm(sqrt(-(sqrt(5) sqrt(-h^5 (h + 6 T - 6 x)) + 5 h^3)/(h + T - x))/(4 sqrt(15)))
return std::sqrt(-(k_sqrt_5 * std::sqrt(-(Pow<5>(h) * (h + 6.0 * T - 6.0 * y))) + 5 * Pow<3>(h)) / (h + T - y)) * k_one_over_4_sqrt_15;
}
// find a, f(a) = y
// f^(-1)(y) = a
inline double f_inverse_newton(double y, double h, double sqrt_s2_minus_v2, int *iteratedCount = nullptr) {
double T = -sqrt_s2_minus_v2;
double eps = 1.0e-9;
double x_cur = f_inverse_taylor(y, h, sqrt_s2_minus_v2);
double f_value = f(x_cur, h, sqrt_s2_minus_v2) - y;
if (iteratedCount) {
*iteratedCount = 1;
}
for (int i = 0; i < 100; ++i) {
if (std::isfinite(x_cur) == false) {
break;
}
if (std::fabs(f_value) < eps) {
break;
}
double move = -f_value / dfdx(x_cur, h);
x_cur = x_cur + move;
f_value = f(x_cur, h, sqrt_s2_minus_v2) - y;
if (iteratedCount) {
(*iteratedCount)++;
}
}
return x_cur;
}
inline double solve_a(double h, double v, double s) {
return f_inverse_newton(0.0, h, sqrt(s * s - v * v));
}
S, T を求める
$ a $ が求まったので、あとは平行移動を片付けてしまいます。
y\left( x \right) =a\cosh { \left( \frac { x+S }{ a } \right) } +T
二点の座標と、線の長さを指定する、と述べましたが、1点目が $ \left( 0,0 \right) $ の座標に固定しておくと、利便性を損なわずに数式を簡単にすることができます。
そこで2点を、
\left( 0,0 \right) ,\left( X,Y \right)
とすることにして、
x=0,y\left( 0 \right) =0\\ 0=a\cosh { \left( \frac { S }{ a } \right) } +T\\ T=-a\cosh { \left( \frac { S }{ a } \right) } \\ y\left( x \right) =a\cosh { \left( \frac { x+S }{ a } \right) } -a\cosh { \left( \frac { S }{ a } \right) } \\ \\ x=X,y\left( X \right) =Y\\ Y=a\cosh { \left( \frac { X+S }{ a } \right) } -a\cosh { \left( \frac { S }{ a } \right) }
あとはSについて解きます。
\frac { Y }{ a } =\cosh { \left( \frac { X+S }{ a } \right) } -\cosh { \left( \frac { S }{ a } \right) }
に積和の公式を使って、
\frac { Y }{ a } =2\sinh { \left( \frac { X+S }{ 2a } +\frac { S }{ 2a } \right) } \sinh { \left( \frac { X+S }{ 2a } -\frac { S }{ 2a } \right) } \\ \frac { Y }{ a } =2\sinh { \left( \frac { X+2S }{ 2a } \right) } \sinh { \left( \frac { X }{ 2a } \right) } \\ \frac { Y }{ a2\sinh { \left( \frac { X }{ 2a } \right) } } =\sinh { \left( \frac { X+2S }{ 2a } \right) } \\ \frac { X+2S }{ 2a } =\sinh ^{ -1 }{ \left( \frac { Y }{ a2\sinh { \left( \frac { X }{ 2a } \right) } } \right) } \\ X+2S=2a\sinh ^{ -1 }{ \left( \frac { Y }{ a2\sinh { \left( \frac { X }{ 2a } \right) } } \right) } \\ 2S=2a\sinh ^{ -1 }{ \left( \frac { Y }{ a2\sinh { \left( \frac { X }{ 2a } \right) } } \right) } -X\\ S=a\sinh ^{ -1 }{ \left( \frac { Y }{ a2\sinh { \left( \frac { X }{ 2a } \right) } } \right) } -\frac { X }{ 2 }
※ $\sinh\left(x\right)$ は単調増加であり、全単射なので思考停止で逆関数を使えます
これで $ S, T $ 共に求まりました。
あとはコード化すると、
struct Curve {
double a = 1.0;
double S = 0.0;
double T = 0.0;
double evaluate(double x) const {
return a * std::cosh((x + S) / a) + T;
}
};
/*
(x1, x2) = (0, 0)
(x2, y2) = (X, Y)
length: s Catenary curve
*/
inline Curve curve(double X, double Y, double s) {
Curve c;
c.a = solve_a(X, std::fabs(Y), s);
c.S = c.a * std::asinh(Y / (c.a * 2.0 * std::sinh(X / (2.0 * c.a)))) - X * 0.5;
c.T = -c.a * std::cosh(c.S / c.a);
return c;
}
描画
以上をopenframeworksで描画してみます。楽しい!✌('ω'✌ )三✌('ω')✌三( ✌'ω')✌
※本コードでは、直線距離よりも $ s $ が短いケースは今回は気にしないことにします(そもそも矛盾していますし、その場合は描画しないか、直線になるかといった形になってしまうため)
紐の長さについて等間隔でオブジェクトを配置する
もうちょっと遊んでみましょう。ある線の長さの場所のx座標を調べるにはどうしたらいいでしょうか?最終的な方程式は、
y\left( x \right) =a\cosh { \left( \frac { x+S }{ a } \right) +T }
でしたので、求めたいx座標を $ X_{ i } $ とすると、
\frac { d }{ dx } y\left( x \right) =a\sinh { \left( \frac { x+S }{ a } \right) } \frac { 1 }{ a } =\sinh { \left( \frac { x+S }{ a } \right) } \\ s=\int _{ 0 }^{ X_{ i } }{ \sqrt { 1+{ \left( \frac { d }{ dx } y\left( x \right) \right) }^{ 2 } } dx } \\ =\int _{ 0 }^{ X_{ i } }{ \sqrt { 1+{ \left( \sinh { \left( \frac { x+S }{ a } \right) } \right) }^{ 2 } } dx } \\ =\int _{ 0 }^{ X_{ i } }{ \cosh { \left( \frac { x+S }{ a } \right) } dx }
と $ s $ が表せますので、置換積分しつつ $ X_{ i } $ について解くと、
\frac { x+S }{ a } =t\\ \frac { dt }{ dx } =\frac { 1 }{ a } \\ \frac { dx }{ dt } =a\\ dx=adt\\ =\int _{ \frac { 0+S }{ a } }^{ \frac { X_{ i }+S }{ a } }{ a\cosh { \left( t \right) } dt } \\ =\int _{ \frac { S }{ a } }^{ \frac { X_{ i }+S }{ a } }{ a\cosh { \left( t \right) } dt } \\ =\left[ a\sinh { \left( t \right) } \right] ^{ \frac { X_{ i }+S }{ a } }_{ \frac { S }{ a } }\\ s=a\sinh { \left( \frac { X_{ i }+S }{ a } \right) } -a\sinh { \left( \frac { S }{ a } \right) } \\ \frac { s }{ a } =\sinh { \left( \frac { X_{ i }+S }{ a } \right) } -\sinh { \left( \frac { S }{ a } \right) } \\ \frac { s }{ a } +\sinh { \left( \frac { S }{ a } \right) } =\sinh { \left( \frac { X_{ i }+S }{ a } \right) } \\ \\ \sinh ^{ -1 }{ \left( \frac { s }{ a } +\sinh { \left( \frac { S }{ a } \right) } \right) } =\frac { X_{ i }+S }{ a } \\ X_{ i }=a\sinh ^{ -1 }{ \left( \frac { s }{ a } +\sinh { \left( \frac { S }{ a } \right) } \right) } -S
スパッと求まりました!
したがって実装は、
struct Curve {
double a = 1.0;
double S = 0.0;
double T = 0.0;
double evaluate(double x) const {
return a * std::cosh((x + S) / a) + T;
}
double x_for_s(double s) {
return a * std::asinh(s / a + std::sinh(S / a)) - S;
}
};
となります。
これを使って描画してみると、
いい感じです。これでクリスマスの飾り付けは心配ありませんね!
テスト
しかし悲しいかなプログラムにはバグがつきものであり、簡単にでもテストを記述しておくと多少なりとも心の平穏につながるでしょう。
上記の仕組みをつかって生成した任意の懸垂線は、
- 数値積分によって測った長さが $s$ になっていること
- $ \left( 0,0 \right) ,\left( X,Y \right) $ を通過していること
- ある長さ $s$ から $X_i$ を逆算したとき、0~$X_i$の長さが $s$ になっていること
を満たしている必要があるでしょう。
したがって、試しにいっぱい懸垂線を作ってみて、これらの条件を満たしているかをテストする、というアイディアはどうでしょうか?
おんなじ量を、違うアプローチで計算しても、結果は同じであるべきだ、という考え方です。
数値積分は、実装が楽で精度もそこそこ良い合成シンプソン公式を使います。
積分範囲 [a, b] を均等に $n$ (偶数個)に分割したとき、積分は以下のように近似できます
h=\frac { b-a }{ n } \\ x_{ i }=a+hi\\ \int _{ a }^{ b }{ f\left( x \right) dx } \simeq \frac { h }{ 3 } \left[ f\left( x_{ 0 } \right) +4f\left( x_{ 1 } \right) +2f\left( x_{ 2 } \right) +4f\left( x_{ 3 } \right) +...+4f\left( x_{ n-1 } \right) +f\left( x_{ n } \right) \right]
素直にコードにすると以下のようになります。
inline double integrate_composite_simpson(std::function<double(double)> f, double a, double b, int n) {
assert((n & 0x1) == 0);
double sum = 0;
double h = (b - a) / n;
for (int i = 1; i < n; ++i) {
double c = (i & 0x1) ? 4.0 : 2.0;
double x_i = a + h * i;
sum += c * f(x_i);
}
sum += f(a) + f(b);
return sum * h / 3.0;
}
おっと、懸垂線の微分も必要だったので、そちらも準備します。
\frac { d }{ dx } \left( a\cosh { \left( \frac { x+S }{ a } \right) } +T \right) =a\cosh { \left( \frac { x+S }{ a } \right) } \frac { 1 }{ a } =\sinh { \left( \frac { x+S }{ a } \right) }
実装は、以下のようになります。
struct Curve {
double a = 1.0;
double S = 0.0;
double T = 0.0;
double evaluate(double x) const {
return a * std::cosh((x + S) / a) + T;
}
double evaluate_dfdx(double x) const {
return std::sinh((x + S) / a);
}
double x_for_s(double s) {
return a * std::asinh(s / a + std::sinh(S / a)) - S;
}
};
これらを使って、ランダムに点を生成して条件を満たすかを確認します。
void test() {
std::mt19937 engine;
std::uniform_real_distribution<> random_x(0.01, 1000.0);
std::uniform_real_distribution<> random_y(-1000.0, 1000.0);
double eps = 0.001;
for (int i = 0; i < 100000; ++i) {
double x = random_x(engine);
double y = random_y(engine);
double min_s = std::sqrt(x * x + y * y);
std::uniform_real_distribution<> random_s(min_s + eps, min_s + eps + 1000.0);
double s = random_s(engine);
catenary::Curve curve = catenary::curve(x, y, s);
double numeric_s = integrate_composite_simpson([curve](double x) {
double dfdx = curve.evaluate_dfdx(x);
return std::sqrt(1.0 + dfdx * dfdx);
}, 0, x, 1000);
if (std::fabs(curve.evaluate(0)) > 0.000001) {
abort();
}
if (std::fabs(curve.evaluate(x) - y) > 0.000001) {
abort();
}
if (std::fabs(s - numeric_s) > eps) {
abort();
}
std::uniform_real_distribution<> random_at_s(0.0, s);
double at_s = random_at_s(engine);
double at_x = curve.x_for_s(at_s);
double numeric_at_s = integrate_composite_simpson([curve](double x) {
double dfdx = curve.evaluate_dfdx(x);
return std::sqrt(1.0 + dfdx * dfdx);
}, 0, at_x, 1000);
if (std::fabs(at_s - numeric_at_s) > eps) {
abort();
}
}
}
テストケースを乱数で生成する方法は、案外いろんなところで使えて便利ではないでしょうか。
ソースコード
ここまでのフルソースはgithubからアクセス可能です。
https://github.com/Ushio/Catenaly
ビルドするにはopenframeworks が必要です。記事製作時に使ったバージョンは、0.9.8になります。
http://openframeworks.cc/ja/
まとめ
懸垂線程度で大げさな数学が多かった気がしますが、変分法なんかはそれ自体はなかなかとっつきづりらい分野だったりするので、練習としての題材としては悪くないのではないでしょうか?ちなみに私は何度も式変形に失敗してすぐ解けなくなるのを何十回もやりました。トホホ。
また環境にほとんど依存せず、どこへでも移植できるので、しっかりまとめておくと活用できる場面はあるかもしれません。
参考資料
"Wikipedia Catenary"
https://en.wikipedia.org/wiki/Catenary#Determining_parameters
"工科系のための 解析力学"
https://www.shokabo.co.jp/mybooks/ISBN978-4-7853-2240-3.htm
"物理数学の直観的方法"
http://bookclub.kodansha.co.jp/product?isbn=9784062577380
"高校数学の美しい物語 懸垂線の2通りの導出"
https://mathtrain.jp/catenary
"懸垂線に関する質問について", 新潟工科大学 情報電子工学科 竹野茂治
http://takeno.iee.niit.ac.jp/~shige/math/lecture/misc/data/hyper2.pdf
"Catenary Curve"
https://conversationofmomentum.wordpress.com/2014/08/10/catenary-curve/
"最速降下曲線の導き方"
http://s1nakagiri.blogspot.jp/2017/07/blog-post_80.html
"物理のかぎしっぽ 変分法2"
http://hooktail.sub.jp/mathInPhys/variations2/