最小二乗法の基礎を丁寧に

最小二乗法？

最小二乗法は、複雑なデータをなにがしかの関数の組み合わせで近似する手法です。
これならわかる応用数学教室を参考にしながら、

大変シンプルに、

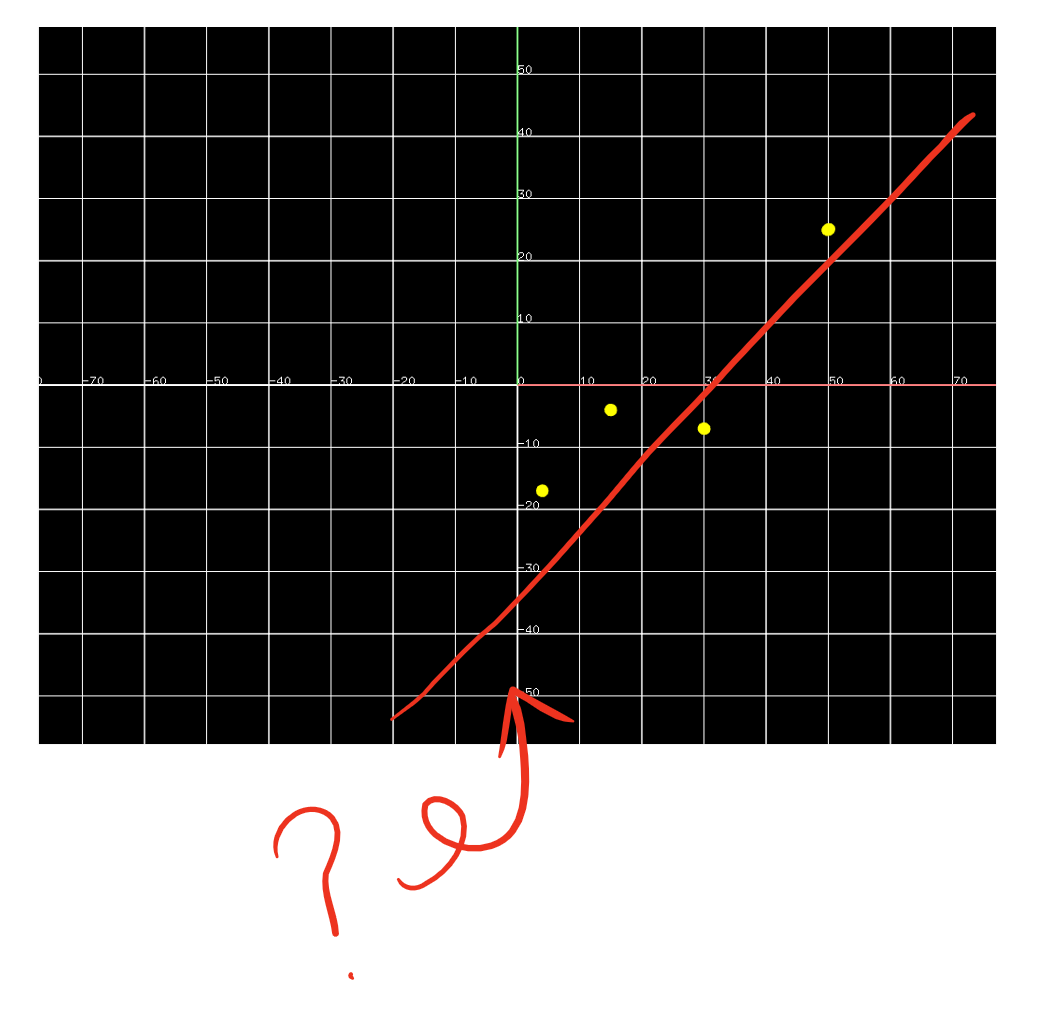
数値(x, y)、具体的には

(4, -17)
(15, -4)
(30, -7)
(50, 25)

のいくつかのデータを直線

f(x) = ax + b

で近似することを目標にします。
図にするとこんな感じです

大変シンプルですが、シグマ、偏微分、連立方程式、行列などの要素が登場します。
計算器と数学のコラボレーションとしてもとても面白いです。
なるべく平易に、カジュアルにまとめてみます。

プログラミング環境

環境は、openframeworksを使います。
カジュアルなビジュアライズが可能ですし、win, osxどちらでも可能です。

基本戦略

根幹にある考えは、誤差を最小にするというものです。

では誤差はどう考えたらいいでしょうか？
それぞれのxについて、そのときのyの値と、近似関数による答えyの距離の二乗を求めて足し合わせるなんてどうでしょうか？
例えば以下のように

	std::vector<ofVec2f> plots = {
		{ 4, -17 },
		{ 15, -4 },
		{ 30, -7 },
		{ 50, 25 },
	};
	float error = 0.0f;
	float a = 0.8f;
	float b = -21.0f;
	for (int i = 0; i < plots.size(); ++i) {
		float x = plots[i].x;
		float y = plots[i].y;

		float truthValue = y;
		float maybe = a * x + b;

		error += std::pow(truthValue - maybe, 2.0f);
	}
	printf("%f", error);

とすると誤差が計算できます。
式として表現してみましょう。

J = \sum_{i=1}^{N} (y_i - (ax_i + b))^2

どうやらこのJを最小化すればよさそうです。

また、
後々の計算で楽になるために、２分の１しておくと良いと本の中で触れられています。
半分にしたところで最小化になんら影響はありません。

J = \frac{1}{2} \sum_{i=1}^{N} (y_i - (ax_i + b))^2

最小化する

極大極小の考え方でいうと、
a, bそれぞれに対して、微分して0になるところが最小点になります。
それぞれ行うので偏微分です。
偏微分は、一つの変数に着目していったんほかの変数を定数と扱って微分する手法です。

まずはaについての偏微分です。
シグマが入っていますが、これは気にせずそのまま微分できます。
おっと、べき乗があります。これは好都合、微分の展開が楽です。さきほど誤差を、距離の二乗の和としたからですね。
合成関数の微分を行いましょう。
合成関数の片方は、

f(x) = x^2\\
f'(x) = 2x

もう片方は

g(a) = y_i - ax_i - b\\
g'(a) = -x_i

となるので、

\frac{\partial J}{\partial a} = \frac{1}{2} \sum_{i=1}^{N} 2(y_i - ax_i - b)(-x_i)\\
= \sum_{i=1}^{N} (y_i - ax_i - b)(-x_i)\\
= \sum_{i=1}^{N} (ax_i^2 + bx_i - x_iy_i)\\
= \sum_{i=1}^{N} ax_i^2 + \sum_{i=1}^{N}bx_i - \sum_{i=1}^{N}x_iy_i\\
= a\sum_{i=1}^{N} x_i^2 + b\sum_{i=1}^{N}x_i - \sum_{i=1}^{N}x_iy_i\\

とここまで持ってこれます。ここで2分の1があるおかげですっきりしました。
yも同様の流れでやれば、

\frac{\partial J}{\partial b} = \frac{1}{2} \sum_{i=1}^{N} 2(y_i - ax_i - b)(-1)\\
= \sum_{i=1}^{N} (y_i - ax_i - b)(-1)\\
= \sum_{i=1}^{N} (ax_i + b - y_i)\\
= \sum_{i=1}^{N} ax_i + \sum_{i=1}^{N}b - \sum_{i=1}^{N}y_i\\
= a\sum_{i=1}^{N} x_i + b\sum_{i=1}^{N}1 - \sum_{i=1}^{N}y_i\\

ともってこれます。
これら２つが０になるので、連立方程式ができます。

\begin{eqnarray}
  {}
  a\sum_{i=1}^{N} x_i^2 + b\sum_{i=1}^{N}x_i = \sum_{i=1}^{N}x_iy_i & \\
  a\sum_{i=1}^{N} x_i + b\sum_{i=1}^{N}1 = \sum_{i=1}^{N}y_i &
\end{eqnarray}

連立方程式を解く

ここでは行列でまず表現します。

\left(
    \begin{array}{cc}
      \sum_{i=1}^{N} x_i^2 & \sum_{i=1}^{N}x_i\\
      \sum_{i=1}^{N} x_i & \sum_{i=1}^{N}1 
    \end{array}
\right)
\left(
    \begin{array}{c}
      a \\
      b 
    \end{array}
\right)
=
\left(
    \begin{array}{c}
      \sum_{i=1}^{N}x_iy_i \\
      \sum_{i=1}^{N}y_i
    \end{array}
\right)

a, bを求めたいわけですから、あとは逆行列を求めればすぐです。

\left(
    \begin{array}{c}
      a \\
      b 
    \end{array}
\right)
=
\left(
    \begin{array}{cc}
      \sum_{i=1}^{N} x_i^2 & \sum_{i=1}^{N}x_i\\
      \sum_{i=1}^{N} x_i & \sum_{i=1}^{N}1 
    \end{array}
\right)^{-1}
\left(
    \begin{array}{c}
      \sum_{i=1}^{N}x_iy_i \\
      \sum_{i=1}^{N}y_i
    \end{array}
\right)

ここまできたらプログラムまで落とし込んでしまいましょう。
行列演算はなんでもいいのですが、今回は自分が好きなglmを使います。（ofに2x2行列クラスが無いのはあまり褒められたものではないですね・・・まあ2x2の逆行列くらいは大したことないのですが）

素直に行列に要素を突っ込んで、素直に解を求めます。（解がないのは今回は考慮していません）

#pragma once

#include "ofMain.h"

class ofApp : public ofBaseApp {
public:
	void setup();
	void update();
	void draw();

	void keyPressed(int key);
	void keyReleased(int key);
	void mouseMoved(int x, int y);
	void mouseDragged(int x, int y, int button);
	void mousePressed(int x, int y, int button);
	void mouseReleased(int x, int y, int button);
	void mouseEntered(int x, int y);
	void mouseExited(int x, int y);
	void windowResized(int w, int h);
	void dragEvent(ofDragInfo dragInfo);
	void gotMessage(ofMessage msg);

	ofEasyCam _camera;
	std::vector<ofVec2f> _plots;
};

#include "ofApp.h"

#include <glm/glm.hpp>

//--------------------------------------------------------------
void ofApp::setup(){
	_plots.emplace_back(4, -17);
	_plots.emplace_back(15, -4);
	_plots.emplace_back(30, -7);
	_plots.emplace_back(50, 25);

	_camera.setDistance(100);
}

//--------------------------------------------------------------
void ofApp::draw(){
	// 最小二乗法
	float m0 = 0.0f;
	float m1 = 0.0f;
	float m2 = 0.0f;
	float m3 = 0.0f;

	float v0 = 0.0f;
	float v1 = 0.0f;
	
	for (int i = 0; i < _plots.size(); ++i) {
		ofVec2f p = _plots[i];
		float x = p.x;
		float y = p.y;

		m0 += x * x;
		m1 += x;
		m2 += x;
		m3 += 1.0f;

		v0 += x * y;
		v1 += y;
	}
	glm::mat2 m(glm::vec2(m0, m1), glm::vec2(m2, m3));
	glm::vec2 v(v0, v1);

	glm::vec2 ab = glm::inverse(m) * v; /* 連立方程式を解く */

	ofSetColor(255);
	ofClear(0);

	_camera.begin();
	ofPushMatrix();
	ofRotateY(90);
	ofDrawGridPlane(10, 10, true);
	ofPopMatrix();

	ofDrawAxis(100);

	ofSetColor(255, 255, 0);
	for (auto p : _plots) {
		ofDrawSphere(p, 1.0f);
	}
	
	ofSetColor(255, 0, 255);
	ofVec2f p0(-100.0f, ab.x * -100.0f + ab.y);
	ofVec2f p1( 100.0f, ab.x *  100.0f + ab.y);
	ofDrawLine(p0, p1);

	_camera.end();
}

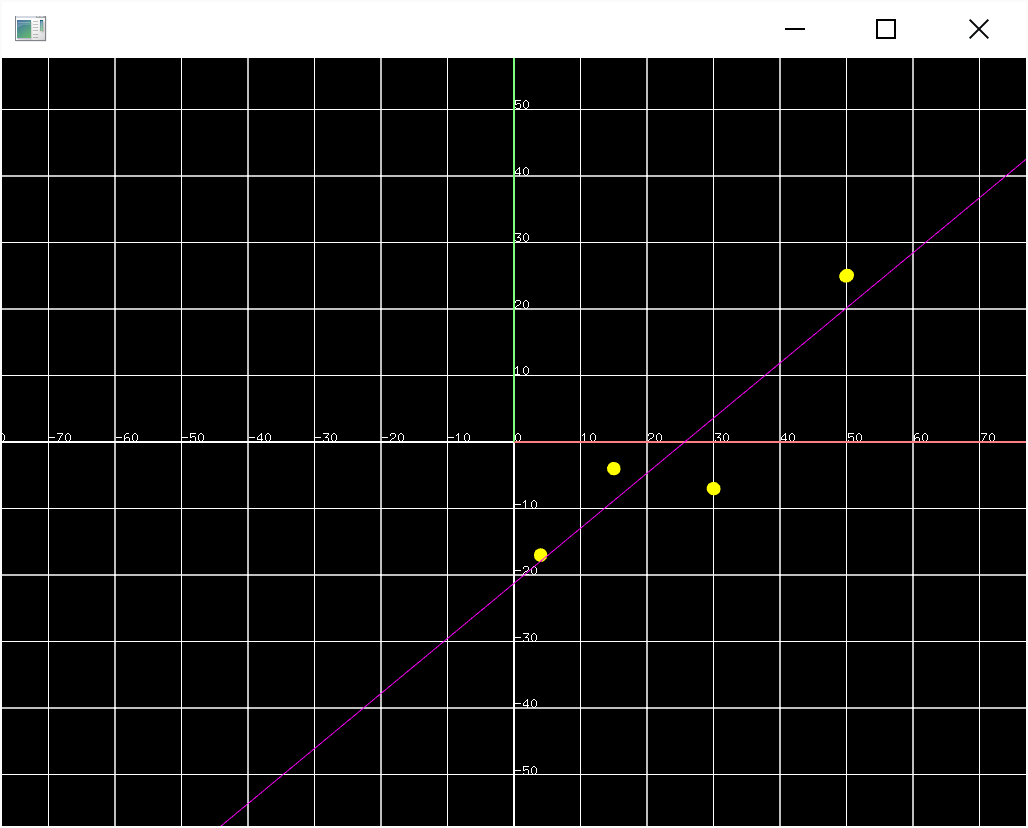
おめでとうございます！
実行すると見事に近似直線が描画されます。

まとめ

最小二乗法は数学と計算機との密接なコラボレーションによって、大変大きな力になってくれるテクニックです。
今回は本当に基礎の基礎でしたが、とても実りのある技術です。
もしまだあまり着手したことがないなら、
ぜひ自分の手で触れてみてはいかがでしょうか。きっと新しい発見があるはずです。