確率密度関数からモンテカルロ積分まで

皆さんこんにちは、レイ、飛ばしてますでしょうか？
これはレイトレ Advent Calender 2016 11日目の記事です。

自分はいったん飛ばすのを休憩して、今更高校のときすっ飛ばした数Ⅲを、

坂田アキラの 数IIIの微分積分が面白いほどわかる本

にて勉強したりしてました。
とても気持ちのいい問題が多く、サクサク進むことができました。おすすめです。

ゴール

さて、本題ですが、確率的な考え方はレイトレにおいてとても大事です。Veach氏の論文においても、最初の方から登場します。PBRT v3では748ページが該当箇所でしょうか。しかしこの本、圧倒的ボリュームですね。。。
今回は確率の数学を積分の問題へ適用するところを、直観的理解を目指してまとめていきたいと思います。
なので数式はなるべく省略しないよう、心がけたいと思います。

確率密度関数（probability density function）

まずは確率密度関数とはまずなんぞ？という話です。

とあるXがランダムな数値、たとえば0.1とか0.5とか、1000.0とか、なにか連続的な数値をとるとき、
とあるXが、　　xと、δxだけちょっと離れた場所の間に存在する確率を、

P\left( x\le X<x+\delta x \right) 

と表記します。そしてそれが、

P\left( x\le X<x+\delta x \right) = f\left( x \right) \delta x

を満たすf(x)を確率密度関数と呼びます。
でもこれだけだとあまりピンと来ないです。なので図にして考えてみましょう。

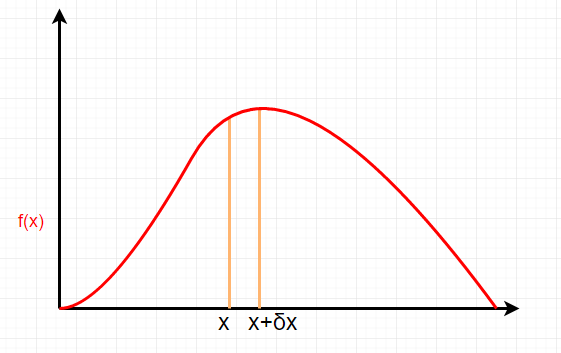
例えばXはなんらかの理由により、出現確率が偏っていて、あるf(x)が以下のような形になっていたとします。

この時、

f\left( x \right) \delta x

って何か？と考えたとき、このオレンジとf(x)とx軸で囲われた部分の面積である、と解釈して良さそうです。
ということは、f(x)はXの確率密度関数であるならば、
f(x)をaからbで定積分した値が、Xがaとbの間にある確率を示す、とも言えます。
これを数式にしてみると、

P\left( a\le X\le b \right) =\int _{ a }^{ b }{ f\left( x \right) dx } 

となります。
実際に定積分してみると、Xがaとbの間にある確率として、例えば0.2なり、0.3なり適切な数字が返ってきます。
ちなみにf(x)の全域について積分は1になります。
これはXが全域のどこかにいる確率は、やはり100%だからです。

\int _{ -\infty  }^{ \infty  }{ f\left( x \right) dx } =1

ちなみにprobability density functionなので、pdfと略されたりもします。

累積分布関数(cumulative distribution function)

さて、確率密度関数はわかってきました。
次に、Xが、ある値x以下である確率を考えてみます。
さっきの確率密度関数の話から、積分によって表現できそうです。

P\left( X<x \right) = \int _{ -\infty  }^{ x }{ f\left( t \right) dt } 

もしXが負の値を取らないなら、

P\left(X<x \right) = \int _{ 0 }^{ x }{ f\left( t \right) dt } 

と表現したって差し支えないでしょう。
これにF(x)と名前をつけてみます。

P\left( X<x \right) = \int _{ -\infty  }^{ x }{ f\left( t \right) dt } = F(x)

このF(x)を累積分布関数（cumulative distribution function, CDF)と呼びます。
なんでこんな関数を考えるのか？は後で触れます。

ある確率密度関数を持つ確率変数Xの作り方

ここまで理解すると、だんだんとXの具体的な姿を考えたくなってきます。
具体的な姿がわかれば、計算機を使ってXを垣間見ることができそうです。
さて、Xを実装するにあたって、色々手法があるようですが、今回は有名な逆関数法について考えます。

まず最初に最も単純な、0~1の範囲の連続的な確率変数Rを考えます。そして確率はどの場所も一様であるとします。
この場合は、確率密度関数は、

f\left( x \right) =1\quad \left( 0\le x<1 \right) 

となります。この確率変数Rが、ある値r以下になる確率は、

P\left( 0\le R<r \right) =\int _{ 0 }^{ r }{ 1dt } = [t]^r_0　= r\quad \left( 0\le r<1 \right) 

という式で表せます。これは具体的に、0.5以下になる確率はやはり0.5だし、0.1以下になる確率はやはり0.1というのは、直観的にも明らかです。
この辺で確認ですが、目的の確率変数はXであり、これはある確率密度関数f(x)を持ち、累積分布関数はF(x)であるとします。

P\left( x\le X<x+\delta x \right) =f\left( x \right) \delta x\\ P\left( 0\le X<x \right) =\int _{ 0 }^{ x }{ f(t)dt } =F(x)

次にちょっと横道にそれますが、不等式を変形します。

0\le R<r\\ F^{ -1 }\left( 0 \right) \le F^{ -1 }\left( R \right) <F^{ -1 }\left( r \right) \\ 0\le F^{ -1 }\left( R \right) <F^{ -1 }\left( r \right) 

それぞれ累積分布関数の逆関数を通します。そして、やはり通しても確率はrのままです。

P\left( 0\le F^{ -1 }\left( R \right) <F^{ -1 }\left( r \right)  \right) =r\\ 

ここで、適当に以下のように名前をつけます。

F^{ -1 }\left( r \right) =v\\ r=F(v)

すると確率の式は、

P\left( 0\le F^{ -1 }\left( R \right) <v\right) = F(v)

となりますね、
ところでこれ、Pの不等式の真ん中を確率変数Xだと見立てると、

P\left( 0\le F^{ -1 }\left( R \right) <v \right) =F(v)\\ P\left( 0\le X<x \right) =F(x)\\ X=F^{ -1 }\left( R \right) 

なんと、いつの間にか確率変数Xと、一様の確率変数Rとの関係性が導き出されてしまいました。
つまるところ、任意の確率密度関数を積分した関数の逆関数を、一様乱数に噛ませれば任意の確率密度を持つ確率変数を得ることができる、ということです。
これを逆関数法と呼びます。

実際にやってみる

さて、考え方はわかりましたので、具体的に作ってみましょう。

0~2の範囲で一様分布する乱数

これはもう直観的に0~1の乱数を2倍するだけなんですが、逆関数法で同じ答えがでるかを確かめます。
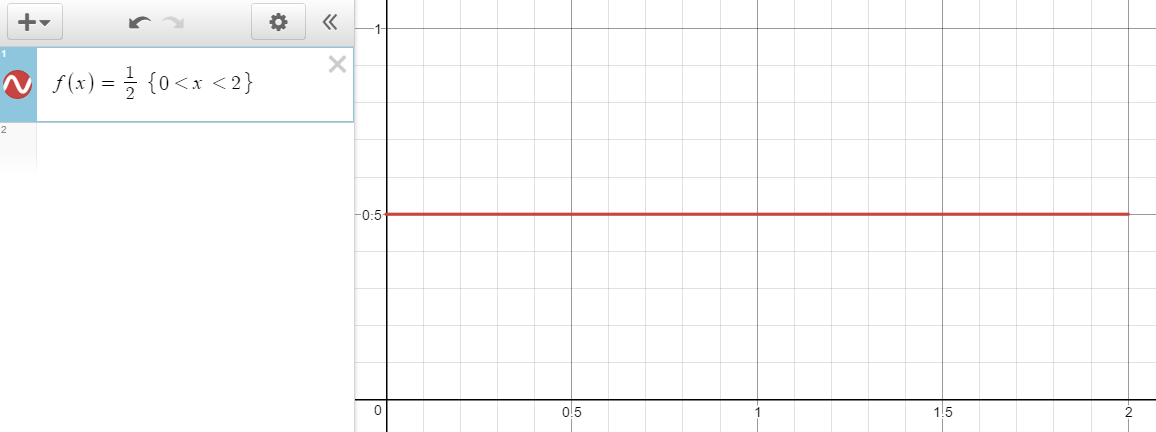
まずは確率密度関数です。
これは以下のようになります。

f\left( x \right) =\frac { 1 }{ 2 } 

0~2の範囲で積分して1にするために、1/2となっています。

F\left( x \right) =\int _{ 0 }^{ x }{ f(t)dt } =\int _{ 0 }^{ x }{ \frac { 1 }{ 2 } dt } =[\frac { 1 }{ 2 } t]^{ x }_{ 0 }\\ =\frac { 1 }{ 2 } x

逆関数を求めます。数3の範疇ですが、F(x) をxに、xをF^-1(x)に置き換えて解けば良いだけです。

F\left( x \right) =\frac { 1 }{ 2 } x\\ x=\frac { 1 }{ 2 } F^{ -1 }\left( x \right) \\ F^{ -1 }\left( x \right) =2x

やはり逆関数法を使っても、２倍すればいいということが示されました。

三角形に分布する乱数

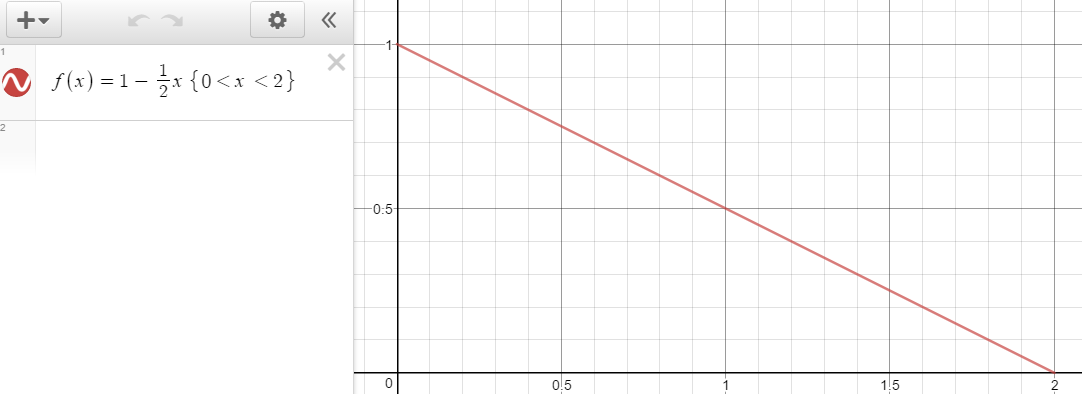
今度はこういう確率密度関数はどうでしょうか？

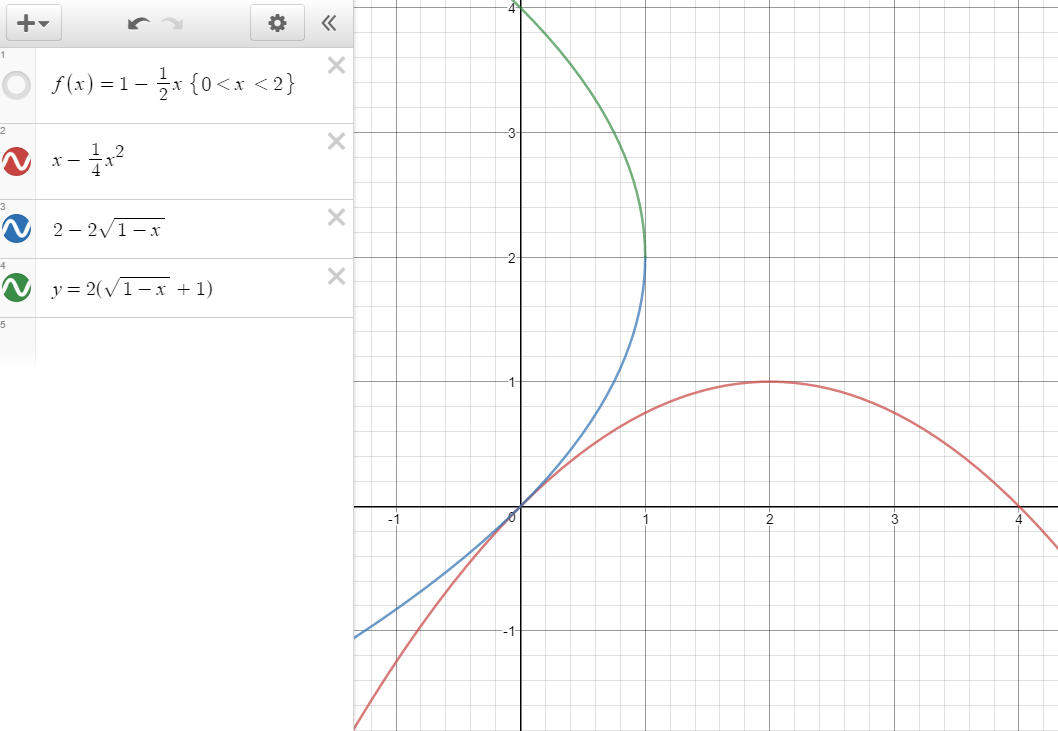
f\left( x \right) =1-\frac { 1 }{ 2 } x

残念ながら即座にはわかりません。でも逆関数法なら、簡単です。

F(x)=\int _{ 0 }^{ x }{ 1-\frac { 1 }{ 2 } tdt= } \int _{ 0 }^{ x }{ 1dt-\int _{ 0 }^{ x }{ \frac { 1 }{ 2 } tdt } = } [t]^{ x }_{ 0 }-[\frac { 1 }{ 4 } { t }^{ 2 }]^{ x }_{ 0 }=x-\frac { 1 }{ 4 } { x }^{ 2 }\\ F(x)=x-\frac { 1 }{ 4 } { x }^{ 2 }\\ F^{ -1 }\left( x \right) =y\\ x=y-{ \frac { 1 }{ 4 } { y }^{ 2 } }\\ 4x=4y-{ y }^{ 2 }\\ -4x=-4y+{ y }^{ 2 }\\ -4x={ (2-y) }^{ 2 }-4\\ -4x+4={ (2-y) }^{ 2 }\\ \pm \sqrt { -4x+4 } =2-y\\ \pm \sqrt { 4(-x+1) } -2=-y\\ \pm 2\sqrt { 1-x } -2=-y\\ -y=\pm 2\sqrt { 1-x } -2\\ y=2\pm 2\sqrt { 1-x } \\ F^{ -1 }\left( x \right) =2\pm 2\sqrt { 1-x } \\ F^{ -1 }\left( x \right) =2-2\sqrt { 1-x } \quad \quad (0<F^{ -1 }\left( x \right) <2)

横着したい方は、Wolframに投げちゃっても良いでしょう

出てきた逆関数のグラフはこうなります。逆関数の性質より、きれいにy=xで折り返した形になっています

これをもとにC++で乱数を実際に生成してみます。

#include <cmath>
#include <random>
#include <iostream>
#include <stdlib.h>

int main()
{
    FILE *f = fopen("data.txt", "w");
    std::mt19937 mt;
    std::uniform_real_distribution<double> uniform_01(0.0, 1.0);

    for (int i = 0; i < 50000; ++i)
    {
        double r = uniform_01(mt);
        double x = 2.0 - 2.0 * std::sqrt(1.0 - r);
        fprintf(f, "%.20f\n", x);
    }
    fclose(f);
    return 0;
}

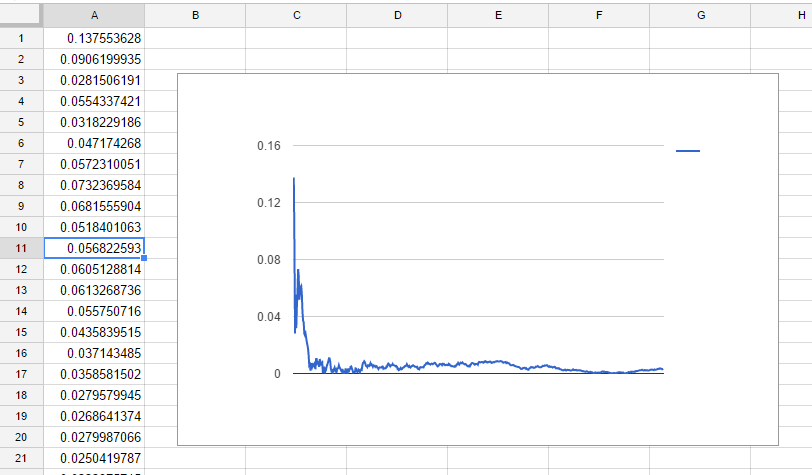
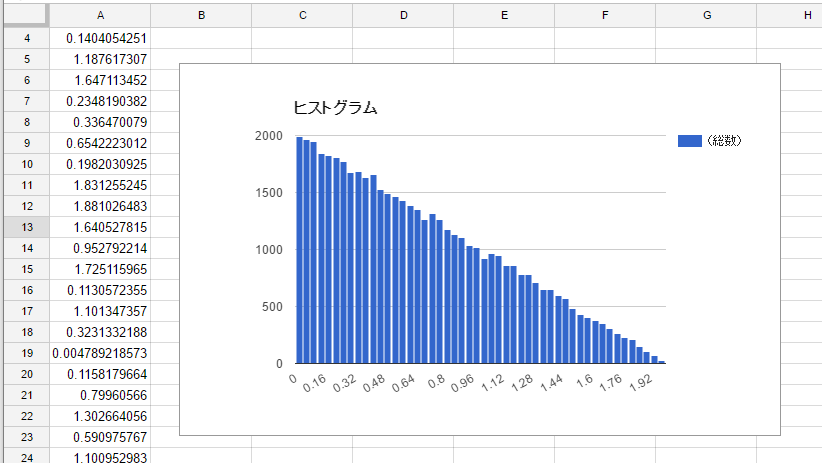
ヒストグラムを出してみましょう。とりあえずgoogle spreadsheetでやりました。

見事に任意の確率密度の乱数を作り出すことができています。

モンテカルロ積分

さて、そろそろモンテカルロ積分の話にうつります。
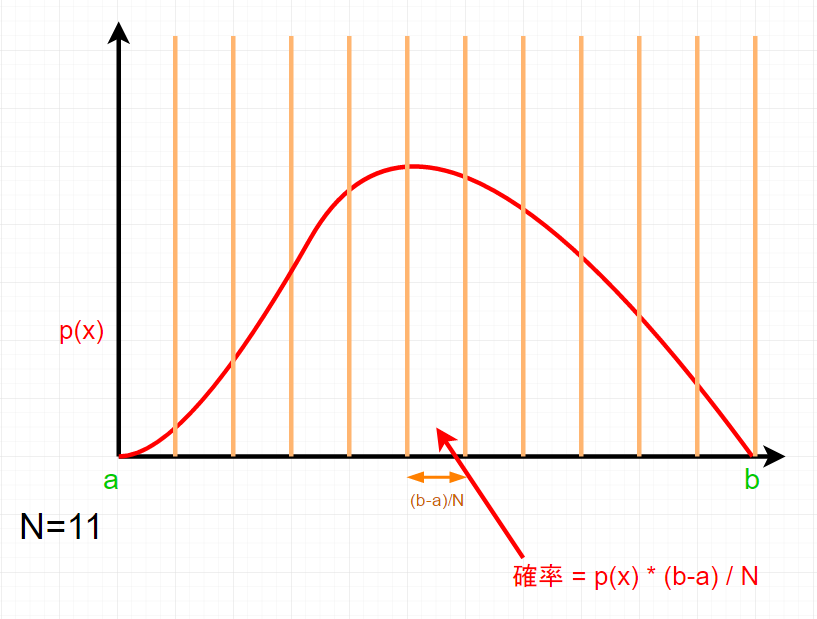
定積分の数値計算をする愚直なアイディアでは、積分区間を細かく区切ってf(x)を評価し区切った幅をかけて、合計するというのがあります。

\int _{ a }^{ b }{ f(x)dx= } \sum _{ k=1 }^{ N }{ f(x_{ k }) } \frac { (b-a) }{ N } \\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ f(x_{ k }) } 

どこの短冊を評価するか？に乱数を使ったのがモンテカルロ積分であるとも言えます。
積分区間に一様な確率変数Xを使った定積分は以下のようになります。

\int _{ a }^{ b }{ f(x)dx= } \sum _{ k=1 }^{ N }{ f(X_{ k }) } \frac { (b-a) }{ N } \\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ f(X_{ k }) } 

形がほとんど一緒なので、一見すると正しそうです。
でも本当に乱数を使っても、計算結果は正しいといえるんでしょうか？
そこで期待値を考えます。

E[\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ f(X_{ k }) } ]\quad =\quad ?

期待値の数式をいじるとき、期待値の線形性という性質が役に立ちます。
こちらのサイトが十二分にわかりやすいです。
期待値というのは、期待値を考えてから足しあわあせても、足し合わせてから期待値を考えても、どちらも正しいということです。

E[A+B]=E[A]+E[B]

ついでに、

E[2A]=E[A+A]=E[A]+E[A]=2E(A)

みたいなのだって成り立ちます。
もっというと、任意の定数α, βに対して、

E[αA+βB]=αE[A]+βE[B]

も許されています。
なので、

E[\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ f(X_{ k }) } ]=\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ E[f(X_{ k }) } ]

と変形できます。

さて、

E[f(X_{ k })]

これってこのあとどうしたらいいでしょうか？
期待値というのは、それぞれのパターンが出たときの値と、その確率をかけ合わせて、全パターン分足して計算するものでした。
例えば、

サイコロの目	点数	確率
1, 2	10	1/3
3, 4	20	1/3
5, 6	30	1/3

のようなゲームは、

E[ゲームの点数]=10\cdot \frac { 1 }{ 3 } +20\cdot \frac { 1 }{ 3 } +30\cdot \frac { 1 }{ 3 } =\frac { 1 }{ 3 } (10+20+30)=\frac { 60 }{ 3 } =20

と計算するのでした。
では今回のような連続的な確率変数に対しての確率はどうだろうか・・・？
おっと、もうすでに上でやっていました。確率密度関数の出番のようです。

P\left( x\le X<x+\delta x \right) = p\left( x \right) \delta x \\
P\left( a\le X\le b \right) =\int _{ a }^{ b }{ p\left( x \right) dx }

文字として被積分関数がfなので、確率密度関数はpとしました。
つまり確率密度関数は、定積分すると、その区間にXが当たる確率を返すのでした。
なので、期待値を考えるなら、Xの取りうる範囲、区間a~bを細かく区切ってf(x)を評価し、確率をかけて、合計すれば良いということになります。

区切った区間それぞれの確率は、このように考える事ができます。

P\left( r\le X\le r+\frac { (b-a) }{ N }  \right) =p\left( r \right) \frac { (b-a) }{ N } 

そのことから考えて、f(X)の期待値は、

E[f(X_{ k })]=\sum _{ k=1 }^{ N }{ f(X_{ k }) } p(X_{ k })\frac { (b-a) }{ N } \quad \quad \quad (a\le X<b)

・・・おや、よくよく考えると、Nを大きくしていったら、これは積分と言えそうです。
積分記号はもともとSUMから来たものでした。
というわけでここまできました。

E[\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ f(X_{ k }) } ]\\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ E[f(X_{ k }) } ]\\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ f\left( x \right) p\left( x \right)  } dx } 

ここで確率変数Xは一様分布のため、

p\left( x \right) =\frac { 1 }{ b-a } 

です。これはもちろん確率密度関数が、全区間で積分すると１になるためでした。

E[\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ f(X_{ k }) } ]\\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ E[f(X_{ k }) } ]\\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ f\left( x \right) p\left( x \right)  } dx } \\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ f\left( x \right) \frac { 1 }{ (b-a) }  } dx } \\ =\frac { (b-a) }{ N } \sum _{ k=1 }^{ N }{ \frac { 1 }{ (b-a) } \int _{ a }^{ b }{ f\left( x \right)  } dx } \\ =\frac { (b-a) }{ N } \cdot \frac { 1 }{ (b-a) } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ f\left( x \right)  } dx } \\ =\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ f\left( x \right)  } dx } \\ =\int _{ a }^{ b }{ f\left( x \right)  } dx

最後のは、N回同じものを足して、Nで割っているだけなので、そのまま消します。
これでたしかに期待値が積分の真の値であることが示せました。

任意の確率分布を使う

上のパートでは、一様分布する乱数を使っての積分を考えました。でもちょっとした工夫で、もっと柔軟にできます。それは任意の確率分布の乱数を使うことです。
任意の確率密度関数p(x)の確率分布をもつXを使った積分は、

\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ \frac { f(X_{ k }) }{ p\left( X_{ k } \right)  }  } 

となります。本当でしょうか？
ちょっと見づらいので、

\frac { f(x) }{ p\left( x \right)  } =g(x)

といったんおきます。
そして期待値はどうなるでしょうか。

E[\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ \frac { f(X_{ k }) }{ p\left( X_{ k } \right)  }  } ]=\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ E[\frac { f(X_{ k }) }{ p\left( X_{ k } \right)  }  } ]\\ =\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ E[g\left( X_{ k } \right) ] } \\ =\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ g\left( x \right) p\left( x \right) dx }  } \\ =\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ \frac { f(x) }{ p\left( x \right)  } p\left( x \right) dx }  } \\ =\frac { 1 }{ N } \sum _{ k=1 }^{ N }{ \int _{ a }^{ b }{ f\left( x \right) dx }  } \\ =\int _{ a }^{ b }{ f\left( x \right) dx } 

なんと、やはり期待値は定積分の値に一致しました。
これが何に使えるかといえば、乱数を使って積分するときに、ほとんど数字がゼロの場所を減らし、数値が大きいところを重点的に計算に反映させることで、一様分布よりも少ないサンプルでより正確な積分を行うことが可能になるということです。

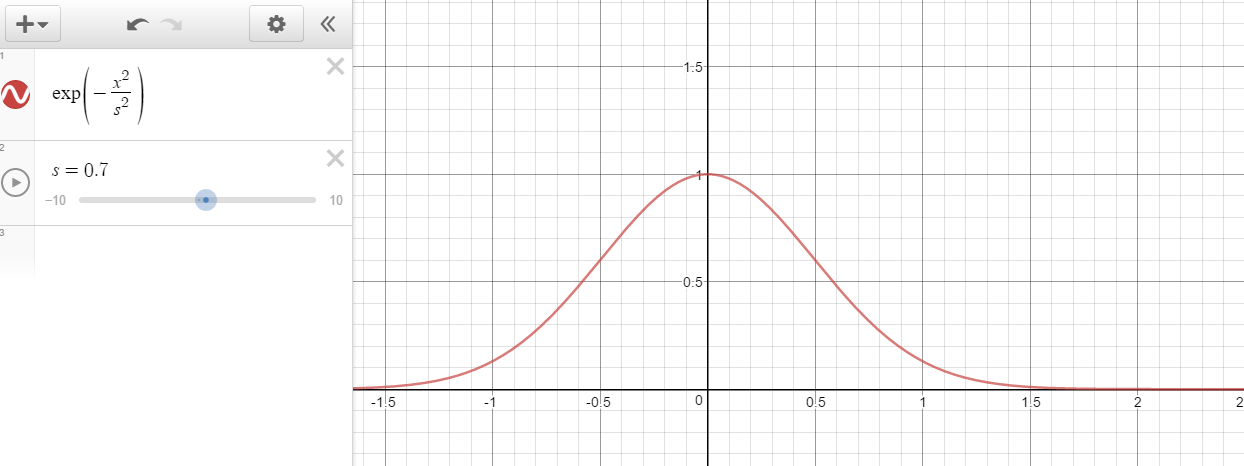
例えば、このような

中心部がわりと数字が大きく、0から遠くなればなるほど、ほとんど数字が0に近づいています。
このような関数の積分においては、一様分布の乱数ではとても不利で、
もし原点に近くを多くヒットできる確率密度関数が用意できて、かつそれに従う乱数が用意できれば、数段積分の精度があがることでしょう。

このテクニックのことを重点サンプリングとよび、レイトレーシングではBRDFやIBLの重点サンプリングで応用されています。

試してみる

最後に、上でせっかく作った確率密度で、上の関数を積分してみましょう。

f\left(x\right)\ =\exp \left(-\frac{x^2}{0.5}\right) \\
p\left(x\right)=1-\frac{1}{2}x

検算用に、wolframに解析解を求めてもらいました。

サクッと実装します。
ここでは、真値との差を出力しました。

#include <cmath>
#include <random>
#include <iostream>
#include <stdlib.h>

inline double f(double x) {
    return std::exp(-x*x / (0.5));
}

inline double p(double x) {
    return 1.0 - 0.5 * x;
}
inline double inverse_of_cdf(double x) {
    return 2.0 - 2.0 * std::sqrt(1.0 - x);
}

int main()
{
    std::mt19937 mt;
    std::uniform_real_distribution<double> uniform_01(0.0, 1.0);

    double sum = 0.0;
    int N = 6000;
    for (int i = 0; i < N; ++i)
    {
        if (i != 0 && i % 10 == 0) {
            double ans = sum / i;
            printf("%.10f\n", std::fabs(ans - 0.626617));
        }

        double r = uniform_01(mt);
        double x = inverse_of_cdf(r);
        double value = f(x) / p(x);
        sum += value;
    }

    return 0;
}

なるほど、確かにサンプルが増えると真の値に近づいていっています。
なかなかうまくいっているようです。

まとめ

今回のトピックはだいぶレイを飛ばすこともなく地味な部分ですが、とても重要な基盤部分だと思います。
あやふやにせず、きっちり数式を通じて理解しておきたいところです。
個人的に確率密度関数の割り算がなかなか納得できなく、公式をブラックボックスで使う状態だったのですが、
最近ようやくぼちぼち理解が追いついてきた感があります。同じような悩みを抱えている方がいらっしゃいましたらこの記事が一助となれば幸いです。