DQNの生い立ち ＋ Deep Q-NetworkをChainerで書いた

#はじめに
そもそもDQNが作りたかったわけじゃなくて、他の目的でChainerを使いたかったのでその練習にDQNを書いたんですが、せっかくだし公開しようと思いました 公開しました 。またどうせ公開するなら、この機会にこれ（Q学習+関数近似）関連で持っている知識をついでに整理しようと思ってまとめました。

　ニュース記事とかNatureとかNIPSの論文だけ読むと、DQN作ったDeepmind/Googleすげー！！！って感覚になりそうですが、強化学習的な歴史的経緯を考えると強化学習+深層学習になった、むしろかなり当然の成り行きで生まれた技術であることがわかります。（ATARIのゲームを人間以上のパフォーマンスでプレイするというのがビジュアル的にわかりやすかった$\leftrightarrow$問題設定が良かったというのもあります。）

　この記事ではNIPSとNatureの以下の２本の論文

・ V. Mnih et al., "Playing atari with deep reinforcement learning"
　　http://arxiv.org/pdf/1312.5602.pdf
・ V. Mnih et al., "Human-level control through deep reinforcement learning"
　　http://www.nature.com/nature/journal/v518/n7540/abs/nature14236.html

について、そこにいたるまでの強化学習の経緯をなるべく関係するところだけを取り上げて解説するつもりです。

　オタクな追っかけ的情報ですが、筆頭著者のMnihさんはUCTをはじめ確率的プランニングで有名なSzepesvári先生と、おなじみニューラルネットワークのゴッドファーザー、Hinton先生の元で学んだ人で、DQNが生まれたのは自然な流れといえるでしょう。

#ていうか、強化学習って？
強化学習自体、聞きなれない方もいるかもしれません。Bishop先生の"PRML"とか、最近だとMurphy先生の"Machine Learning"とかでも「本書では機械学習の多くの分野を扱う。ただし強化学習は除く。」のような扱いになっています。

　これは、強化学習の特殊な条件設定のためだと思います。というのも、強化学習の理論は制御理論（最適制御理論・動的計画法）と機械学習をシェイカーに入れて力いっぱいかき混ぜたものになっているからです。ここではそういった理論に立ち入ることなく、「強化学習って何するのよ？」という事をできるだけ簡単に説明します（するつもりです）。

##強化学習：環境とエージェント
　強化学習とは、"環境"中に置かれた"エージェント"が、環境との相互作用を通して最適な方策（行動を決定するきまり）を得るための機械学習の手法のことを言います。

　Wikipediaによると、「強化学習(きょうかがくしゅう, Reinforcement Learning)とは、ある環境内におけるエージェントが、現在の状態を観測し、取るべき行動を決定する問題を扱う機械学習の一種。」 ¹ だそうです。

　百聞は一見にしかずというやつで、模式図で表すと次の図のようになります。

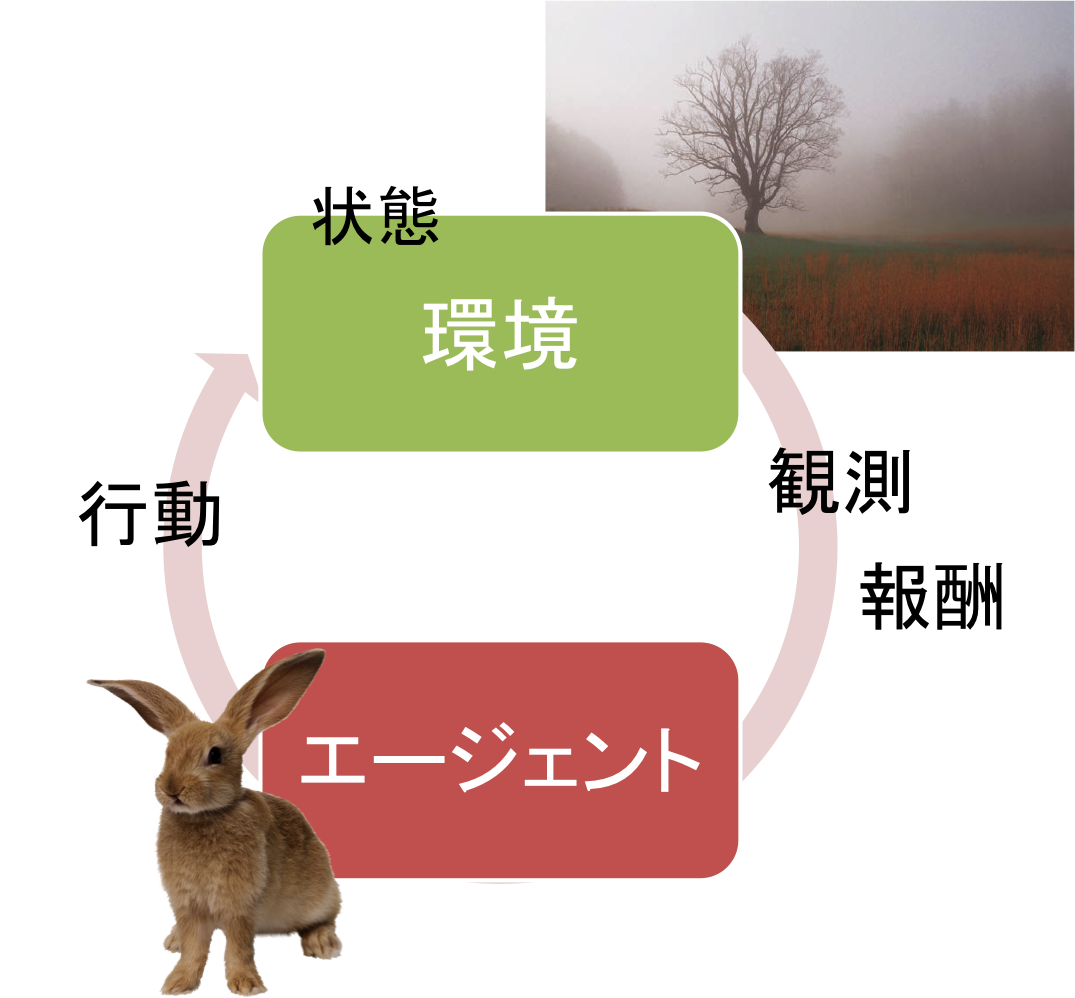
強化学習は次の単純なステップを繰り返すことで時間が進行していきます。

1. エージェントは環境から受け取った観測 $o$（あるいは直接、環境の状態 $s$ ）を受け取り、方策 $\pi$ に基いて環境に行動 $a$ を返す。
2. 環境はエージェントから受け取った行動 $a$ と現在の状態 $s$ に基いて、次の状態 $s'$ に変化し、その遷移に基いて次の観測 $o'$ と、報酬 $r$ と呼ばれる直前の行動の良し悪しを示す1つの数（スカラー量）をエージェントに返す。
3. 時間の進行：$t \leftarrow t + 1$

ここで $\leftarrow$ は代入操作を表します。報酬は通常、状態と行動、そして次の状態の関数で与えられます $r=r(s,a,s')$。我々は強化学習の条件から、環境を直接操作するといったことはできません。我々が自由に操作できるのは、あくまでエージェントのみです。このような環境とエージェントの相互作用、そして制約が、強化学習の置かれた特殊性を表しています。

　ここでは簡単のため、観測は環境の状態が直接エージェントに渡される状況（ $o=s$ ）についてのみ説明します ² 。強化学習の枠組みにおいてエージェントにとって最適な方策とは、その方策に従って行動を決定していくことで、現時点から無限の未来までに得ることのできる報酬の和

R_t = \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} = r_{t+1} + \gamma\ r_{t+2} + \gamma^2\ r_{t+3} + \cdots

を最大化させるような方策であると考えます。すなわちこれが強化学習における目的関数です。$t$ は現時刻、$r_i$ は時刻 $i$ でエージェントが受け取る報酬を表します。$\gamma$ は割引率と呼ばれる強化学習のパラメータです。この値は通常 $0$ 以上 $1$ 未満の連続値で与えるもので、無限大・無限小を含まないどのような報酬設定に対しても $R_t$ が有限の値になるように導入される定数です。たいてい、$\gamma = 0.99$などといった$1$に近い値に設定します。

　今のように環境の状態がエージェントの観測として直接渡される（ $o=s$ ）場合は必ず、行動を出力とするある決定論的な関数 $\pi^* (s)$ で表すことが可能な最適方策が、少なくとも1つ存在することが理論的に知られています³。詳細は割愛しますが、以下の節で紹介する学習手法はいずれも上記の目的関数を最大化させる決定論的な方策を探す手法という点で同じものです。

　なおDQNがATARIゲームを学習する場合、4ステップ間のゲーム画面（観測）をもって状態が構成されると仮定して学習を行っています。

#Deep Q-Network出生以前
ここではDeep Q-Networkが生まれた背景について紹介していきます。Deep Q-Networkを構成するQ学習、関数近似、Experience Replay（経験再生）、さらにNeural Fitted Q Iterationについて説明します。

##Q学習
Q学習は強化学習の古典的なアルゴリズムで、強化学習のアルゴリズムでは最も広く知られた存在かもしれません。Q学習に基づく手法では、みな 最適行動価値関数 と呼ばれる関数を近似することで最適方策を学習します。

　最適行動価値は各状態と行動の組 $(s,a)$ にそれぞれ１つ存在し、「状態 $s$ で行動 $a$ を取り、残りはずっと最適方策に従ったとした場合に得る報酬の和（即ち目的関数） $R$の期待値」を表す値です。これを全ての各状態と行動の組 $(s,a)$について求めたものを最適行動価値関数と呼び、 $Q^* (s,a)$ で表します。

　ややこしい定義ですが、この値はざっくり言うと、エージェントが置かれた状態 $s$ で行動 $a$ を取るメリット を表します。この最適行動価値関数に関して重要な点は、この関数と最適な決定論的方策（のうちの1つである） $ \pi ^* (s)$ との間には

\pi^*(s) = \rm{argmax}_a Q^* (s,a)  

**の関係があるということです。**すなわち、Q学習において ⁴ 最適行動価値関数を得ることと最適方策を得ることは、ほぼ同じ意味を持つのです。

　実際のQ学習ではすべての状態 $s$ と行動の組 $a$ に対してテーブル関数 $Q(s,a)$ を作成し、すべての要素を任意の値に初期化した後、毎回のデータ ($s$, $a$, $r$, $s'$) に対して次の式で更新します。

Q(s,a) \leftarrow (1-\alpha) Q(s,a) + \alpha \Bigl(r + \gamma \ \max_{a'} Q(s',a')\Bigr)

ここで $r$ は状態 $s$ で行動 $a$ を選択したあと環境から受け取った報酬、$s'$ は同様に状態 $s$ で行動 $a$ を選択した後、次の時刻で受け取った状態を表します。$\alpha$ は学習率を表します。通常は $1$ 未満の $0.1$ や $0.01$ といった小さい値を使います。このアルゴリズムは $Q(s,a)$ を、毎回その関数自身を含む $r + \gamma \ \max_{a'} Q(s',a')$ に毎回少しづつ近づけていく形になっています⁵。

　上の更新式の表記は（特にSutton & Barto本で強化学習を知られた方には）あまり強化学習ではポピュラーではないかもしれませんが、この表記は価値関数 $Q(s,a)$ を何に当てはめようとしているのかを明示的に表す形式になっています。当然、この更新式はよりポピュラーな表記である

Q(s,a) \leftarrow Q(s,a) + \alpha \Bigl(r + \gamma\ \max_{a'} Q(s',a') - Q(s,a)\Bigr)

と等価です。

　Q学習の最大の特徴は、($s$, $a$) の全ての組からサンプル ($s$, $a$, $r$, $s'$) が無限回得られるとするなら、それらをどのような順番で与えたとしても上記のアルゴリズムで必ず最適な価値関数 $Q^*(s,a)$ が得られるという点にあります⁶。この特徴は後で紹介するExperience Replayで最大限に利用されます。　

　すべての状態と行動についてテーブル関数 $Q(s,a)$ を作成するとは言いましたが、例えばDQNのように画像列などのむちゃくちゃに高次元なものを状態として与えたりすると、当然テーブル関数ではとてもメモリに乗りませんし、すべてサンプルを取ることなんて出来ません。 $10\times 10$のバイナリ画像でも $2^{100} \approx 10^{30} $ といったとても手に負えない状態数になってしまいます。そこで、こういった非常に高次元の状態を扱う場合には $Q(s,a)$ に関数近似を使います。

##DeepじゃないQ-network：Q学習 ＋ 関数近似
というわけで、関数 $Q(s,a)$ に関数近似を使うことを考えます。そこで $Q(s,a)$ が何らかのパラメータ $\theta$ を用いて表されていて、近似された関数を $Q_\theta(s,a)$ で表すことにします。

　この関数を用いてQ学習に相当する関数を近似するには、古典的には以下の勾配法によるアルゴリズムを使います。

\theta \leftarrow \theta - \alpha \nabla_\theta L_\theta

ここで $L_\theta$ は以下の誤差関数で表されます。このへんは一般的な、勾配法での更新とおんなじです。

L_\theta = \frac{1}{2}\Bigl( \rm{target} - Q_\theta(s,a)\Bigr)^2

ところで、真の行動価値 $Q^* (s,a)$ がわかっていれば純粋な教師あり学習として $\rm{target} = Q^* (s,a)$ とすれば良いのですが、強化学習では教師信号にあたる $Q^* (s,a)$ は与えられません。そこでテーブル関数を用いたQ学習と同様に

 \rm{target} = r + \gamma \max_{a'} Q_\theta (s',a')

をその時点での教師信号として使います。そして誤差関数の微分は、あくまで $Q_\theta(s,a)$ を教師信号に近づけるためとして、教師信号に対する微分は行いません。つまり

\begin{align}
\nabla_\theta L_\theta &=-\Bigl(\rm{target} - Q_\theta(s,a)\Bigr) \nabla_\theta Q_\theta(s,a)\\
&=-\Bigl(r + \gamma \max_{a'} Q_\theta (s',a') - Q_\theta(s,a)\Bigr) \nabla_\theta Q_\theta(s,a)
\end{align}

となります。

　結果、近似関数を用いた場合のQ学習は以下のようになります。

\theta \leftarrow \theta + \alpha \Bigl(r + \gamma \max_{a'} Q_\theta (s',a') - Q_\theta(s,a)\Bigr) \nabla_\theta Q_\theta(s,a)

テーブル関数を用いたQ学習の２つ目の更新式にとても良く似た式が現れました。

　関数近似を用いたQ学習で気をつけなければいけないことは、誤差関数の微分の計算において教師信号に含まれる $\max_{a'} Q_\theta (s',a')$ を微分してはならないということです。自分で微分してコードに落とすようなときはこのような間違いはまず起こりませんが、最近広く使われる自動微分を利用すると、知らない間に教師信号まで含めて微分してしまっているという事が起こりえます（しかも、学習初期は両者おんなじような感じで動くので気付きにくい）。(自分も一度やりました ﾎﾞｿｯ)

　教師信号まで含めて微分して学習させてしまうと、ここで述べた関数近似器を用いたQ学習とは異なる性質を持つアルゴリズムになってしまいます。

###関数近似にニューラルネットワークを使う
多層のニューラルネットワークのような非線形関数近似手法を用いたQ学習は、誤差逆伝播法が開発された第二次ニューラルネットワークの時代、強化学習が理論的に成熟し始めた時期に、Long-Ji Linさんという方が精力的に行いました。Experience Replayはこの方が論文"Self-Improving Reactive Agents Based On Reinforcement Learning, Planning and Teaching " で公開した手法です。

　余談ですが、この論文は複雑でダイナミックなシミュレーション環境中で、なんとか生き残ろうとするエージェントを学習させるというとても面白い論文になっています。

　多層（といっても全結合の3層か4層程度）ニューラルネットワークではどうしても学習が遅く、また学習率を大きくしても学習が発散してしまいます。これをなんとか高速化する方法として、上記で述べたQ学習の特性を利用します。

　Experience Replayとはエージェントが経験したサンプル ($s$, $a$, $r$, $s'$）を全て（あるいは有限の時間数ぶん）記録しておき、一度つかったサンプルを上記の関数近似を用いたQ学習で何度も利用するという手法です。これは、テーブル関数を用いたQ学習ではサンプルの順番をどのように並べ替えても学習は進行するので、関数近似器を使ったQ学習でも同様の性質を期待するという考え方になっています。

　Experience Replayのある種の極限を考えるようなアルゴリズムが、Riedmiller先生のNeural Fitted Q Iteration ⁷です。これはここまでの「自分でデータを集めて、学習する」といったオンラインの強化学習とは異なり、まずサンプル ($s$, $a$, $r$, $s'$）からなる十分な数のデータがあるものとして、「これ以上サンプルを追加せず、与えられたデータから最適方策を学習する」、すなわちバッチ強化学習を行うことを考えるアルゴリズムです。

　Neural Fitted Q Iterationのアルゴリズムの擬似コードは以下のようになります。

input: 多数のサンプル（$s$, $a$, $r$, $s'$）からなるデータ $D$
output: 学習後のQ関数 $Q_{\theta_N} (s,a)$

1. $k=0$
2. ニューラルネットワークのパラメータ $\theta_0$ を初期化する
3. 繰り返し： $N-1$ 回繰り返す
4. 　　　　データ $D$ からサンプルを $M$ 個取り出す
   5.　　　　 $M$個のサンプルを元に、
   　　　　　　　 教師信号 $ {\rm{target}}^t = r_t + \gamma \max_{a'} Q_{\theta_k} (s_t',a') $ と
   　　 　　　　　入力 $ (s_t, a_t) $ を作成する（ $t=1,2,...,M$ ）
   6.　　　　 作成した教師信号 ${\rm{target}}^t$ と入力$ (s_t, a_t) $を元に、
   　　　　　 $Q_\theta (s, a)$ と教師信号との誤差$L_\theta$ を何らかの勾配法で最小化
   　　　　　 する。学習が収束するなり一定の条件を満たしたら、その結果を
   　　　　　 $\theta_{k+1}$とする
   7.　　　　 $k \leftarrow k+1$とする
5. $Q_{\theta_N} (s,a)$ を返す

Neural Fitted Q Iterationで重要な点は、繰り返し中の各回に行われる勾配法を使った最適化において、教師信号は常に同じパラメータ $\theta_k$ に基づく $r+\max_{a'} Q_{\theta_k} (s_t',a') $ から生成されていて、そのためオンライン手法とは異なり、各最適化中では完全に教師あり学習になっているところです。そのため、設定的には非常に学習が安定したものとなると期待されます。

　Neural Fitted Q Iterationはデータ数が一定として、そこから情報を引き出すアルゴリズムですが、さらに発展的な手法で、ある程度学習を行った後にエージェントを環境中で動かし、バッチのデータを後から追加していくGrowing Batchという考え方が提案されています ⁸ 。ここまでくるとほとんど手法的にはNature論文のものと変わらないです。

　Riedmiller先生のチームはこのバッチ強化学習を主な手法として、ロボットの行動学習などに適用しています。先生もDeepmindに籍をおいているようで、驚くほど多くの強化学習研究者がDeepmindに集積されていることが伺えます。

#そしてDeep Q-Network：Q学習 ＋ 深層学習
　「DQNの何が新しい技術なのか？」という問いは、「以上の強化学習の関数近似に深層学習の技術を適用した」という点に尽きます。

　具体的には、NIPSとNatureの両方での論文で畳み込みニューラルネットワークが用いられていますが、この構造を使用したこと。それと近年開発されたRMSPropを始め、局所解にはまらない最適化手法を適用したこと。これらが本質的にDQNにおいて新しい点と言えます。
（追記：ネットワークに対して状態のみを入力として、その状態における全ての行動価値の推定値を一回のforward伝搬で表現するDQNの構造は新しいものだと思うのですが、すみません確信が持てません。）
（追記:$\uparrow$の追記で紹介したDQNの構造ですが，先例がありました。遅くとも2009年の時点で柴田&河野が同様の構造を持った5層の全結合ニューラルネットワークを用いてQ学習を構成し、画像入力を用いた強化学習をAIBOの行動学習タスクに適用しています⁹。）

　DQNが最初に現れたNIPSでの論文"Playing atari with deep reinforcement learning"ではExperience Replayをミニバッチ手法と組み合わせて大規模に使っています。しかしこれでもなお、オンライン強化学習アルゴリズムはまだ不安定なところがあります。

　一方、Natureでの論文"Human-level control through deep reinforcement learning"ではNeural Fitted Q Iteration ＋ Growing Batchを適用することで、オンライン「ほとんどバッチ」強化学習による安定化が図られています。

　私の知っている、DQNの生い立ちはこんなところです。

#DQNをPython + Chainerで書いたよ（コード公開しました）
というわけでDQNをChainerの練習に実装しました。githubで公開予定です。
$\rightarrow$ 公開しました。
https://github.com/ugo-nama-kun/DQN-chainer

　追記１：公開したコードに関してnature/nipsバージョンの両方を公開しました。テストには、強化学習研究でベンチマークなどを行う際によく用いられるRLglueとRLglue Python-codec、ATARIエミュレータとRLglueをつなぐArcade Learning Environment、PythonパッケージにはNumpy、Scipy、そしてモチロンChainerが必要です。GPUでの計算を想定しているので、NVIDIAのGPUが必要です。Ubuntu 14.04LTSでのみ動作確認しています。

　追記２：DQNのExperience Replay用に保存する履歴数を、オリジナルの1/10に設定しています（ $ 10^6 \rightarrow 10^5$ ）。これは単純に、私の小規模なマシンでも動くように規模縮小したかったからです。今回の履歴の実装は、Nature誌中に記載されているアルゴリズムを愚直に実装したものなので非効率的な面があると思います。少なくともPongでは問題なく学習が行われることを確認しています。

　追記3：動作確認は全てATARIゲームのうち、Pongで行っています。他のゲームで学習させる方法はreadme.txtを参照してください。規模縮小しているため、想定されるパフォーマンスが学習されないかもしれません。

　NIPSバージョンとNatureバージョンの両方を作成しましたが、NIPSバージョンは論文中に不明なパラメータも多く、収束の雰囲気はNatureバージョンのほうがよろしい感じです。NIPSバージョンはおまけ程度と考えてください。

Natureバージョンでの学習結果はyoutubeに載せてます $\downarrow$
https://www.youtube.com/watch?v=N813o-Xb6S8

追記：NIPSバージョンの学習もうまくいったので載せました（結果の挙動は殆ど変わりませんが） $\downarrow$
https://www.youtube.com/watch?v=ez_JEHMUpng

　Chainerを使った感想ですが¹⁰、一度TheanoでもDQNを実装してyoutubeに動画を公開をしてみた経験から言うと、ChainerはTheanoベースのものに比べてエラーがどこで発生しているか本当にわかりやすくなっています。かなりの自由度もあるので、ニューラルネットワークのスタンダードなコンポーネントを組み合わせて使うような（畳み込みニューラルネットワークを使いたいとか、層を積んでいきたいとか）使い方ならば断然オススメできます。

　一方でTheanoは、なにか新しいアルゴリズムを試したいとき、ほぼそれがどのようなものでも同じような操作でGPUでの高速化が可能な点がやはり魅力です。例えば「LSTMセルのようなでも別の、もっとイイものを新たに開発してやるぜっ！それをガッツリ最適化するぜ！」って時にはTheanoのような一般的なものを使う必要がでてくる感じがします。こうなるとほとんど先端研究とか学術的（でさらに特殊）な場面で使う感じになりそうですね。以上感想でした。

#Tips：DQNという命名は何故起こったのか？
この話は完全に蛇足になります。

　ヤンキー的な人をDQNと呼ぶほうがどちらかと言うと状況的にまれな現象だと思うのですが、ともかく今回のアルゴリズムがDeep Q-Network = DQNになってマッチングしてしまったのも、結構奇跡的な感じがします。

　それぞれのD-Q-Nのコンポーネントを掘り起こすとDは深層学習（Deep learning）、QはQ学習、Nはニューラルネットワーク（Neural Network）になります。

　まずDeepは昨今の流れ的によしとして（このDeepナントカという呼び方は恐らくHinton先生たちの論文"A fast learning algorithm for deep belief nets"以降から爆発的に増えたという見方がされています。）、Q学習のQは何なんでしょう。強化学習の生みの親のひとり、Barto先生のコメントによると、この"Q"は"Quality"のQ（と思ってるよ）ということらしいです ¹¹ 。

　つぎに、Q-Networkという呼び方はあまり強化学習で一般的でない印象です。論文中でも、だいたい「Q学習で関数近似器にニューラルネットワークを使った」といった言い方がなされている気がします。近い表現は先ほどのLinさんが1993年の論文でQ-netという呼び方をしていて、恐らくこれが今回Q-Networkと呼ばれるようになった源流ではないかと思います。

#注：

1. 強化学習 in Wikipedia
   https://ja.wikipedia.org/wiki/%E5%BC%B7%E5%8C%96%E5%AD%A6%E7%BF%92 ↩

2. このような状況（本当はもう少し色々仮定がありますが）を、「環境はマルコフ決定過程（Markov Decision Process, MDP）で記述できるものと仮定する」などと言います。状態が直接エージェントに渡されない場合は部分観測マルコフ決定過程（Partially Observable Markov Decision Process, POMDP）と呼ばれ、このような環境中での強化学習は近年ではPartially Observable Reinforcement Learning（PORL）などと呼ばれます。ATARIゲームを学習する設定はゲーム画面のみをエージェントの入力としているので当然PORLに含まれますが、4ステップ間のゲーム画面をもって状態が構成されると仮定して学習を行っています。 ↩

3. この点に関して詳しくは M. Putermanの "Markov decision processes" や O . Sigaud, O. Buffetの "Markov decision processes in artificial intelligence" などを参照してください。 ↩

4. より正確には、「マルコフ決定過程で記述できる環境中において」 ↩

5. アルゴリズムの完全な形は次のサイトを参照してください：
   http://webdocs.cs.ualberta.ca/~sutton/book/ebook/node65.html ↩

6. 理論的には、学習率 $\alpha$ がアップデートごとに徐々に減衰していく必要があります。ただし強化学習アルゴリズムを長期間回そうという時や動的な環境にも常にある程度適応させたいといった状況には、あまり現実的ではありません。収束条件に関して詳しくはMelo先生の「Convergence of Q-learning: a simple proof」を参照：
   http://users.isr.ist.utl.pt/~mtjspaan/readingGroup/ProofQlearning.pdf ↩

7. Martin Riedmiller, "Neural fitted Q iteration–first experiences with a data efficient neural reinforcement learning method".
   http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.72.1193&rep=rep1&type=pdf ↩

8. Sascha Lange, Thomas Gabel, and Martin Riedmiller, "Batch reinforcement learning".
   http://ml.informatik.uni-freiburg.de/_media/publications/langegabelriedmiller2011chapter.pdf ↩

9. Katsunari Shibata and Tomohiko Kawano: Learning of Action Generation from Raw Camera Images in a Real-World-like Environment by Simple Coupling of Reinforcement Learning and a Neural Network, Advances in Neuro-Information Processing, Lecture Notes in Computer Science, Proc. of ICONIP (Int'l Conf. on Neural Information Processing) 08, Vol. 5506, pp. 755--762, 55060755.pdf (CD-ROM), 2009 ↩

10. Chainerは公開後も頻繁にアップデートされて新機能が追加されているので、あくまで現在（2015, 7月）の所感です。 ↩

11. ちょっと情報源がマユツバですが：
    http://www.quora.com/How-was-the-term-Q-learning-coined ↩