はじめに
従来の考えでは、パラメータ数を多くすると過学習につながると言われていました。
しかし、近年パラメータ数を多くしても過学習しない現象(二重降下)が発見されました。
今回は二重降下に関連する論文である、
"High-dimensional dynamics of generalization error in neural networks"を紹介します!
本記事はQiita Engineer Festa 2022への投稿です。
目次
- 二重降下とは
- パラメータ数と過学習の関係
- 二重降下が生じる理由
- Eigen gap
- Frozen subspace
- まとめ
二重降下とは
まず、二重降下を紹介します。
二重降下については別の論文(Reconciling modern machine learning practice and the bias-variance trade-off)の図が分かりやすいので、そちらを引用します。
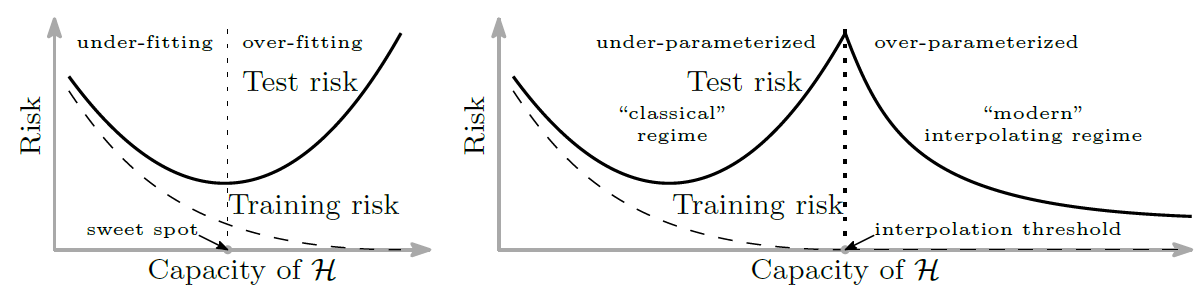
左の図は過学習に関する従来の考えを図にしたものです。
学習を進めていくと学習誤差/汎化誤差ともに下がっていきますが、
ある時を境に汎化誤差が上がっていってしまいます。これが過学習です。
次に二重降下です。
右の図のように、一度上がってしまった汎化誤差がover-parameterized時に下がっています!
つまり、パラメータ数がデータ数より多くても過学習はしないということです。
この不思議な現象が「二重降下(Double Descent)」です。
今回紹介する論文は、この現象が生じる理由をデータ数とパラメータ数の関係から説明しています。
パラメータ数と過学習の関係
パラメータ数と過学習の関係をまとめた図が下記の図です。
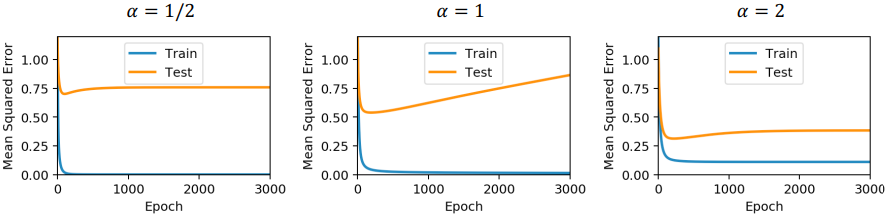
αは「サンプル数(P)/パラメータ数(N)」を表しています。
(Pがサンプル数ってややこしいですね)
これらの内容を整理します。
- 「α=2(サンプル数>パラメータ数)」の時、最も汎化性能が高い。
- 「α=1(サンプル数=パラメータ数)」の時、汎化性能が徐々に悪化している(過学習)。
- 「α=1/2(サンプル数<パラメータ数)」の時、過学習は起きていない(悪化しない)。
従来の考え通り、パラメータ数が少ないときが最も良い汎化性能を出していますね。
一方α=1のときは、徐々に汎化誤差が悪化しています。
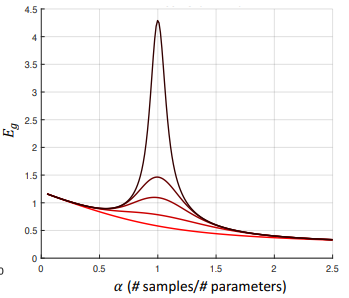
さて、本題の「α=1/2(サンプル数<パラメータ数)」ではどうでしょうか?
「α=2」の時より汎化性能は劣りますが、「α=1」のように汎化性能は悪化していません。
つまり、パラメータ数がデータ数よりも多いときでも、過学習は起きていないのです!
なぜこのようなことが起きるのでしょうか?
二重降下が生じる理由
論文の筆者はこの現象を"Eigen gap"と"Frozen subspace"で説明しています。
Eigen gap
Eigenとは固有値(eigen value)のことで、この固有値の分布が重要です。
なぜなら固有値が過学習に大きな影響を与えるからです。
それを理解するため、下記の式をご覧ください。
これは「学習回数とともに変化する誤差関数」を表す式です。
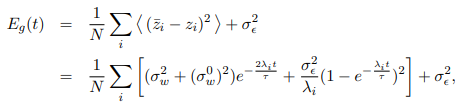
2行目のΣ内の第二項はOverfit noiseを表しており、分母には固有値λがあります。
固有値λの値によってOverfit noiseの大きさ、そして全体の誤差の大きさが決まることが分かります。
それでは、サンプル数とパラメータ数の関係ごとに固有値分布を確認しましょう。
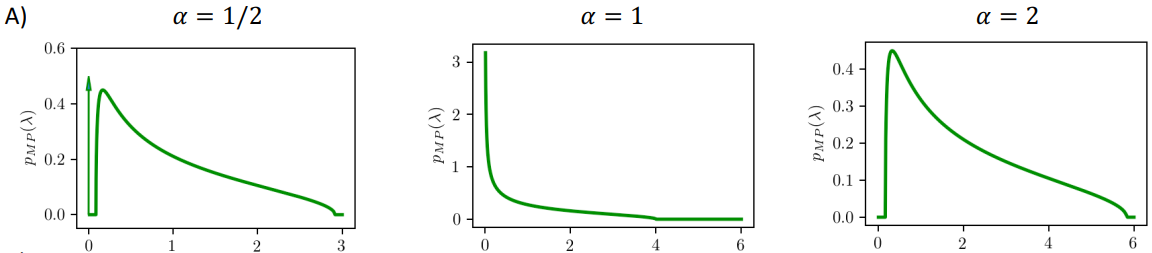
-
「α=1」の固有値分布(過学習が生じるときの分布)
「α=1」の分布では0に限りなく近い値を多くとっています。
これにより先ほどのOverfit noiseが大きくなり、過学習につながったのです。 -
「α=2」の固有値分布(最も汎化性能の高くなるときの分布)
λ=0付近をよく見ると、横棒が見えると思います。
これは固有値λが0に限りなく近い値を取っていない(gapがある)ことを表します。
つまり、「サンプル数>パラメータ数」の時はEigen gapがあり、固有値λが0に近い値をとらず、
Overfit noiseが大きくなりにくかったため、汎化性能が高くなっているのです。
Frozen subspace
最後に、本題の「サンプル数<パラメータ数(α=1/2)」の固有値分布を確認しましょう。
- 「α=1/2」の固有値分布
- Eigen gapがある
- 固有値λが0を取っている。
固有値が0を取ると、学習中に学習が進まないことがあります。
学習が進まないということは、汎化性能はよくならないし、悪くもなりません。
この「学習が進まない」というFrozen subspaceが汎化性能の悪化を防いでいると、筆者は考えています。
まとめ
以上より、パラメータ数がデータ数よりも多いときに過学習が起こらない理由は、
「Eigen gap」と「Frozen subspace」が働いているからと言えます。
この発見は、パラメータ数が増大しやすい画像データなどを扱うときに役立ちそうですね!
本記事はここまでです。
お読みいただきありがとうございました。
P.S.
内容に誤りがございましたら、お手数ですがご指摘いただけますと幸いです。