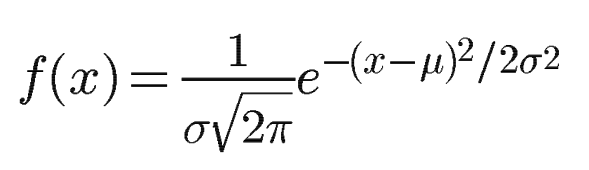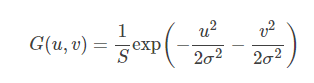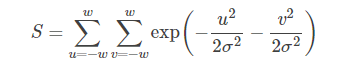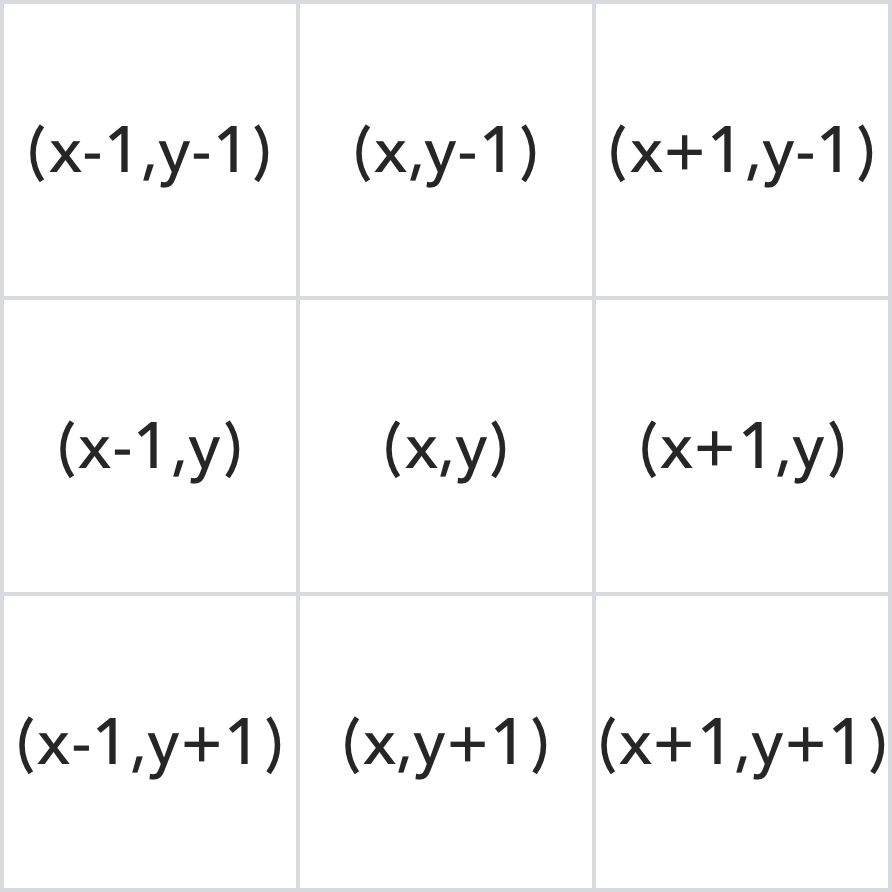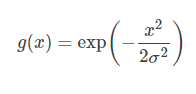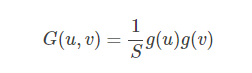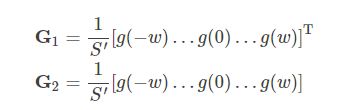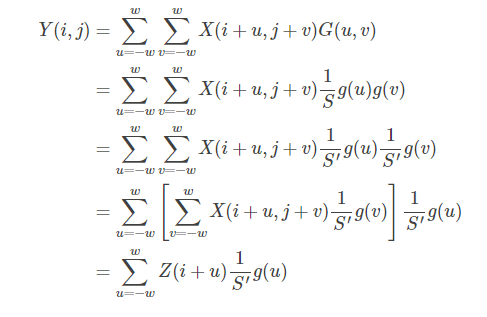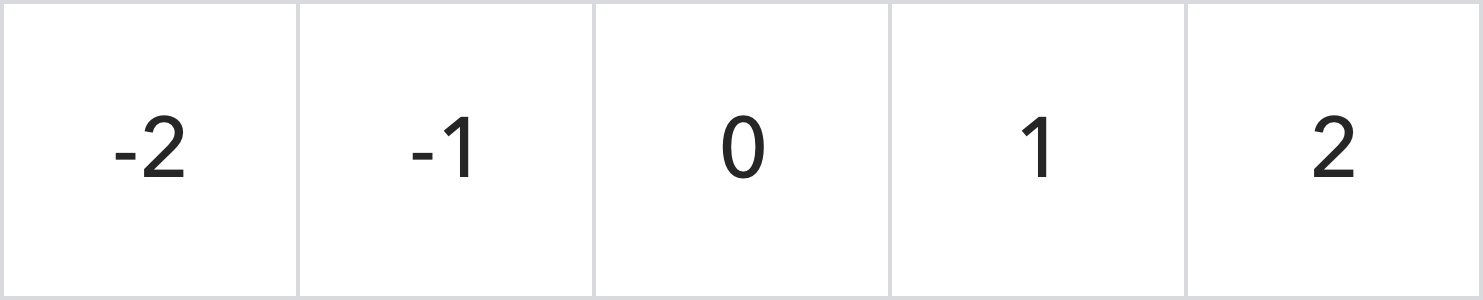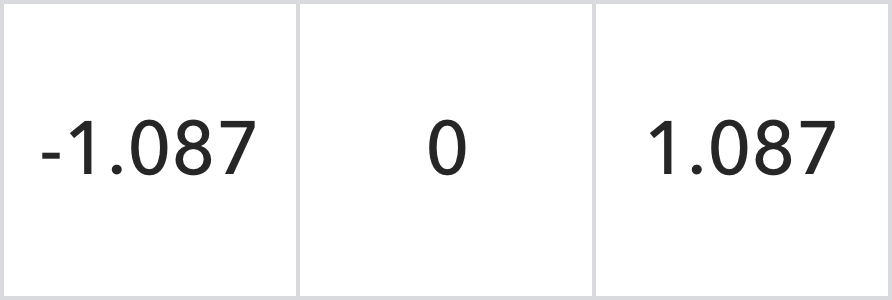More than 1 year has passed since last update.

Gaussian Blur

Posted at 2022-05-27

1. Gaussian Blur (一) ―― 基礎アルゴリズムとその実装

1.1 基礎知識

ガウシアンぼかし(Gaussian Blur)は、Gaussian Smoothingとも呼ばれ、画像をぼかすための典型的なアルゴリズムです。ガウシアンぼかしは、簡単に言うと、画像全体を加重平均する処理で、各画素値は自身とフィールド内の他の画素値の加重平均で得られます。

ガウシアンぼかしのアルゴリズムに入る前に、畳み込み(Convolution)演算を理解する必要があります。ここでは、行列の畳み込み演算プロセスを簡単に説明します。具体的な畳み込み演算については、関連資料を調べてください。

処理する行列があります。

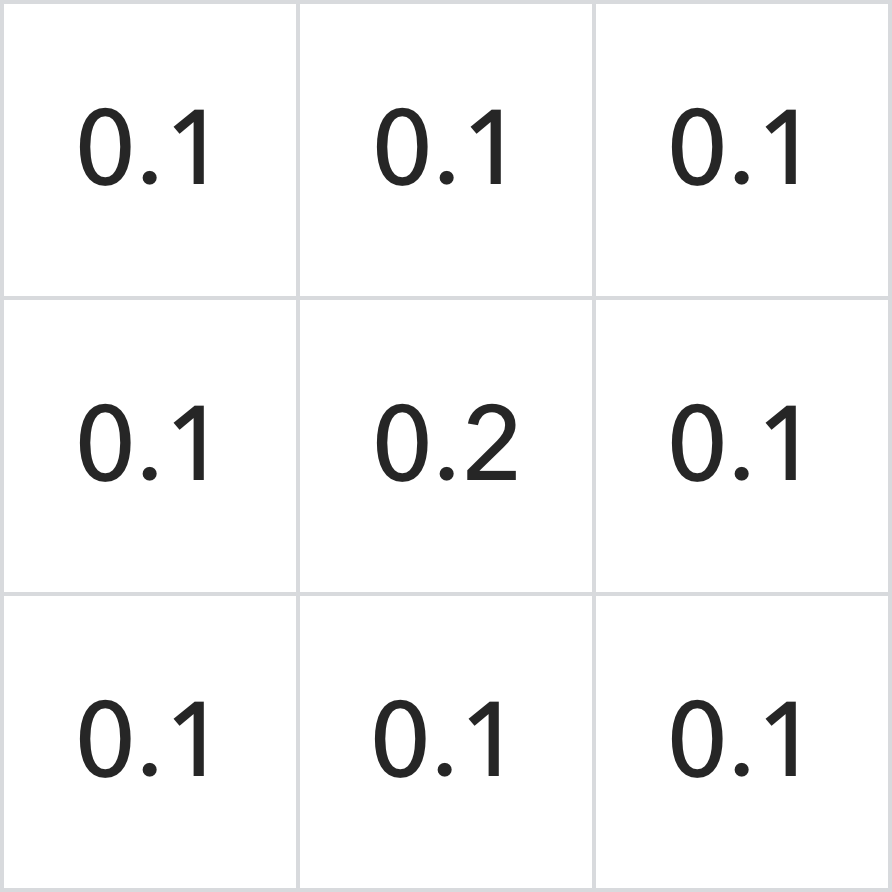
この行列が3*3の畳み込みカーネルを用いて処理されると仮定すると、このカーネルは次のようになります。

まず、畳み込みカーネルを180°反転し、元の畳み込みカーネルと同じ結果を得ます。次に、畳み込みカーネルの中心を処理対象の行列の対応する要素、例えば左上の最初の要素に合わせ、要素のないところには0を加え、対応する要素を掛け合わせて次の結果を得ます。

00.1+00.1+00.1+00.1+00.1+10.2+20.1+00.1+50.1+60.1=1.5

畳み込み演算後の最初の要素の値は1.5です。同様に、行列の他の値も最終結果まで処理します。

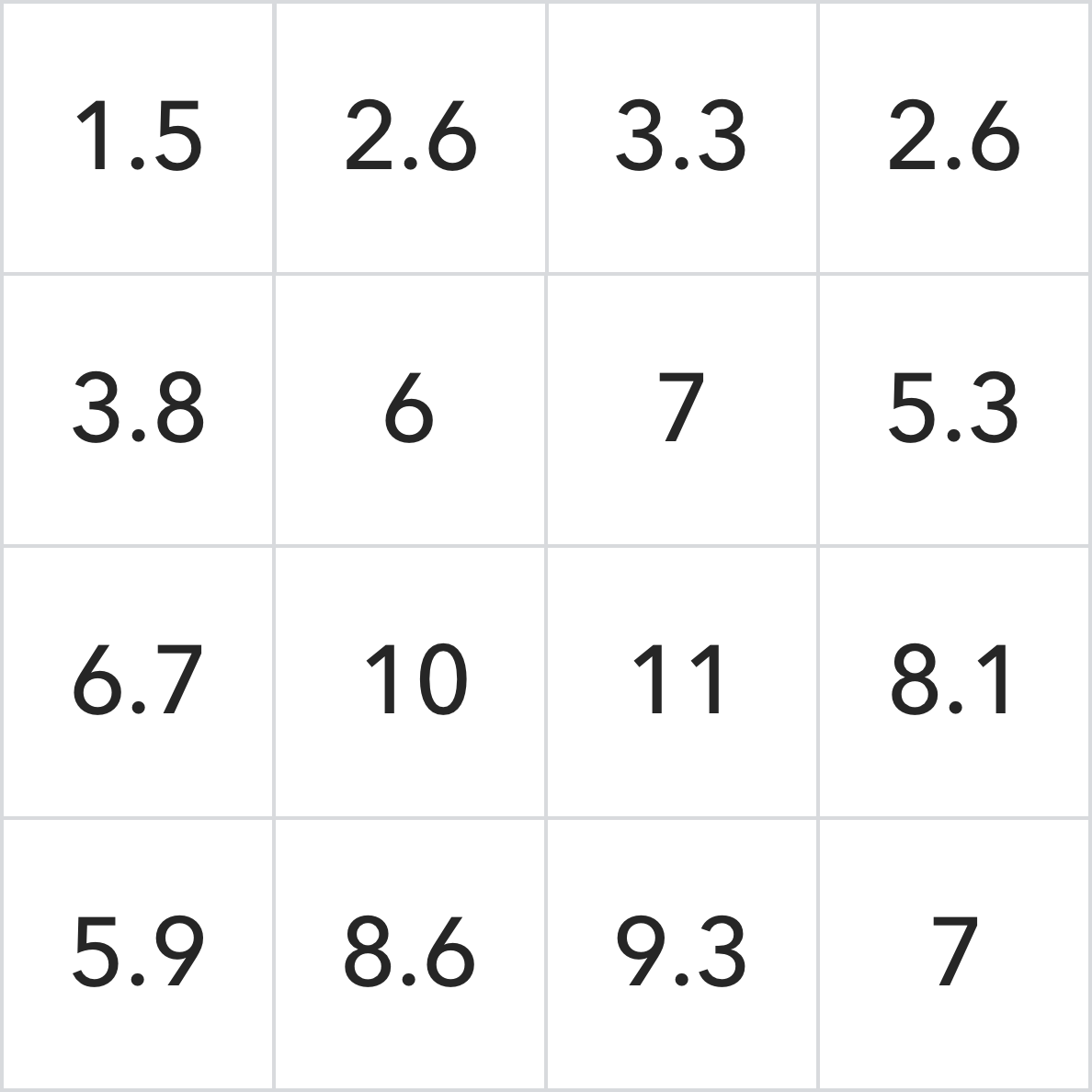
これは、SWA（Sliding Window Algorithm）の応用で、簡単な行列の畳み込み演算プロセスです。

ガウシアンぼかしはこのような畳み込み演算を利用したもので、畳み込みカーネルの計算がガウシアン分布関数を適用していることから「ガウシアン」ぼかしと呼ばれています。

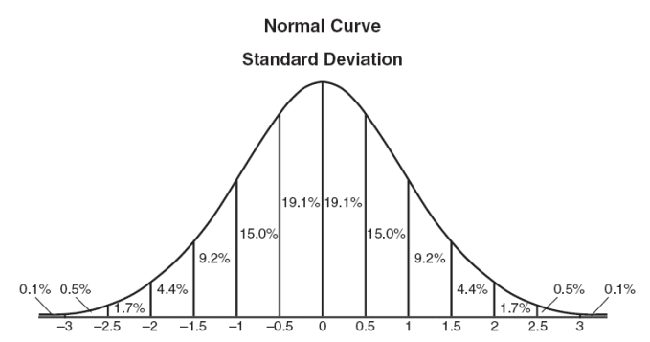
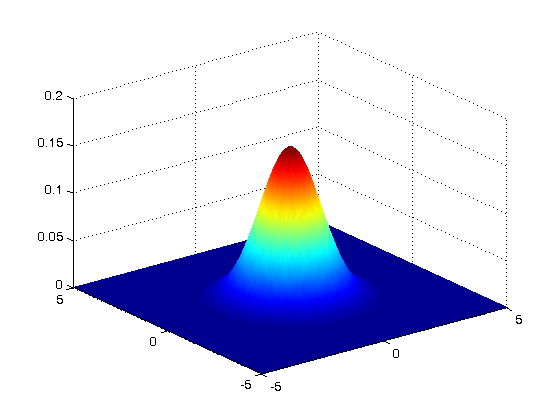
(一次元ガウシアン正規分布の密度関数）

(一次元ガウシアン正規分布の密度関数グラフ）。

さらに、2次元のガウシアン分布の式は次のように求められます。

これを正規化すると、次のようになります。

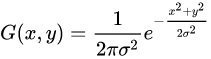
ここで、uは行、vは列を表し、u, v∈｛-ω, -ω+1, .........｝とします。ω-1, ω}

Sは正規化定数。

概略図は次のようになります。

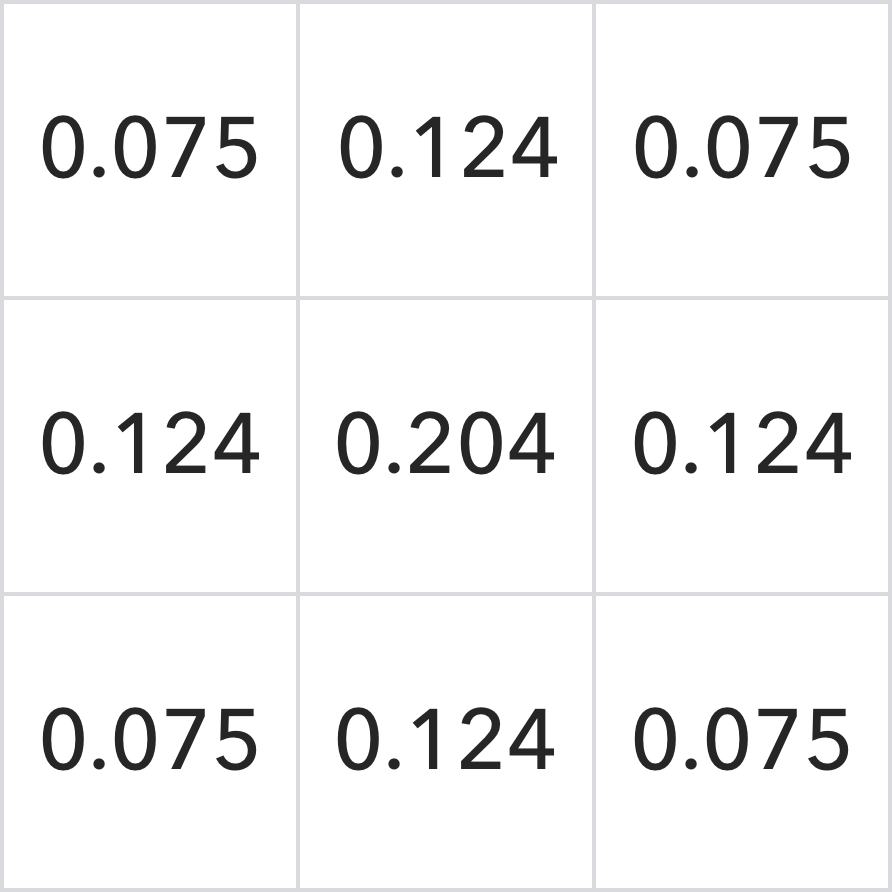
3×3の畳み込みカーネルの場合、その個々の位置の相対座標は次のように表すことができます。

式に代入して演算すると、正規化された3*3ガウシアン畳み込みカーネルが得られます。

画像に対して、ガウシアン畳み込みカーネルを用いて全画素を畳み込み演算します。最終的に得られる画像は、画像がぼかされたように見えるので、ガウシアンぼかしと呼ばれています。

出力画像をY、入力画像をXとし、i行j列のデータをX（i,j）、Y（i,j）とすると、サイズが（2ω+1）*（2ω+1）、標準偏差がσのガウシアンカーネルを用いた計算後の結果は、次のようになります。

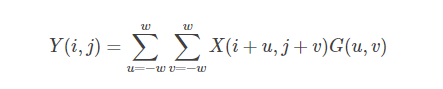
この式に従って、ガウシアンカーネルの中心を入力画像の位置(i,j)に置き、ガウシアンカーネルの各値と入力画像の対応する位置の値を掛け合わせて、（2ω+1）（2ω+1）回の乗算計算を行い、（2ω+1）（2ω+1）-1回の加算計算を行って、時間複雑度はO（ω^2）である。

また、サイズ10241024の画像に対して、サイズ3333の畳み込みカーネルを使って画像全体に1回のぼかし処理を行うには、1024102433*33≒11億4000万回のマッピングリードが必要となり、非常に時間がかかるのは間違いない。

1.2 Unityの実装

上記のアルゴリズムを元に、Unityで実装すると以下のようになります。

Shaderを作成し、 2 次元ガウシアンカーネルの計算式を実装します。

float gauss(float x, float y, float sigma)
{
	return  1.0f / (2.0f * PI * sigma * sigma) * exp(-(x * x + y * y) / (2.0f * sigma * sigma));
}

頂点シェーダは UnityCG.cginc に実装された vert_img 関数を選択し、その主な機能は、頂点をモデル空間からクロップ空間へ変換することです。

v2f_img vert_img( appdata_img v )
{
    v2f_img o;
    UNITY_INITIALIZE_OUTPUT(v2f_img, o);
    UNITY_SETUP_INSTANCE_ID(v);
    UNITY_INITIALIZE_VERTEX_OUTPUT_STEREO(o);
    o.pos = UnityObjectToClipPos (v.vertex);
    o.uv = v.texcoord;
    return o;
}

ガウシアンカーネルのサイズを設定します。

#ifdef MEDIUM_KERNEL
#define KERNEL_SIZE 35
#elif BIG_KERNEL
#define KERNEL_SIZE 127
#else
#define KERNEL_SIZE 7
#endif

各ピクセルとそのフィールドのピクセルに重みをつけるフラグメントシェーダを実装します。重みは上記のgauss関数によって得られます。

float4 frag(v2f_img i) : COLOR
{
	float4 o = 0;
	float sum = 0;
	float2 uvOffset;
	float weight;
	for (int x = -KERNEL_SIZE / 2; x <= KERNEL_SIZE / 2; ++x)
		for (int y = -KERNEL_SIZE / 2; y <= KERNEL_SIZE / 2; ++y)
		{
            //オフセットを計算する
			uvOffset = i.uv;
			uvOffset.x += x * _MainTex_TexelSize.x;
			uvOffset.y += y * _MainTex_TexelSize.y;
            //重みを確認する
			weight = gauss(x, y, _Sigma);
			o += tex2D(_MainTex, uvOffset) * weight;
			sum += weight;
		}
	o *= (1.0f / sum);
	return o;
}

以下のような結果が得られます。

原画像

(7*7のガウシアンカーネルを使用したもの)

(35*35のガウシアンカーネルを使用したもの)

DEMOリンク

2. Gaussian Blur（二）―― 2段階の1次元演算アルゴリズムとその実装

2.1 基礎知識

2次元ガウシアン関数を用いた畳み込みカーネルによる画像のぼかし処理は，リアルタイム計算を行うゲームに適用するとオーバーヘッドが大きくなります。加速を最適化し、テクスチャ読み取り操作と算術操作の数を減らすために、いくつかの方法を検討する必要があります。最適化は、2次元ガウシアン分布関数の分離可能な性質を利用することによって実行できます。

2次元ガウシアン分布関数の分離可能性とは、2次元ガウシアン関数を同じ1次元ガウシアン関数に分解して2回処理しても、どちらも等価であり、得られる結果は同じだが処理時間が大幅に短縮されることを意味します。数学的な証明式は以下の通りです。

とすると、

ガウシアンカーネル行列を、行ベクトルと列ベクトルを掛けた正規化定数として書き直します。

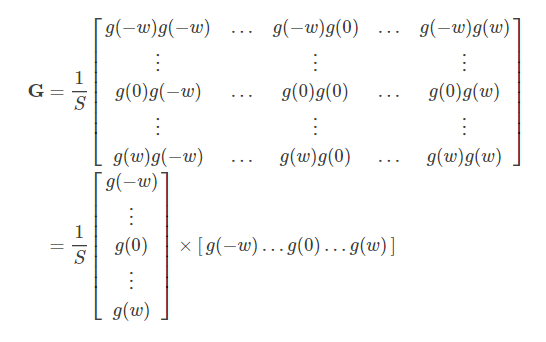
このときの正規化定数Sは、2つの1次元ガウシアンカーネルの正規化係数の逆数乗算に分割できます。

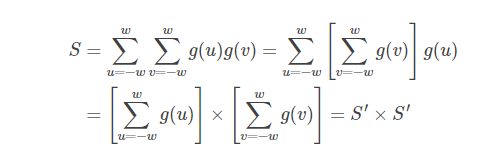
したがって、Gを2つのベクトルの積に分割することもできます。

この中には、

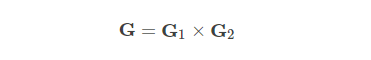
したがって、ガウシアンぼかした画像Yは次のように表すこともできます。

上記の式は、最初に1次元ガウシアンカーネルと入力画像Xを使用して水平畳み込み演算を実行し、中間結果Zを取得し、次に1次元ガウシアンカーネルと中間結果を使用して垂直畳み込み演算を実行することを示しています。結果Zを使用して、最終結果Yを取得します。

この方法でピクセルのぼかし効果を計算するには、（4ω+ 2）乗算演算と4ω加算演算が必要で、時間計算量はO（ω）であることがわかります。

1024 * 1024サイズの画像の場合、33 * 33の畳み込みカーネルを使用して画像全体にぼかし操作を実行するには、1024 * 1024 332≈6.9kwのテクスチャ読み取りを実行する必要があります。これは2次元ガウシアン畳み込みカーネルを使用した直接処理と比較して大幅に低下します。

2.2 Unityの実装

上記のアルゴリズムに従って、Unityで実装します。

まず、1次元ガウシアンカーネル計算式を実装します。

float gauss(float x, float sigma)
{
	return  1.0f / (sqrt(2.0f * PI) * sigma) * exp(-(x * x) / (2.0f * sigma * sigma));
}

1次元ぼかしアルゴリズムを実装します。

float4 GaussianBlur(pixel_info pinfo, float sigma, float2 dir)
{
	float4 o = 0;
	float sum = 0;
	float2 uvOffset;
	float weight;

	for (int kernelStep = -KERNEL_SIZE / 2; kernelStep <= KERNEL_SIZE / 2; ++kernelStep)
	{
		uvOffset = pinfo.uv;
		uvOffset.x += ((kernelStep)* pinfo.texelSize.x) * dir.x;
		uvOffset.y += ((kernelStep)* pinfo.texelSize.y) * dir.y;
		weight = gauss(kernelStep, sigma);
		o += tex2D(pinfo.tex, uvOffset) * weight;
		sum += weight;
	}
	o *= (1.0f / sum);
	return o;
}

最初のpassでの水平方向の1次元ぼかしを実行する：

struct pixel_info
{
	sampler2D tex;
	float2 uv;
	float4 texelSize;
};

float4 frag_horizontal(v2f_img i) : COLOR
{
	pixel_info pinfo;
	pinfo.tex = _MainTex;
	pinfo.uv = i.uv;
	pinfo.texelSize = _MainTex_TexelSize;
	return GaussianBlur(pinfo, _Sigma, float2(1,0));
}

Pass
{
	CGPROGRAM
	#pragma target 3.0
	#pragma vertex vert_img
	#pragma fragment frag_horizontal
	ENDCG
}

Unityの内蔵関数GrabPass{}を使用して、最初のpassの実行後に画面イメージをキャプチャします。この関数は、デフォルトで_GrabTextureという名前の変数に画像を保存し、次に垂直方向のぼかしを実現します。

float4 frag_vertical(v2f_img i) : COLOR
{
	pixel_info pinfo;
	pinfo.tex = _GrabTexture;
	pinfo.uv = i.uv;
	pinfo.texelSize = _GrabTexture_TexelSize;
	return GaussianBlur(pinfo, _Sigma, float2(0,1));
}
uniform sampler2D _GrabTexture;
uniform float4 _GrabTexture_TexelSize;

GrabPass {}関数によって取得された画像のUV座標は通常の画像と一致しないため、ぼかしアルゴリズム後の結果が反転しないようにUV座標を処理する必要があります。したがって、頂点シェーダーは次のように実装されます。

v2f_img vert_img_grab(appdata_img v)
{
	v2f_img o;
	UNITY_INITIALIZE_OUTPUT(v2f_img, o);
	UNITY_SETUP_INSTANCE_ID(v);
	UNITY_INITIALIZE_VERTEX_OUTPUT_STEREO(o);
	o.pos = UnityObjectToClipPos(v.vertex);
	o.uv = half2(v.vertex.x, 1-v.vertex.y);
	return o;
}

垂直ぼかしを実装するpass

GrabPass{}

Pass
{
	CGPROGRAM
	#pragma target 3.0
	#pragma vertex vert_img_grab
	#pragma fragment frag_vertical
	ENDCG

このように、ぼかし処理を行うには、2つのパスを使用する必要があって、結果として2つのDrawCallが必要となり、これはパフォーマンスに影響を与える重要な要素です。

ここでの実装では、比較的に時間がかかるGrabPass{}関数を使用します。OnRenderImage()関数で2つのblitを使用して、それぞれ水平操作と垂直操作を実行することを検討してください。

効果は次のとおりです。

（35 * 35のガウシアンカーネルを使用した）

3. ガウシアンぼかし(三)-線形サンプリングを使用したアルゴリズムと実装

3.1 基礎知識

ガウシアン分布関数の特性を利用することで、テクスチャの読み取りと算術演算の数を減らすことに成功しました。GPUを活用することで、さらなる高速化が可能です。これまでのアルゴリズムでは、1回のテクスチャ読み取りで1ピクセルの情報しか得られないことを前提としていましたが、GPUの場合は必ずしもそうとは限りません。画像の読み取りにバイリニア補間サンプリング（Bilinear Sampling）が有効になっている場合、GPUは複数のピクセル情報を一度に読み取ることができます。バイリニア補間を使用しても、GPUへ追加の負担をかけません。

バイリニア補間サンプリングについて、簡単に紹介します：

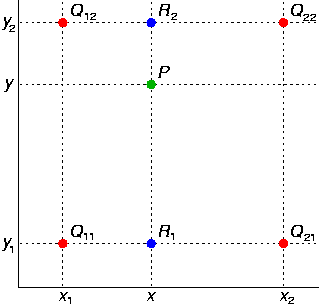
（バイリニア補間の概略図）

図に示すように、最初にx方向に2つの単線形補間を取得して、2つの一時点R1（x、y1）とR2（x、y2）を取得し、次にy方向に1つの単線形補間を計算してP（x、 y）を得ます。

つまり、テクスチャピクセルを読み取る場合、テクセルの中心にあるテクスチャを読み取らないように選択し、読み取るのに適した位置を選択することで、GPUバイリニア補間によって2つのピクセルの情報を取得できるようになります。

離散サンプリングと同じ効果を維持するには、位置の重みが2つのテクセルの重みの合計に等しくなるように、読み取り座標を調整する必要があります。つまり、簡略化されたガウシアンカーネルの重みと位置は次の要件を満たす必要があります：

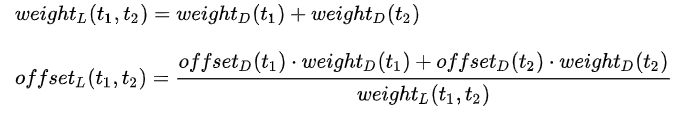
たとえば、5*5のガウシアンカーネルの場合、2つの1次元ガウシアンカーネルに分割します。ここで、横方向のガウシアンカーネルは次のようになります。

位置：

重み：

次のように置き換えることができます：

位置：

重み：

ハードウェア実装による丸め誤差を無視すると、線形サンプリングによって得られた結果は、離散サンプリングによって得られた結果と同じになります。このようにして、（2ω+ 1）（2ω+ 1）のガウシアンカーネルは（ω+ 1）（ω+ 1）のガウシアンカーネルに簡略化されます。ピクセルをぼかすには、（2ω+ 2）回の乗算、2ω回の加算、時間計算量はO（ω）になります。

1024 * 1024サイズの画像の場合、33 * 33サイズの畳み込みカーネルを使用して画像全体にぼかし操作を実行する場合は、1024 * 1024 172≈3.56kwのテクスチャ読み取りを実行する必要があります。以前の離散サンプリングより、テクスチャ読み取りの数が大幅に減少しました。

3.2 Unityの実装

上記のアルゴリズムに従って、Unityで実装します。

操作を容易にするために、選択したサンプリングポイントは直接中間点として設定されるため、得られた結果には前の結果と一定の誤差があります。基本的なプロセスは前の方法と同様であり、ぼかしアルゴリズムが実装されています。この時点では、ガウシアンカーネルを1つずつ読み取る必要はなく、ステップサイズを2に変更します。

float4 GaussianBlurLinearSampling(pixel_info pinfo, float sigma, float2 dir)
{
	float4 o = 0;
	float sum = 0;
	float2 uvOffset;
	float weight;

	for (int kernelStep = -KERNEL_SIZE / 2; kernelStep <= KERNEL_SIZE / 2; kernelStep += 2)
	{
		uvOffset = pinfo.uv;
		uvOffset.x += ((kernelStep + 0.5f) * pinfo.texelSize.x) * dir.x;
		uvOffset.y += ((kernelStep + 0.5f) * pinfo.texelSize.y) * dir.y;
		weight = gauss(kernelStep, sigma) + gauss(kernelStep + 1, sigma);
		o += tex2D(pinfo.tex, uvOffset) * weight;
		sum += weight;
	}
	o *= (1.0f / sum);
	return o;
}

効果は次のとおりです。

（35 * 35のガウシアンカーネルを使用）

3.3 まとめ

ガウシアンぼかしアルゴリズムによって実装されたぼかし効果の品質は良好ですが、パフォーマンスの点からみると思いどおりになりません。畳み込みアルゴリズムでは画像のサンプリング回数が多過ぎて、線形サンプリングアルゴリズムでは、2回のパスが必要のためDrawCallの数を2倍にしました。これらはすべて、ガウシアンぼかしアルゴリズムの実際のアプリケーションパフォーマンスに影響します。これにより、開発者はぼかしアルゴリズムを最適化し、ガウシアンぼかし効果の品質を可能な限り達成しながら、実際のニーズを満たすようにパフォーマンスを向上させることができます。次の章では、画像ぼかしアルゴリズムのいくつかの改善されたアルゴリズムを学習します。

DEMOリンク：https://github.com/UWA-MakeItSimple/Course-PostProcessingEffect/blob/main/Assets/Shaders/Blur/GaussianBlur/FirstDimensionGaussianBlur.shader

参考資料：

Gaussian Kernel Calculator：http://dev.theomader.com/gaussian-kernel-calculator/

デモアドレス：https://github.com/VestLee/VestImageEffect

UWA Technologyは、モバイル/VRなど様々なゲーム開発者向け、パフォーマンス分析と最適化ソリューション及びコンサルティングサービスを提供している会社でございます。

今なら、UWA GOTローカルツールが15日間に無償試用できます！！
よければ、ぜひ！

UWA公式サイト：https://jp.uwa4d.com
UWA GOT OnlineレポートDemo：https://jp.uwa4d.com/u/got/demo.html
UWA公式ブログ：https://blog.jp.uwa4d.com

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up