試しに、FORTRANで一質点の時刻歴応答解析を行うコードを書いてみようと思います
運動方程式
古典力学分野で解析系の研究をしていた人にとっては、馴染みの深い式かと思います。
m \frac{d^2 x}{dt^2} + c \frac{dx}{dt} + kx = -m\frac{d^2 x_0}{dt^2}
という形が一般的でしょうか。
(mは質量、cは粘性減衰定数、kはバネ剛性、右辺は地動加速度による外力項)
これを、
- 一質点モデル、バネは弾性
- 入力地震波は阪神大震災の観測波(JMA Kobe NS)
- ニューマークのβ法は平均加速度法(β=1/4)
で、解いてみようかと思います。
また、減衰力を合わせた応答スペクトルを用いて、解析の妥当性を確認します。
FORTRANでコードを書く
早速、コードを書いてみようと思います。
まずは文字の定義から。
program equationOfMotion
implicit none
!---文字の定義------
integer :: i, n, step
real(8) :: ydd_EqNS(20000), ydd_EqEW(20000), ydd_EqUD(20000) !地震波(gal)
real(8) :: y(20000), yd(20000), ydd(20000), time(20000) !変位(m)、速度(m/s)、加速度(m/s/s)、時間(s)
real(8) :: beta, dt, omega, T, h, m, k, c, pi, delta_p,epsilon, delta_y
implicit none忘れずに書きましょうね。
平均加速度法なのでβ=1/4、減衰は5%で剛性比例型減衰としました。
ちなみに、一次固有周期は1.0sになるよう、質量とバネ剛性を決めました。
beta = 0.25 !β法(平均加速度法なので1/4)
h = 0.05 !減衰定数(5%の減衰を与える)
c = 2.0 * h * k / omega !粘性係数(剛性比例型)
解析部分は以下のように記述しています。次ステップの変位を仮定して一度運動方程式を解き、その後、誤差が一定の値以下になるまで、収斂計算をしていきます。収斂計算の誤差はε以下として、
\epsilon = 1.0 \times 10.0^{-5.0}
と設定しました。
!---次ステップの値を求める----------
do n = 1, step, 1
y(n+1) = y(n) !変位を仮定
ydd(n+1) = (y(n+1) - y(n)) / (beta * dt**2) - yd(n) / (beta * dt) - ydd(n) * (1.0 / (2.0 * beta) - 1.0) !加速度を求める
yd(n+1) = yd(n) + 0.50 * (ydd(n) + ydd(n+1)) * dt !速度を求める
!---収れん判定(収れんしていない場合にはループの計算を続ける)---
do
delta_p = (-1.0) * m * ydd_EqNS(n+1) * 0.01 - (m*ydd(n+1) + c*yd(n+1) + k*y(n+1)) !不釣合力を計算
if (abs(delta_p).lt.epsilon) exit
delta_y = delta_p / (k + m / (beta * dt**2) + c /(2.0*beta*dt))
y(n+1) = y(n+1) + delta_y !変位修正
ydd(n+1) = (y(n+1) - y(n)) / (beta * dt**2) - yd(n) / (beta * dt) - ydd(n) * (1.0 / (2.0 * beta) - 1.0) !加速度を求める
yd(n+1) = yd(n) + 0.50 * (ydd(n) + ydd(n+1)) * dt !速度を求める
end do
解析結果
今回作ったモデルでの解析結果を以下に記します。
FORTRANでの解析結果
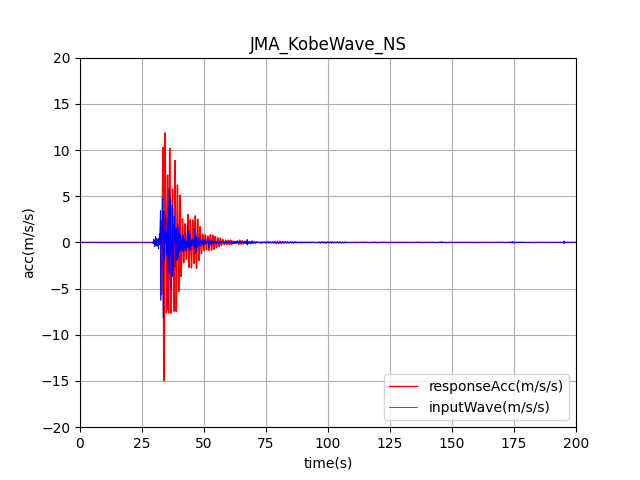
青線が入力地震動、赤線が応答値です。
最大応答加速度(絶対値):14.967(m/s/s)
となっており、かなり揺られていることがわかります。
加速度応答スペクトル

今回は一次固有周期1.0sなので、グラフからは 約15(m/s/s) と読み取れます。
これより解析モデルの妥当性が確認できました。
久しぶりにFORTRANでコードを書いたので、割と手こずりましたが、解析できるまでコーディングできたので良かったです。
