はじめに

世の中には多くのネットワーク構造が溢れています．

ネットワーク構造を理解することは世の中の構造を理解することにつながります．

かのGoogleもWWWのネットワーク構造に着目し，重要なホームページを評価するための指標としてPageRankを利用することでここまでの富を成し，世の中を支配するに至りました．

そこで今回はネットワーク解析の中心性について有名な指標をいくつか紹介したいと思います．

中心性

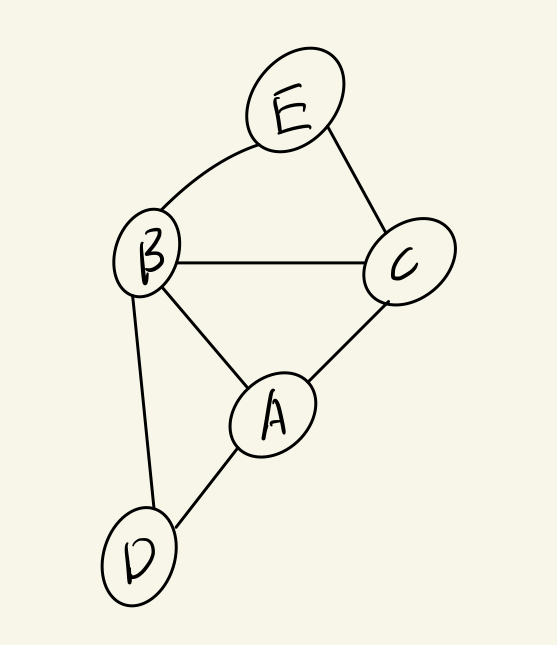
中心性の例として仮想のSNSによる相互フォローを考えます．
ノードはユーザを表し，リンクはそれぞれのユーザがお互いに相互フォローの場合にリンクが貼られます．

$n$はノードの数を，$d_{（i, j)}$はノード$i$とノード$j$の最短経路を，$k_i$はノードiの次数(ノードに繋がれているリンクの数)を表します．

次数中心性は「ノードに接続されるリンクの数」になります．

DegreeCentrality_i = \frac{k_i}{n-1}

上記のグラフでは $B=4$でありになり，単純に相互フォローの人間が多い人が高くなります．
計算時間はリンクを数えるだけなのでそこまで必要なくすぐに計算が可能です．

近接中心性は「全体のノードとの最短経路がどのくらい近いか」の指標になります．

ClosenessCentrality_i = \frac{n-1}{\Sigma_{j=1}^{n-1}d_{(i, j)}}

対象のノードから全ノードへの最短経路の和の逆数となります．
SNSの例だと「コミュニティ内の全員と最短で知り合える人」となり，$B=1$となり最大となります．

媒介中心性は「ネットワーク全体の最短経路の中心」となります．

BetweennessCentrality_i = \sum_{j\neq k \neq i}\frac{d_{(j,k)(i)}}{d_{(j,k)}}

$d_{(j, k)(i)}$は$j$と$k$を通る最短経路のうち$i$を通る最短経路の数を表し，$d_{(j,k)}$は$j$と$k$の最短経路になります．
これにより，媒介中心性とは全ノードの組み合わせのうち対象のノードを通る経路の割合を表します．

SNSの例だと「コミュニティの人と人の繋がりの中心人物」となり，Bが最大となります．

その他の中心性として

などが挙げられます．

かなり奥が深く場合により使用する値が変わるため調べてみると面白いです．

中心性の主要なもの3つをまとめましたが，ネットワーク解析における指標にはさまざまなものがあり，場合によって使用する場面が変わるため，色々な指標を知っているとものを考える角度が変わるかもしれません．

また，近年はネットワークにニューラルネットを適応させてGraph Convolutional Networks(GCN)も注目を集めているため，GCN周りのサーベイをしてみると新たなる分析ができるかもしれません．