Goldstein-Price FunctionのLocal Minimumと戦ってみた

以前，SciPyライブラリの中にOptimizerテスト用としてRosenBrock関数があることを知ったが，Wikipediaを調べていたところ，RosenBrock以外にもいろいろベンチマーク用の関数が存在することが分かった．

一番単純な形の Sphere Function は直観的に最適解（最小値点）を求めるのは容易と予想されるが，他の関数は見るからに最適解を求めるのが難しそうなものがある．今回はこの中から"Goldstein Price Function"を取り上げてみたい．

Fig. Sphere Function

（参考図，これなら扱いは簡単ですが...）

Fig. Goldstein-Price Function

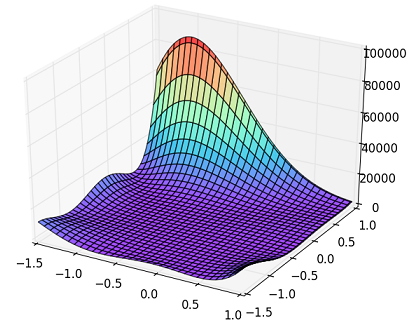
（今回は，これを扱います．）

Goldstein-Price Functionの性質

まず関数の数式は以下のようなものである．

f(x,y) = (1+(x+y+1)^2 (19 -14x+3x^2-14y+6xy+3y^2))\\
(30 + (2x -3y)^2 (18 - 32x +12x^2 +48y -36xy+27y^2)

上図の3Dプロットに示される通り，x軸，y軸の数値に対してz軸の数値が大きくなっているように関数の非線形性が大きい．この関数の最小値点（最適解）は，

f(0, -1) = 3

の通り，(x, y) = (0,-1) で z = 3 を得るが，この周囲に複数，極小点(Local Minimum)が存在する．その状況を詳しく見るために等高線図(contour図)を描いてみた．

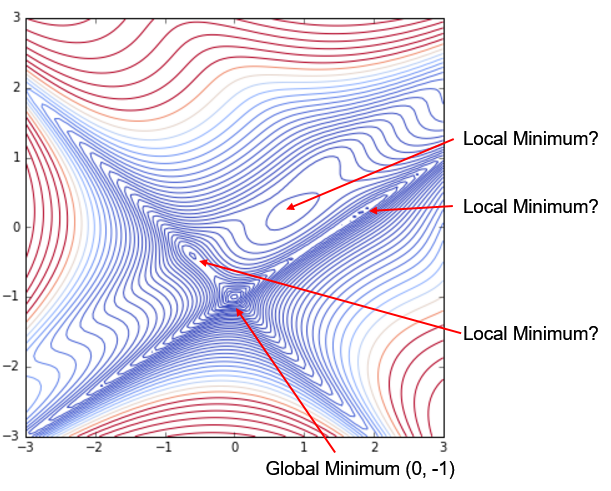
斜めの十字状に溝のような形状があり，その溝の交差ポイントがGlobal Minumumポイント (x, y) = (0, -1) である．その右上，(1, 0.2)付近にやや大きいエリアの島があり，ここはLocal Minimumを取る可能性がある．また溝形状部に小さいLocal Mimimum候補が観測される．これは，扱いが難しそうである．

TensorFlowで解く

いろいろなオプティマイザを用意しているということで，TensorFlowを使って解くことにした．コードは以下のようになる．

まずGoldstein-Price関数の定義である．関数の定義通りにコード化するが，2乗の計算は tf.square()を用いている．

def goldsteinprice_tf(x, y):
    # goal : (x, y) = (0., -1.0)
    term1 = (19. - 14. * x + 3. * x * x -14. * y + 6. * x * y + 3. * y * y)
    term2 = 1. + tf.square((x + y + 1.0)) * term1
    term3 = 18. -32. * x + 12. * x * x + 48. * y - 36. * x * y + 27. * y * y
    term4 = 30. + tf.square((2. * x - 3. * y)) * term3
    z = term2 * term4
    return z

初期値をセットして，コストとしてGoldstein-Price関数を与える．

    # set initial parameter
    x0, y0 = (0., 0.)
    x = tf.Variable(x0)
    y = tf.Variable(y0)
    loss = goldsteinprice_tf(x, y)

オプティマイザは，6種類のTensorFlow Optimizerから選べるようにした．

    lrate = 1.e-03    # 学習率
    sw = 4            # Optimizer Selection
    
    # need to check sw = [2, 5]
    if sw == 1:
        optimizer = tf.train.GradientDescentOptimizer(lrate)
    elif sw == 2:
        optimizer = tf.train.AdagradOptimizer(lrate, initial_accumulator_value=0.1)
    elif sw == 3:
        optimizer = tf.train.MomentumOptimizer(lrate, momentum=0.0)
    elif sw == 4:
        optimizer = tf.train.AdamOptimizer(lrate)
    elif sw == 5:
        optimizer = tf.train.FtrlOptimizer(lrate)
    elif sw == 6:
        optimizer = tf.train.RMSPropOptimizer(lrate, decay=0.0)
    else:
        print('Error.')
    
    train_op = optimizer.minimize(loss)

あとは，変数を初期化してセッションを走らせるだけである．

   init = tf.initialize_all_variables()

    with tf.Session() as sess:
        sess.run(init)
        print('Training...')
        print('initial (x, y) = (%8.4f, %8.4f) : loss = %8.4f' 
            % (sess.run(x), sess.run(y), sess.run(loss)))
        
        for i in range(10001):
            train_op.run()

            if i % 100 == 0:
                loss_ = float(sess.run(loss))
                # loss_log.append(loss_)
                x_ = sess.run(x)
                y_ = sess.run(y)
            
            if i % 1000 == 0:                # echo status on screen
                print('(x, y) = (%8.4f, %8.4f) : loss = %8.4f' 
                    % (x_, y_, loss_))

        # Check trained parameter
        print('final (x, y) = (%8.4f, %8.4f) : loss = %8.4f' 
            % (sess.run(x), sess.run(y), sess.run(loss)))

選べる計算パラメータとしては，

• 初期値 (x0, y0)
• Optimizerの種類
• 学習率及びLoop処理回数
  となる．

計算例として上記リストの設定（初期値(0,0), AdamOptimizer, Loop 10,000回）の実行結果が以下のようになる．

Training...
initial (x, y) = (  0.0000,   0.0000) : loss = 600.0000
(x, y) = ( -0.0010,  -0.0010) : loss = 598.5597
(x, y) = ( -0.5198,  -0.4769) : loss =  31.8792
(x, y) = ( -0.5756,  -0.4230) : loss =  30.2262
(x, y) = ( -0.5987,  -0.4012) : loss =  30.0007
(x, y) = ( -0.6000,  -0.4000) : loss =  30.0000
(x, y) = ( -0.6000,  -0.4000) : loss =  30.0000
(x, y) = ( -0.6000,  -0.4000) : loss =  30.0000
(x, y) = ( -0.6000,  -0.4000) : loss =  30.0000
(x, y) = ( -0.6000,  -0.4000) : loss =  30.0000
(x, y) = ( -0.6000,  -0.4000) : loss =  30.0000
(x, y) = ( -0.6000,  -0.4000) : loss =  30.0000
final (x, y) = ( -0.6000,  -0.4000) : loss =  30.0000

見事にLocal Minimum (-0.6, -0.4)に捕まっている状況である．因みに初期値をGlobal Minimumの近傍にセットして計算してみたところ，きちんとMiniumポイント(0, -1)に収束することが確認できた．

Global Optimizationの手法「焼きなまし法」

ここで一旦TensorFlowを離れて，Global Optimizationの手法「焼きなまし法」(Simulated Annealing) を試してみる．Wikipediaでの説明は次の通り．

SAアルゴリズムは、解を繰り返し求め直すにあたって、現在の解のランダムな近傍の解を求めるのだが、その際に与えられた関数の値とグローバルなパラメータ T（温度を意味する）が影響する。そして、前述の物理過程との相似によって、T（温度）の値は徐々に小さくなっていく。このため、最初はTが大きいので、解は大胆に変化するが、Tがゼロに近づくにつれて収束していく。最初は簡単に勾配を上がっていけるので、山登り法で問題となるようなローカルな極小に陥ったときの対処を考える必要がない。

すばらしいことに疑似コードも掲載されていたので，それをPythonコードに直して実行してみた．

コード主要部は以下の通り．

def sim_anneal(startState, maxIter, goalE):
    state = startState
    x_, y_ = state[0], state[1]
    e = goldsteinprice(x_, y_)
    bestState = state
    bestE = e
    for iter in range(0, maxIter):
        delta = np.random.rand(2) - 0.5
        nextState = state + delta * 1.
        nextE = goldsteinprice(nextState[0], nextState[1])
        
        if bestE > nextE:
            bestState = nextState
            bestE = nextE
            if goalE >= bestE:
                return bestState
        r = np.random.rand()
        if probability(e, nextE, temperature(10.0, iter/maxIter)) >= r:
            state = nextState
            e = nextE
        if iter % 100 ==0:
            print('iter: nextE, bestE, goalE = (%5d, %9.3f, %9.3f, %9.3f)' 
               % (iter, nextE, bestE, goalE))
            
    return bestState

計算を実行したしてみると，見事Global Munimum (0.0, -1.0)の近傍に到達している．

Fig. Parameter(x,y) Path (Simulated Annealing)

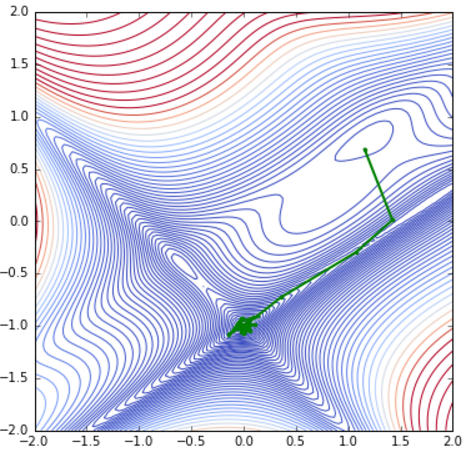
この計算でも初期値の他，いろいろな計算パラメータの選択肢がある．また，何度か計算を走らせて気づいたこととして，乱数の性質に影響を受ける点がある．乱数のseedをセットせず，何度が計算を実行すると，全く別の場所で計算を終了してしまうケースがあった．結果が読みにくいこともあり，万能な計算手法とは言えない感じである．

TensorFlowのオプティマイザでやり直し

初期値の影響を見るために，9点の初期値：
[[0., 0.], [0., 1.], [1., 0.], [1., 1.], [0., -1.], [-1., 0.], [-1., -1.], [-1., 1.], [1., -1.]] で計算を行った．

まずAdagradOptimizerを使った計算結果を以下の図に示す．

Fig. Parameter(x,y) path from 9 points (Adagrad)

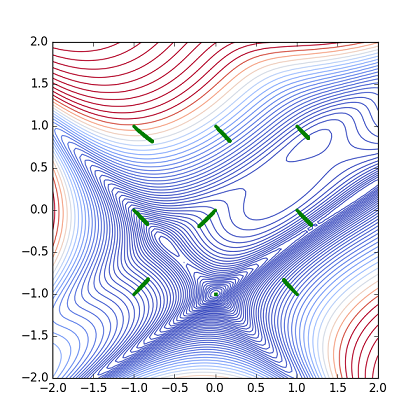
初期からGlobal Minimumにあったケースを除いて，どれも最小点に届いていない．（学習率他のパラメータを調整すれば，改善するかも知れません．）
AdamOptimizerを使った結果が下図となる．

Fig. Parameter(x,y) path from 9 points (Adam)

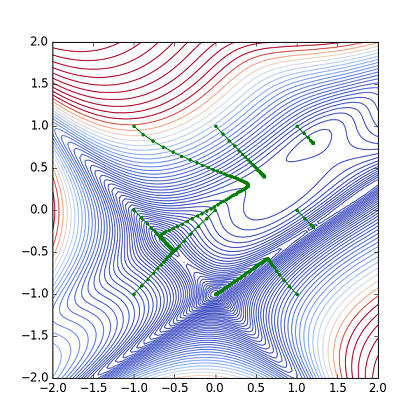
ここでは２つのケースで最小点に達しているが，１つは初期値が最小点であったので除外すると，(x0, y0) = (1.0, -1.0) のケースもうまくいっている．

以上の状況から，最後に初期値設定に乱数を用いて試してみた．通常，ニューラルネットの学習では，重み係数(weights)の初期化に乱数を用いるが，その目的は「ネットの対称性を排除することにより学習の進み具合を促進する」ことにある．今回はLocal Minimumに落ちる可能性を考慮して広くパラメータを振るために乱数の初期化を行うということで，少し意味合いが異なる．

    num_jobs = 10

    with tf.Session() as sess:
        for job in range(num_jobs):
            init_param = tf.Variable(tf.random_uniform([2], minval=-1., maxval=1.))
            x = tf.slice(init_param, [0], [1])
            y = tf.slice(init_param, [1], [1])

            loss = goldsteinprice_tf(x, y)
 （後略）

上記のようにtf.random_uniform() で -1.0 ~ 1.0 の乱数を発生して初期値として用いた．計算結果は以下のようになった．

Fig. Parameter(x,y) path from random point

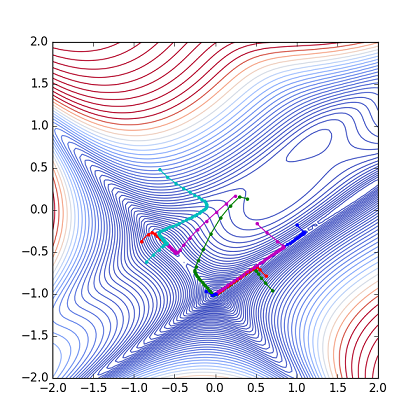
（Pathの色を分けてみました．）

9点初期値の結果からもう少し悲観的であったが，かなりの確率でGlobal Minumumの(0, -1) に到達している．30%以上の確率でGolobal Minimumを探せている．

今回，実用的な目的はなくGoldestein-Price関数と「戦って」みたが，最適点探索の難しさがいろいろ分かってきた．初期値に乱数を用いることでLocal Minimumの問題はある程度回避できるが，その乱数の範囲はどうするの？ということに対してまだ汎用的な答えがないように思われる．

但し，実際の分類問題において学習データが入力される状況を想定すると，学習データ自体に誤差がのっており，かつ確率的勾配降下法を用いることでLocal Minimumに捕らわれない状況もあるのでは，と考えている．（もちろん，時間をかけられる状況ではいろいろな初期値を試すことは非常に有用と思います．）

参考文献 (web site)

• Test functions for optimization (wikipedia) ... きれいな関数の図(3D plot)が掲載されています．
  https://en.wikipedia.org/wiki/Test_functions_for_optimization
• 焼きなまし法 (wikipesida)
  https://ja.wikipedia.org/wiki/%E7%84%BC%E3%81%8D%E3%81%AA%E3%81%BE%E3%81%97%E6%B3%95
• Tensorflow Document ... ver. 0.7.0 に上がっていました．(2016/2/22時点)
  https://www.tensorflow.org/
• 今一度Theanoの基本を学ぶ - Qiita
  http://qiita.com/TomokIshii/items/1f483e9d4bfeb05ae231