前回の記事「やってみたら簡単!ディープラーニング・オセロを作って自分を負かすまで強くした話(その1)」の続編です。
前回は、ディープラーニング・オセロのモデルを作って推論させるところまでを説明しました。
今回は、今回はこのモデルをiOSで動作させ、ミニマックス法やモンテカルロ木探索に組み込む方法について説明します。
前回、UIの説明をすると書きましたが、UIそのものはもともと参加していたコンテストであるリバーシチャレンジから提供されていたものを利用していたので、説明としては省略します。
前回はPython中心の記事でしたが、今回はSwift + Core ML中心の記事になります。
コードはこちらにあります。
TokyoYoshida/reversi-charenge
ミニマックス法とモンテカルロ木探索ではどうだったか?
結論から言うと、ミニマックス法は強くならず、モンテカルロ木探索は、私との勝率は半々ぐらいでした。
コンピュータが打った手の例を紹介します。
- 隅が取られちゃうよ!(ミニマックス法)

- あんまり意味なくない?(モンテカルロ木探索)

- 完全勝利しちゃったよ!(モンテカルロ木探索)

それでは、実装方法を説明します。
1.訓練したモデルをiOS用に変換する
前回保存したモデルをCore MLのモデルに変換します。
(Google Colab上で前回の続きから操作します)
!pip install -U coremltools==4.0
mlmodel = ct.converters.convert('./saved_model_reversi/my_model/',source="tensorflow")
mlmodel.save('./reversi.mlmodel')
保存したreversi.mlmodelをダウンロードしてXcodeのプロジェクトにDrag & DropすればCore MLのモデルとして動作します。
2. iOSデバイス上で推論させる
AIが実際に手を打つ時の処理について説明します。
盤面の情報をCore MLモデルの入力の形に変換し、Core MLモデルのpredictionメソッドを呼び出すことで推論させることができます。
推論結果はクロージャに渡されますが、内容は前回の記事のモデルの推論結果と同じです。
オセロのマスに対応した64の要素を持つ1次元配列で、それぞれのマスの勝率が入っています。これをデコードしてルール上ありえない手などを取り除き、最善手をAIの手とします。
func predict(_ board: [State], _ targetPlayer: State, completion: ([Float32]) -> Void) {
// Core MLのモデルを取得する
let model = try reversi()
// 画面の盤面の状態をCore MLに渡すための情報に変換する
let mlArray = boardConverter.convert(board, targetPlayer)
let inputToModel: reversiInput = reversiInput(permute_input: mlArray)
// Core MLに推論させる
if let prediction = try? model.prediction(input: inputToModel) {
let resArray = try? prediction.Identity
let results = ReversiModelDecoder.decode(resArray!)
completion(results)
}
}
ここまでがディープラーニングを使った場合の推論の実装です。
3.ミニマックス法、モンテカルロ木探索を実装する
ミニマックス法、モンテカルロ木探索法の実装は、GameKitを使いました。
GameKitは、一定の規則に基づいてゲームの規則をコーディングすると、ミニマックスやモンテカルロ木探索で推論をしてくれます。規則さえコーディングすれば、オセロだけではなく他のボードゲームも推論させることができます。
実装は次のステップを踏みます。
- プレイヤーを定義する
- 1手を定義する
- ゲームのモデル(ルールや評価)を定義する
- 推論させ、結果を受け取る
1つずつ説明します。
プレイヤーを定義する
プレイヤーの情報を扱うクラスは、GKGameModelPlayerを継承して定義します。
ここでは識別できるようにIDを渡しています。
class Player: NSObject, GKGameModelPlayer {
let playerId: Int
init(playerId: Int) {
self.playerId = playerId
}
}
1手を定義する
1手の情報をGameKitに渡すためのクラスを、GKGameModelUpdateを継承して定義します。
オセロなので1手を打ったときのマスの位置を保持します。
class Update: NSObject, GKGameModelUpdate {
// その1手の価値が入る(GameKitが使用する、こちら側からは操作しない)
var value: Int
// 1手の位置が入る(オセロの盤面を左上が0〜右下63とした場合の番号)
var position: Int
init(_ position: Int, _ value: Int) {
self.position = position
self.value = value
}
}
ゲームのモデル(ルールや評価)を定義する
ゲームのモデルは、GKGameModelを継承して定義します。
class ReversiModel: NSObject, GKGameModel {
ゲームのモデルは、GameKitが盤面を探索している途中の「ある盤面」に対して、次の情報を提供することで定義することができます。
- その盤面は、あるプレイヤーにとって勝った状態か
→func isWin(for player: GKGameModelPlayer) -> Boolに定義する - その盤面は、あるプレイヤーにとってどのような評価か
→func score(for player: GKGameModelPlayer) -> Intに定義する - その盤面で、次にプレイヤーが打てる手の候補は何か
→func gameModelUpdates(for player: GKGameModelPlayer) -> [GKGameModelUpdate]?に定義する - ある手を打つとゲームの状態はどのように変化するか
(ゲームの状態とは、盤面の変化や、プレイヤーの交代など)
→func apply(_ gameModelUpdate: GKGameModelUpdate)に定義する
推論させ、結果を受け取る
GameKitに推論させて結果を受け取ります。
パラメータを設定したらbestMoveForActivePlayerメソッドを呼ぶだけです。
ミニマックス法を使うか、モンテカルロ木探索を使うかは、最初にGKMinmaxStrategistを生成するかGKMonteCarloStrategistを生成するかが違うだけで、あとは同じゲームのモデルを渡して処理できます。
struct MinmaxReversi: ReversiStrategy {
// let strategist = GKMinmaxStrategist() // ミニマックス法を使う場合はこちらを有効にする
let strategist = GKMonteCarloStrategist() // モンテカルロ木探索を使う場合はこちらを有効にする
let gameModel = ReversiModel() // 先ほど定義したゲームのモデル
init() {
strategist.gameModel = gameModel // ゲームのルールを渡す
strategist.explorationParameter = 1 // 探索の範囲を指定するパラメータ(このあたりは好みで)
// strategist.maxLookAheadDepth = 2 // 探索の深さを指定するパラメータ(このあたりは好みで)
}
// 推論を実行する
func predict(_ board: [State], _ targetPlayer: State, completion: ([Float32]) -> Void) {
// ゲームのモデルに、現在プレイ中の盤面の状態と、手を推論したいプレイヤーを渡す
gameModel.updateState(board, targetPlayer)
var resBoard = Array(repeating: Float32(0), count: 64)
// 推論させ、結果を受け取る
if let result = strategist.bestMoveForActivePlayer() as? Update {
// 推論結果が1手だけ返ってくるので、その手を最高確率にする
// (ディープラーニングの方は複数手を予想するため、ReversiStrategyプロトコルは
// 複数手を返すようなシグニチャになっている。しかしここでは1手しか得られないので
// それを確率=1として入れる)
resBoard[result.position] = 1
}
completion(resBoard)
}
}
ここまでが、ミニマックス法とモンテカルロ木探索の実装方法の説明です。
3. なぜミニマックスはうまくいかなかったのか。
結論ファーストで書くと、
「手を予想するためのディープラーニング・モデルを評価関数に流用したのがいけなかった」
です。
今回、ミニマックス & モンテカルロ木探索の実装では、2つの場所でディープラーニングを使っています。
a. 次の手の候補を決めさせる
b. 探索中の盤面を評価させる(ミニマックス法のみ)
いずれも、使用したのは次の手を予想するためモデルです。そのため、a.の次の手の候補を決めさせることに問題はありませんでした。
しかし、b.の盤面の評価には流用できませんでした。
評価では、次のような式を使っていました。
盤面の評価 = 自プレイヤーの最善手の確率 - 敵プレイヤーの最善手の確率
つまり、自プレイヤーの確率が高ければ良い盤面だし、敵プレイヤーの確率が低ければ良い盤面と評価します。
しかしこれは間違いでした。
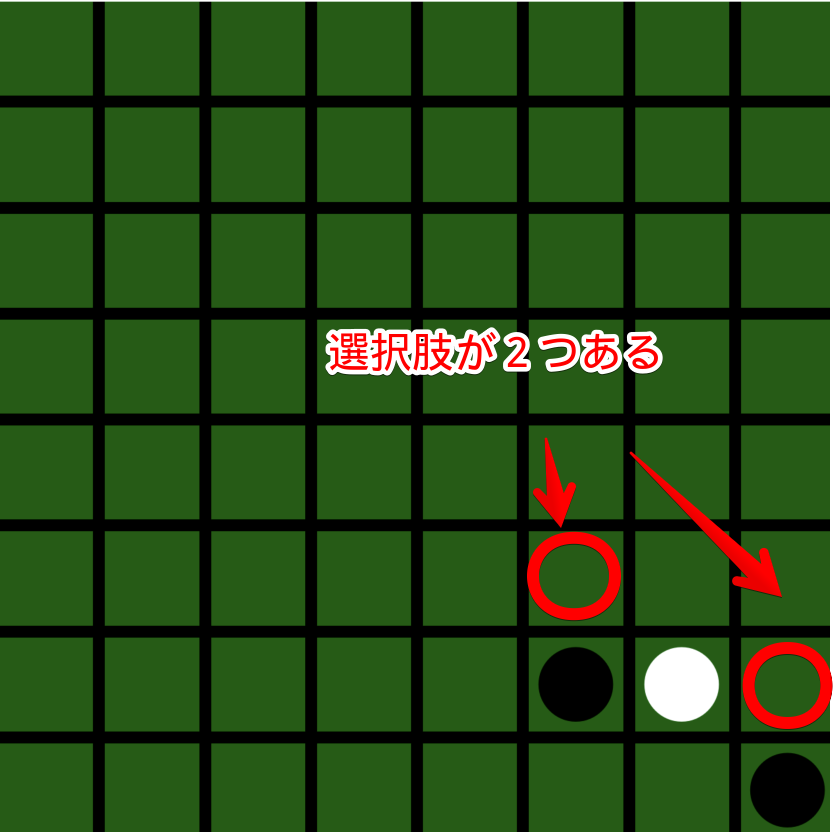
例えばこんな盤面があったとします。

白(AI)は追い込まれてますね。残り一つです。
ところがこの盤面の評価は、上の評価式だと良くなってしまいます。
上の盤面の評価値を出してみます。
白の手の確率=0.9854855
黒の手の確率=0.37575516
最終的な盤面評価=0.60973036
白の最善手の評価は0.98となっています。1が最高なのでかなり高い評価です。
なぜこうなるかというと、白が置けるのは次の場所しかないからです。
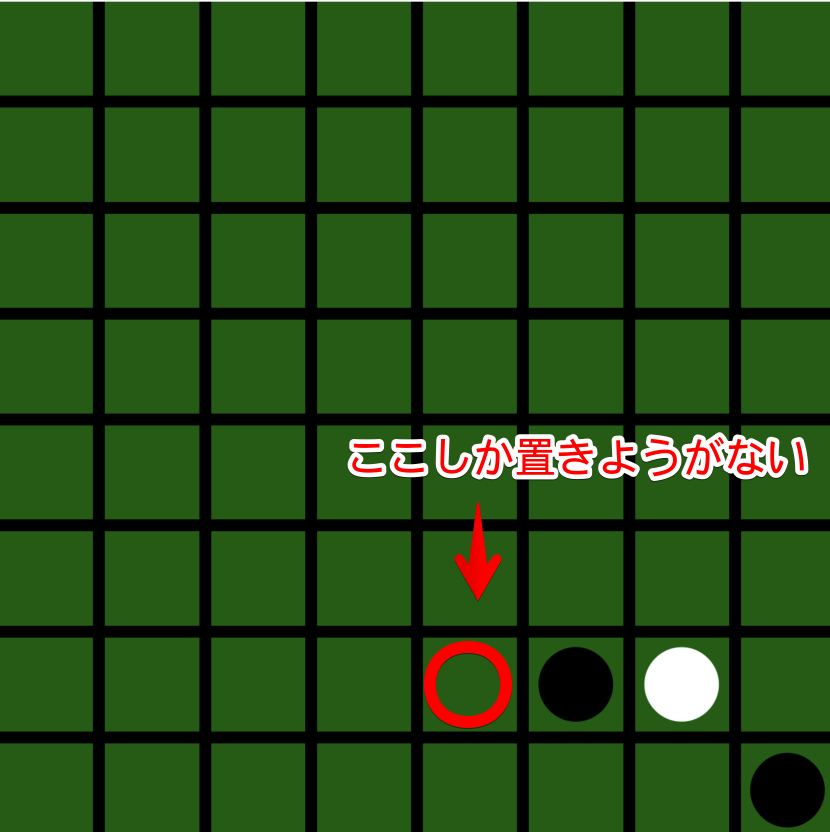
つまり、ここしか置きようがないから確率が高くなっていたわけです。
黒の最善手の確率が低いのは、選択肢が多いから割れてしまったということです。
このような評価に基づいて探索をしてしまうと、この盤面に至る手が望ましいということになってしまいます。
これがミニマックス法でうまくいかなかった理由です。
4. モンテカルロ木探索はどうだったか?
モンテカルロ木探索の場合は、勝率は半々ぐらいだったので必ずしも弱かったわけではありませんが、私の感覚ではディープラーニング版よりはかなり弱かったです。
モンテカルロ木探索では、探索の途中で盤面を評価したりせず、どちらかが勝つか引き分けるまで(投了するまで)探索するので、盤面の評価はモデルを使わずに正確に出せます。よってミニマックス法で起きたような問題は起きません。
ただ、モンテカルロ木探索は投了するまで探索するので、1手を打つのにとても時間がかかります。
ディープラーニングなら一瞬で打つ手を何秒も待っているのは退屈です。
ということで、パラメータを調整してなるべく探索範囲を狭めるようにしていました。それでも1手は4秒ぐらいかかります。
これが強くならなかった原因だと思われます。
一度だけ、探索範囲を広めるようにパラメータを調整して対戦したところ、普通に強くなっていました。
(一度だけの対戦なのでなんとも言えませんが、たぶんです)
最後に
NoteではiOS開発、AR、機械学習について書いています。
https://note.com/tokyoyoshida
Twitterでも発信しています。
https://twitter.com/jugemjugemjugem