本記事について
本記事は音響工学に関する以下参照書籍について勉強中のなか、自身の理解の定着のために記したものです。シミュレーションプログラムは参考書籍同等の部分については記載を省略しているため、本記事掲載部分のみでは動作しない場合があります。技術内容については参考書籍その他書籍やネット検索等々で調べておりますが、それを誤った解釈をして記載している可能性がありますのでご注意ください。(指摘頂けると助かります。)
参考書籍
戸上真人.「Pythonで学ぶ音源分離」インプレス.2020年
最小分散法(MVDR)のフィルタ係数
時刻$t$で扱う信号の短時間フーリエ変換によりフレーム$l$と周波数$k$で表された信号で考える。
マイクロホンアレイでの受信信号$x(l,k)$が、音源信号$s(l,k)$にステアリングベクトル$a(k)$(音源からマイクロホンアレイまでの伝達特性)をかけたものと雑音信号$n(l,k)$が加算されたモデルとする。音源分離後の推定信号$\hat{s(l,k)}$は分離フィルタ$w(k)$を用いて以下のような式で表される。
\begin{align}
\hat{s(l,k)} &= w^{H}(k)x(l,k) \\
&= w^{H}(k)(s(l,k)a(k)+n(l,k)) \\
&= s(l,k)w^{H}(k)a(k)+w^{H}(k)n(l,k)
\end{align}
音源分離後の推定信号$\hat{s(l,k)}$は、音源信号$s(l,k)$となってほしいため、以下式を満足する分離フィルタ$w(k)$とすることが理想である。
\begin{align}
w^{H}(k)a(k) &= 1 \\
w^{H}(k)n(l,k) &= 0
\end{align}
ステアリングベクトル$a(k)$はあらかじめ計算できるとするが、受信信号$x(l,k)$から直接$n(l,k)$を知ることができない。よって、上記第1式を制約条件とし、音源分離後の推定信号$\hat{s(l,k)}$が最小となる時に、雑音信号$n(l,k)$が最小になるという制約条件付き最適化問題としてフィルタ係数を決定する。
\begin{align}
制約条件&: w^{H}(k)a(k) = 1 \\
最小化&: E[|w^{H}(k)x(l,k)|^2]
\end{align}
最小化する関数をもう少し式展開すると以下のようになる。
\begin{align}
E[|w^{H}(k)x(l,k)|^2] &= E[w^{H}(k)x(l,k)x(l,k)^{H}w(k)] \\
&= w^{H}(k)E[x(l,k)x(l,k)^{H}]w(k) \\
&= w^{H}(k)R(k)w(k) \\
\end{align}
ここで、$R(k)$は入力共分散行列となる。よって、あらためて制約条件付き最適化問題を書き直すと以下のようになる。
\begin{align}
制約条件&: w^{H}(k)a(k) = 1 \\
最小化&: w^{H}(k)R(k)w(k)
\end{align}
以上を満たす分離フィルタ$w(k)$をラグランジュの未定定数法を用いて解く。ラグランジュの未定定数$\lambda$を用いてコスト関数は以下となる。
\begin{align}
F(w(k),\lambda) = w^{H}(k)R(k)w(k) + \lambda(w^{H}(k)a(k) - 1)
\end{align}
上式2変数の偏微分が0となる時の解を見つけることができればよい。
第1変数$w(k)$の偏微分より、
\begin{align}
\frac{\partial F(w(k),\lambda)}{\partial w^{*}(k)} &= R(k)w(k) + \lambda a(k) \\
&=0
\end{align}
\therefore w(k) = -\lambda R^{-1}(k)a(k)
第2変数$\lambda$の偏微分より、
\begin{align}
\frac{\partial F(w(k),\lambda)}{\partial \lambda} &= w^{H}(k)a(k) - 1 \\
&=0
\end{align}
\therefore w^{H}(k)a(k) = 1
これらの式から、$\lambda$と$w(k)$を求めればよい。まずは、$w(k)$を消去して$\lambda$を求め、$w(k)$を求める。
\begin{align}
-\lambda a^{H}(k)R^{-1}(k)a(k) = 1 \\
\lambda = \frac{-1}{a^{H}(k)R^{-1}(k)a(k)}
\end{align}
\therefore w(k) = \frac{R^{-1}(k)a(k)}{a^{H}(k)R^{-1}(k)a(k)}
最尤法によるビームフォーミング
最尤法によるビームフォーミングは、最小分散法のフィルタ係数に出てくる入力共分散行列$R(k)$の算出方法が異なるのみである。マイクロホンアレイにて音声を受信している区間と、雑音(干渉音)のみ受信していく区間が検出できる場合、雑音(干渉音)のみ受信していく区間で入力共分散行列を算出する。
線形拘束付最小分散法(LCMV)によるビームフォーミング
線形拘束付最小分散法(LCMV)は、最小分散法(MVDR)のより一般化したビームフォーミング手法に位置づけられる。最小分散法(MVDR)のフィルタ係数を導出する際に、受信信号強度が1となるようにした拘束式「$w^{H}(k)a(k) = 1$」を一般化する。
線形拘束付最小分散法(LCMV)のフィルタ係数は、拘束行列$C$と拘束応答ベクトル$h$を用いて以下の拘束条件付き最適化問題を解いて導出する。
\begin{align}
制約条件&: C^{H}w(k) = f \\
最小化&: w^{H}(k)R(k)w(k)
\end{align}
同様にラグランジュの未定定数法からフィルタ係数$w(k)$を導出すると以下のようになる。
w(k) = R^{-1}(k)C[C^{H}R^{-1}(k)C]^{-1}h
最小分散法のPythonシミュレーション確認
問題設定
こちら(ビームフォーミング(遅延和法)の理解)の記事と同様の設定とする。目的音の到来方向20度、干渉音の到来方向-60度、マイクロホンアレイ数は2個とした。
ビームフォーミング(最小分散法)の指向特性の確認
ビームフォーミングの指向特性を表示してみると以下のようになった。表示プログラムは遅延和法用いた計算処理と同様である。
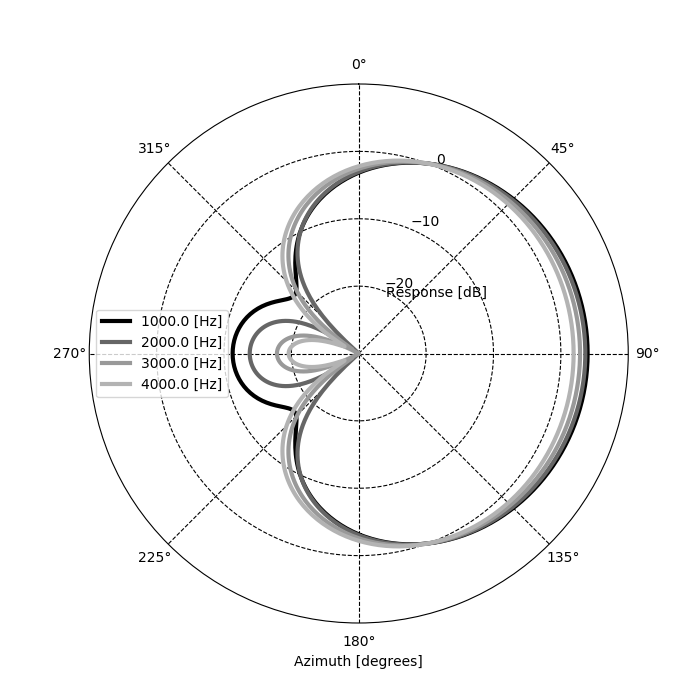
遅延和法と比較して、目的音の到来方向に指向性を絞るのではなく干渉音の到来方向(-60度)の受信を抑えるようなビームパターンとなっていることが分かる。
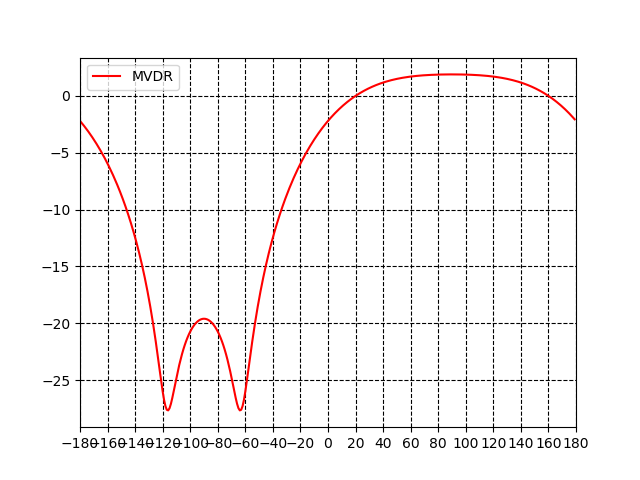
周波数4000Hzを取り出して、横軸に到来方向$\theta$[deg]縦軸に受信信号強度[dB]を表示すると以下のようである。目的音の到来方向20度で0dB、干渉音の到来方向-60度あたりで受信強度を抑えていることから、受信信号強度を変えることなく干渉音のみ抑制できるフィルタとなっていることが確認できる。
pyroomacousticsの最小分散法
pyroomacoustics の最小分散法による音源分離のシミュレーションについて簡単に記載しておく。Beamformerクラスから生成したインスタンス mics を生成する流れは遅延和法と同様だが、インスタンス生成時にFFT長$N$(第3引数)とフィルタタップ数$L_g$(第4引数)を設定する。
最小分散法のフィルタ生成は、rake_mvdr_filters にて実施される。第1引数に目的音、第2引数に干渉音、第3引数に雑音の共分散行列を設定する。
最小分散法のフィルタ係数を取得するメソッド等が無かったため、今回はpyroomacousticsとの特性比較は行えなかったが、最終行でフィルタ後信号を取得できるのでwavファイルへ出力すれば音源分離効果が確認できる。
Lg_t = 0.080 # Filter size in seconds
Lg = np.ceil(Lg_t * sample_rate) # Filter size in samples
sigma2_n = 5e-7
mics = pra.Beamformer(R, fs=room.fs, N=N, Lg=Lg) # ビームフォーマオブジェクトオブジェクト生成
room.add_microphone_array(mics) # 部屋にマイクロホンアレイ情報を設定
room.simulate(snr=SNR)
Rn = sigma2_n * np.eye(mics.Lg * mics.M)
mics.rake_mvdr_filters(room.sources[0][0:1], room.sources[1][0:1], Rn)
pra_mvdr_out = mics.process()
スペクトログラムによる音源分離性能の確認
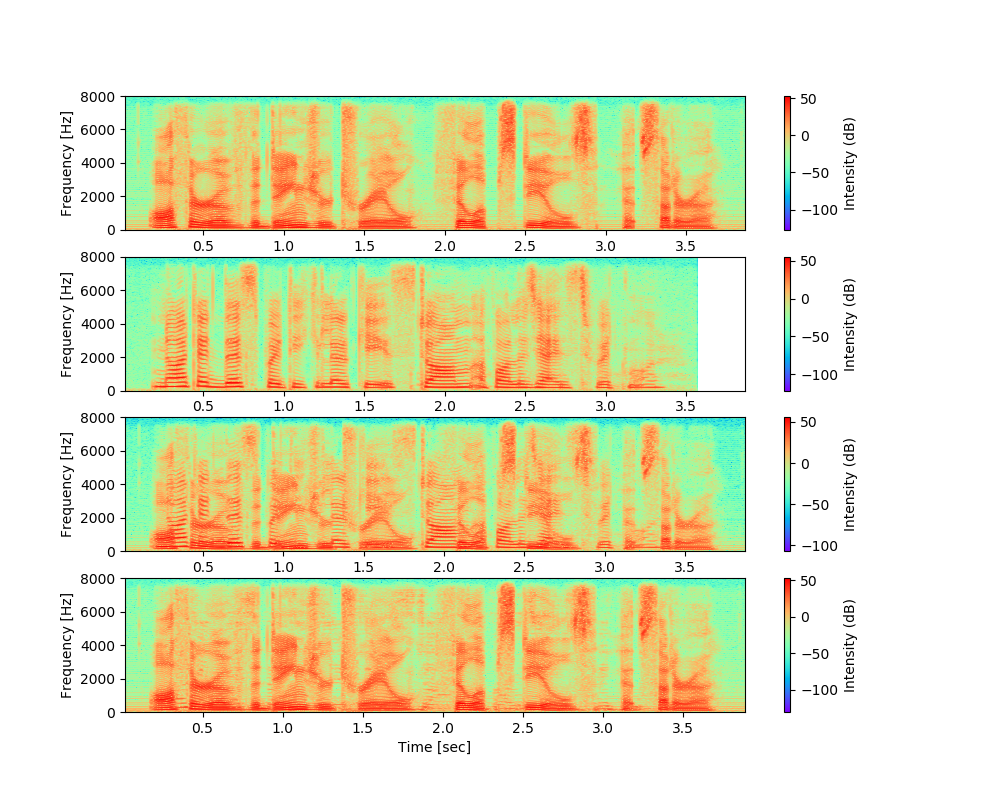
最小分散法によるビームフォーミングを用いた音源分離性能を確認した。以下図は上から目的音、干渉音、マイクロホンでの計測音(目的音と干渉音の合算)、ビームフォーミングによる分離音を示している。一番下のスペクトログラムが一番上のスペクトログラムに近ければ分離性能が良い。
今回、目的音は男性の声で主に低周波数を中心として周波数に多少広がりを持っている特徴となっている。干渉音として女性の声を設定しており、男性より周波数の広がりはなく横縞のようになっている特徴がうかがえる。
上図3番目で両音が混ざり合った様子が見え、上図一番下の分離後音声を見ると女性の声で特徴的だった横縞のスペクトログラムの特徴が抑えられていることが分かる。遅延和法ではマイクロホンアレイを32個使用したが、最小分散法ではマイクロホンアレイを2個しか使用していないが、同等の音源分離性能を実現できていることが分かる。