本記事について
本記事は音響工学に関する以下参照書籍について勉強中のなか、自身の理解の定着のために記したものです。シミュレーションプログラムは参考書籍同等の部分については記載を省略しているため、本記事掲載部分のみでは動作しない場合があります。技術内容については参考書籍その他書籍やネット検索等々で調べておりますが、それを誤った解釈をして記載している可能性がありますのでご注意ください。(指摘頂けると助かります。)
参考書籍
戸上真人.「Pythonで学ぶ音源分離」インプレス.2020年
遅延和ビームフォーミング定性的理解
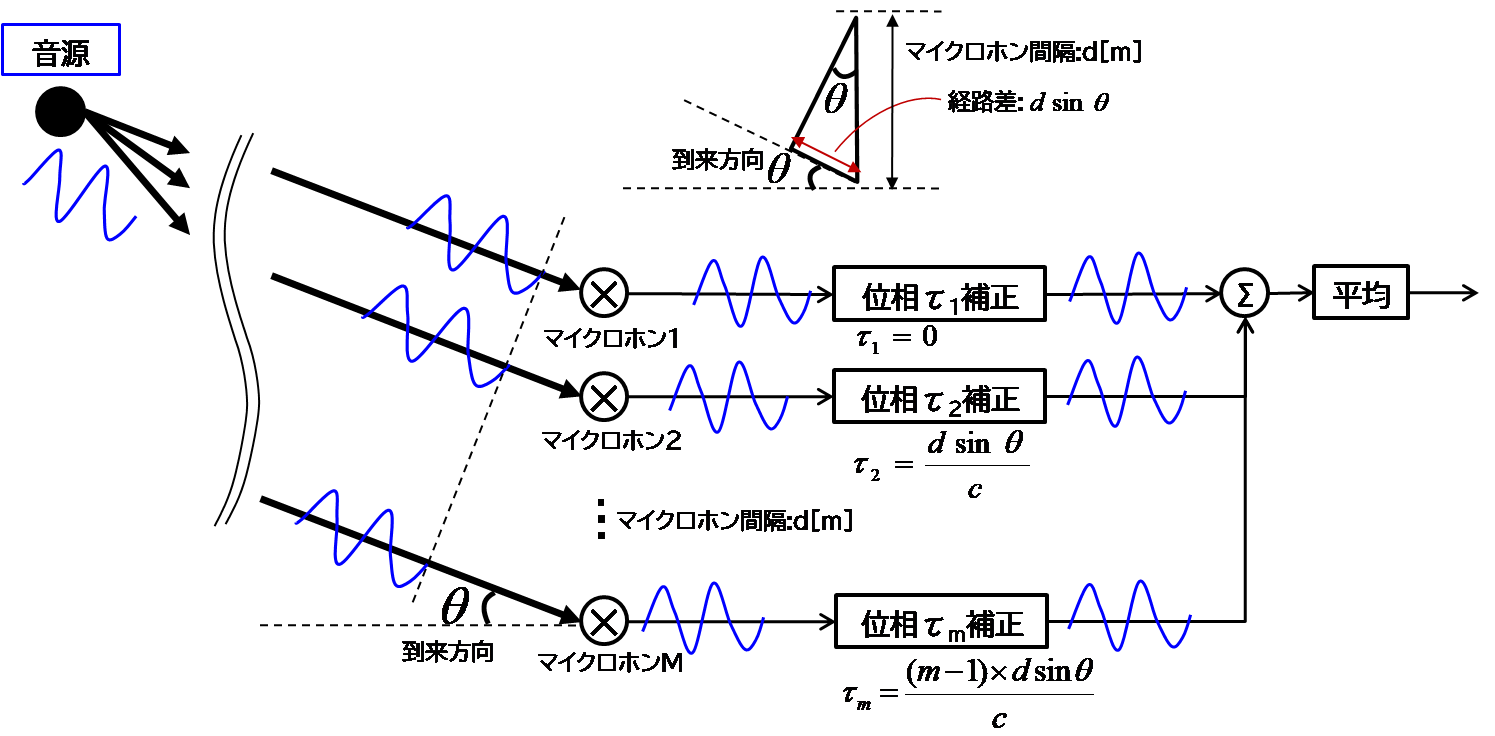
遅延和ビームフォーミングは、到来方向$\theta$でやってくる所望の音源信号のみ強調するようにマイクロホンアレイそれぞれのマイクの到来時間差$\tau$に応じて位相補正する。到来方向$\theta$でやってくる音源信号の位相が合うようにすれば、到来方向$\theta$以外の干渉信号は各マイクロホン間で振幅の正負のズレにより平均を取った際に打ち消されるため、所望の音源信号のみが強調され取り出すことができる。
遅延和法のフィルタ係数
マイクロホンで受信した信号は、音源信号に対しステアリングベクトルを(音の空間伝搬モデルとみなした)伝達関数に通した信号とみることができる。上記定性的理解のように、音源信号の到来時間差(伝達関数でいうと位相差)を補正するフィルタ係数とすればよいが、音源分離時はフィルタ係数の複素共役転置との内積で音源信号を推定するため、フィルタ係数はステアリングベクトルそのままとなる。
w(k) = a(k)
Pythonシミュレーション確認
問題設定
以下の縦横10mの2次元平面で考える。部屋中央にマイクロホンをy方向に32個配置し、x軸方向から反時計回りに20度の方向から目的音を設置し、x軸方向から時計回りに80度の方向(反時計回りに-80度の方向)に干渉音を設置した。
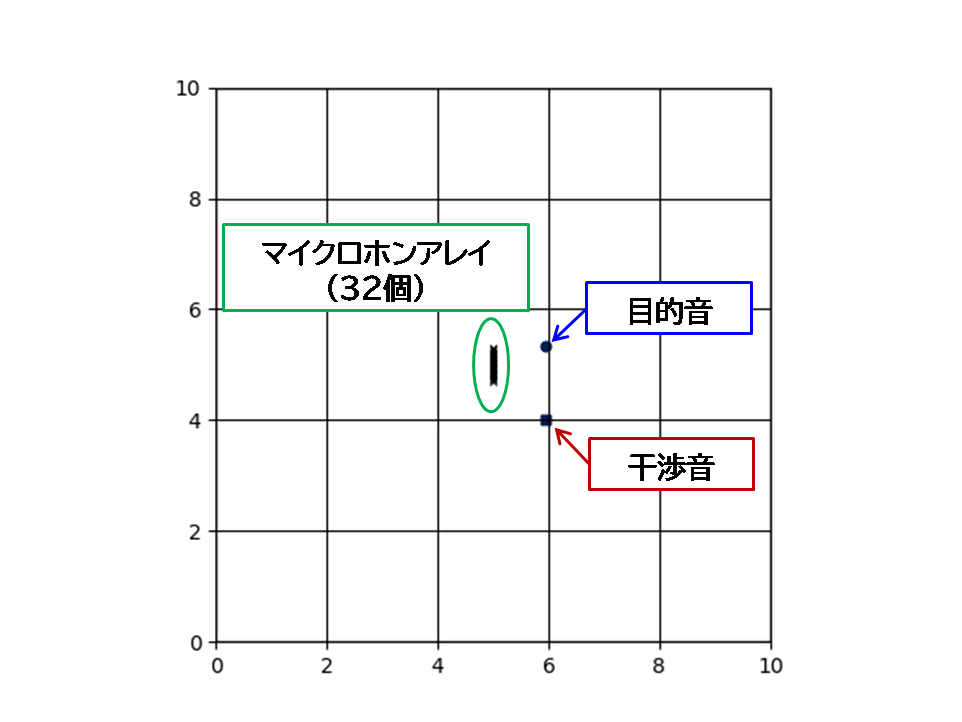
シミュレーションは、Pythonのpyroomacousticsモジュールを使用したシミュレーション環境を用いる。設定の仕方の詳細は参考書籍に譲るが、今回は以下のように設定を行った。(プログラム一部抜粋して表示)
import pyroomacoustics as pra
# 部屋を生成する
room_dim = np.r_[10.0, 10.0]
room = pra.ShoeBox(room_dim, fs=sample_rate, max_order=0)
# 部屋にマイクを配置
mic_array_loc = room_dim / 2
mic_alignments = np.array([[0.0, y] for y in np.arange(-0.31, 0.32, 0.02)])
R = mic_alignments.T + mic_array_loc[:, None] # マイクロホンアレイの座標
mics = pra.Beamformer(R, fs=room.fs) # ビームフォーマオブジェクトオブジェクト生成
room.add_microphone_array(mics) # 部屋にマイクロホンアレイ情報を設定
# 部屋に音源を配置
theta = [20.0, -80.0] # 到来方向[deg] 0:目的音, 1:干渉音
rad = np.array(theta)*2.0*np.pi/360
source_locations = np.zeros((n_sources, rad.shape[0]), dtype=rad.dtype)
source_locations[0, :] = np.cos(rad[0])
source_locations[1, :] = np.sin(rad)
source_locations += mic_array_loc[:, None]
for s in range(n_sources):
clean_data[s] /= np.std(clean_data[s])
room.add_source(source_locations[:, s], signal=clean_data[s])
pyroomacousticsにはビームフォーミング手法がいくつか実装されており、今回は参考書籍記載の遅延和法とpyroomacoustics.beamforming に実装されている遅延和法の比較を行ってみるため、Beamformerオブジェクトを生成している。
clean_dataの読み込み方法は参考書籍を参考にされたい。今回は参考書籍で使用している2音源をそのまま使用し、目的音を男性の声、干渉音を女性の声とした。
ビームフォーミング(遅延和法)の指向特性の表示
pyroomacoustics.beamforming に実装されている遅延和法のビームフォーミング指向特性を表示してみる。pyroomacousticsでは、Beamformerオブジェクトからフィルタ係数生成し、plotにて表示できる。遅延和法のフィルタ係数生成は、rake_delay_and_sum_weights にて実施される。以下のy1,y2は、目的音や干渉音との到来方向の補助線を点線として表示した。
mics.rake_delay_and_sum_weights(room.sources[0][:1])
fig, ax = room.plot(freq=[2000, 3000, 4000, 5000, 6000], img_order=0)
x = np.arange(5, 11, 1)
y1 = (source_locations[1, 0]-5.0)/(source_locations[0, 0]-5.0)*(x-5.0)+5.0
y2 = (source_locations[1, 1]-5.0)/(source_locations[0, 1]-5.0)*(x-5.0)+5.0
plt.plot(x, y1, color='k', ls="--", lw=0.5)
plt.plot(x, y2, color='k', ls="--", lw=0.5)
plt.grid()
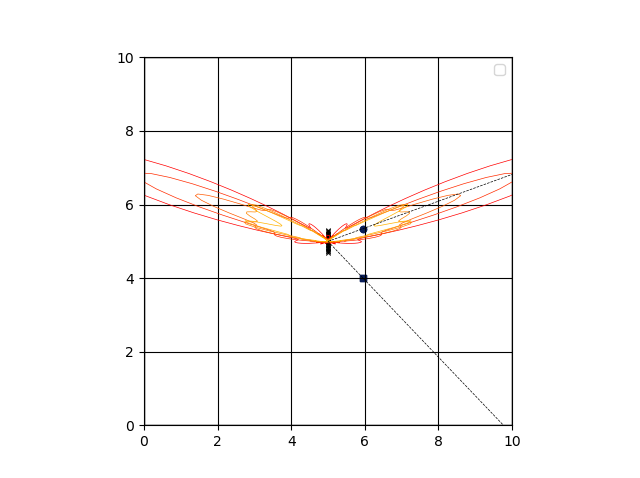
少し拡大する。
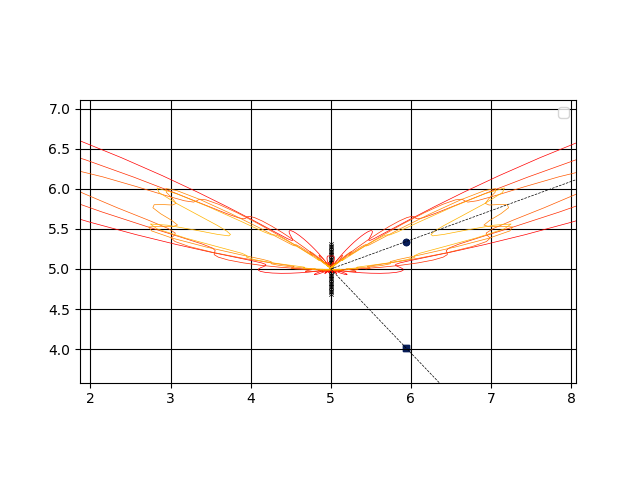
目的音に対して指向性が向いていることと、干渉音に対しては抑制するようにビームを形成できていることが確認できる。
書籍計算とpyroomacousticsのビームフォーミング指向特性比較
ビームフォーミングの指向特性を表示してみると以下のようになった。まずは、参考書籍記載のフィルタ計算式から算出した指向特性は以下のようになった。表示プログラムは参考書籍記載通りである。
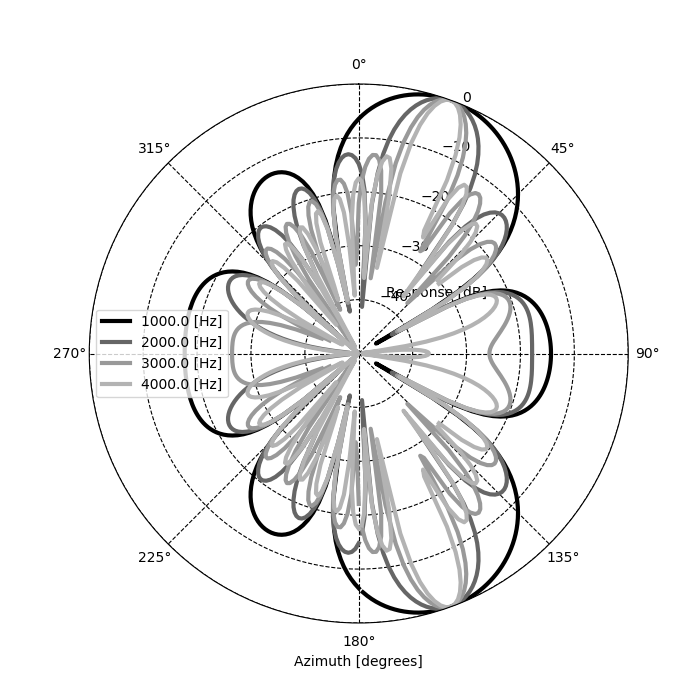
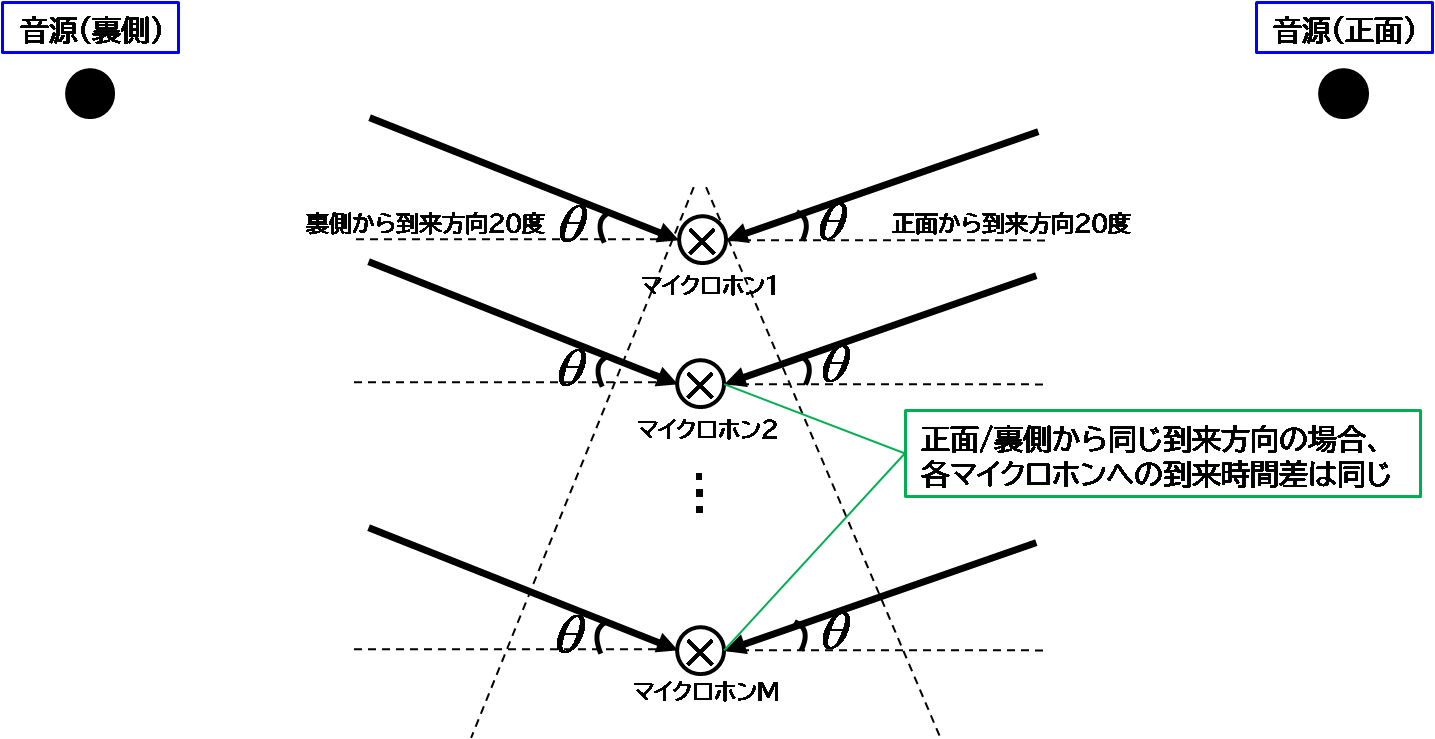
目的音である到来方向20度に指向性が向いており、その他の角度はゲインを抑制していることがわかる。ただし、到来方向160度についての指向性も現れてしまっていることがわかる。本ビームフォーミングはマイクロホン間の到来時間差情報が肝となるのだが、マイクロホンアレイに対して正面からくる20度と、裏側からくる20度(正面から160度)は同じ到来時間差となるため、正面から来ているか裏側から来ているかを区別できないということを示している。(上図、xy座標上に表示した指向特性が左右に広がっていることからもイメージしやすい。)
続いて、pyroomacousticsに実装されている遅延和法ビームフォーミングの指向性は以下のようになった。
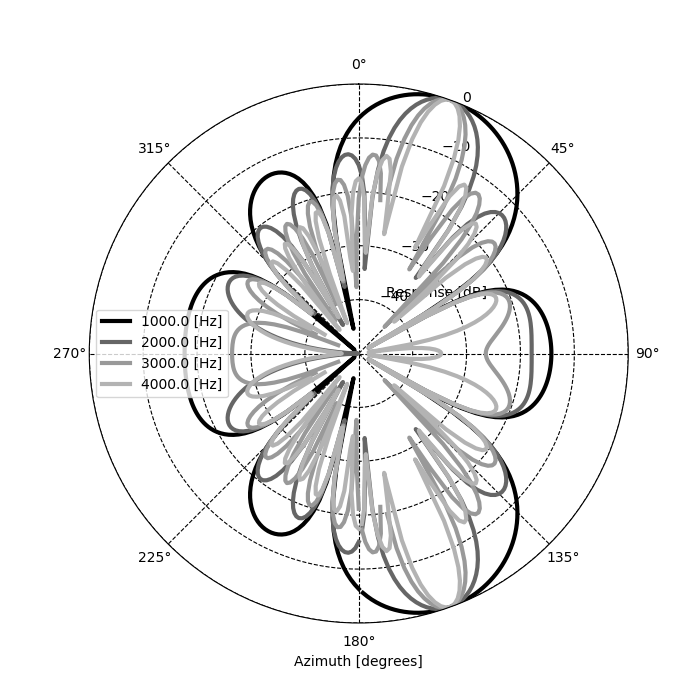
pyroomacousticsに実装されている遅延和法ビームフォーミングのフィルタ係数は、Beamformerクラスから生成したインスタンス mics のメソッド weights で取り出すことができる。以下に、pyroomacousticsに実装されている遅延和法ビームフォーミングの指向性計算部分を抜粋掲載する。mics.weights で取り出した配列形式(マイク数×周波数ビン数)となっているため、書籍計算に合うように転置して使用している。
取り出した係数をそのまま計算に使用せずコメントアウトしている「W_dsbf = wm.T」点については後述する。
chk_rad = np.array(
[theta for theta in np.arange(-np.pi, np.pi, 2.0*np.pi/360.0)]
)
source_locations = np.zeros((2, chk_rad.shape[0]), dtype=chk_rad.dtype)
source_locations[0, :] = np.cos(chk_rad)
source_locations[1, :] = np.sin(chk_rad)
chk_steering_vectors = calculate_steering_vector(mic_alignments.T,
source_locations,
freqs,
is_use_far=False)
wm = mics.weights
#W_dsbf = wm.T
W_dsbf = wm.T * np.abs(W_dsbf_alg[0, 0])/np.abs(wm[0, 0])
val = np.einsum("km, ksm->ks",
np.conjugate(W_dsbf),
chk_steering_vectors)
beam_pattern = np.square(np.abs(val))
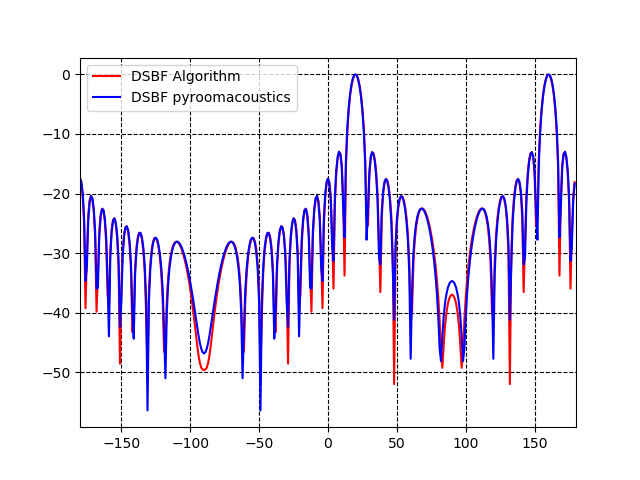
周波数4000Hzを取り出して比較表示する。凡例の「DSBF Algorith」は書籍計算式で算出した線である。概ね指向特性は一致している。
指向特性比較時の注意点
ここで、上記「#W_dsbf = wm.T」をコメントアウトしていた点についての解釈を説明する。まず、マイクロホンアレイ1(y軸方向で一番上のマイク)のフィルタ係数について、書籍計算とpyroomacoustics算出の係数wmをそのまま比較表示すると以下のようであった。上側が振幅特性、下側が位相特性である。
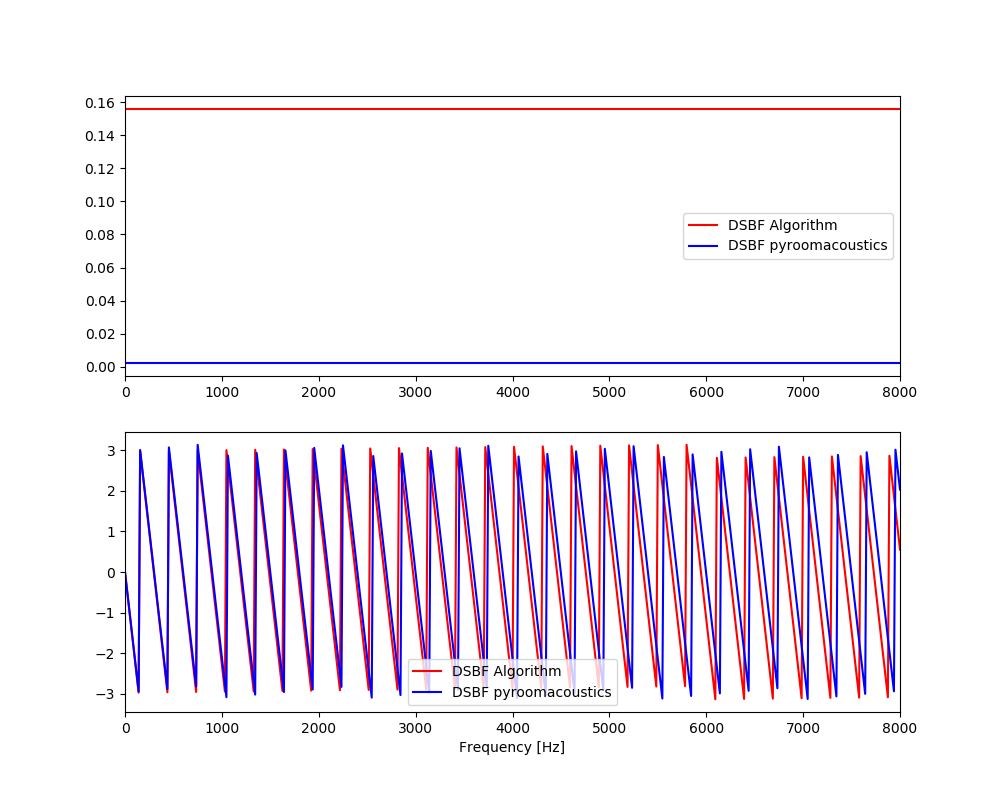
遅延和法によるビームフォーミングは到来時間差情報を肝としているため、振幅特性は一定であり、位相特性のみ変化する点については定性的理解と一致し、位相特性は概ね一致している。ただし、振幅値については値が異なっている。
遅延和法によるビームフォーミングのフィルタ係数はステアリングベクトルとなるが、ステアリングベクトルのゲイン値の計算は、参考書籍ではステアリングベクトルの$L_2$ノルムが1となるような値としている。
一方、pyroomacousticsのフィルタ計算は、音源放射特性(減衰は距離の2乗に比例)を加味したゲイン値が計算されている可能性がある。(結論付けるためにはpyroomacousticsの詳細仕様をより調べる必要がある。)
参考書籍の指向特性の計算では、角度捜査用ステアリングベクトルchk_steering_vectorsも$L_2$ノルムを1としたゲイン値のステアリングベクトルとして内積を計算し、ビームフォーミング方向と一致した角度での内積値が1(0dB)となるように評価しているため、
上記ゲイン値違いの前提があることを考慮し、pyroomacousticsのステアリングベクトルゲイン値を書籍計算のステアリングベクトルゲイン値に換算して指向特性を計算した。
wm = mics.weights
#W_dsbf = wm.T
W_dsbf = wm.T * np.abs(W_dsbf_alg[0, 0])/np.abs(wm[0, 0])
スペクトログラムによる音源分離性能の確認
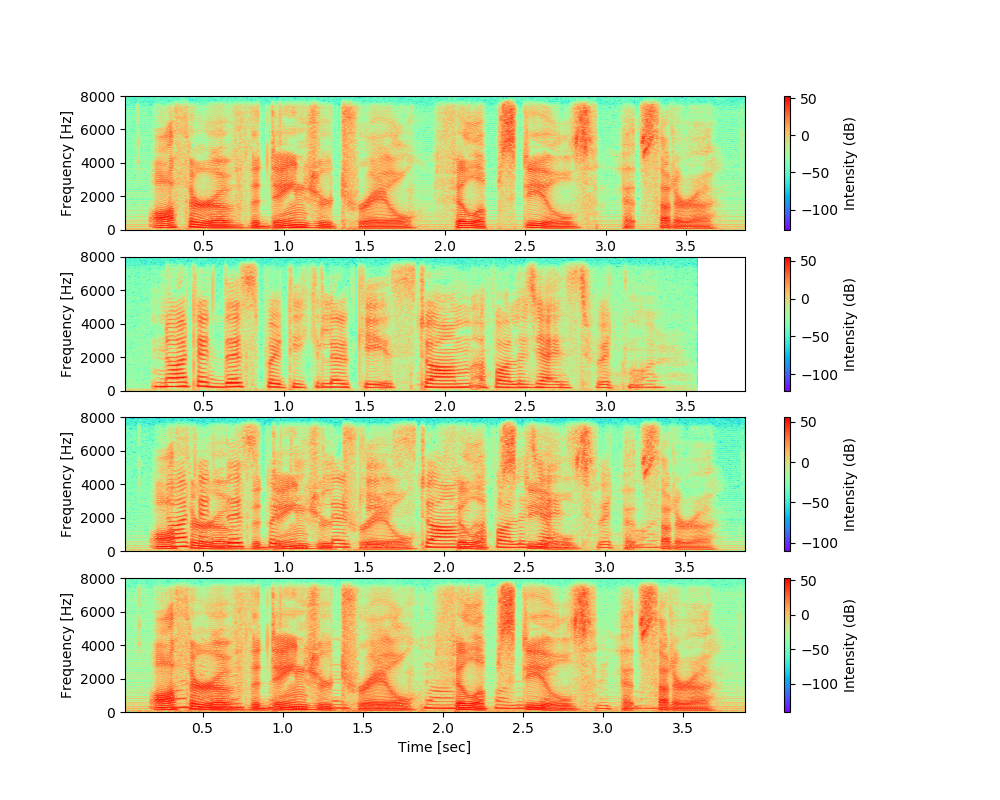
遅延和法によるビームフォーミングを用いた音源分離性能を確認した。以下図は上から目的音、干渉音、マイクロホンでの計測音(目的音と干渉音の合算)、ビームフォーミングによる分離音を示している。一番下のスペクトログラムが一番上のスペクトログラムに近ければ分離性能が良い。
今回、目的音は男性の声で主に低周波数を中心として周波数に多少広がりを持っている特徴となっている。干渉音として女性の声を設定しており、男性より周波数の広がりはなく横縞のようになっている特徴がうかがえる。上図3番目で両音が混ざり合った様子が見え、上図一番下の分離後音声を見ると女性の声で特徴的だった横縞のスペクトログラムの特徴が抑えられていることが分かるが、低周波数域での分離性能がいまいちであり、分離後音声を聞いてみるとかすかに女性の声が聞こえる。遅延和法によるビームフォーミングは目的の到来方向外の信号については到来時間差による平均化で打ち消そうとしているが、低周波数では波長が長くなるためマイクロホン間で波の正負で打ち消すことができる位相差を十分に取りづらいのかもしれない。