はじめに
背景
川に笹舟を流し速さを競い合う遊びは多くの人が遊んだことのある定番の川遊びである.
しかし笹舟の形状がどうあるべきかについての考察は多くない.
川遊びで子供を圧倒するためにも, まずは二重楕円状の水路(以下FNM)を浮遊する物体の挙動の予測を行う
提案方法
本来浮遊する物体の挙動を予測するためには,流れ場と舟の挙動を連成して解析すべきである.
しかし舟の形状を検討するためには多数の計算が必要となるため計算時間を短くする必要がある.
そこで今回,槽内に物体を浮遊させない状態のFNM単体の槽内流れ解析と,
その解析結果(流れ場)から物体が受ける力を推定し挙動を予測する方法を提案する.
Flowing Noodle Machine
FNMは,2基ある渦巻きポンプの駆動モータの電源を電池→家庭用電源に,
さらに電圧制御と回転数を計測できるように改造された上,
可視化のため流路内壁を黒く塗装されてしまった流しそうめん機である.
Flowing Noodle Machine for Qiita pic.twitter.com/lobq32zF1v
— 片山達也 (@TatsuyaKatayama) 2016年11月23日
実測実験
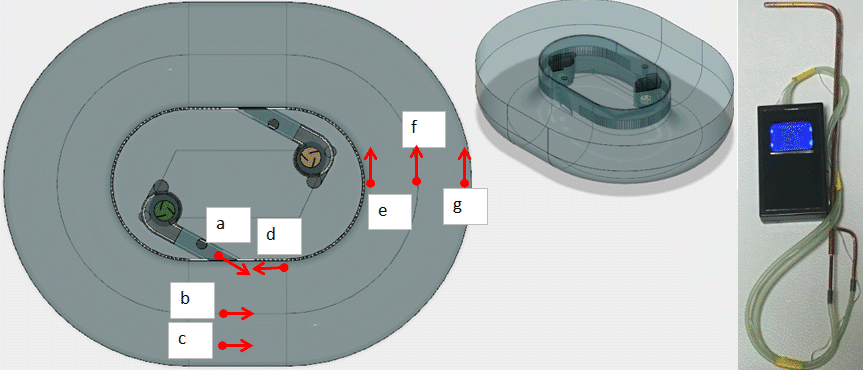
FNM槽内の流れ場を把握するため水の流速を手作りのピトー管で流速を計測した.計測に用いたピトー管,計測ポイント,計測結果(流速)を示す。
| a | b | c | d | e | f | g |
|---|---|---|---|---|---|---|
| 1.09 [m/s] | 0.47 [m/s] | 0.47 [m/s] | 0.47 [m/s] | 0.33 [m/s] | 0.47 [m/s] | 0.47 [m/s] |
FNM槽内流れ解析
解析実行
FNM槽内は水の自由表面流れである。
これをOpenFOAM(R)のVOF法ベースの混相流ソルバーであるinterFoamを用いて計算する.
git clone https://github.com/OpenCAE-Local-User-Group-at-Kansai/OpenFOAM_Sample_Cases.git
cd OpenFOAM_Sample_Cases/Experiment-Using-Flowing-Noodle-Machine/OpenFoam_CaseFile/\
Full_model/rev.1\(move\ two\ pump\)/
tar -xf flowing-noodle-MRF.tar.bz2
cd flowing-noodle-MRF
本解析はOpenFOAM-2.3.xを用いており、バージョンの違う環境で計算を行う場合、
各設定ファイルの書き換えが必要となる.
Allrunファイル内3行目のOpenFOAMのパスを環境に合わせて変更する.
./Allrunを実行すれば計算が始まる.
MPI並列計算に対応しており8並列で約2週間計算すれば,5秒分の計算が完了する.(デフォルトは2並列.)
# !/bin/sh
# edit path to OpenFOAM
. /Volumes/OpenFOAM/OpenFOAM-2.3.x/etc/bashrc
# cd ${0%/*} || exit 1 # run from this directory
# Source tutorial run functions
. $WM_PROJECT_DIR/bin/tools/RunFunctions
# - meshing
runApplication blockMesh
runApplication surfaceFeatureExtract
cp system/decomposeParDict.h system/decomposeParDict
runApplication decomposePar
mkdir 0
runParallel snappyHexMesh 2
# - reconstruct mesh
runApplication reconstructParMesh -latestTime
cp -r 0.0002/polyMesh/* constant/polyMesh
rm -fR 0.0002
# force removal of fields generated by snappy
\rm -rf 0
# - test by running moveDynamicMes
# runApplication moveDynamicMesh -checkAMI
# - set the initial fields
cp -rf 0.org 0
runApplication setSet -batch createWallAndImpeller.setSet
runApplication createPatch -overwrite
runApplication setFields
runApplication transformPoints -scale '(0.001 0.001 0.001)'
runApplication renumberMesh -overwrite
# decompose case
rm log.decomposePar
cp system/decomposeParDict.p system/decomposeParDict
# run solver
rm -fR processor*
runApplication decomposePar
sleep 2
runParallel interFoam 2
最後のrunParallel interFoam 2を下の2行のように変更すれば、8並列で計算が始まる.
sed -i 's/numberOfSubdomains 2;/numberOfSubdomains 8;/' system/decomposeParDict
runParallel interFoam 8
解析結果
結果のアニメーションを示す.
Flow In FNM for Qiita pic.twitter.com/TaJkVjnwi2
— 片山達也 (@TatsuyaKatayama) 2016年11月23日
実測-解析の結果比較
致命的なことに,実測と解析で駆動モータの回転数が揃っていない.(実験の方が回転数が低い)
今回2種類の回転数で流速計測を行っており,渦巻きポンプの流量は回転数比$\frac{N_1}{N_2}$に比例するとして
流入部の流速である計測点aの流速を外挿し比較する.
CFDの結果はOpenFOAMで計算したもので4~5[s] 平均の流速である.
| point | experiment | CFD |
|---|---|---|
| a | 1.47 [m/s] | 0.84~1.21 [m/s] |
流速は解析の方が遅く,MRFモデルによる流量の過小評価,計算結果の未収束が考えられる.
約1.5倍流速がでていないが,今回はこのまま押し進める.
浮遊する物体の運動
基礎方程式
速度$\boldsymbol v_L$、回転各速度$\boldsymbol \omega_L$の流れ場の中を、
質量$m$、慣性モーメント$\boldsymbol I$の物体が、速度$\boldsymbol v$、角速度$\boldsymbol \omega $で運動している場合を考える。
重力ベクトル$\boldsymbol g = (0,0,g)$で、浮力による力とモーメントを$\boldsymbol f_B, \boldsymbol T_B$とし、
流体から受ける力とモーメントを$\boldsymbol f_F ,\boldsymbol T_F $とし、
物体がコース壁に接触し受ける力とモーメントを$\boldsymbol f_W,\boldsymbol T_W$とした場合、__前置き文は複雑化し呪文__になる。
一方、物体の運動方程式は次のようになる
\begin{eqnarray}
m\frac{d\boldsymbol v}{dt} & = & \boldsymbol f_F + \boldsymbol f_W + \boldsymbol f_B -m \boldsymbol g\\
{\boldsymbol I}\frac{d\boldsymbol w}{dt} & = & \boldsymbol T_F + \boldsymbol T_B + \boldsymbol T_W
\end{eqnarray}
ここで$\boldsymbol f_F $ は物体と流れ場の速度差$\boldsymbol v - \boldsymbol v_L$によって生じ、
$\boldsymbol T_F $は物体と流れ場の角速度差$\boldsymbol v - \boldsymbol v_L$によって生じる。
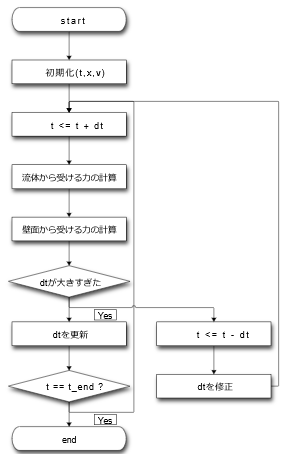
解法
運動方程式の微分方程式は,壁面接触があるためスティフな式となる.そのため,時間積分のタイムステップには注意が必要であるそこで数値積分にはPythonのパッケージであるassimuloを利用する.
assimuloは1DCAEのオープンソースソフトでも知られるJModelic.orgの内部でも利用されており,不連続な関数の積分や代数微分方程式に有用な積分方法を含むフレームワークである.
今回,マルチステップで後退微分方程式として解く方法を採用する.
流体から受ける力の推定
今回,任意位置の球体がFNM槽内の流体から受ける力の推定に用いた方法を下記に概説する.
- OpenFOAMのユーティリティであるmapFieldsを用い球体近傍のメッシュにFNM槽内流れ場をマッピングする.
- PyFoamを使い球体近傍の流れ場をPythonで読み込む.
- 流体の速度場からボールの速度を引く
- 3の速度場からボールに作用しているだろう動圧を計算する
- 計算した動圧を球体壁に負荷させ,OpenFOAMの境界値として書き戻す
- OpenFOAMのユーティリティー(functionObject)にて球体に作用する力を算出する
以下が,実際のプログラムである.
from PyFoam.Basics.DataStructures import Vector
from PyFoam.Basics.DataStructures import Dimension
from PyFoam.Basics.DataStructures import Field
from PyFoam.Execution.BasicRunner import BasicRunner
from PyFoam.RunDictionary.SolutionDirectory import SolutionDirectory
from PyFoam.RunDictionary.ParsedParameterFile import ParsedParameterFile
from PyFoam.RunDictionary.TimelineDirectory import TimelineValue
import numpy as np
import shlex, shutil
import os
def calcFlowForce(bplist,bUlist):
bp = np.array(bplist[:3])
bU = np.array(bUlist)
ball0 = SolutionDirectory("./of/ball00a/")
pointsdict = ParsedParameterFile( \
ball0.polyMeshDir() + "/points.org",boundaryDict=True)
vst = np.array(pointsdict.content)
vst = vst + np.array(bp)
verticeslist = []
for v in vst:
verticeslist.append(str(tuple(v.tolist())).replace(",",""))
pointsdict.content=verticeslist
pointsdict.writeFileAs(ball0.polyMeshDir()+ "/points")
#init state
initDir = ball0.initialDir()
shutil.rmtree(initDir)
shutil.copytree( initDir + ".org", initDir)
# calc cellcenter
cellCenter = shlex.split(
'writeCellCentres -case %s' \
% ball0.name )
cCenterRunner = BasicRunner(cellCenter, silent=True)
cCenterRunner.start()
#mapFields
shutil.copy( \
ball0.systemDir() + "/mapFieldsDict.alpha", \
ball0.systemDir() + "/mapFieldsDict")
mapfields1 = shlex.split(
'mapFields ../FNM_MRF \
-sourceTime latestTime \
-case %s \
-fields "(p alpha.water U)" \
-subtract' \
% ball0.name )
mapfields1[7] = "'" + mapfields1[7] + "'"
m1Runner = BasicRunner(mapfields1, silent=True)
m1Runner.start()
ccx = ParsedParameterFile(ball0.initialDir() + "/ccx")
ccy = ParsedParameterFile(ball0.initialDir() + "/ccy")
ccz = ParsedParameterFile(ball0.initialDir() + "/ccz")
xyz = np.array([
ccx.content["internalField"],
ccy.content["internalField"],
ccz.content["internalField"],
]).T
p = ParsedParameterFile(ball0.initialDir() + "/p")
U = ParsedParameterFile(ball0.initialDir() + "/U")
alpha = ParsedParameterFile(ball0.initialDir() + "/alpha.water")
p_fw = np.array( \
p.content["boundaryField"]["fixedWalls"]["value"]) * -1.
U_fw = np.array( \
U.content["boundaryField"]["fixedWalls"]["value"]) * -1.
alpha_fw = np.array( \
alpha.content["boundaryField"]["fixedWalls"]["value"]) * -1.
p_in = np.array(p.content["internalField"]) * -1.
U_in = np.array(U.content["internalField"]) * -1.
alpha_in = np.array(alpha.content["internalField"]) * -1.
p_bw = np.array( \
p.content["boundaryField"]["boundaryWalls"]["value"]) * -1.
alpha_bw = np.array( \
alpha.content["boundaryField"]["boundaryWalls"]["value"]) * -1.
#U - U_ball
U_in = U_in - bU[:3]
U_fw = U_fw - bU[:3]
#U - rotate_ball_velo
#r_x = xyz[:,0] - bp[0]
#r_z = xyz[:,2] - bp[2]
#r_U = bU[3] * np.c_[- r_x, r_z]
#r_Ux = np.dot(r_U, np.array([[0],[1]]))
#r_Uz = np.dot(r_U, np.array([[1],[0]]))
#U_in[:,0] = U_in[:,0] - r_Ux[:,0]
#U_in[:,2] = U_in[:,2] - r_Uz[:,0]
bd = ParsedParameterFile(ball0.polyMeshDir() + \
"/boundary",boundaryDict=True)
points = ParsedParameterFile(ball0.polyMeshDir() + \
"/points",boundaryDict=True)
faces = ParsedParameterFile(ball0.polyMeshDir() + \
"/faces",boundaryDict=True)
fs = faces[ bd[1]["startFace"]: \
bd[1]["startFace"] + bd[1]["nFaces"]]
fc = np.zeros([len(fs),3])
for idx,f in enumerate(fs[:]):
fc[idx,:] = 0.25*np.array(points[f[0]]) + \
0.25*np.array(points[f[1]]) + \
0.25*np.array(points[f[2]]) + \
0.25*np.array(points[f[3]])
norm = -fc + bp
norm = norm / np.linalg.norm(norm,axis=1)[:,np.newaxis]
Un_fw = np.zeros(norm.shape[0])
for i in range(0,norm.shape[0]):
Un_fw[i] = np.dot(norm[i,:],U_fw[i,:])
bUn_fw = Un_fw > 0
trans = ParsedParameterFile(ball0.constantDir() + \
"/transportProperties")
rho_w = trans["water"]["rho"][-1]
rho_a = trans["air"]["rho"][-1]
pd_fw = (rho_w * alpha_bw + rho_a * (1. - alpha_bw)) \
* Un_fw * Un_fw * bUn_fw * 0.5
p_fw = p_fw + pd_fw
p.content["boundaryField"]["boundaryWalls"]["value"] = \
Field(p_bw.tolist(),"List<scalar>")
alpha.content["boundaryField"]["boundaryWalls"]["value"] = \
Field(alpha_bw.tolist(),"List<scalar>")
p.content["boundaryField"]["fixedWalls"]["value"] = \
Field(p_fw.tolist(),"List<scalar>")
U.content["boundaryField"]["fixedWalls"]["value"].setUniform( \
Vector(0,0,0))
alpha.content["boundaryField"]["fixedWalls"]["value"] = \
Field(alpha_fw.tolist(),"List<scalar>")
p.content["internalField"]=Field(p_in.tolist(),"List<scalar>")
U.content["internalField"]=Field(U_in.tolist(),"List<vector>")
alpha.content["internalField"]=Field(alpha_in.tolist(),"List<scalar>")
p.writeFile()
U.writeFile()
alpha.writeFile()
os.system("sed -i 's/^ 3//g' %s"% ball0.initialDir() + "/U" )
cntDict = ParsedParameterFile(ball0.controlDict())
cntDict.content["functions"]["forces"]["CofR"] = \
Vector(bp[0],bp[1],bp[2])
cntDict.writeFile()
createPhi = shlex.split(
'createPhi -case %s' \
% ball0.name )
cPhiRunner = BasicRunner(createPhi, silent=True)
cPhiRunner.start()
shutil.rmtree(ball0.name + "/postProcessing", ignore_errors=True)
execFuncObj = shlex.split(
'execFlowFunctionObjects -case %s' \
% ball0.name )
execFuncRunner = BasicRunner(execFuncObj, silent=True)
execFuncRunner.start()
tv = TimelineValue( \
ball0.name + "/postProcessing/forces/0", \
"forces.dat", 0)
Fflow=np.array(tv.getData([1])[0]).reshape(6,3)
flowF = np.sum(Fflow[:3,:],axis=0)
flowM = np.sum(Fflow[3:,:],axis=0)
return np.r_[flowF,flowM[1]]
if __name__ == "__main__":
bp = [ 0., -0.0285, 0.12,0.]
bU = [ 0., 0., 0.,0.]
print calcFlowForce(bp,bU)
壁面から受ける力の推定
壁面から受ける力はペナルティ法にて計算を行う.
球体とFNM内壁との接触はHertzの接触応力より算出している.
幾何形状のハードコーディングや,まとまりがないので後日差し替え予定.
import numpy as np
def calcWallForce(bplist,r_ball=0.01):
bp = np.array(bplist[:3])
if bp[0] > - 0.05 and bp[0] < 0.05:
if bp[2] > 0:
zone = 0
else:
zone = 2
else:
if bp[0] > 0:
zone =1
else:
zone = 3
if zone == 0:
l = bp[2]
ball2wall = np.array([
[l - r_ball - 0.08],
[0.19 - (l + r_ball)] ])
flg_contact = ball2wall < 0
norm = np.array([
[0, 0., 1.],
[0, 0., -1.]])
arm = r_ball * np.array([-1., 1.])
elif zone == 2:
l = -bp[2]
ball2wall = np.array([
[l - r_ball - 0.08],
[0.19 - (l + r_ball)] ])
flg_contact = ball2wall < 0
norm = np.array([
[0, 0.,-1.],
[0, 0., 1.]])
arm = r_ball * np.array([1., -1.])
elif zone == 1:
l = np.sqrt(np.power(bp[0]-0.05,2)+np.power(bp[2],2))
ball2wall = np.array([
[l - r_ball -0.08],
[0.19 - (l + r_ball)]])
flg_contact = ball2wall < 0
norm = np.array([
bp -np.array([0.05,bp[1],0]),
np.array([0.05,bp[1],0])-bp])
norm = norm / np.linalg.norm(norm,axis=1)[:,np.newaxis]
arm = r_ball * np.array([-1., 1.])
elif zone == 3:
l = np.sqrt(np.power(bp[0]+0.05,2)+np.power(bp[2],2))
ball2wall = np.array([
[l - r_ball -0.08],
[0.19 - (l + r_ball)]])
flg_contact = ball2wall < 0
norm = np.array([
bp -np.array([-0.05,bp[1],0]),
np.array([-0.05,bp[1],0])-bp])
norm = norm / np.linalg.norm(norm,axis=1)[:,np.newaxis]
arm = r_ball * np.array([-1., 1.])
E_ball = 1.e6 #[Pa]
v_ball = 0.45
mu = 0.35
K = 4./3. *np.sqrt(r_ball) * E_ball/(1.-v_ball**2)
Mw = np.dot(arm, mu*K * np.power(-ball2wall*flg_contact,1.5))
Fw = norm * K * np.power(-ball2wall*flg_contact,1.5)
Fw = np.dot(np.array([1.,1]), Fw)
return np.r_[Fw,Mw]
if __name__ == "__main__":
bp = [ 0.0501, -0.02694398, 0.089808385815, -1.32903042]
r_ball = 0.01
print calcWallForce(bp,r_ball)
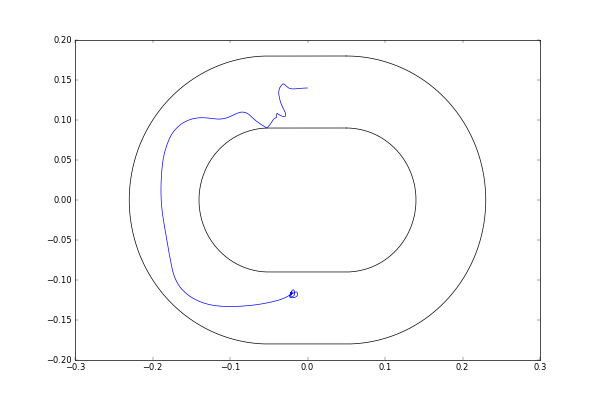
解析結果
渦にはまる・・・
再トライ
- なめらかでない挙動?球体の慣性が小さい? => 慣性力のチェック・・・間違いなし
- 初期位置で不思議な動き(球体の速度と流体の速度の差異の大きい部分で不思議挙動)=> 球体壁面に作用する動圧の算出の見直し
Un_fw = np.zeros(norm.shape[0])
for i in range(0,norm.shape[0]):
Un_fw[i] = np.dot(norm[i,:],U_fw[i,:])
bUn_fw = Un_fw > 0
Un_fw = np.zeros(norm.shape[0])
for i in range(0,norm.shape[0]):
Un_fw[i] = np.dot(norm[i,:],U_fw[i,:])
bUn_fw = Un_fw > 0
bUn_fw = (bUn_fw - 0.5) * 2.0
- そもそも流速が実測計測より遅い。=> えいやぁと言いながらFNM槽内流れ場 x 1.5倍
解析結果(再トライ)
吹き飛ばされる
とは言え、未解決であった慣性が小さく見える現象はなくなった.逆に慣性が大きすぎるようにも見える
おわりに
まとめ
- FNMの槽内流れの実測実験を行った
- 実験とは違う回転数でCFDを行った
- FNM内を浮遊する球体の挙動予測を行った
- 計算によると球体は渦にはまり吹き飛ばされた
今後
- FNM槽内流れ解析の精度向上が必要
- 球体に作用する動圧の算出方法を見直す
- 計算した結果を実測結果と比較する
- ソースコードはもう少し体裁を整えてGitHubに公開する
- 上記の取組みをオープンCAE勉強会@関西で継続する?
謝辞
本発表は,流しそうめん機を自発的に改造を施された人,無料枠を越してまでHPCサーバで計算してくれた人,勉強会に毎回FNMをハンドキャリーしてくれた人,CADデータを作成してくれた人,興味があるかわからないが実験に付き合ってくれた人など,オープンCAE勉強会@関西に関与いただいた様々な人達に支えられています。この場を借りてこの場をかりて御礼申し上げます